-
In order to ensure the secure and effective transmission of image information, a new method of optical image encryption using the multimode fiber (MMF) specklegram based compressive sensing combined with the double random phase encoding (DRPE) is proposed in this paper. The specklegrams obtained from the facet of the multimode fiber are used as the measurement matrix of compressive sensing (CS), and the compression and the first-stage encryption of the image are completed by compressive sensing, in which the specklegram also functions as the first secret key. Then, the second-stage encryption is implemented by using the double random phase encoding technology, in which the random phase mask acts as the second secret key. All of the specklegrams used in this paper are obtained from the facet of a 5 m-long and 105-μm-diameter-MMF and offset launching technique. Then the fiber specklegrams are proposed in several steps to provide the measurement matrix in CS. By performing an encryption and decryption test on a standard Lena image of 256 × 256 size, it is found that the decrypted image and the original image are visually consistent, and the encryption is also realized in the process of compression, which indicates the method proposed in this paper is feasible. Furthermore, the comparison studies of the performances of specklegram based measurement matrix and some classic measurement matrices show that the decrypted image quality using the specklegram matrix is better. And at the same time, comparing with the high hardware implementation complexity and high cost of other measurement matrices, specklegram based matrix can be easily realized by simple optical device, and the corresponding secret key can be easily changed by the working wavelength, which is helpful for enlarging the secret key space. It is further proved that the encryption method be able to effectively resist the statistical analysis attacks, cropping attacks and noise interference, and also have high sensitivity to the secret key, which shows good robustness and high security. Therefore, the image encryption method combined with the specklegram matrix based compression sensing with the optical DRPE can obtain good encryption effect and has a great secret key space, which may provide a good candidate scheme for the pure optical realization of image encryption.
-
Keywords:
- multimode fiber specklegram /
- compressive sensing /
- optical image encryption /
- double random phase encoding
[1] Javidi B 2005 Optical and Digital Techniques for Information Security (New York: Springer Business Media) pp36–40
[2] Refregier P, Javidi B 1995 Opt. Lett. 20 767
Google Scholar
[3] Javidi B 1997 Phys. Today 50 27
Google Scholar
[4] Unnikrishnan G, Joseph J, Singh K 2000 Opt. Lett. 25 887
Google Scholar
[5] Zhu B, Liu S, Ran Q 2000 Opt. Lett. 25 1159
Google Scholar
[6] Situ G H, Zhang J J 2004 Opt. Lett. 29 1584
[7] Chen L F, Zhao D M 2005 Opt. Commun. 254 361
Google Scholar
[8] Peng X, Zhang P, Wei H, Yu B 2006 Opt. Lett. 31 1044
Google Scholar
[9] Guo C, Liu S, Sheridan J T 2015 Appl. Opt. 54 4709
Google Scholar
[10] Li G W, Yang W Q, Li D Y, Situ G H 2017 Opt. Express 25 8690
Google Scholar
[11] Candes E, Romberg J, Tao T 2006 Commun. Pur. Appl. Math. 59 1207
Google Scholar
[12] Donoho D L 2006 IEEE Trans. Inform. Theory 52 1289
Google Scholar
[13] 肖迪, 谢沂均 2013 62 240508
Google Scholar
Xiao D, Xie Y J 2013 Acta Phys. Sin. 62 240508
Google Scholar
[14] 杨华千, 廖晓峰, Kwok-Wo Wong, 张伟, 韦鹏程 2012 61 040505
Google Scholar
Yang H Q, Liao X F, Kwok W W, Zhang W, Wang P C 2012 Acta Phys. Sin. 61 040505
Google Scholar
[15] Deepan B, Quan C, Wang Y, Tay C J 2014 Appl. Opt. 53 4539
Google Scholar
[16] Rawat N, Kim B, Muniraj I, Situ G, Lee B G 2015 Appl. Opt. 54 1782
Google Scholar
[17] Zhou N R, Li H L, Wang D, Pan S M, Zhou Z H 2015 Opt. Commun. 343 10
Google Scholar
[18] Lu P, Xu Z Y, Lu X, Liu X Y 2013 Optik 124 2514
Google Scholar
[19] Liu X Y, Cao Y P, Lu P, Li Y 2013 Optik 124 6590
Google Scholar
[20] Zhou N R, Zhang A D, Zheng F, Gong L H 2014 Opt. Laser Technol. 62 152
[21] Liu H, Xiao D, Liu Y B, Zhang Y S 2015 Optik 126 2663
Google Scholar
[22] Candès E J, Wakin M B 2008 IEEE Signal Proc. Mag. 25 21
Google Scholar
[23] Amphawan A, Payne F, O'Brien D, Shah N 2010 J. Lightwave Technol. 28 861
Google Scholar
-
图 1 多模光斑产生装置(LD, 半导体波长可调激光器; SMF, 单模光纤; MMF, 直径为105 μm的多模光纤, 长度为5 m; IR, 近红外相机)
Figure 1. Multimode specklegram generator (LD, laser diode; SMF, single mode fiber; MMF, multimode fiber; IR, infrared camera).
图 2 光斑矩阵构造流程示意图
Figure 2. Flow chart of the construction method of the fiber specklegram based measurement matrix.
图 3 基于4f的光学DRPE系统
Figure 3. Optical DRPE system based on 4f.
图 4 基于多模光纤散斑的压缩感知光学图像加密解密过程流程图
Figure 4. Flow chart of compressive sensing optical image encryption and decryption based on multimode fiber specklegram.
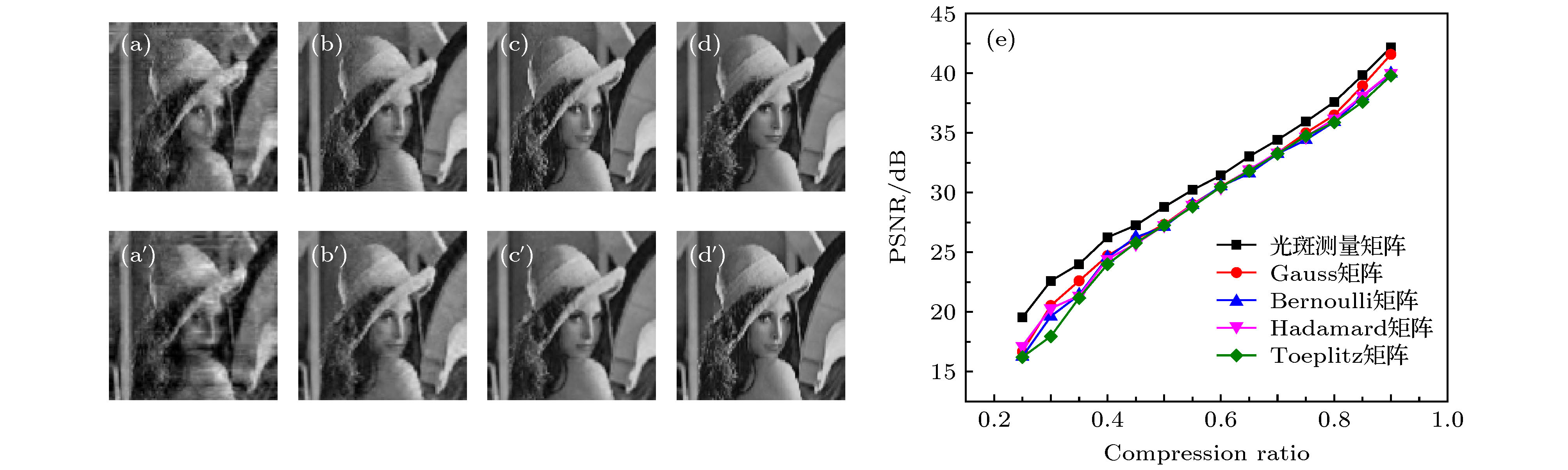
图 5 光斑矩阵和高斯矩阵对比分析 (a)−(d)使用光斑矩阵在压缩比为0.3, 0.5, 0.7, 0.9时的解密图像; (a')−(d')使用高斯矩阵在压缩比为0.3, 0.5, 0.7, 0.9时的解密图像; (e)使用不同测量矩阵时对应解密图像的PSNR随压缩比的变化
Figure 5. Comparative analysis of specklegram matrix and Gaussian matrix: (a)−(d) The decrypted image using specklegram matrix at compression ratio of 0.3, 0.5, 0.7, 0.9; (a')−(d') the decrypted image using Gaussian matrix at compression ratio of 0.3, 0.5, 0.7, 0.9; (e) comparison between the PSNRs of the decrypted images varying with the compression ratio when using different measurement matrices.
图 6 直方图分析 (a)原始图像; (b)原始图像对应的直方图; (c)密文的相位直方图; (d)密文的幅值直方图
Figure 6. Histogram analysis: (a) Original image; (b) histogram corresponding to original image; (c) phase histogram of ciphertext; (d) amplitude histogram of ciphertext.
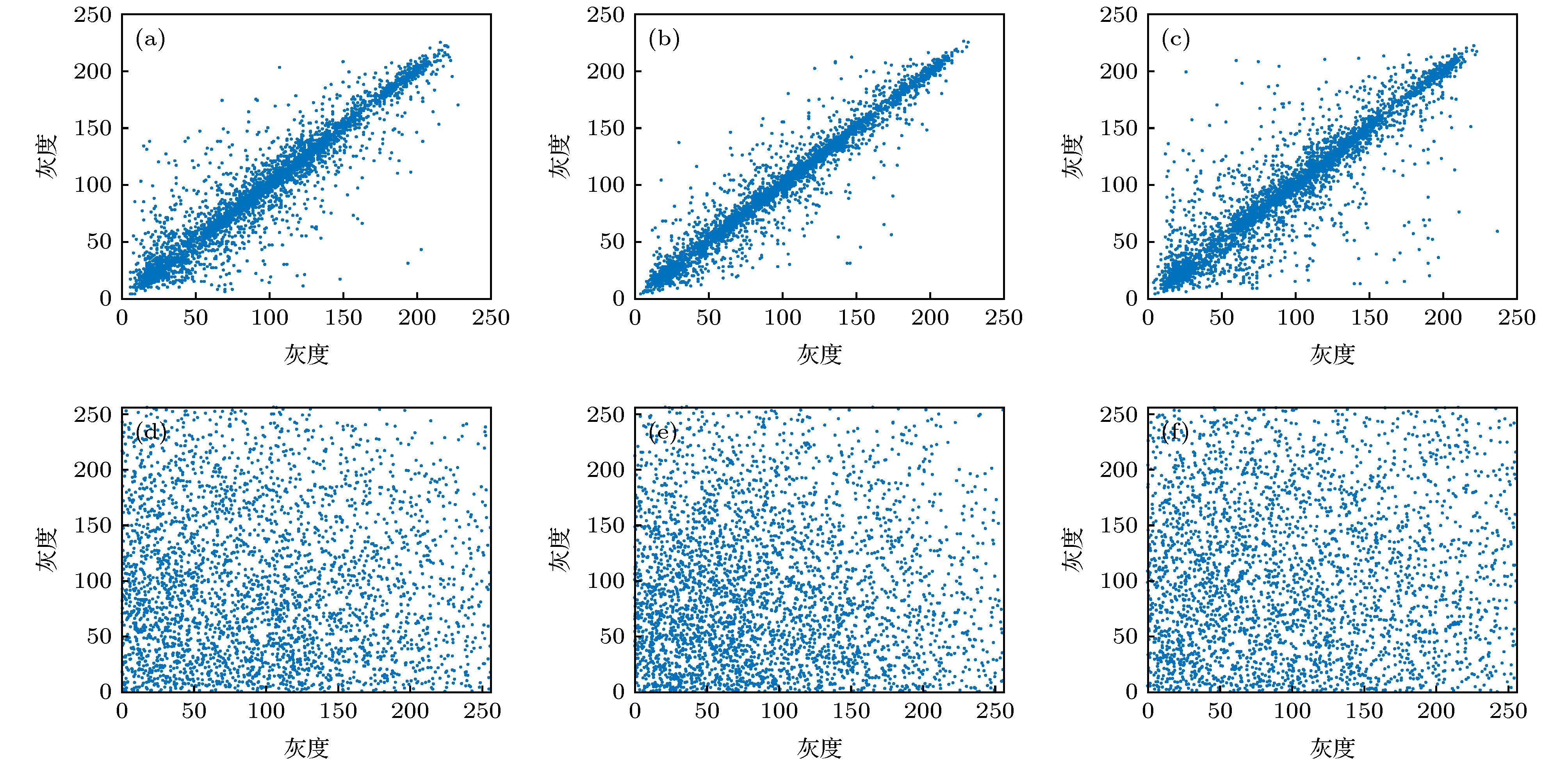
图 7 相关性分析 (a)−(c)分别为明文图像在水平、垂直和对角方向上的像素相关性分布; (d)−(f)分别为密文图像在水平、垂直和对角方向上的像素相关性分布
Figure 7. Correlation analysis: (a)−(c) Pixel correlation distributions of plaintext images in horizontal, vertical and diagonal directions; (d)−(f) pixel correlation distributions of ciphertext images in horizontal, vertical and diagonal directions.
图 8 抗噪声分析 (a)−(d)在密文图像中分别加入方差为0, 0.1, 0.3和0.5的噪声时的解密图像; (e)密文图像中加入噪声后的解密图像PSNR随相应噪声方差的变化
Figure 8. Anti-noise analysis: (a)−(d) Decrypted images with noise of 0, 0.1, 0.3 and 0.5 variances added to ciphertext image respectively; (e) curves of relationship between noise variance and the PSNR of decrypted image with noise in ciphertext mage
图 9 水平、垂直、中心和边角方向不同程度的剪切攻击和剪切攻击后的解密图像 (a)垂直剪切10%; (b)垂直剪切50%; (c)水平剪切10%; (d)水平剪切50%; (e)中心剪切; (f)边角剪切; (a')垂直剪切10%解密图; (b')垂直剪切50%解密图; (c')水平剪切10%解密图; (d')水平剪切50%解密图; (e')中心剪切解密图; (f')边角剪切解密图
Figure 9. Cropping attack of different degrees in horizontal, vertical, central, corner directions and decrypted image after cropping attack: (a) Vertical cropping 10%; (b) vertical cropping 50%; (c) horizontal cropping 10%; (d) horizontal cropping 50%; (e) central cropping; (f) corner cropping; (a') decrypted image after vertical cropping 10%; (b') decrypted image after vertical cropping 50%; (c') decrypted image after horizontal cropping 10%; (d') decrypted image after horizontal cropping 50%; (e') decrypted image after central cropping; (f') decrypted image after corner cropping.
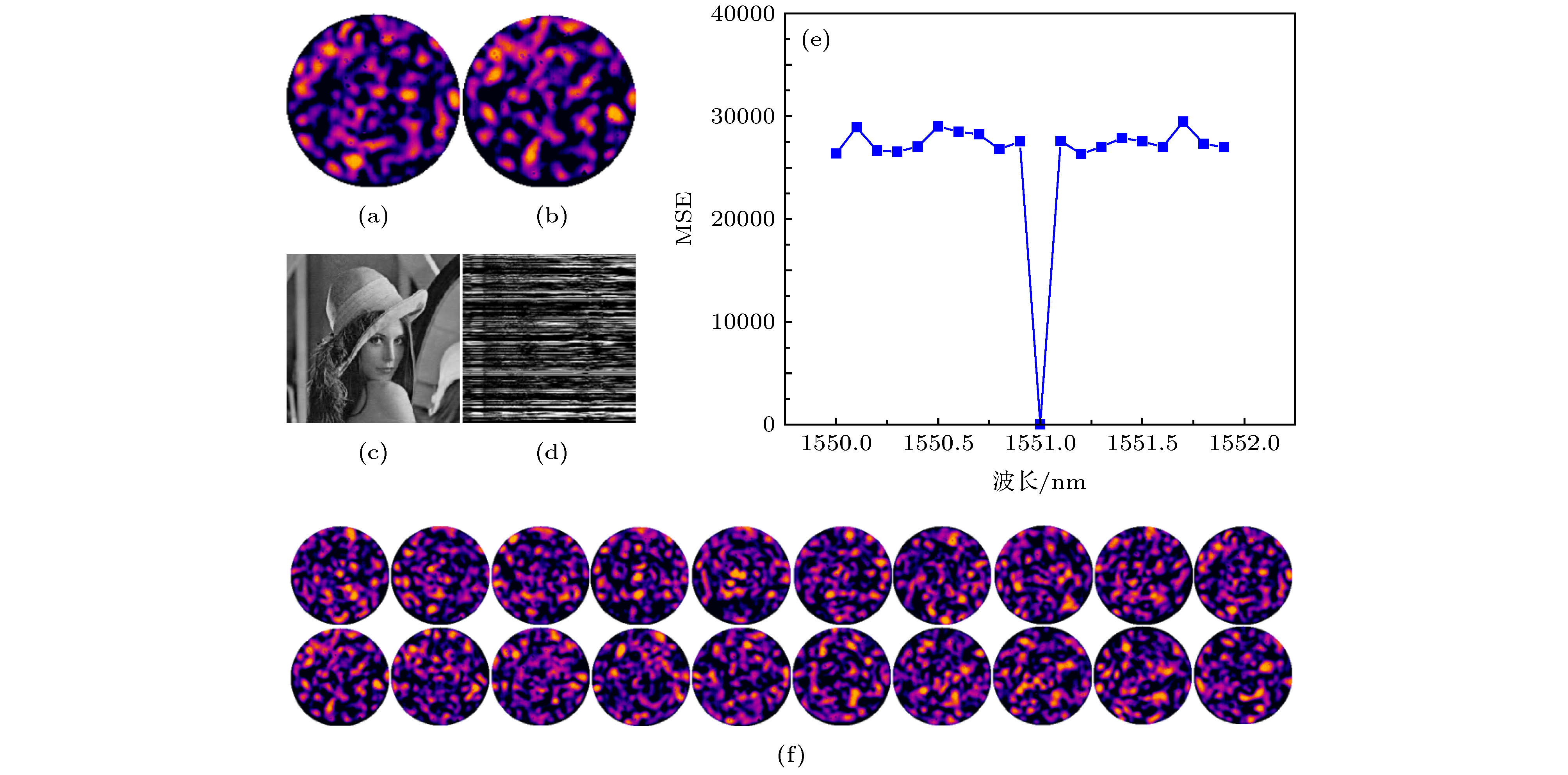
图 10 光斑密钥敏感性分析 (a)原始的光斑密钥; (b)修改后的光斑密钥; (c)与(a)相对应的解密图像; (d)与(b)相对应的解密图像; (e)使用1550−1551.9 nm (间隔为0.1 nm)工作波长产生的光斑进行解密的MSE曲线; (f)对应于(e)中使用的实验测得的不同工作波长光斑
Figure 10. Specklegram key sensitivity analysis: (a) Original specklegram key; (b) modified specklegram key; (c) decrypted image corresponding to (a); (d) decrypted image corresponding to (b); (e) MSE curve for decryption using specklegram generated at different wavelengths; (f) the corresponding specklegram at 1550−1551.9 nm with a wavelength interval of 0.1 nm.
表 1 解密图像质量分析
Table 1. Decrypted image quality analysis.
DownLoad: CSV
表 2 相邻像素的相关系数
Table 2. Correlation coefficient of adjacent pixels.
图像 水平方向 垂直方向 对角方向 
明文图像 0.9359 0.9687 0.9262 密文图像 0.0018 0.0034 0.0010 
明文图像 0.9355 0.9581 0.9161 密文图像 0.0071 0.0052 0.0009 
明文图像 0.9681 0.9562 0.9398 密文图像 0.0023 0.0094 0.0005
DownLoad: CSV
表 3 加密图像像素相关系数
Table 3. Correlation coefficient of encrypted image pixels.
DownLoad: CSV
-
[1] Javidi B 2005 Optical and Digital Techniques for Information Security (New York: Springer Business Media) pp36–40
[2] Refregier P, Javidi B 1995 Opt. Lett. 20 767
Google Scholar
[3] Javidi B 1997 Phys. Today 50 27
Google Scholar
[4] Unnikrishnan G, Joseph J, Singh K 2000 Opt. Lett. 25 887
Google Scholar
[5] Zhu B, Liu S, Ran Q 2000 Opt. Lett. 25 1159
Google Scholar
[6] Situ G H, Zhang J J 2004 Opt. Lett. 29 1584
[7] Chen L F, Zhao D M 2005 Opt. Commun. 254 361
Google Scholar
[8] Peng X, Zhang P, Wei H, Yu B 2006 Opt. Lett. 31 1044
Google Scholar
[9] Guo C, Liu S, Sheridan J T 2015 Appl. Opt. 54 4709
Google Scholar
[10] Li G W, Yang W Q, Li D Y, Situ G H 2017 Opt. Express 25 8690
Google Scholar
[11] Candes E, Romberg J, Tao T 2006 Commun. Pur. Appl. Math. 59 1207
Google Scholar
[12] Donoho D L 2006 IEEE Trans. Inform. Theory 52 1289
Google Scholar
[13] 肖迪, 谢沂均 2013 62 240508
Google Scholar
Xiao D, Xie Y J 2013 Acta Phys. Sin. 62 240508
Google Scholar
[14] 杨华千, 廖晓峰, Kwok-Wo Wong, 张伟, 韦鹏程 2012 61 040505
Google Scholar
Yang H Q, Liao X F, Kwok W W, Zhang W, Wang P C 2012 Acta Phys. Sin. 61 040505
Google Scholar
[15] Deepan B, Quan C, Wang Y, Tay C J 2014 Appl. Opt. 53 4539
Google Scholar
[16] Rawat N, Kim B, Muniraj I, Situ G, Lee B G 2015 Appl. Opt. 54 1782
Google Scholar
[17] Zhou N R, Li H L, Wang D, Pan S M, Zhou Z H 2015 Opt. Commun. 343 10
Google Scholar
[18] Lu P, Xu Z Y, Lu X, Liu X Y 2013 Optik 124 2514
Google Scholar
[19] Liu X Y, Cao Y P, Lu P, Li Y 2013 Optik 124 6590
Google Scholar
[20] Zhou N R, Zhang A D, Zheng F, Gong L H 2014 Opt. Laser Technol. 62 152
[21] Liu H, Xiao D, Liu Y B, Zhang Y S 2015 Optik 126 2663
Google Scholar
[22] Candès E J, Wakin M B 2008 IEEE Signal Proc. Mag. 25 21
Google Scholar
[23] Amphawan A, Payne F, O'Brien D, Shah N 2010 J. Lightwave Technol. 28 861
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 10906
- PDF Downloads: 181
- Cited By: 0
