光电管耦合FitzHugh-Nagumo神经元的同步

张秀芳; 马军; 徐莹; 任国栋

doi:10.7498/aps.70.20201953

摘要

感光细胞能接收各种强度的可见光, 并转换为生物电信号连接视神经; 这样的功能可以用光电效应来模拟. 本文利用数值计算, 分析了基于光电管耦合FitzHugh-Nagumo (FHN)神经元的动力学特性, 详细讨论了光电管的参数空间中, 混沌和簇放电模式下耦合系统的同步区间. 结果表明: 在耦合强度较小时, 耦合系统由于受迫共振表现为完全同步; 耦合强度较大时, 耦合系统倾向于相位同步. 光电管的导通状态, 即反向截止电压对系统同步具有调制作用. 这项工作有助于理解视网膜疾病, 如黄斑变性的原理.

关键词:

神经元 /
光电管 /
同步 /
相位锁定

Abstract

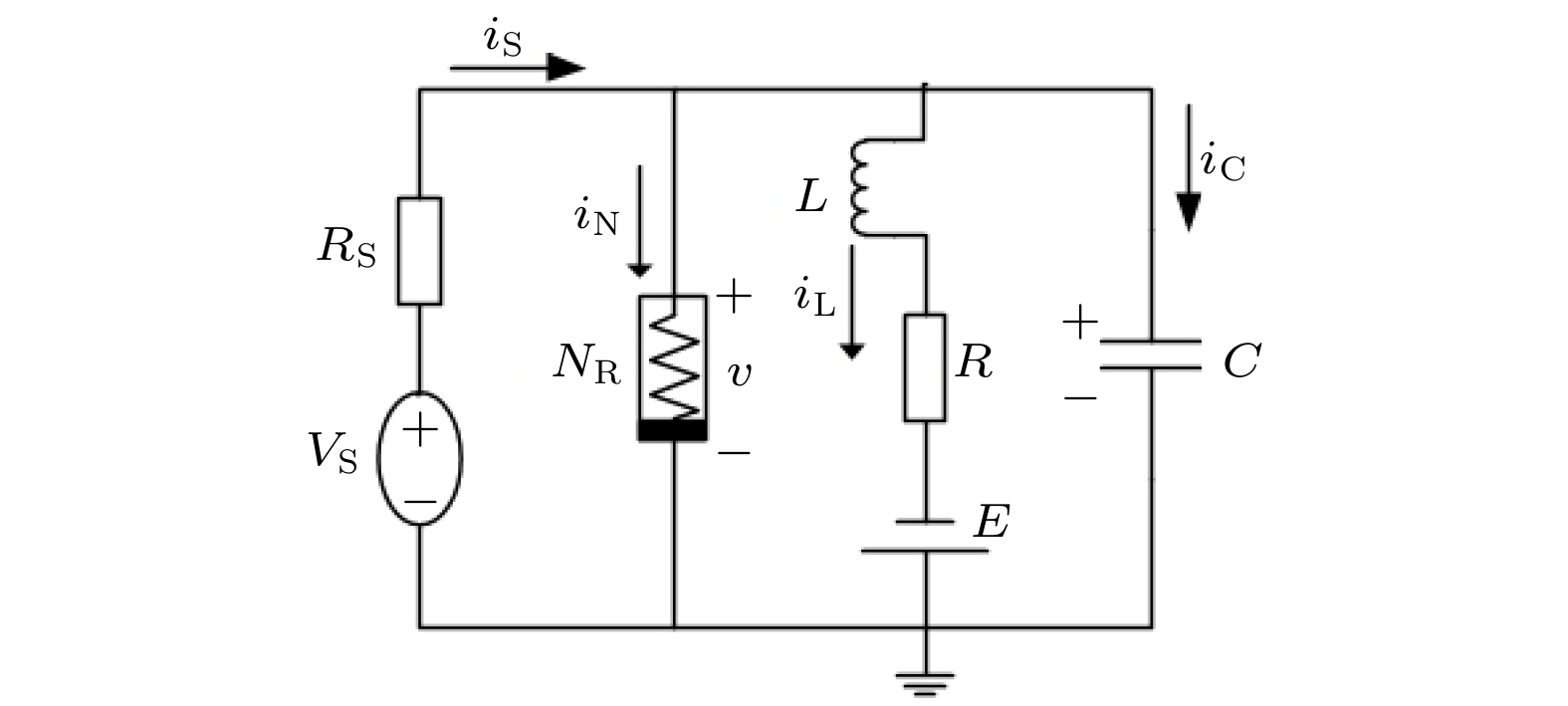
The photoreceptors can receive all kinds of visible light which is translated to the bioelectrical signal for the visual cortex. The function would be simulated by the photoelectric effect. This paper studies the dynamic characteristics of FitzHugh-Nagumo neurons coupled with a phototube. In the parameter space of phototube, the synchronization region of the coupled system in which the neuron mode is in chaos and burst, is discussed in detail; the data show that the forced resonance is prominent in the complete synchronization of the system when the coupling strength is low, while the phase synchronization is observed in numerical experiment when the coupling strength is strong. The active operation of the phototube, as well the inverse cutoff voltage can modulate the synchronization of the system. Our work can be used to understand the mechanism of the retinal diseases, such as macular degeneration.

Keywords:

作者及机构信息

1.
兰州理工大学物理系, 兰州　730050

2.
山东师范大学数学与统计学院, 济南　250014

通信作者: 任国栋, rengd@lut.edu.cn

基金项目: 国家自然科学基金 (批准号:11672122, 12062009) 和甘肃省自然科学基金(批准号: 20JR5RA473)资助的课题

Authors and contacts

1.
Department of Physics, Lanzhou University of Technology, Lanzhou 730050, China

2.
School of Mathematics and Statistics, Shandong Normal University, Ji’nan 250014, China

Corresponding author: Ren Guo-Dong, rengd@lut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11672122, 12062009) and the Natural Science Foundation of Gansu Province, China (Grant No. 20JR5RA473)

文章全文 : translate this paragraph

参考文献

[1]	Ma J, Song X, Jin W, Wang C 2015 Chaos, Solitons Fractals 80 31 Google Scholar
[2]	Iqbal M, Rehan M, Hong K S 2017 Plos One 12 e0176986 Google Scholar
[3]	Sotero R C, Trujillo-Barreto N J 2008 Neuroimage 39 290 Google Scholar
[4]	Izhikevich E M 2004 IEEE Trans. Neural Networks 15 1063 Google Scholar
[5]	Ibarz B, Casado J M, Sanjuán M A F 2011 Phys. Rep. 501 1 Google Scholar
[6]	Hodgkin A L, Huxley A F 1990 Bull. Math. Biol. 52 25 Google Scholar
[7]	Fitzhugh R 1961 Biophys. J. 1 445 Google Scholar
[8]	Shilnikov A 2012 Nonlinear Dyn. 68 305 Google Scholar
[9]	Miesenbock G, Kevrekidis I G 2005 Annu. Rev. Neurosci. 28 533 Google Scholar
[10]	Gu H, Pan B 2015 Nonlinear Dyn. 81 2107 Google Scholar
[11]	Pikovskii A, Rabinovich M 1978 Dokl. Akad. Nauk SSSR 239 301
[12]	Lv M, Wang C, Ren G, Ma J, Song X 2016 Nonlinear Dyn. 85 1479 Google Scholar
[13]	Baines P G 2008 Prog. Phys. Geogr. 32 475 Google Scholar
[14]	Zhang X, Wang C, Ma J, Ren G 2020 Mod. Phys. Lett. B 2050267 Google Scholar
[15]	Zhang G, Ma J, Alsaedi A, Ahmad B, Alzahrani F 2018 Appl. Math. Comput. 321 290 Google Scholar
[16]	Yao Z, Ma J, Yao Y, Wang C 2019 Nonlinear Dyn. 96 205 Google Scholar
[17]	Xu Y M, Yao Z, Hobiny A, Ma J 2019 Front. Inform. Tech. El. 20 571 Google Scholar
[18]	Liu Z, Wang C, Jin W, Ma J 2019 Nonlinear Dyn. 97 2661 Google Scholar
[19]	Tosini G, Doyle S, Geusz M, Menaker M 2000 Proc. Natl. Acad. Sci. 97 11540 Google Scholar
[20]	Menaker M 1972 Sci. Am. 226 22 Google Scholar
[21]	Kennedy D 1958 Am. J. Ophthal. 46 19 Google Scholar
[22]	Martenson M E, Halawa O I, Tonsfeldt K J, et al. 2016 Pain 157 868 Google Scholar
[23]	Liu Y, Xu W J, Ma J, Alzahrani F, Hobiny A 2020 Front. Inform. Tech. El. 21 1387 Google Scholar
[24]	Li J R, Wang J P, Jiang L 1994 Biosens. Bioelectron. 9 147 Google Scholar
[25]	Zou W, Senthilkumar D V, Zhan M, Kurths J 2013 Phys. Rev. Lett. 111 014101 Google Scholar
[26]	Wu Y, Xiao J, Hu G, Zhan M 2012 EPL 97 40005 Google Scholar
[27]	Perc M 2009 Biophys. Chem. 141 175 Google Scholar
[28]	Lin W, Wang Y, Ying H, Lai Y C, Wang X 2015 Phys. Rev. E 92 012912 Google Scholar
[29]	张平伟, 唐国宁, 罗晓曙 2005 54 3497 Google Scholar Zhang P W, Tang G N, Luo X S 2005 Acta Phys. Sin. 54 3497 Google Scholar
[30]	Wouapi K M, Fotsin B H, Louodop F P, Feudjio K F, Njitacke Z T, Djeudjo T H 2020 Cogn. Neurodyn. 14 375 Google Scholar
[31]	Shafiei M, Jafari S, Parastesh F, Ozer M, Kapitaniak T, Perc M 2020 Commun. Nonlinear Sci. Numer. Simul. 84 105175 Google Scholar
[32]	Phan C, You Y 2020 Nonlinear. Anal.-Real 55 103139 Google Scholar
[33]	Moayeri M M, Rad J A, Parand K 2020 Comput. Math. Appl. 80 1887 Google Scholar
[34]	Makovkin S Y, Shkerin I V, Gordleeva S Y, Ivanchenko M V 2020 Chaos, Solitons Fractals 138 109951 Google Scholar
[35]	Zou Y L, Zhu J, Chen G, Luo X S 2005 Chaos, Solitons Fractals 25 1245 Google Scholar
[36]	Zhou S, Hong Y, Yang Y, Lü L, Li C 2020 Pramana J. Phys. 94 34 Google Scholar
[37]	Venkatesh P, Venkatesan A, Lakshmanan M 2016 Pramana J. Phys. 86 1195 Google Scholar
[38]	Sivaganesh G, Sweetlin M D, Arulgnanam A 2016 J. Korean Phys. Soc. 69 124 Google Scholar
[39]	Binczak S, Jacquir S, Bilbault J M, Kazantsev V B, Nekorkin V I 2006 Neural Networks 19 684 Google Scholar
[40]	Wade J J, Mcdaid L J, Harkin J, Crunelli V, Kelso J S 2011 PloS One 6 e29445 Google Scholar
[41]	Sambas A, WS M S, Mamat M 2015 J. Eng. Sci. Tech. Rev. 8 89 Google Scholar
[42]	Daoudal G, Hanada Y, Debanne D 2002 PNAS 99 14512 Google Scholar
[43]	Chorev E, Brecht M 2012 J. Neurophysiol. 108 1584 Google Scholar
[44]	杨永霞, 李玉叶, 古光华 2020 69 040501 Google Scholar Yhang Y X, Li Y Y, Gu G H 2020 Acta Phys. Sin. 69 040501 Google Scholar
[45]	汪芃, 李倩昀, 唐国宁 2018 67 030502 Google Scholar Wang P, Li Q Y, Tang G N 2018 Acta Phys. Sin. 67 030502 Google Scholar
[46]	FitzHugh R 1955 Bull. Math. Biophys. 17 257 Google Scholar
[47]	Nagumo J, Arimoto S, Yoshizawa S 1962 Proc. IRE 50 2061 Google Scholar
[48]	Kawato M, Suzuki R 1980 J. Theor. Biol. 86 547 Google Scholar
[49]	Okuda M 1981 Prog. Theor. Phys. 66 90 Google Scholar
[50]	Treutlein H, Schulten K 1985 Ber. Bunse. Ges. Phys. Chem. 89 710 Google Scholar
[51]	Rajasekar S, Lakshmanan M 1988 J. Theor. Biol. 133 473 Google Scholar
[52]	Einstein A 1905 Ann. Physik. 17 132

施引文献

图 1 FHN神经元的等效电路图

Fig. 1. Equivalent circuit diagram of FHN neuron.

下载: 全尺寸图片幻灯片

图 2 光电管的电流-电压特性

Fig. 2. I-V characteristics of phototube.

下载: 全尺寸图片幻灯片

图 3 光电管耦合FHN神经元系统的等效电路图

Fig. 3. Equivalent circuit diagram of the coupled FHN neuron system.

下载: 全尺寸图片幻灯片

图 4 单个FHN神经元在不同参数下的ISI　(a) b = 0.8, c = 0.1; (b) a = 0.7, c = 0.1; (c) a = 0.7, b = 0.8

Fig. 4. ISI of single FHN neuron with different parameters: (a) b = 0.8, c = 0.1; (b) a = 0.7, c = 0.1; (c) a = 0.7, b = 0.8.

下载: 全尺寸图片幻灯片

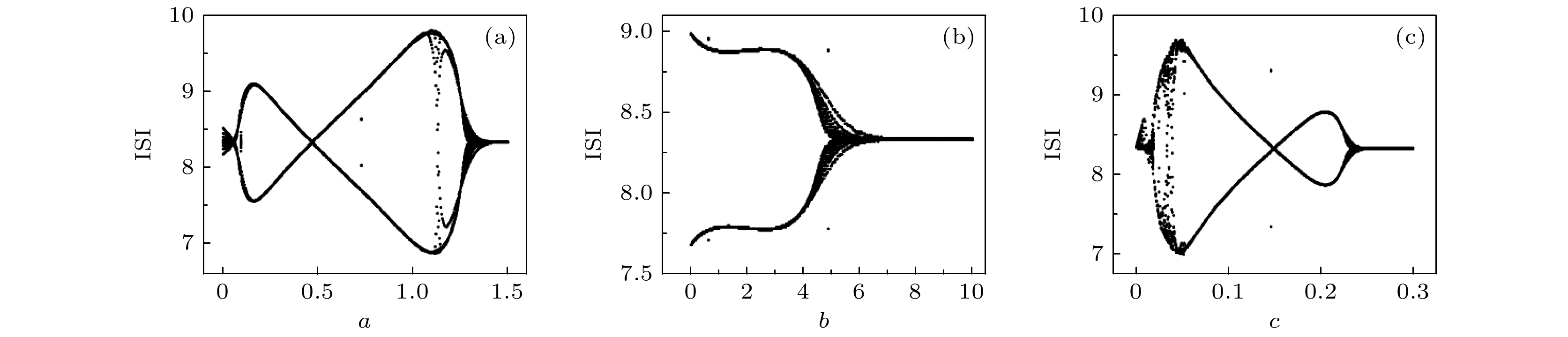
图 5 耦合系统中神经元的ISI和放电序列(f = 0.16)　(a) u_a = 0.1; (b) I₀ = 1.5, u_a = 0.1; (c) I₀ = 2.5, u_a = 0.1; (d) I₀ = 0.3; (e) u_a = 1.5, I₀ = 0.3; (f) u_a = 2.3, I₀ = 0.3

Fig. 5. ISI and the firing sequence of neuron in the coupled system (f = 0.16): (a) u_a = 0.1; (b) I₀ = 1.5, u_a = 0.1; (c) I₀ = 2.5, u_a = 0.1; (d) I₀ = 0.3; (e) u_a = 1.5, I₀ = 0.3; (f) u_a = 2.5, I₀ = 0.3.

下载: 全尺寸图片幻灯片

图 6 u_a和I₀的参数空间中, 耦合系统(case 1)的同步区间　(a)最大误差函数θ_max; (b)最大相位差∆ϕ_max

Fig. 6. Synchronization region of the coupled system (case 1) in the parameter space of u_a vs. I₀: (a) Maximum error function θ_max; (b) maximum phase difference ∆ϕ_max.

下载: 全尺寸图片幻灯片

图 7 误差函数、相位差和功率随时间的演化(u_a = 0.1)　(a), (e), (i) I₀ = 0.01; (b), (f), (j) I₀ = 0.2; (c), (g), (k) I₀ = 0.8; (d), (h), (l) I₀ = 1

Fig. 7. Evolution of error function, phase difference and power (u_a = 0.1): (a), (e), (i) I₀ = 0.01; (b), (f), (j) I₀ = 0.2; (c), (g), (k) I₀ = 0.8; (d), (h), (l) I₀ = 1.

下载: 全尺寸图片幻灯片

图 8 系统误差与相位差随时间的演化(u_a = 0.5)　(a), (e) I₀ = 0.01; (b), (f) I₀ = 0.2; (c), (g) I₀ = 0.8; (d), (h) I₀ = 1

Fig. 8. Evolution of error function and phase error (u_a = 0.5): (a), (e) I₀ = 0.01; (b), (f) I₀ = 0.2; (c), (g) I₀ = 0.8; (d), (h) I₀ = 1.

下载: 全尺寸图片幻灯片

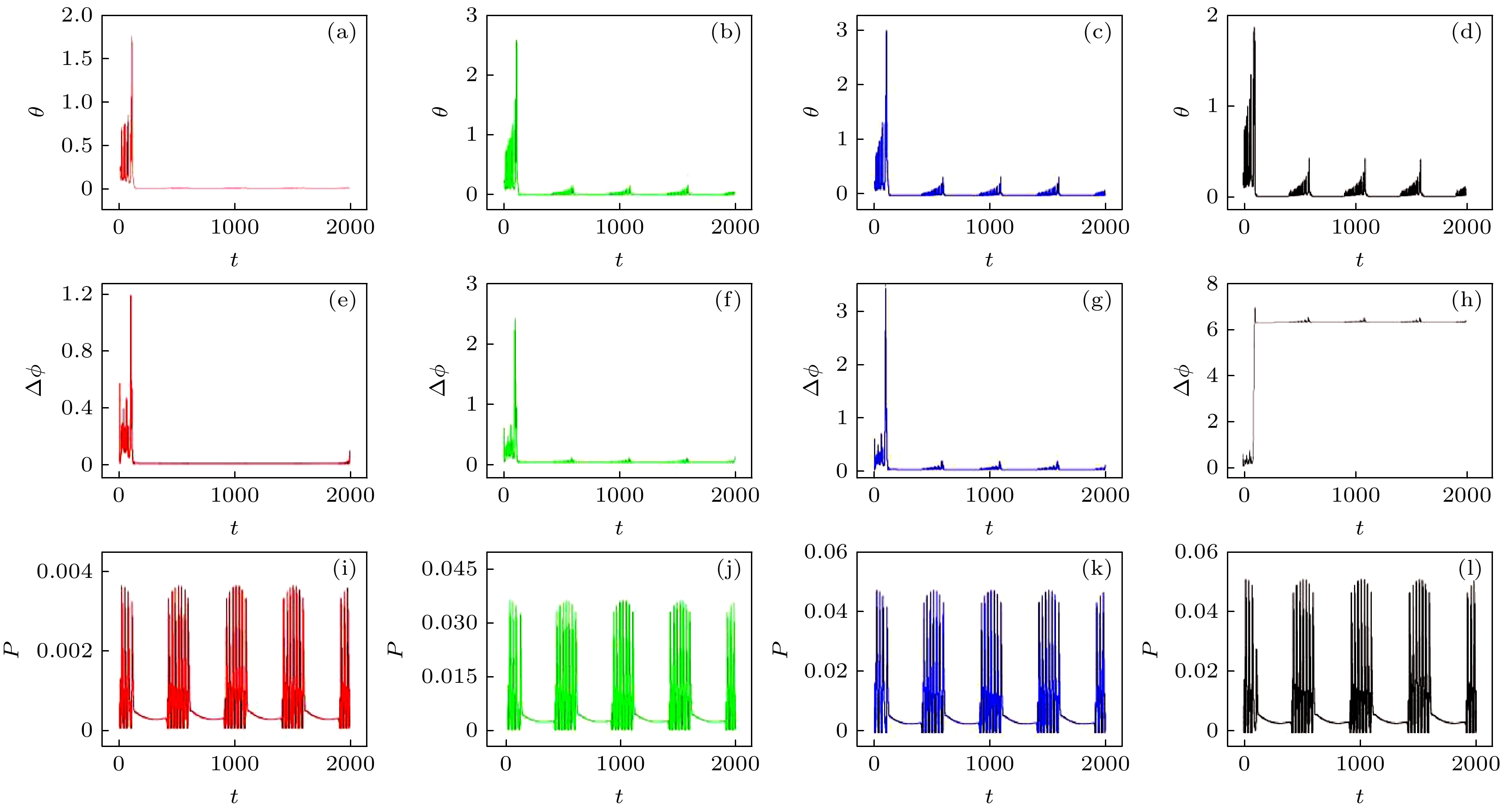
图 9 耦合系统中神经元的ISI和放电序列(f = 0.002)　(a) u_a = 0.01; (b) I₀ = 0.5, u_a = 0.01; (c) I₀ = 1.5, u_a = 0.01; (d) I₀ = 0.3; (e) u_a = 0.5, I₀ = 0.3; (f) u_a = 1.5, I₀ = 0.3

Fig. 9. ISI and the firing sequence of neuron in the coupled system (f = 0.002): (a) u_a = 0.01; (b) I₀ = 0.5, u_a = 0.1; (c) I₀ = 1.5, u_a = 0.1; (d) I₀ = 0.3; (e) u_a = 0.5, I₀ = 0.3; (f) u_a = 1.5, I₀ = 0.3.

下载: 全尺寸图片幻灯片

图 10 u_a和I₀的参数空间中, 耦合系统(case 3)的同步区间　(a)最大误差函数θ_max; (b)最大相位差∆ϕ_max

Fig. 10. Synchronization region of the coupled system (case 3) in the parameter space of u_a vs. I₀: (a) Maximum error function θ_max; (b) maximum phase difference ∆ϕ_max.

下载: 全尺寸图片幻灯片

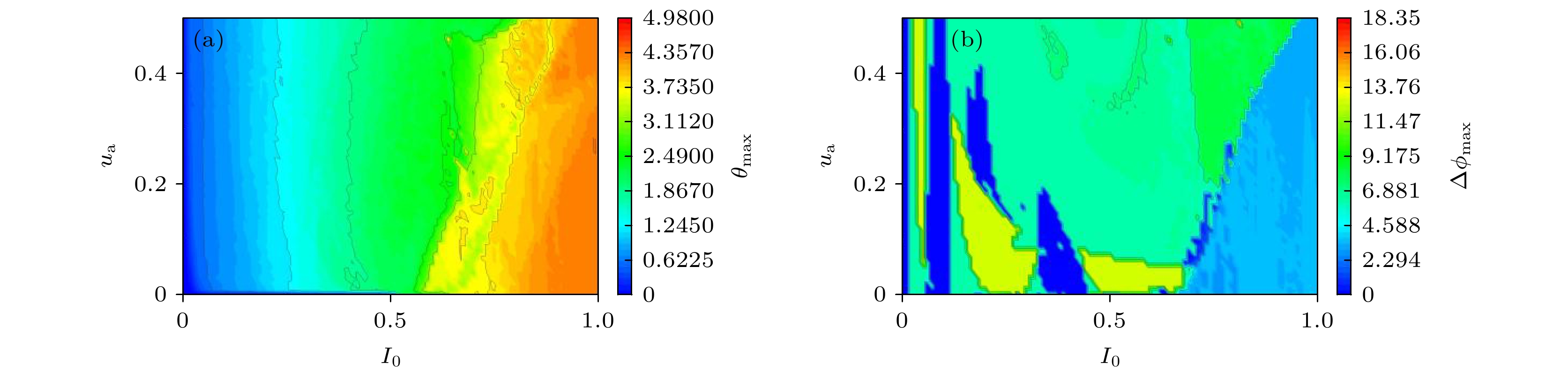
图 11 最大误差函数和最大相位差随参数的变化(灰色曲线为(6)式中的非线性耦合, 红色曲线为线性耦合)　(a), (b) u_a = 0.01; (c), (d) I₀ = 0.001

Fig. 11. The maximum error function and the maximum phase difference change with the parameters, the grey curve represents the nonlinear coupling in Eq. (6) and the red curve is the linear one: (a), (b) u_a = 0.01; (c), (d) I₀ = 0.001.

下载: 全尺寸图片幻灯片

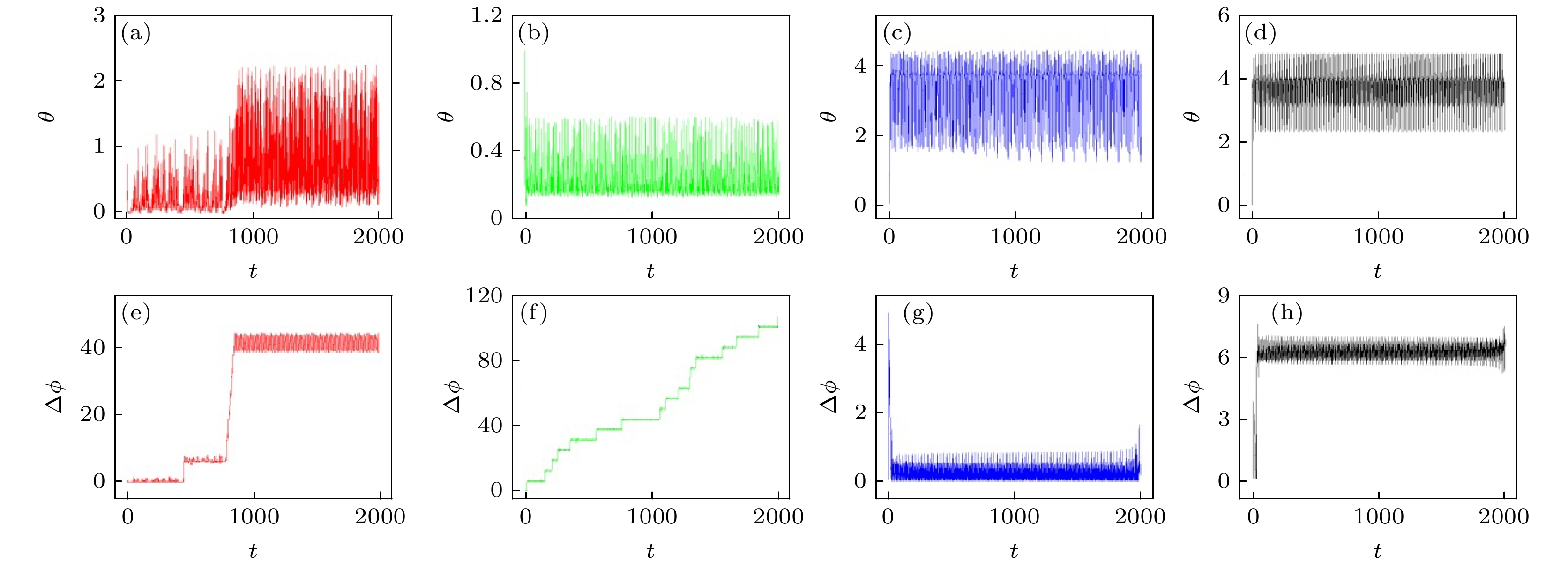
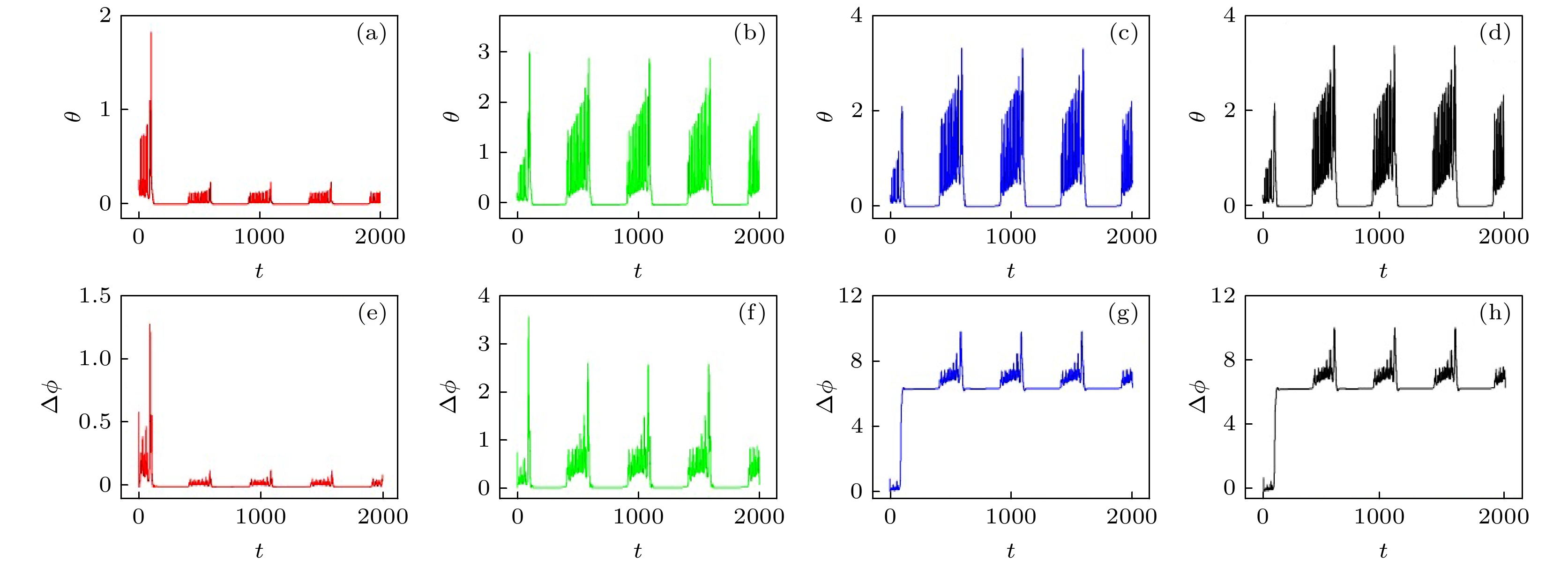
图 12 系统误差、相位差和光电管功率随时间的演化(u_a = 0.01)　(a), (e), (i) I₀ = 0.001; (b), (f), (j) I₀ = 0.01; (c), (g), (k) I₀ = 0.013; (d), (h), (l) I₀ = 0.014

Fig. 12. Evolution of error function, phase error and phototube power (u_a = 0.01): (a), (e), (i) I₀ = 0.001; (b), (f), (j) I₀ = 0.01; (c), (g), (k) I₀ = 0.013; (d), (h), (l) I₀ = 0.014.

下载: 全尺寸图片幻灯片

图 13 系统误差与相位差随时间的演化(u_a = 0.5)　(a), (e) I₀ = 0.001; (b), (f) I₀ = 0.01; (c), (g) I₀ = 0.013; (d), (h) I₀ = 0.014

Fig. 13. Evolution of error function and phase error for variables (u_a = 0.5): (a), (e) I₀ = 0.001; (b), (f) I₀ = 0.01; (c), (g) I₀ = 0.013; (d), (h) I₀ = 0.014.

下载: 全尺寸图片幻灯片

表 1 不同外界刺激频率下的耦合FHN神经元分类

Table 1. Category of the coupled FHN neurons driven by external stimulation with different frequencies.

频率f 0.16 0.002 0.012 0.06

放电状态混沌放电簇放电尖峰放电周期放电
反向截止电压u_a 0.1 0.5 0.01 0.5 0.01 0.5 0.01 0.5

耦合分类 case 1 case 2 case 3 case 4 case 5 case 6 case 7 case 8

下载: 导出CSV

map

[1]	Ma J, Song X, Jin W, Wang C 2015 Chaos, Solitons Fractals 80 31 Google Scholar
[2]	Iqbal M, Rehan M, Hong K S 2017 Plos One 12 e0176986 Google Scholar
[3]	Sotero R C, Trujillo-Barreto N J 2008 Neuroimage 39 290 Google Scholar
[4]	Izhikevich E M 2004 IEEE Trans. Neural Networks 15 1063 Google Scholar
[5]	Ibarz B, Casado J M, Sanjuán M A F 2011 Phys. Rep. 501 1 Google Scholar
[6]	Hodgkin A L, Huxley A F 1990 Bull. Math. Biol. 52 25 Google Scholar
[7]	Fitzhugh R 1961 Biophys. J. 1 445 Google Scholar
[8]	Shilnikov A 2012 Nonlinear Dyn. 68 305 Google Scholar
[9]	Miesenbock G, Kevrekidis I G 2005 Annu. Rev. Neurosci. 28 533 Google Scholar
[10]	Gu H, Pan B 2015 Nonlinear Dyn. 81 2107 Google Scholar
[11]	Pikovskii A, Rabinovich M 1978 Dokl. Akad. Nauk SSSR 239 301
[12]	Lv M, Wang C, Ren G, Ma J, Song X 2016 Nonlinear Dyn. 85 1479 Google Scholar
[13]	Baines P G 2008 Prog. Phys. Geogr. 32 475 Google Scholar
[14]	Zhang X, Wang C, Ma J, Ren G 2020 Mod. Phys. Lett. B 2050267 Google Scholar
[15]	Zhang G, Ma J, Alsaedi A, Ahmad B, Alzahrani F 2018 Appl. Math. Comput. 321 290 Google Scholar
[16]	Yao Z, Ma J, Yao Y, Wang C 2019 Nonlinear Dyn. 96 205 Google Scholar
[17]	Xu Y M, Yao Z, Hobiny A, Ma J 2019 Front. Inform. Tech. El. 20 571 Google Scholar
[18]	Liu Z, Wang C, Jin W, Ma J 2019 Nonlinear Dyn. 97 2661 Google Scholar
[19]	Tosini G, Doyle S, Geusz M, Menaker M 2000 Proc. Natl. Acad. Sci. 97 11540 Google Scholar
[20]	Menaker M 1972 Sci. Am. 226 22 Google Scholar
[21]	Kennedy D 1958 Am. J. Ophthal. 46 19 Google Scholar
[22]	Martenson M E, Halawa O I, Tonsfeldt K J, et al. 2016 Pain 157 868 Google Scholar
[23]	Liu Y, Xu W J, Ma J, Alzahrani F, Hobiny A 2020 Front. Inform. Tech. El. 21 1387 Google Scholar
[24]	Li J R, Wang J P, Jiang L 1994 Biosens. Bioelectron. 9 147 Google Scholar
[25]	Zou W, Senthilkumar D V, Zhan M, Kurths J 2013 Phys. Rev. Lett. 111 014101 Google Scholar
[26]	Wu Y, Xiao J, Hu G, Zhan M 2012 EPL 97 40005 Google Scholar
[27]	Perc M 2009 Biophys. Chem. 141 175 Google Scholar
[28]	Lin W, Wang Y, Ying H, Lai Y C, Wang X 2015 Phys. Rev. E 92 012912 Google Scholar
[29]	张平伟, 唐国宁, 罗晓曙 2005 54 3497 Google Scholar Zhang P W, Tang G N, Luo X S 2005 Acta Phys. Sin. 54 3497 Google Scholar
[30]	Wouapi K M, Fotsin B H, Louodop F P, Feudjio K F, Njitacke Z T, Djeudjo T H 2020 Cogn. Neurodyn. 14 375 Google Scholar
[31]	Shafiei M, Jafari S, Parastesh F, Ozer M, Kapitaniak T, Perc M 2020 Commun. Nonlinear Sci. Numer. Simul. 84 105175 Google Scholar
[32]	Phan C, You Y 2020 Nonlinear. Anal.-Real 55 103139 Google Scholar
[33]	Moayeri M M, Rad J A, Parand K 2020 Comput. Math. Appl. 80 1887 Google Scholar
[34]	Makovkin S Y, Shkerin I V, Gordleeva S Y, Ivanchenko M V 2020 Chaos, Solitons Fractals 138 109951 Google Scholar
[35]	Zou Y L, Zhu J, Chen G, Luo X S 2005 Chaos, Solitons Fractals 25 1245 Google Scholar
[36]	Zhou S, Hong Y, Yang Y, Lü L, Li C 2020 Pramana J. Phys. 94 34 Google Scholar
[37]	Venkatesh P, Venkatesan A, Lakshmanan M 2016 Pramana J. Phys. 86 1195 Google Scholar
[38]	Sivaganesh G, Sweetlin M D, Arulgnanam A 2016 J. Korean Phys. Soc. 69 124 Google Scholar
[39]	Binczak S, Jacquir S, Bilbault J M, Kazantsev V B, Nekorkin V I 2006 Neural Networks 19 684 Google Scholar
[40]	Wade J J, Mcdaid L J, Harkin J, Crunelli V, Kelso J S 2011 PloS One 6 e29445 Google Scholar
[41]	Sambas A, WS M S, Mamat M 2015 J. Eng. Sci. Tech. Rev. 8 89 Google Scholar
[42]	Daoudal G, Hanada Y, Debanne D 2002 PNAS 99 14512 Google Scholar
[43]	Chorev E, Brecht M 2012 J. Neurophysiol. 108 1584 Google Scholar
[44]	杨永霞, 李玉叶, 古光华 2020 69 040501 Google Scholar Yhang Y X, Li Y Y, Gu G H 2020 Acta Phys. Sin. 69 040501 Google Scholar
[45]	汪芃, 李倩昀, 唐国宁 2018 67 030502 Google Scholar Wang P, Li Q Y, Tang G N 2018 Acta Phys. Sin. 67 030502 Google Scholar
[46]	FitzHugh R 1955 Bull. Math. Biophys. 17 257 Google Scholar
[47]	Nagumo J, Arimoto S, Yoshizawa S 1962 Proc. IRE 50 2061 Google Scholar
[48]	Kawato M, Suzuki R 1980 J. Theor. Biol. 86 547 Google Scholar
[49]	Okuda M 1981 Prog. Theor. Phys. 66 90 Google Scholar
[50]	Treutlein H, Schulten K 1985 Ber. Bunse. Ges. Phys. Chem. 89 710 Google Scholar
[51]	Rajasekar S, Lakshmanan M 1988 J. Theor. Biol. 133 473 Google Scholar
[52]	Einstein A 1905 Ann. Physik. 17 132

[1]	马少卿, 龚士香, 张微, 路承彪, 李小俚, 李英伟. 宽带微量太赫兹辐射促进神经元生长发育. , 2022, 71(20): 208701. doi: 10.7498/aps.71.20220636
[2]	白婧, 关富荣, 唐国宁. 神经元网络中局部同步引发的各种效应. , 2021, 70(17): 170502. doi: 10.7498/aps.70.20210142
[3]	谢盈, 朱志刚, 张晓锋, 任国栋. 光电流驱动下非线性神经元电路的放电模式控制. , 2021, 70(21): 210502. doi: 10.7498/aps.70.20210676
[4]	魏天丽, 吴德伟, 杨春燕, 罗均文, 苗强, 李响. 一种双模压缩微波制备的相位锁定方案. , 2020, 69(3): 034204. doi: 10.7498/aps.69.20191348
[5]	于文婷, 张娟, 唐军. 动态突触、神经耦合与时间延迟对神经元发放的影响. , 2017, 66(20): 200201. doi: 10.7498/aps.66.200201
[6]	修春波, 刘畅, 郭富慧, 成怡, 罗菁. 迟滞混沌神经元/网络的控制策略及应用研究. , 2015, 64(6): 060504. doi: 10.7498/aps.64.060504
[7]	王付霞, 谢勇. "Hopf/homoclinic"簇放电和"SubHopf/homoclinic"簇放电之间的同步. , 2013, 62(2): 020509. doi: 10.7498/aps.62.020509
[8]	吴望生, 唐国宁. 不同耦合下混沌神经元网络的同步. , 2012, 61(7): 070505. doi: 10.7498/aps.61.070505
[9]	王兴元, 任小丽, 张永雷. 参数未知神经元模型的全阶与降阶最优同步. , 2012, 61(6): 060508. doi: 10.7498/aps.61.060508
[10]	陈军, 李春光. 禁忌学习神经元模型的电路设计及其动力学研究. , 2011, 60(2): 020502. doi: 10.7498/aps.60.020502
[11]	王争, 赵新杰, 何明, 周铁戈, 岳宏卫, 阎少林. 嵌入到Fabry-Perot谐振腔的双晶约瑟夫森结阵列的阻抗匹配和相位锁定研究. , 2010, 59(5): 3481-3487. doi: 10.7498/aps.59.3481
[12]	何国光, 朱萍, 陈宏平, 谢小平. 阈值耦合混沌神经元的同步研究. , 2010, 59(8): 5307-5312. doi: 10.7498/aps.59.5307
[13]	刘勇, 谢勇. 分数阶FitzHugh-Nagumo模型神经元的动力学特性及其同步. , 2010, 59(3): 2147-2155. doi: 10.7498/aps.59.2147
[14]	王慧巧, 俞连春, 陈勇. 离子通道噪声对神经元新陈代谢能量的影响. , 2009, 58(7): 5070-5074. doi: 10.7498/aps.58.5070
[15]	乔晓艳, 李刚, 董有尔, 贺秉军. 弱激光诱导神经元兴奋性改变的实验研究. , 2008, 57(2): 1259-1265. doi: 10.7498/aps.57.1259
[16]	雷兵, 冯莹, 刘泽金. 利用全光纤耦合环实现三路光纤激光器的相位锁定. , 2008, 57(10): 6419-6424. doi: 10.7498/aps.57.6419
[17]	乔晓艳, 李刚, 林凌, 贺秉军. 弱激光对神经元钾离子通道特性影响的实验研究. , 2007, 56(4): 2448-2455. doi: 10.7498/aps.56.2448
[18]	王占山, 张化光, 王智良. 一类混沌神经网络的全局同步. , 2006, 55(6): 2687-2693. doi: 10.7498/aps.55.2687
[19]	颜森林. 量子阱激光器混沌相位控制同步以及编码研究. , 2005, 54(3): 1098-1104. doi: 10.7498/aps.54.1098
[20]	吴　王莹, 徐健学, 何岱海, 靳伍银. 两个非耦合Hindmarsh-Rose神经元同步的非线性特征研究. , 2005, 54(7): 3457-3464. doi: 10.7498/aps.54.3457

计量

文章访问数: 6607
PDF下载量: 143
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

光电管耦合FitzHugh-Nagumo神经元的同步