Fano resonances in symmetric gold nanorod trimers

Li Ai-Yun; Zhang Xing-Fang; Liu Feng-Shou; Yan Xin; Liang Lan-Ju

doi:10.7498/aps.68.20190978

Abstract

A symmetrical gold nanorod trimer structure consisting of a short center nanorod and two long nanorods on both sides is proposed. The scattering spectra, electromagnetic field and current density vector distributions across the central cross section of the nanorod trimer are calculated by the finite difference time domain method, and the effects of structural parameters and dielectric environment on Fano resonance characteristics are theoretically investigated in detail. The results show that the Fano resonance can be generated mainly due to the interference between the bonding electric dipole mode in lower energy and the antibonding electric dipole mode or antiphase magnetic dipole mode in higher energy. The Fano dip is blue-shifted with the decrease in the short nanorod length, the size of whole trimer structure with constant displacement, or the refractive index of dielectric medium in the gaps between the central nanorod and two side nanorods; the resonance intensity on both sides of the Fano dip also changes. Meanwhile, the bonding mode on the red side of the Fano dip is gradually dominated by the electric dipole mode of two side nanorods, and the spectral intensity increases, while the antibonding mode on the blue side gradually evolves into the short nanorod-dominated antiphase magnetic dipole mode, and the spectral intensity becomes weaker. The increase in the inter-rod spacing also leads the Fano dip to be blue-shifted, and a similar change in the spectral intensity occurs on both sides of the Fano dip, due to the degeneration of bonding and antibonding modes caused by the decrease of near-field coupling between the short nanorod and two side nanorods, which finally degenerate into the electric dipole modes generated by the short nanorod or the two side nanorods, respectively. In addition, the Fano dip is insensitive to the change of the side nanorod length, but the relative resonance intensity on both sides of the Fano dip also changes. Furthermore, it is found that the spectral contrast ratio of the Fano resonance first increases and then decreases by varying the above-mentioned structural parameters or dielectric environment. These results are expected to be used for guiding the design of Fano controllable nanostructures and also for developing the applications of specific micro-nano photonics.

Keywords:

Authors and contacts

1.
School of Opt-Electronic Engineering, Zaozhuang University, Zaozhuang 277160, China
2.
Laboratory of Optoelectronic Information Processing and Display of Shandong, Zaozhuang 277160, China

Corresponding author: Zhang Xing-Fang, zxf4114@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 61701434), the Natural Science Foundation of Shandong Province, China (Grant Nos. ZR2017MF005, ZR2018LF001), the Project of Shandong Province Higher Education Science and Technology Program, China (Grant No. J17KA087), and the Key Laboratory of Optoelectronic Information Functional Materials and Micronano Devices in Zaozhuang, China

FullText HTML : translate this paragraph

References

[1]	Zhang S P, Xu H X 2016 Nanoscale 8 13722 Google Scholar
[2]	Biswas S, Duan J, Nepal D, Park K, Pachter R, Vaia R A 2013 Nano Lett. 13 6287 Google Scholar
[3]	Artar A, Yanik A A, Altug H 2011 Nano Lett. 11 3694 Google Scholar
[4]	Wu D, Liu C, Liu Y, Yu L, Yu Z, Chen L, Ma R, Ye H 2017 Opt. Lett. 42 450 Google Scholar
[5]	Zhang J, Chen S, Wang J,Mu K, Fan C, Liang E, Ding P 2018 Sci. Rep. 8 740 Google Scholar
[6]	Limonov M F, Rybin M V, Poddubny A N, Kivshar Y S 2017 Nat. Photon. 11 543 Google Scholar
[7]	Chen J, Gan F, Wang Y, Li G 2018 Adv. Opt. Mater. 6 1701152 Google Scholar
[8]	Huang C Y, Chang H C 2019 IEEE Photon. J. 11 4800208 Google Scholar
[9]	Li G Z, Hu H J, Wu L 2019 Phys. Chem. Chem. Phys. 21 7654 Google Scholar
[10]	Wu C, Khanikaev A B, Shvets G 2011 Phys. Rev. Lett. 106 107403 Google Scholar
[11]	Chang W S, Lassiter J B, Swanglap P, Sobhani H, Khatua S, Nordlander P, Halas N J, Link S 2012 Nano Lett. 12 4977 Google Scholar
[12]	Yu Y, Xue W, Semenova E, Yvind K, Mork J 2017 Nat. Photon. 11 81 Google Scholar
[13]	Hu H J, Zhang F W, Li G Z, Chen J Y, Li Q, Wu L J 2018 Photon. Res. 6 204 Google Scholar
[14]	Yang Z J, Hao Z H, Lin H Q, Wang Q Q 2014 Nanoscale 6 4985 Google Scholar
[15]	黄运欢, 李璞 2015 64 207301 Google Scholar Huang Y H, Li P 2015 Acta Phys. Sin. 64 207301 Google Scholar
[16]	Zhang Y, Jia T Q, Zhang H M, Xu Z Z 2012 Opt. Lett. 37 4919 Google Scholar
[17]	Fu Y H, Zhang J B, Yu Y F, Lukyanchuk B 2012 ACS Nano 6 5130 Google Scholar
[18]	Zhao W, Jiang Y 2015 Opt. Lett. 40 93 Google Scholar
[19]	Yang Z J, Wang Q Q, Lin H Q 2013 Appl. Phys. Lett. 103 111115 Google Scholar
[20]	Zhang S, Genov D A, Wang Y, Liu M, Zhang X 2008 Phys. Rev. Lett. 101 047401 Google Scholar
[21]	Wang J, Liu X, Li L, He J, Fan C, Tian Y, Ding P, Chen D, Xue Q, Liang E 2013 J. Opt. 15 105003 Google Scholar
[22]	Dong Z G, Liu H, Xu M X, Li Tao, Wang S M, Zhu S N, Zhang X 2010 Opt. Express 18 18229 Google Scholar
[23]	Jin X R, Park J, Zheng H, Lee S, Lee Y, Rhee J Y, Kim K W, Cheong H S, Jang W H 2011 Opt. Express 19 21652 Google Scholar
[24]	Bozhevolnyi S I, Evlyukhin A B, Pors A, Nielsen M G, Willatzen M, Albrektsen O 2011 New J. Phys. 13 023034 Google Scholar
[25]	Yang Z J, Zhang Z S, Zhang L H, Li Q Q, Hao Z H, Wang Q Q 2011 Opt. Lett. 36 1542 Google Scholar
[26]	Kai G, Zhang Y L, Qian C, Fung K H 2018 Opt. Express 26 11984 Google Scholar
[27]	Liu G D, Zhai X, Wang L L, Wang B X, Lin Q, Shang X J 2016 Plasmonics 11 381 Google Scholar
[28]	Liu S D, Leong E S P, Li G C, Hou Y, Deng J, Teng J H, Ong H C, Lei D Y 2016 ACS Nano 10 1442 Google Scholar
[29]	Wang J, Fan C, He J, Ding P, Liang E, Xue Q 2013 Opt. Express 21 2236 Google Scholar
[30]	Li G, Li Q, Xu L, Wu L 2015 Plasmonics 10 1401 Google Scholar
[31]	丛超, 吴大建, 刘晓峻 2011 60 046102 Google Scholar Cong C, Wu D J, Liu X J 2011 Acta Phys. Sin. 60 046102 Google Scholar
[32]	Taflove A, Hagness S 2000 Computational Electrodynamics: the Finite-Difference Time-Domain Method (Vol. 2) (Boston: Artech House) pp75−85
[33]	Johnson P B, Christy R W 1972 Phys. Rev. B 6 4370 Google Scholar
[34]	Halas N J, Lal S, Chang W S, Nordlander P 2011 Chem. Rev. 111 3913 Google Scholar
[35]	Feng R, Qiu J, Liu L, Ding W, Chen L 2014 Opt. Express 22 A1713 Google Scholar
[36]	Hu X, Huang Y, Yuan S, Liu Y, Jiao Z, Wang Y, Huang Q, Yu J, Xia J 2015 Plasmonics 10 1817 Google Scholar

Cited By

图 1 对称金纳米棒三聚体结构的模型示意图

Figure 1. Geometrical structure of the symmetric Au nanorod trimer structure.

DownLoad: Full-Size Img PowerPoint

图 2 金纳米棒三聚体的散射谱和吸收谱, 插图为在两个散射共振峰位971, 1319和共振谷1229 nm处的纳米结构截面电场和电流密度矢量分布

Figure 2. Scattering and absorption spectra of a single gold nanorod trimer. Insets show the calculated electric field and current density vector distributions across the central cross section of the nanorod trimer at the indicated resonances.

DownLoad: Full-Size Img PowerPoint

图 3 金纳米棒三聚体的散射谱随中间短棒变化的关系, 插图为在指定频率处的纳米结构截面电磁场和电流密度矢量分布

Figure 3. Scattering spectra of the nanorod trimer versus the length of center nanorod L_i. Insets show the calculated electric field, magnetic field in the z-direction and current density vector distributions at the indicated resonances.

DownLoad: Full-Size Img PowerPoint

图 4 金纳米棒三聚体的散射谱随边棒变化的关系, 插图为在指定散射共振峰位处的纳米结构截面电磁场和电流密度矢量分布

Figure 4. Scattering spectra of the nanorod trimer versus the length of side nanorod L_o. Insets show the calculated electric field, magnetic field in the z-direction and current density vector distributions at the indicated resonances.

DownLoad: Full-Size Img PowerPoint

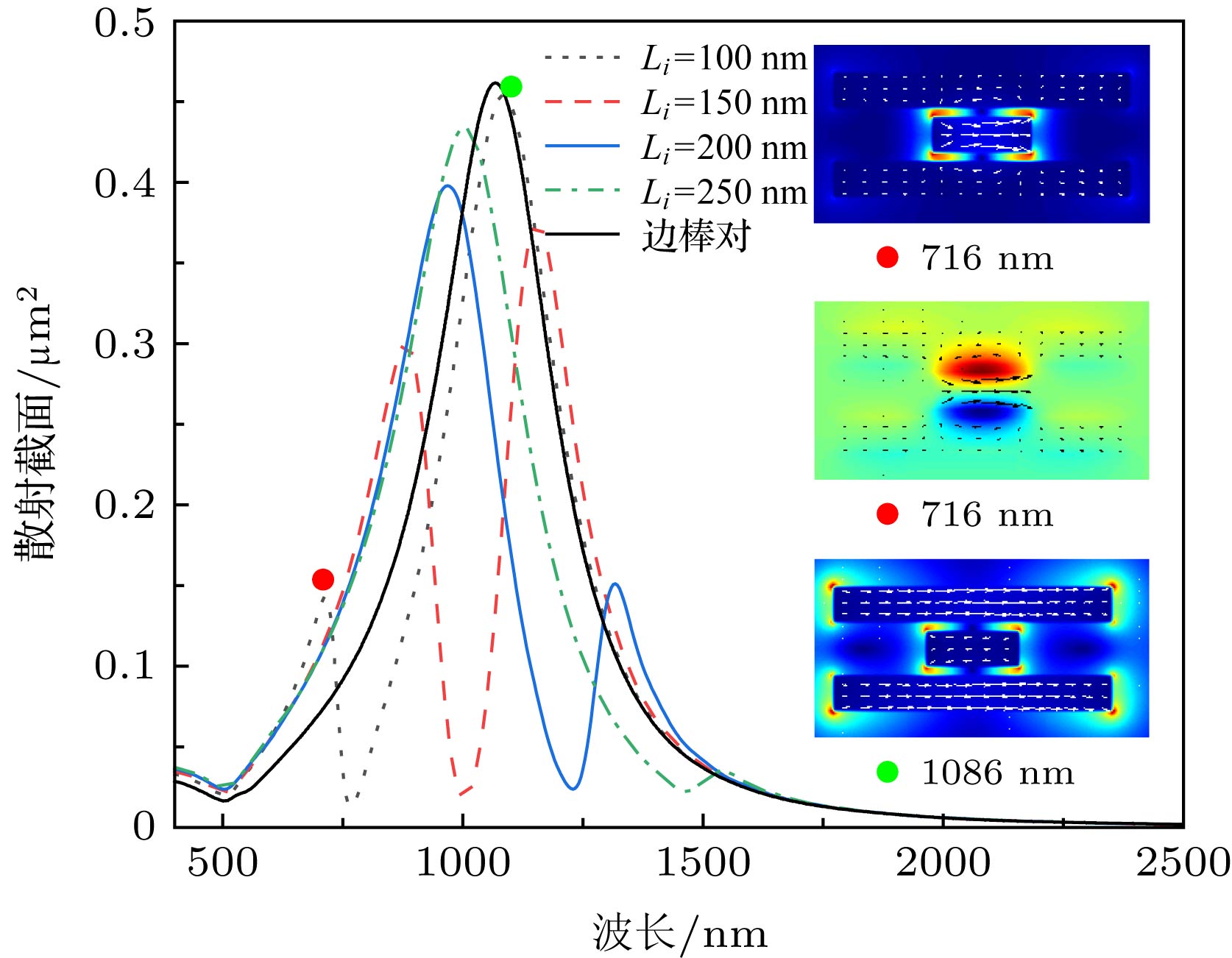
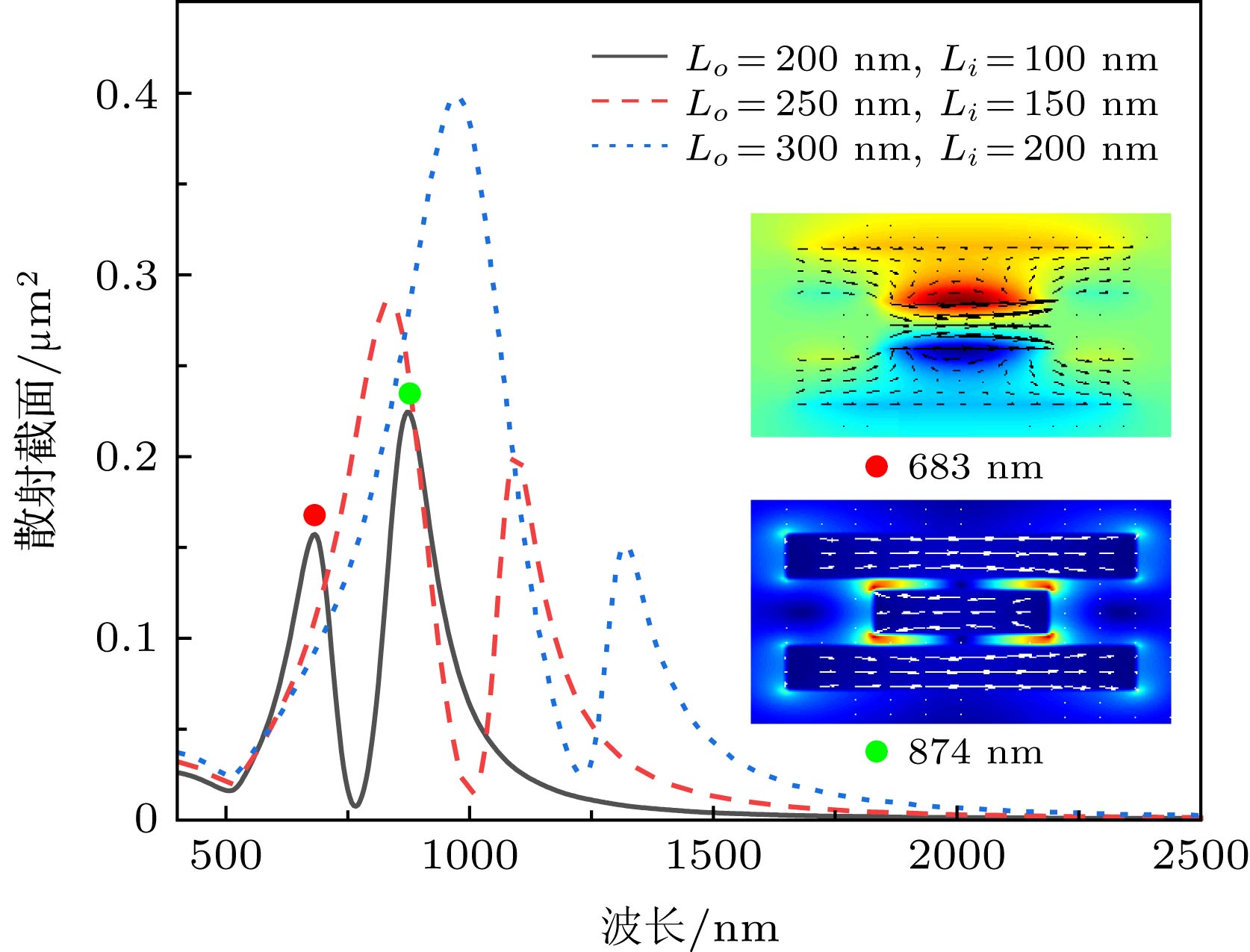
图 5 金纳米棒三聚体的散射谱随三棒尺寸变化的关系, 插图为在指定散射共振峰位处的纳米结构截面电磁场和电流密度矢量分布

Figure 5. Scattering spectra of the nanorod trimer versus the nanorod length with constant displacement ΔL = 100 nm. Insets show the calculated electric field, magnetic field in the z-direction and current density vector distributions at the indicated resonances.

DownLoad: Full-Size Img PowerPoint

图 6 金纳米棒三聚体的散射谱随棒间距变化的关系, 插图为在指定散射共振峰位处的纳米结构截面电场和电流密度矢量分布

Figure 6. Scattering spectra of the nanorod trimer versus inter-rod spacing d. Insets show the calculated electric field and current density vector distributions at the indicated resonances.

DownLoad: Full-Size Img PowerPoint

图 7 当短棒与边棒的间隙内介电环境变化时, 金纳米棒三聚体的散射谱随介质折射率变化的关系, 插图为在两个散射共振峰位处的纳米结构截面电磁场和电流密度矢量分布

Figure 7. Scattering spectra of the nanorod trimer with different media in the gaps between the center and side nanorods. Insets show the calculated electric field, magnetic field in the z-direction and current density vector distributions at the indicated resonances.

DownLoad: Full-Size Img PowerPoint

map

[1]	Zhang S P, Xu H X 2016 Nanoscale 8 13722 Google Scholar
[2]	Biswas S, Duan J, Nepal D, Park K, Pachter R, Vaia R A 2013 Nano Lett. 13 6287 Google Scholar
[3]	Artar A, Yanik A A, Altug H 2011 Nano Lett. 11 3694 Google Scholar
[4]	Wu D, Liu C, Liu Y, Yu L, Yu Z, Chen L, Ma R, Ye H 2017 Opt. Lett. 42 450 Google Scholar
[5]	Zhang J, Chen S, Wang J,Mu K, Fan C, Liang E, Ding P 2018 Sci. Rep. 8 740 Google Scholar
[6]	Limonov M F, Rybin M V, Poddubny A N, Kivshar Y S 2017 Nat. Photon. 11 543 Google Scholar
[7]	Chen J, Gan F, Wang Y, Li G 2018 Adv. Opt. Mater. 6 1701152 Google Scholar
[8]	Huang C Y, Chang H C 2019 IEEE Photon. J. 11 4800208 Google Scholar
[9]	Li G Z, Hu H J, Wu L 2019 Phys. Chem. Chem. Phys. 21 7654 Google Scholar
[10]	Wu C, Khanikaev A B, Shvets G 2011 Phys. Rev. Lett. 106 107403 Google Scholar
[11]	Chang W S, Lassiter J B, Swanglap P, Sobhani H, Khatua S, Nordlander P, Halas N J, Link S 2012 Nano Lett. 12 4977 Google Scholar
[12]	Yu Y, Xue W, Semenova E, Yvind K, Mork J 2017 Nat. Photon. 11 81 Google Scholar
[13]	Hu H J, Zhang F W, Li G Z, Chen J Y, Li Q, Wu L J 2018 Photon. Res. 6 204 Google Scholar
[14]	Yang Z J, Hao Z H, Lin H Q, Wang Q Q 2014 Nanoscale 6 4985 Google Scholar
[15]	黄运欢, 李璞 2015 64 207301 Google Scholar Huang Y H, Li P 2015 Acta Phys. Sin. 64 207301 Google Scholar
[16]	Zhang Y, Jia T Q, Zhang H M, Xu Z Z 2012 Opt. Lett. 37 4919 Google Scholar
[17]	Fu Y H, Zhang J B, Yu Y F, Lukyanchuk B 2012 ACS Nano 6 5130 Google Scholar
[18]	Zhao W, Jiang Y 2015 Opt. Lett. 40 93 Google Scholar
[19]	Yang Z J, Wang Q Q, Lin H Q 2013 Appl. Phys. Lett. 103 111115 Google Scholar
[20]	Zhang S, Genov D A, Wang Y, Liu M, Zhang X 2008 Phys. Rev. Lett. 101 047401 Google Scholar
[21]	Wang J, Liu X, Li L, He J, Fan C, Tian Y, Ding P, Chen D, Xue Q, Liang E 2013 J. Opt. 15 105003 Google Scholar
[22]	Dong Z G, Liu H, Xu M X, Li Tao, Wang S M, Zhu S N, Zhang X 2010 Opt. Express 18 18229 Google Scholar
[23]	Jin X R, Park J, Zheng H, Lee S, Lee Y, Rhee J Y, Kim K W, Cheong H S, Jang W H 2011 Opt. Express 19 21652 Google Scholar
[24]	Bozhevolnyi S I, Evlyukhin A B, Pors A, Nielsen M G, Willatzen M, Albrektsen O 2011 New J. Phys. 13 023034 Google Scholar
[25]	Yang Z J, Zhang Z S, Zhang L H, Li Q Q, Hao Z H, Wang Q Q 2011 Opt. Lett. 36 1542 Google Scholar
[26]	Kai G, Zhang Y L, Qian C, Fung K H 2018 Opt. Express 26 11984 Google Scholar
[27]	Liu G D, Zhai X, Wang L L, Wang B X, Lin Q, Shang X J 2016 Plasmonics 11 381 Google Scholar
[28]	Liu S D, Leong E S P, Li G C, Hou Y, Deng J, Teng J H, Ong H C, Lei D Y 2016 ACS Nano 10 1442 Google Scholar
[29]	Wang J, Fan C, He J, Ding P, Liang E, Xue Q 2013 Opt. Express 21 2236 Google Scholar
[30]	Li G, Li Q, Xu L, Wu L 2015 Plasmonics 10 1401 Google Scholar
[31]	丛超, 吴大建, 刘晓峻 2011 60 046102 Google Scholar Cong C, Wu D J, Liu X J 2011 Acta Phys. Sin. 60 046102 Google Scholar
[32]	Taflove A, Hagness S 2000 Computational Electrodynamics: the Finite-Difference Time-Domain Method (Vol. 2) (Boston: Artech House) pp75−85
[33]	Johnson P B, Christy R W 1972 Phys. Rev. B 6 4370 Google Scholar
[34]	Halas N J, Lal S, Chang W S, Nordlander P 2011 Chem. Rev. 111 3913 Google Scholar
[35]	Feng R, Qiu J, Liu L, Ding W, Chen L 2014 Opt. Express 22 A1713 Google Scholar
[36]	Hu X, Huang Y, Yuan S, Liu Y, Jiao Z, Wang Y, Huang Q, Yu J, Xia J 2015 Plasmonics 10 1817 Google Scholar

[1]	Chen Zhao, Ma Xin-Xin, Li Tong, Wang Yi-Lin. Optical pressure sensor based on Fano resonance in a coupled resonator system. Acta Physica Sinica, 2024, 73(8): 084205. doi: 10.7498/aps.73.20232025
[2]	Yang Qi-Li, Zhang Xing-Fang, Liu Feng-Shou, Yan Xin, Liang Lan-Ju. Multiple Fano resonances in gold split ring disk dimers. Acta Physica Sinica, 2022, 71(2): 027802. doi: 10.7498/aps.71.20210855
[3]	Lu Li-Dan, Zhu Lian-Qing, Zeng Zhou-Mo, Cui Yi-Ping, Zhang Dong-Liang, Yuan Pei. Progress of silicon photonic devices-based Fano resonance. Acta Physica Sinica, 2021, 70(3): 034204. doi: 10.7498/aps.70.20200550
[4]	. Diffraction-induced quadrupolar lattice plasmon modes of high-quality factors for silver nanoparticle arrays. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20211629
[5]	Hu Bao-Jing, Huang Ming, Li Peng, Yang Jing-Jing. Plasmon-induced transparency based on black phosphorus nanorods hybrid model. Acta Physica Sinica, 2021, 70(4): 044201. doi: 10.7498/aps.70.20201331
[6]	. Multiple Fano resonances in gold split ring disk dimers. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20210855
[7]	Hu Bao-Jing, Huang Ming, Li Peng, Yang Jing-Jing. Multiband plasmon-induced transparency based on nanometals-graphene hybrid model. Acta Physica Sinica, 2020, 69(17): 174201. doi: 10.7498/aps.69.20200200
[8]	Hu Bao-Jing, Huang Ming, Li Peng, Yang Cheng-Fu. Multiband plasmon-induced transparency based on silver nanorods and nanodisk hybrid model. Acta Physica Sinica, 2020, 69(13): 134202. doi: 10.7498/aps.69.20200093
[9]	Chen Ying, Cao Jing-Gang, Xie Jin-Chao, Gao Xin-Bei, Xu Yang-Mei, Li Shao-Hua. Resonance characteristics of independently tuned dual Fano of metal-dielectric-metal waveguide coupling square cavity with double baffles. Acta Physica Sinica, 2019, 68(10): 107302. doi: 10.7498/aps.68.20181985
[10]	Zhang Xing-Fang, Liu Feng-Shou, Yan Xin, Liang Lan-Ju, Wei De-Quan. Double Fano resonance in gold nanotube embedded with a concentric elliptical cylinder. Acta Physica Sinica, 2019, 68(6): 067301. doi: 10.7498/aps.68.20182249
[11]	Cui Hong-Fei, Li Kai, Yang Chen-Guang, He Shu-Li. Magnetic properties of (Fe1-xCox)3BO5 nanorods. Acta Physica Sinica, 2015, 64(5): 057501. doi: 10.7498/aps.64.057501
[12]	Xu Tian-Ning, Li Xiang, Jia Wen-Wang, Sui Cheng-Hua, Wu Hui-Zhen. Localized surface plasmon resonance modes in Ag nanowires with pentagonal cross sections. Acta Physica Sinica, 2015, 64(24): 245201. doi: 10.7498/aps.64.245201
[13]	Hua Yun-Feng, Zhang Dong, Zhang Lin-Xi. Ordered structures of nanorods induced by the helixes of semiflexible polymer chains. Acta Physica Sinica, 2015, 64(8): 088201. doi: 10.7498/aps.64.088201
[14]	Zhang Wen-Ping, Ma Zhong-Yuan, Xu Jun, Xu Ling, Li Wei, Chen Kun-Ji, Huang Xin-Fan, Feng Duan. Simulation of localized surface plasmon resonance of hexagonal Ag nanoarrays and amorphous oxidized silicon nitride. Acta Physica Sinica, 2015, 64(17): 177301. doi: 10.7498/aps.64.177301
[15]	Zhu Xiao-Min, Ren Xin-Cheng, Guo Li-Xin. Study on wide-band scattering from rectangular cross-section above rough land surface with exponential type distribution using FDTD. Acta Physica Sinica, 2014, 63(5): 054101. doi: 10.7498/aps.63.054101
[16]	Liu Jian-Xiao, Zhang Jun-Liang, Su Ming-Min. Finite-difference time domain method for the analysis of radar scattering characteristic of metal target coated with anisotropic ferrite. Acta Physica Sinica, 2014, 63(13): 137501. doi: 10.7498/aps.63.137501
[17]	Zhang Zhi-Dong, Gao Si-Min, Wang Hui, Wang Hong-Yan. Resonance mode of an equilateral triangle with triangle notch. Acta Physica Sinica, 2014, 63(12): 127301. doi: 10.7498/aps.63.127301
[18]	Wang Pei-Pei, Yang Chao-Jie, Li Jie, Tang Peng, Lin Feng, Zhu Xing. Polarization properties of plasmonic color filters comprised of arrays of subwavelength size holes on Au films. Acta Physica Sinica, 2013, 62(16): 167302. doi: 10.7498/aps.62.167302
[19]	Ren Xin-Cheng, Guo Li-Xin, Jiao Yong-Chang. Investigation of electromagnetic scattering interaction between the column with rectangular cross-section and rough land surface covered with snow using finite difference time domain method. Acta Physica Sinica, 2012, 61(14): 144101. doi: 10.7498/aps.61.144101
[20]	Shao Zheng-Zheng, Wang Xiao-Feng, Zhang Xue-Ao, Chang Sheng-Li. Piezoelectric discharge characteristic of ZnO nanorod studied with atomic force microscopy. Acta Physica Sinica, 2010, 59(1): 550-554. doi: 10.7498/aps.59.550

Catalog

Vol. 68, Issue 19 - 2019-10-05

Metrics

Abstract views: 9130
PDF Downloads: 115
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板