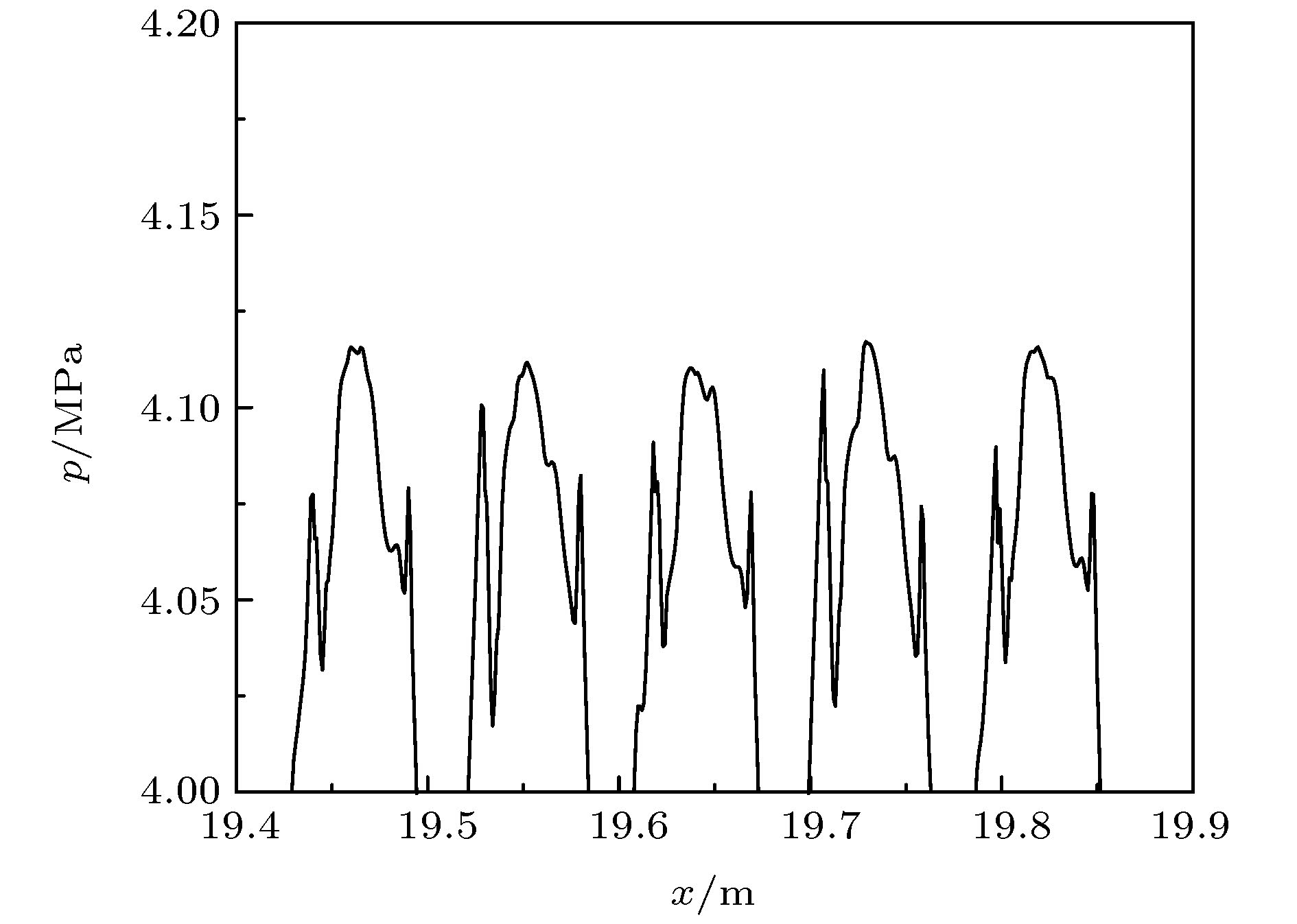
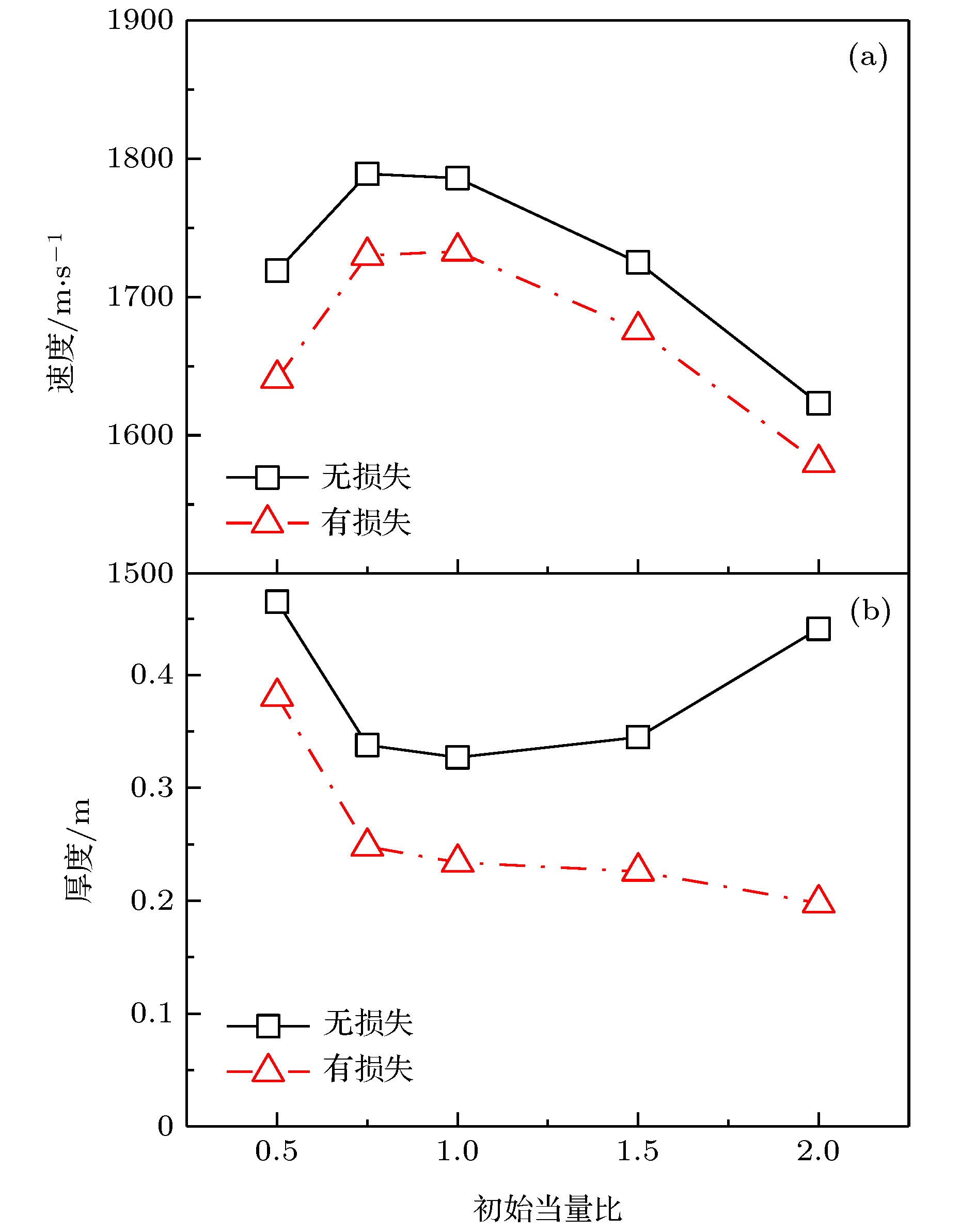
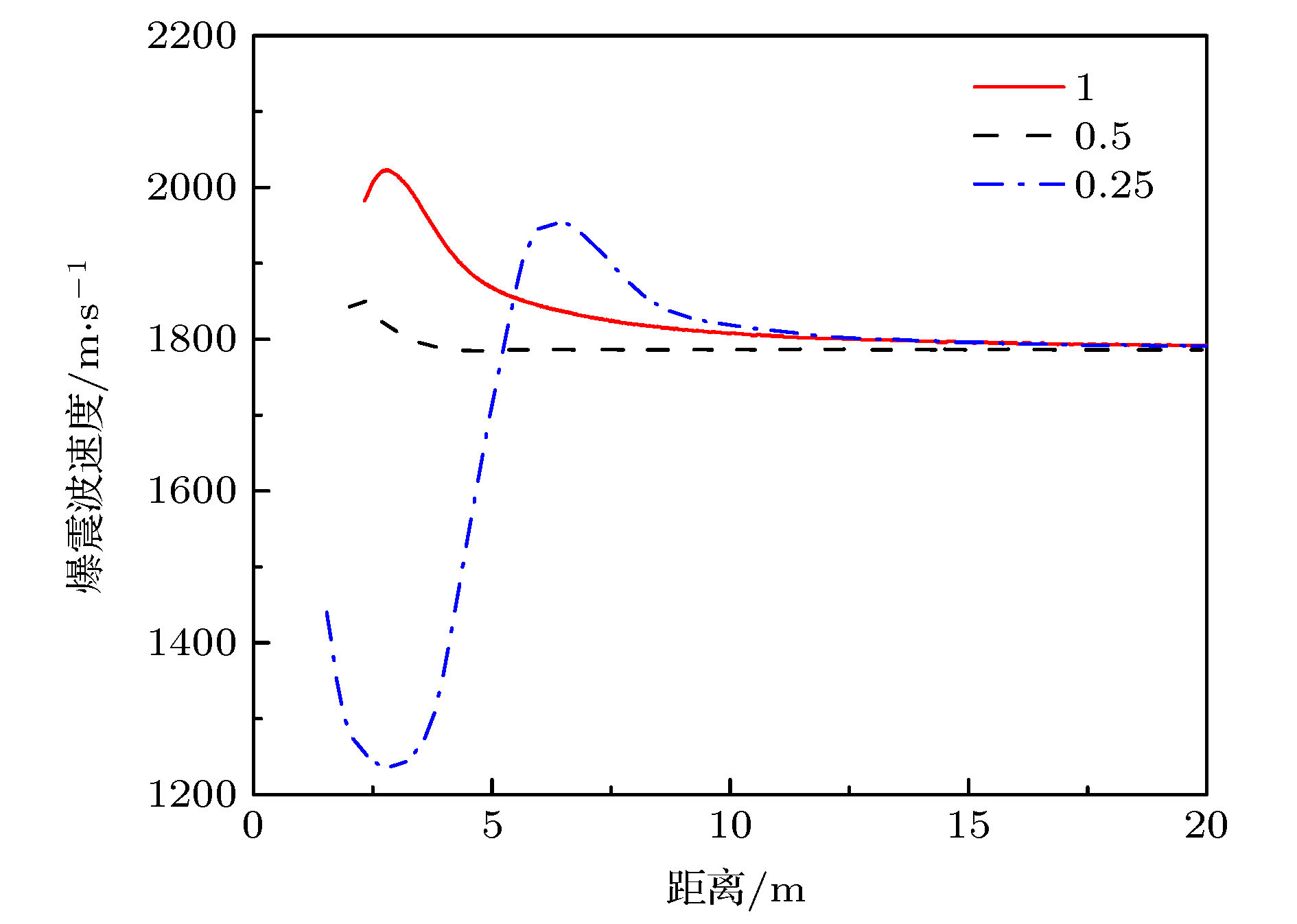
-
In this paper, a one-dimensional unsteady model is established for the detonation of magnesium particle-air mixture. Through numerical simulation, the influences of the loss caused by the side wall of the detonation tube, the diameter of the magnesium particles, the initial equivalent ratio of the magnesium particles, and the deposition process on the surface of the particles, and the ignition energy on the structure and development of the detonation wave and the distribution of the flow field parameters inside the detonation wave are obtained. The studies show that there appear oscillations during the propagation of the fully developed one-dimensional unsteady detonation wave of magnesium particle-air mixture, but the amplitude is less than 1 m/s. Considering the loss of the wall, the pressure and temperature inside the detonation wave decrease with the inner diameter of the detonation tube decreasing, thus leading the propagation velocity and the thickness of the detonation wave decreasing. In the case without the wall loss, as the initial particle size increases, the detonation wave velocity remains unchanged, and the detonation wave thickness monotonically increases. With the wall loss taken into consideration, the stable velocity and thickness of detonation wave are lower than without considering the wall loss under the same initial conditions. Both the difference between the velocities and the difference between thickness values under the conditions with and without considering the wall loss increase as initial particle size increases. The detonation wave thickness with a double-size-distribution initial particle size is more than that with an equivalent single-size-distribution. Meanwhile the stable propagation velocity of the former is less than that of the latter. In the range of initial particle equivalent ratio of 0.5–2, as the initial equivalent ratio increases, the stable velocity of ideal detonation wave first increases and then decreases, and the thickness of the detonation wave first decreases and then increases. Considering the loss of the wall, with the increase of the initial equivalence ratio, the stable velocity of detonation wave first decreases and then increases and the thickness of the detonation wave monotonically decreases. When the initial equivalence ratio of the initial particles is in a lower range (0.337–0.382), the melting of MgO occurs near the CJ plane. As a result, the melting process of MgO has no significant effect on the stability of the detonation wave propagation, but has a greater influence on the structure of the detonation wave: when the initial equivalence ratio is lower in the above range, MgO in the detonation wave is partially melted and then re-solidified. When the initial equivalence ratio is higher in the above range, the MgO at the CJ plane is still in the melting process, and there is a low-strength secondary compression process in the detonation wave. Considering the fact that the combustion products are deposited on the particle surface, the detonation wave velocity increases while the corresponding thickness of the detonation wave remains almost unchanged with the increase of the deposition rate. The parameters of the ignition region have no influence on the final stable propagation state of the detonation wave, but will affect the development process of the detonation wave. Selecting appropriate paraneters of ignition zone can shorten the distance of denotation wave reaching to the steady propagation.
-
Keywords:
- heterogeneous detonation /
- magnesium particle fuel /
- surface deposition /
- energy loss caused by wall
[1] Veyssiere B, Ingignoli W 2003 Shock Waves 12 291
Google Scholar
[2] Palaszewski B, Jurns J, Breisacher K, Kearns K 2004 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit Fort Lauderdale, USA, July 11–14, 2004 p4191
[3] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov, Yu A 2010 Dokl. Phys. 55 142
Google Scholar
[4] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2011 Combust. Explo. Shock. 47 473
Google Scholar
[5] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2012 Combust. Explo. Shock. 48 203
Google Scholar
[6] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2013 Combust. Explo. Shock. 49 705
Google Scholar
[7] Bykovskii F A, Zhdan S A, Vedernikov E F 2014 Combust. Explo. Shock. 50 214
Google Scholar
[8] 刘龙, 夏智勋, 黄利亚, 马立坤, 那旭东 2019 68 244701
Google Scholar
Liu L, Xia Z X, Huang L Y, Ma L K, Na X D 2019 Acta Phys. Sin. 68 244701
Google Scholar
[9] Gosteev Y A, Fedorov A V 2005 Combust. Expl. Shock Waves 41 190
Google Scholar
[10] Zhang F. 2009 Shock Wave Science and Technology Reference Library (Vol.4) (Berlin, Heidelberg: Springer) pp99, 153, 159
[11] Cassel H M, Liebman I 1962 Combust. Flame. 6 153
Google Scholar
[12] 洪滔, 秦承森 1999 爆炸与冲击 19 335
Google Scholar
Hong T, Qing C S 1999 Expl. Shock Wave 19 335
Google Scholar
[13] Derevyaga M E, Stesik L N, Fedorin E A 1978 Combust. Explo. Shock. 5 3
[14] 冯运超 2014 硕士学位论文(长沙: 国防科学技术大学)
Feng Y C 2014 Master Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[15] Pilling N B, Bedworth R E 1923 Journal Inst. Met 29 529
[16] Ezhovskii G K, Ozerov E S 1977 Combust. Explo. Shock. 13 716
Google Scholar
[17] Ezhovskii G K, Ozerov E S, Roshchenya Y V 1979 Combust. Explo. Shock. 15 194
Google Scholar
[18] Bloshenko V N, Merzhanov A G, Khaikin B I 1976 Combust. Explo. Shock. 12 612
Google Scholar
[19] Valov A E, Gusachenko E I, Shevtsov V I 1991 Combust. Explo. Shock. 27 393
Google Scholar
[20] 洪滔, 秦承森 2004 爆炸与冲击 24 193
Google Scholar
Hong T, Qing C S 2004 Expl. Shock Wave 24 193
Google Scholar
[21] Lee J H S 1998 The Detonation Phenomenon (New York:Cambridge University Press) p108
[22] Steinberg T A, Wilson D, Benz F 1992 Combust. Flame 91 200
Google Scholar
[23] 杨晋朝 2013 博士学位论文(长沙: 国防科学技术大学)
Yang J C 2013 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[24] 杨涛, 方丁酉, 唐乾刚 2008 火箭发动机燃烧原理 (长沙: 国防科技大学出版社)
Yang T, Fang D J, Tang Q G 2008 Combustion Principle of Rocket Engine (Changsha: National Defense Science and Technology University Press) (in Chinese)
[25] Abbud-Madrid A, Modak A, Branch M C 2001 J. Propul. Power 17 852
Google Scholar
[26] Fox T W, Rackett C W, Nicholls J A 1978 Proceedings of the 11th International Symposium on Shock Waves and Tubes, Seattle, USA, July 11–14, 1978 p262
[27] 韦伟, 翁春生 2017 固体火箭技术 40 41
Wei W, Wen C S 2017 J. Solid Rock. Technol. 40 41
[28] 潘啸, 翁春生 2017 南京理工大学学报(自然科学版) 41 1
Pan X, Weng C H 2017 J. Nanjing Univ. Sci. Technol. 41 1
[29] 杨晋朝, 夏智勋, 胡建新 2013 62 074701
Google Scholar
Yang J C, Xia Z X, Hu J X 2013 Acta Phys. Sin. 62 074701
Google Scholar
[30] Fedorov A V, Khmel’ T A 1999 Combust. Expl. Shock Waves 9 313
[31] Zhang F, Grönig H, Van de Ven A 2001 Shock Waves 11 53
Google Scholar
[32] Li Y, Alexander C G, Wolanski P, Kauffman C W, Sichel M 1993 13 th International Colloquium on Dynamics of Explosions and Reactive Systems Nagoya, Japan, July 28–August 2, 1991 p170
[33] Tulis A J, Selman J R 1982 19th Symposium (International) on Combustion, The Combustion Institute, Haifa, Israel, August 8–13 1982 p655
[34] 刘庆明, 范宝春, 陈志华, 李鸿志 1997 实验力学 12 376
Liu Q M, Fan B C, Chen Z H, Li H Z 1997 J. Exp. Mech. 12 376
-
图 1 不同网格尺度对应的压力分布
Figure 1. Spatial distribution of the gas-phase pressure with different grid sizes.
图 2 不同时刻爆震波压力峰附近的压力分布
Figure 2. Pressure distribution near peak at different time.
图 3 不同燃烧模型对应的爆震波内流场参数分布 (a) 密度和浓度; (b) 速度; (c) 温度; (d) 压力
Figure 3. Parameters distribution in detonation wave with different combustion models: (a) Density and concentration; (b) velocity; (c) temperature; (d) pressure.
图 4 在
${f_{\rm{S}} } = 1.1$ 时对应的稳定传播状态爆震波两相温度分布Figure 4. Temperature distribution of gas and particle phases inside steady detonation wave with
${f_{\rm{S}} } = 1.1$ .
图 5 爆震波参数随
${f_{\rm{S}} }$ 的变化 (a) 爆震波厚度; (b) CJ面两相温度; (c) CJ面颗粒相浓度; (d) 爆震波速度Figure 5. Variation of detonation parameters with different value of
${f_{\rm{S}} }$ : (a) Thickness; (b) temperature at CJ plane; (c) particle concentration at CJ plane; (d) velocity
图 6 不同管径条件下爆震波内的压力和气相温度分布 (a) 压力; (b) 气相温度
Figure 6. Pressure and gas-phase temperature distribution inside detonation wave with different tube inner-diameters: (a) Pressure; (b) gas-phase temperature.
图 7 稳定传播的爆震波速度和爆震波厚度随初始当量比的变化 (a) 速度; (b) 厚度
Figure 7. Variation of steady velocity and thickness of detonation wave with different initial equivalent ratio: (a) Velocity; (b) thickness.
图 8 不同当量比条件下爆震波内气相密度分布
Figure 8. Gas-phase density distribution inside detonation wave with different initial equivalent ratio.
图 9 不同初始当量比条件下爆震波内参数分布 (a)压力; (b)温度
Figure 9. Parameters distribution inside detonation wave with different initial equivalent ratio: (a) Pressure; (b) temperature.
图 10 不同初始当量比条件下不同位置处的爆震波压力峰值
Figure 10. Pressure peak at different position with different initial equivalent ratio.
图 11 不同点火区长度对应的爆震波速度发展过程
Figure 11. Development of detonation wave velocity with different length of ignition zone.
图 12 不同点火区参数对应的爆震波速度发展过程
Figure 12. Development of detonation wave velocity with different field parameters of ignition zone.
表 1 不同模型对应的爆震波稳定速度和厚度
Table 1. Steady velocity and thickness of detonation wave with different models.
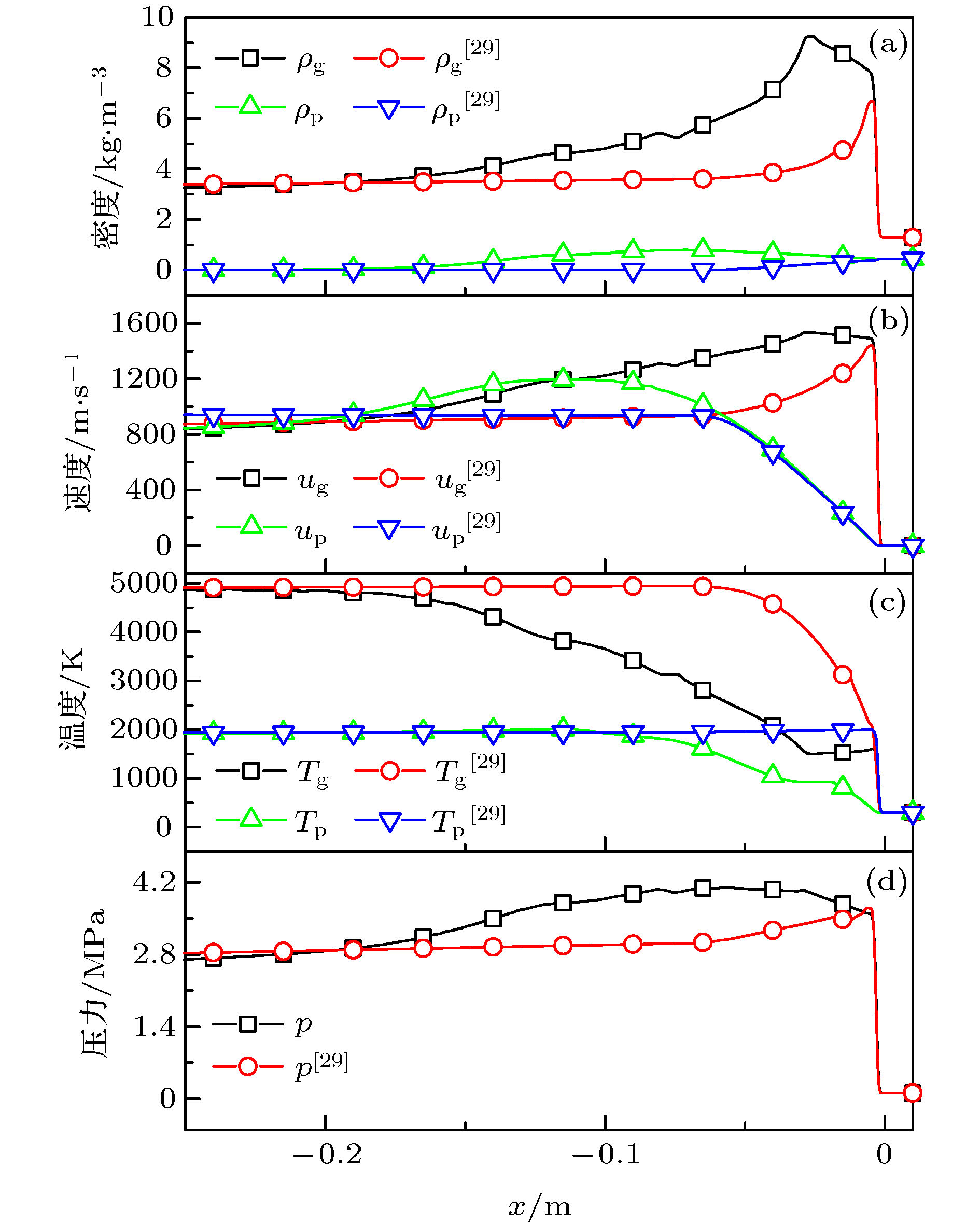
参数 本文模型 文献[29]模型 两相ZND模型 爆震波速度/(m·s–1) 1786 1789 1782.28 爆震波厚度/m 0.327 0.055 0.331 
DownLoad: CSV
表 2 不同爆震管内径条件下爆震波稳定传播速度、厚度和rCJ/r0
Table 2. Steady velocity, thickness and rCJ/r0 at CJ plane of detonation wave with different tube inner-diameters.
管径 $\infty $ 1 m 0.3 m 0.15 m 0.075 m 稳定速度/(m·s–1) 1786 1777.5 1758.5 1733 1691.5 爆震波厚度/m 0.327 0.297 0.254 0.234 0.2185 CJ面rCJ/r0 < 0.1 0.162 0.199 0.239 0.277 注: 管径$\infty $表示不考虑管壁损失的理想条件
DownLoad: CSV
表 3 不同颗粒初始粒径对应的爆震波传播速度和厚度
Table 3. Steady velocity and thickness of detonation wave with different initial particle diameter.
粒径 5 μm 10 μma 10 μmb 15 μm 20 μm 爆震波速度/(m·s–1) 无损失 1786 1786 1786 1786 1786 有损失 1762 1733 1700 1702 1662 爆震波厚度/m 无损失 0.171 0.327 0.622 0.614 0.908 有损失 0.099 0.234 0.446 0.425 0.666 注: a, 单一粒径; b, 5 μm和15 μm掺混后的平均粒径.
DownLoad: CSV
-
[1] Veyssiere B, Ingignoli W 2003 Shock Waves 12 291
Google Scholar
[2] Palaszewski B, Jurns J, Breisacher K, Kearns K 2004 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit Fort Lauderdale, USA, July 11–14, 2004 p4191
[3] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov, Yu A 2010 Dokl. Phys. 55 142
Google Scholar
[4] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2011 Combust. Explo. Shock. 47 473
Google Scholar
[5] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2012 Combust. Explo. Shock. 48 203
Google Scholar
[6] Bykovskii F A, Zhdan S A, Vedernikov E F, Zholobov Yu A 2013 Combust. Explo. Shock. 49 705
Google Scholar
[7] Bykovskii F A, Zhdan S A, Vedernikov E F 2014 Combust. Explo. Shock. 50 214
Google Scholar
[8] 刘龙, 夏智勋, 黄利亚, 马立坤, 那旭东 2019 68 244701
Google Scholar
Liu L, Xia Z X, Huang L Y, Ma L K, Na X D 2019 Acta Phys. Sin. 68 244701
Google Scholar
[9] Gosteev Y A, Fedorov A V 2005 Combust. Expl. Shock Waves 41 190
Google Scholar
[10] Zhang F. 2009 Shock Wave Science and Technology Reference Library (Vol.4) (Berlin, Heidelberg: Springer) pp99, 153, 159
[11] Cassel H M, Liebman I 1962 Combust. Flame. 6 153
Google Scholar
[12] 洪滔, 秦承森 1999 爆炸与冲击 19 335
Google Scholar
Hong T, Qing C S 1999 Expl. Shock Wave 19 335
Google Scholar
[13] Derevyaga M E, Stesik L N, Fedorin E A 1978 Combust. Explo. Shock. 5 3
[14] 冯运超 2014 硕士学位论文(长沙: 国防科学技术大学)
Feng Y C 2014 Master Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[15] Pilling N B, Bedworth R E 1923 Journal Inst. Met 29 529
[16] Ezhovskii G K, Ozerov E S 1977 Combust. Explo. Shock. 13 716
Google Scholar
[17] Ezhovskii G K, Ozerov E S, Roshchenya Y V 1979 Combust. Explo. Shock. 15 194
Google Scholar
[18] Bloshenko V N, Merzhanov A G, Khaikin B I 1976 Combust. Explo. Shock. 12 612
Google Scholar
[19] Valov A E, Gusachenko E I, Shevtsov V I 1991 Combust. Explo. Shock. 27 393
Google Scholar
[20] 洪滔, 秦承森 2004 爆炸与冲击 24 193
Google Scholar
Hong T, Qing C S 2004 Expl. Shock Wave 24 193
Google Scholar
[21] Lee J H S 1998 The Detonation Phenomenon (New York:Cambridge University Press) p108
[22] Steinberg T A, Wilson D, Benz F 1992 Combust. Flame 91 200
Google Scholar
[23] 杨晋朝 2013 博士学位论文(长沙: 国防科学技术大学)
Yang J C 2013 Ph. D. Dissertation (Changsha: National University of Defense Technology) (in Chinese)
[24] 杨涛, 方丁酉, 唐乾刚 2008 火箭发动机燃烧原理 (长沙: 国防科技大学出版社)
Yang T, Fang D J, Tang Q G 2008 Combustion Principle of Rocket Engine (Changsha: National Defense Science and Technology University Press) (in Chinese)
[25] Abbud-Madrid A, Modak A, Branch M C 2001 J. Propul. Power 17 852
Google Scholar
[26] Fox T W, Rackett C W, Nicholls J A 1978 Proceedings of the 11th International Symposium on Shock Waves and Tubes, Seattle, USA, July 11–14, 1978 p262
[27] 韦伟, 翁春生 2017 固体火箭技术 40 41
Wei W, Wen C S 2017 J. Solid Rock. Technol. 40 41
[28] 潘啸, 翁春生 2017 南京理工大学学报(自然科学版) 41 1
Pan X, Weng C H 2017 J. Nanjing Univ. Sci. Technol. 41 1
[29] 杨晋朝, 夏智勋, 胡建新 2013 62 074701
Google Scholar
Yang J C, Xia Z X, Hu J X 2013 Acta Phys. Sin. 62 074701
Google Scholar
[30] Fedorov A V, Khmel’ T A 1999 Combust. Expl. Shock Waves 9 313
[31] Zhang F, Grönig H, Van de Ven A 2001 Shock Waves 11 53
Google Scholar
[32] Li Y, Alexander C G, Wolanski P, Kauffman C W, Sichel M 1993 13 th International Colloquium on Dynamics of Explosions and Reactive Systems Nagoya, Japan, July 28–August 2, 1991 p170
[33] Tulis A J, Selman J R 1982 19th Symposium (International) on Combustion, The Combustion Institute, Haifa, Israel, August 8–13 1982 p655
[34] 刘庆明, 范宝春, 陈志华, 李鸿志 1997 实验力学 12 376
Liu Q M, Fan B C, Chen Z H, Li H Z 1997 J. Exp. Mech. 12 376
DownLoad:
Catalog
Metrics
- Abstract views: 5203
- PDF Downloads: 71
- Cited By: 0
