-
In recent years, exploring new topological quantum model structures and in depth analyzing the novel physical properties in various multimerized topological lattices have become a hot topic in the field of quantum optics. Among the different model structures, the multimerized non-Hermitian lattice controlled by different parameters in the future research of topological quantum materials, we believe, can exhibit more meaningful novel topological properties. As one of the most classic topological models, the one-dimensional Aubry-André-Harper (AAH) model has received more and more attention in the study of multimerized lattices. In this paper, we focus on the novel topological properties of a trimerized non-Hermitian lattice, and extend the trimer model structure from a one-dimensional chain to a quasi-one-dimensional zigzag structure. The results show that firstly, if the nearest-neighbor forward coupling coefficient in the unit cell is not equal to the backward coupling coefficient, the chiral inversion symmetry of the system is destroyed. It can be observed that the bulk states and the edge states in the trimerization model will be localized on the same edge of the lattice, and the skin effect will appear in the system. With the increase of the nearest-neighbor coupling coefficient, the width of the edge state changes in which the lower edge state of the imaginary part of the spectrum is narrowed until it disappears. The degree of degeneracy of the system changes, and the number of edge states is reduced from four to two. Remarkably, the generalized bulk-boundary correspondence is shown in certain non-Hermitian topological systems. Secondly, when the trimerization model considers the influence of the next-nearest-neighbor coupling, the numerical results show that the upper and lower energy gaps in the energy spectrum and the edge states in the energy spectrum are asymmetrical as the next-nearest-neighbor coupling coefficient is modulated in an appropriate range. The upper energy gaps and the edge states are narrowed, and the edge states of the lower energy gaps are widened. At the same time, the novel topology features of the system can also be used to achieve the quantitative control of the energy spectrum edge states, and other interesting directions are worth exploring.
-
Keywords:
- edge states /
- topological insulators /
- skin effect
[1] Klitzing K, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Klitzing K 1986 Rev. Mod. Phys. 58 519
Google Scholar
[3] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[4] Haldane F D M, Raghu S 2008 Phys. Rev. Lett. 100 013904
Google Scholar
[5] Raghu S, Haldane F D M 2008 Phys. Rev. A 78 033834
Google Scholar
[6] Chang C Z, Zhang J S, Feng X, Xue Q K 2013 Sci. Rep. 340 6129
[7] Goldman N, Budich J C, Zoller P 2016 Nat. Phys. 12 639
Google Scholar
[8] 孙晓晨, 何程, 卢明辉, 陈延峰 2017 22 224203
Google Scholar
Sun X C, He C, Lu M H, Chen Y F 2017 Acta Phys. Sin. 22 224203
Google Scholar
[9] 张卫锋, 李春艳, 陈险锋, 黄长明, 叶芳伟 2017 22 220201
Google Scholar
Zhang W F, Li C Y, Chen X F, Huang C M, Ye F W 2017 Acta Phys. Sin. 22 220201
Google Scholar
[10] 陈西浩, 王秀娟 2018 19 190301
Google Scholar
Chen X H, Wang X J 2018 Acta Phys. Sin. 19 190301
Google Scholar
[11] Aubry S, Andreé G, Isr A 1980 Phys. Soc. 322 235
[12] harper P G 1955 Proc. Phys. Soc. London Sect. A 68 874
Google Scholar
[13] Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Silberberg Y 2009 Phys. Rev. Lett. 103 013901
Google Scholar
[14] Biddle J, Wang B, Priour D J, Sarma S D 2009 Phys. Rev. A 80 021603 (R)
Google Scholar
[15] Ganeshan S, Sun K, Sarma S D 2013 Phys. Rev. Lett. 110 180403
Google Scholar
[16] Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651
Google Scholar
[17] Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384
Google Scholar
[18] Yurkevich I V, Lerner I V 1999 Phys. Rev. Lett. 82 5080
Google Scholar
[19] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[20] Dorey P, Dunning C, Tateo R 2001 J. Phys. A 34 5679
Google Scholar
[21] Mostafazadeh A 2002 J. Math. Phys. 43 205
Google Scholar
[22] Jones H F 2005 J. Phys. A 38 1741
Google Scholar
[23] Klaiman S, Günther U, Moiseyev N 2008 Phys. Rev. Lett. 101 080402
Google Scholar
[24] Znojil M 2008 Phys. Rev. D 78 025026
Google Scholar
[25] Jin L, Song Z 2009 Phys. Rev. A 80 052107
Google Scholar
[26] Rotter I 2009 J. Phys. A: Math. Theor. 42 124206
[27] Moiseyev N 2011 Non-Hermitian Quantum Mechanics (Cambridge: Cambridge University) pp 211—247
[28] Joqlekar Y N, Barnett J L 2011 Phys. Rev. A 84 024103
Google Scholar
[29] Longhi S, Valle G D 2012 Phys. Rev. A 85 012112
Google Scholar
[30] Longhi S 2013 Phys. Rev. A 88 052102
Google Scholar
[31] Longhi S 2016 Phys. Rev. A 94 022102
Google Scholar
[32] Jin L, Xin F 2017 Phys. Rev. A 97 012121
[33] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[34] Xing Y, Qi L, Cao J, Wang D Y, Bai C H, Wang H F, Zhu A D, Zhang S 2017 Phys. Rev. A 96 043810
Google Scholar
[35] Zhou Y H, Shen H Z, Zhang X Y, Yi X X 2018 Phys. Rev. A 97 043819
Google Scholar
[36] Schomerus H, Wiersig J 2014 Phys. Rev. A 90 053819
Google Scholar
[37] Cheng Q, Pan Y, Wang Q, Li T, Zhu S 2015 Laser Photonics Rev. 9 392
Google Scholar
[38] Longhi S, Gatti D, Della Valle G 2015 Phys. Rev. B 92 094204
Google Scholar
[39] Martinez Alvarez V M, Barrios Vargas J E, Foa Torres L E F 2018 Phys. Rev. B 97 121401(R)
Google Scholar
[40] Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[41] Jin L 2017 Phys. Rev. A 96 032103
Google Scholar
-
图 1 扩展的三聚化非厄密晶格示意图
Figure 1. Schematic of the generalized trimerized non-Hermitian lattice.
图 2 三聚化非厄密晶格的本征能谱 (a), (c), (e)和(g)分别为
$\mu=0, 0.1, 0.15, 0.2$ 时本征能谱的实部; (b), (d), (f)和(h)分别为$\mu=0, 0.1, 0.15, 0.2$ 时本征能谱的虚部, 边缘态能带用绿色实线和棕色虚线表示Figure 2. The eigen-energy spectrum of the trimerized non-Hermitian lattice. (a), (c), (e) and (g) show the real parts of the energy spectrum for
$\mu=0, 0.1, 0.15, 0.2$ , respectively; (b), (d), (f) and (h) show the imaginary parts of the energy spectrum for$\mu=0, 0.1, 0.15, 0.2$ . Green solid lines and brown dash lines represent the energy band of the edge states.
图 3 系统本征态的光子分布 (a)
$\mu=0$ ; (b)$\mu=0.1$ ; (c)$\mu=0.2$ ; (d)$\mu=0.3$ Figure 3. Photon distributions for eigenstates of the system: (a)
$\mu=0$ ; (b)$\mu=0.1$ ; (c)$\mu=0.2$ ; (d)$\mu=0.3$ .
图 4 次近邻耦合影响下系统的本征能谱和边缘态的光子分布 (a), (d)和(g)分别为
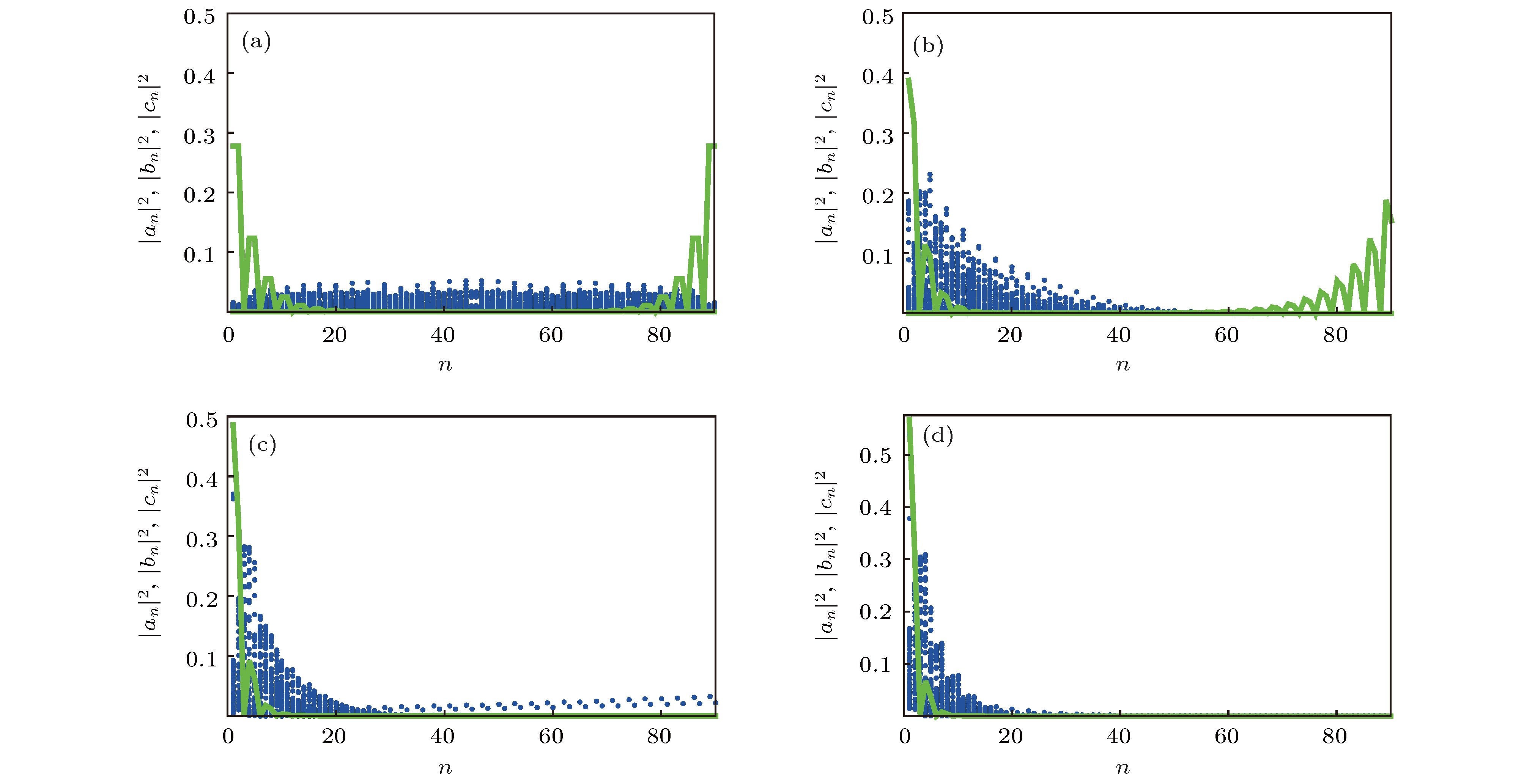
$\nu=0.1, 0.15, 0.2$ 时本征能谱的实部; (b), (e)和(h)分别为$\nu=0.1, 0.15, 0.2$ 时上能隙中的边缘态; (c), (f)和(i)分别为$\nu=0.1, 0.15, 0.2$ 时下能隙的边缘态Figure 4. The eigen-energy spectrum and photon distributions for edge states of the system under the influence of the next-nearest-neighbor coupling: (a), (d) and (g) show the real parts of the energy spectrum for
$\nu=0.1, 0.15, 0.2$ ; (b), (e) and (h) show the edge states whose energy band are in the upper gaps for$\nu=0.1, 0.15, 0.2$ ; (c), (f) and (i) show the edge states whose energy bands are in the lower gaps for$\nu=0.1, 0.15, 0.2$ . -
[1] Klitzing K, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494
Google Scholar
[2] Klitzing K 1986 Rev. Mod. Phys. 58 519
Google Scholar
[3] Haldane F D M 1988 Phys. Rev. Lett. 61 2015
Google Scholar
[4] Haldane F D M, Raghu S 2008 Phys. Rev. Lett. 100 013904
Google Scholar
[5] Raghu S, Haldane F D M 2008 Phys. Rev. A 78 033834
Google Scholar
[6] Chang C Z, Zhang J S, Feng X, Xue Q K 2013 Sci. Rep. 340 6129
[7] Goldman N, Budich J C, Zoller P 2016 Nat. Phys. 12 639
Google Scholar
[8] 孙晓晨, 何程, 卢明辉, 陈延峰 2017 22 224203
Google Scholar
Sun X C, He C, Lu M H, Chen Y F 2017 Acta Phys. Sin. 22 224203
Google Scholar
[9] 张卫锋, 李春艳, 陈险锋, 黄长明, 叶芳伟 2017 22 220201
Google Scholar
Zhang W F, Li C Y, Chen X F, Huang C M, Ye F W 2017 Acta Phys. Sin. 22 220201
Google Scholar
[10] 陈西浩, 王秀娟 2018 19 190301
Google Scholar
Chen X H, Wang X J 2018 Acta Phys. Sin. 19 190301
Google Scholar
[11] Aubry S, Andreé G, Isr A 1980 Phys. Soc. 322 235
[12] harper P G 1955 Proc. Phys. Soc. London Sect. A 68 874
Google Scholar
[13] Lahini Y, Pugatch R, Pozzi F, Sorel M, Morandotti R, Davidson N, Silberberg Y 2009 Phys. Rev. Lett. 103 013901
Google Scholar
[14] Biddle J, Wang B, Priour D J, Sarma S D 2009 Phys. Rev. A 80 021603 (R)
Google Scholar
[15] Ganeshan S, Sun K, Sarma S D 2013 Phys. Rev. Lett. 110 180403
Google Scholar
[16] Hatano N, Nelson D R 1997 Phys. Rev. B 56 8651
Google Scholar
[17] Hatano N, Nelson D R 1998 Phys. Rev. B 58 8384
Google Scholar
[18] Yurkevich I V, Lerner I V 1999 Phys. Rev. Lett. 82 5080
Google Scholar
[19] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[20] Dorey P, Dunning C, Tateo R 2001 J. Phys. A 34 5679
Google Scholar
[21] Mostafazadeh A 2002 J. Math. Phys. 43 205
Google Scholar
[22] Jones H F 2005 J. Phys. A 38 1741
Google Scholar
[23] Klaiman S, Günther U, Moiseyev N 2008 Phys. Rev. Lett. 101 080402
Google Scholar
[24] Znojil M 2008 Phys. Rev. D 78 025026
Google Scholar
[25] Jin L, Song Z 2009 Phys. Rev. A 80 052107
Google Scholar
[26] Rotter I 2009 J. Phys. A: Math. Theor. 42 124206
[27] Moiseyev N 2011 Non-Hermitian Quantum Mechanics (Cambridge: Cambridge University) pp 211—247
[28] Joqlekar Y N, Barnett J L 2011 Phys. Rev. A 84 024103
Google Scholar
[29] Longhi S, Valle G D 2012 Phys. Rev. A 85 012112
Google Scholar
[30] Longhi S 2013 Phys. Rev. A 88 052102
Google Scholar
[31] Longhi S 2016 Phys. Rev. A 94 022102
Google Scholar
[32] Jin L, Xin F 2017 Phys. Rev. A 97 012121
[33] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[34] Xing Y, Qi L, Cao J, Wang D Y, Bai C H, Wang H F, Zhu A D, Zhang S 2017 Phys. Rev. A 96 043810
Google Scholar
[35] Zhou Y H, Shen H Z, Zhang X Y, Yi X X 2018 Phys. Rev. A 97 043819
Google Scholar
[36] Schomerus H, Wiersig J 2014 Phys. Rev. A 90 053819
Google Scholar
[37] Cheng Q, Pan Y, Wang Q, Li T, Zhu S 2015 Laser Photonics Rev. 9 392
Google Scholar
[38] Longhi S, Gatti D, Della Valle G 2015 Phys. Rev. B 92 094204
Google Scholar
[39] Martinez Alvarez V M, Barrios Vargas J E, Foa Torres L E F 2018 Phys. Rev. B 97 121401(R)
Google Scholar
[40] Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[41] Jin L 2017 Phys. Rev. A 96 032103
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8303
- PDF Downloads: 222
- Cited By: 0
