-
提出一种基于超导传输线腔的一维晶格理论方案, 其中包含两种超导微波腔系统. 通过调控磁通量子比特来操纵临近和次临近晶胞之间的相互作用, 使其获得集体动力学演化规律, 来研究其中的拓扑特性. 首先, 分析了奇偶晶格数目的能谱和边缘状态, 发现奇偶晶格数将会影响系统的拓扑特性, 并且边缘状态分布发生翻转过程. 其次, 在次临近的相互作用下, 发现其相互作用存在相互制约现象, 通过调控其相互作用, 可以实现系统拓扑相变和拓扑量子态的传递过程. 最后, 研究了缺陷对拓扑特性的影响, 发现缺陷势能较小时, 系统能带变化周期稳定, 边缘态保持不变, 能谱产生微小波动, 并且可以区分; 缺陷势能较大时, 能带分布被破坏, 将会变得无序和混乱. 根据本文的研究结果, 可以设计一些新型量子器件, 应用在量子光学和量子信息处理中.We propose a theoretical scheme for a one-dimensional lattice based on a superconducting quantum circuit system consisting of two types of superconducting microwave cavities, the interaction between nearest-neighbor and next-nearest-neighbor unit cells that can be adjusted by the magnetic flux, the system can obtain the collective dynamic evolution and study the topological properties of the system.First, we investigate the energy spectrum and edge states of the odd-even lattice size and find that the odd-even lattice number affects the topological properties of the system. Furthermore, considering the next-nearest interactions, it is found that there are constraints on the next-nearest interactions, which can be tuned to study the topological phase transitions of the system and the transfer of topological quantum states.In addition, considering the influence of defects on topological properties, it is found that the defect potential energy is small, the system energy band is stable, the edge states remain unchanged, and the energy spectrum fluctuation is small and distinguishable. Conversely, the energy band distribution is destroyed, it will become disordered and chaotic. The research results can design some new quantum devices for quantum optics and quantum information processing.
-
Keywords:
- quantum optics /
- superconducting quantum circuits /
- topological insulators /
- quantum states
[1] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[2] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[3] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[4] Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys 88 035005
Google Scholar
[5] Xu Z, Zhang Y, Chen S 2017 Phys. Rev. A 96 013606
Google Scholar
[6] Li L, Xu Z, Chen S 2014 Phys. Rev. B 89 085111
Google Scholar
[7] Li L, Chen S 2015 Phys. Rev. B 92 085118
Google Scholar
[8] Mei F, Zhu S L, Zhang Z M, Oh C H, Goldman N 2012 Phys. Rev. A 85 013638
Google Scholar
[9] Xu Z, Zhang R, Chen S, Fu L, Zhang Y 2020 Phys. Rev. A 101 013635
Google Scholar
[10] Wray L A, Xu v, Xia Y, Hsieh D, Fedorov A V, SanHor Y, Cava R J, Bansil A, Lin H, Hasan M Z 2011 Nat. Phys. 7 32
Google Scholar
[11] Malki M, Uhrig G S 2017 Phys. Rev. B 95 235118
Google Scholar
[12] Berg E, Dalla Torre E G, Giamarchi T, Altman E 2008 Phys. Rev. B 77 245119
Google Scholar
[13] Chitov G Y 2018 Phys. Rev. B 97 085131
Google Scholar
[14] Agrapidis C E, van den Brink J, Nishimoto S 2019 Phys. Rev. B 99 224418
Google Scholar
[15] Feng X Y, Zhang G M, Xiang T 2007 Phys. Rev. Lett. 98 087204
Google Scholar
[16] You J Q, Nori F 2011 Nature 474 589
Google Scholar
[17] Devoret M H, Schoelkopf R J 2013 Science 339 1169
Google Scholar
[18] Massel F, Heikkil T T, Pirkkalainen J M, Cho S U, Saloniemi H, Hakonen P J, Sillanpää M A 2011 Nature 480 351
Google Scholar
[19] Teufel J D, Li D, Allman M S, Cicak K, Sirois A J, Whittaker J D, Simmonds R W 2011 Nature 471 204
Google Scholar
[20] Irish E K, Schwab K 2003 Phys. Rev. B 68 155311
Google Scholar
[21] LaHaye M D, Suh J, Echternach P M, Schwab K C, Roukes M L 2009 Nature 459 960
Google Scholar
[22] Wang H F, Zhu A D, Zhang S, Yeon K H 2011 New J. Phys. 13 013021
Google Scholar
[23] Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623
Google Scholar
[24] Blais A, Gambetta J, Wallraff A, Schuster D I, Girvin S M, Devoret M H, Schoelkopf R J 2007 Phys. Rev. A 75 032329
Google Scholar
[25] Ji A C, Sun Q, Xie X C, Liu W M 2009 Phys. Rev. Lett. 102 023602
Google Scholar
[26] Ji A C, Xie X C, Liu W M 2007 Phys. Rev. Lett. 99 183602
Google Scholar
[27] Mei F, Chen G, Tian L, Zhu S L, Jia S 2018 Phys. Rev. A 98 012331
Google Scholar
[28] Mei F, Chen G, Tian L, Zhu S L, Jia S 2018 Phys. Rev. A 98 032323
Google Scholar
[29] Mei F, Xue Z Y, Zhang D W, Tian L, Lee C, Zhu S L 2016 Quantum Sci. Technol. 1 015006
Google Scholar
[30] Zhang Z C, Shao L, Lu W J, Su Y G, Wang Y P, Liu J and Wang X G 2021 Phys. Rev. A 104 053517
Google Scholar
[31] Wang Y P, Zhang Z C, Yu Y F and Zhang Z M 2019 Results Phys. 15 102560
Google Scholar
[32] Koch J, Houck A A, Le Hur K, Girvin S M 2010 Phys. Rev. A 82 043811
Google Scholar
[33] Mei F, You J B, Nie W, Fazio R, Zhu S L, Kwek L C 2015 Phys. Rev. A 92 041805
Google Scholar
[34] Gu F L, Liu J, Mei F, Jia S, Zhang D W, Xue Z Y 2019 npj Quantum Inf. 5 36
[35] Huang Y, Yin Z, Yang W L 2016 Phys. Rev. A 94 022302
Google Scholar
[36] Tan X, Zhao Y, Liu Q, Xue G, Yu H, Wang Z D, Yu Y 2017 npj Quantum Mater. 2 60
Google Scholar
[37] Cao J, Yi X X, Wang H F 2020 Phys. Rev. A 102 032619
Google Scholar
[38] Cai W, Han J, Mei F, Yuan X Z, Sun L Y 2019 Phys. Rev. Lett. 123 080501
Google Scholar
-
图 1 一维超导微波腔晶格系统模型图 (a) 该系统由
$ a_n $ 和$ b_n $ 两种超导微波腔组成, 其中$ a_n $ 和$ b_n $ 的耦合系数为$ J_1 $ ,$ b_n $ 和$ a_{n+1} $ 的耦合系数为$ J_2 $ ,$ a_n $ 和$ a_{n+1} $ 的耦合系数为$ T_1 $ ,$ b_n $ 和$ b_{n+1} $ 的耦合系数为$ T_2 $ ; (b) 晶格等价的电路图, 其中$ L_n $ 和$ C_n $ 是超导微波腔总的电感和电容, 他们之间的耦合通过磁通超导量子比特调节Fig. 1. One-dimensional superconducting microwave cavity lattice system model diagram: (a) The system consists of two superconducting microwave cavities
$ a_n $ and$ b_n $ , where$ a_n $ and$ b_n $ coupling coefficient is$ J_1 $ ,$ b_n $ and$ a_{n+1} $ coupling coefficient is$ J_2 $ ,$ a_n $ and$ a_{n+1} $ coupling coefficient is$ T_1 $ ,$ b_n $ and$ b_{n+1} $ coupling coefficient is$ T_2 $ ; (b) equivalent circuit diagram, where$ L_n $ and$ C_n $ are the total inductance and capacitance of the superconducting microwave cavity, and the coupling coefficients can be regulated by the magnetic flux superconducting qubit
图 2 绘制系统能谱E与参数ϕ的物理图像 (a) N = 17时能谱图; (b) N = 18时能谱图, 参数ϕ取值范围为(0,
$ 2\pi $ )Fig. 2. The energy spectrum E of the system via the parameter ϕ: (a) N = 17; (b) N = 18. The range of parameter ϕ is (0,
$ 2\pi $ )
图 3 绘制系统能谱E与奇偶晶格数的物理图像: (a)—(d) N = 17, ϕ分别选取0,
$ \pi/3 $ ,$ 2\pi/3 $ 和π; (e)—(h) N = 18, ϕ分别选取0,$ \pi/4 $ ,$ \pi/2 $ 和πFig. 3. The energy spectrum E of the system via the odd and even lattice numbers: (a)–(d) N = 17,
$ \phi=0 $ ,$ \pi/3 $ ,$ 2\pi/3 $ and π; (e)–(h) N = 18,$ \phi=0 $ ,$ \pi/4 $ ,$ \pi/2 $ and π
图 4 绘制系统零模能级态的分布与奇偶晶格数的物理图像: (a)—(d) N = 17, ϕ分别选取0,
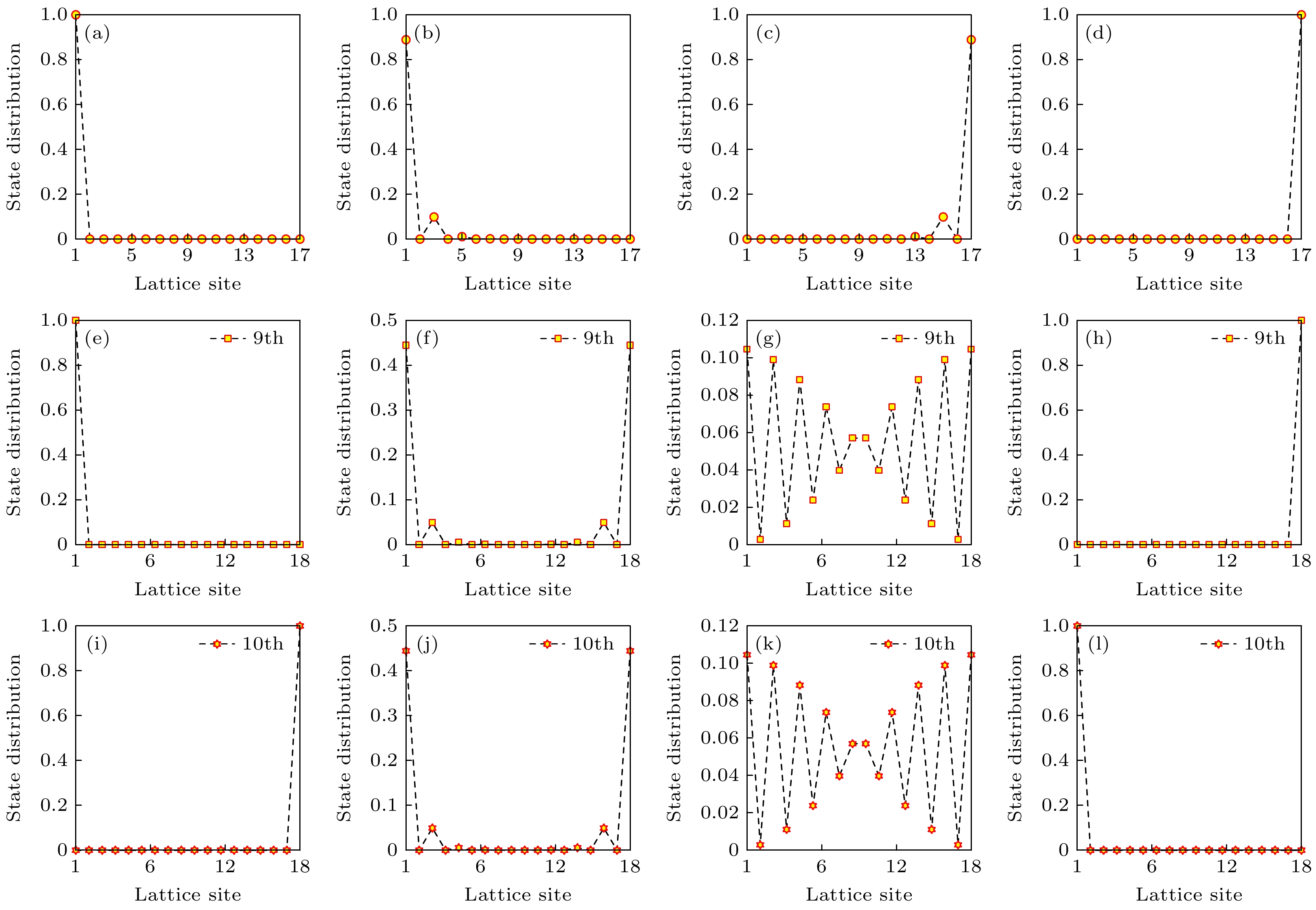
$ \pi/3 $ ,$ 2\pi/3 $ 和π; (e)—(h) N = 18, ϕ分别选取0,$ \pi/3 $ ,$ \pi/2 $ 和$ 1.99\pi $ ; (i)—(l) N = 18, ϕ分别选取0,$ \pi/3 $ ,$ \pi/2 $ 和$ 1.99\pi $ Fig. 4. The state distribution of the zero-mode energy and the odd-even lattice number: (a)–(d) N = 17,
$ \phi=0 $ ,$ \pi/3 $ ,$ 2\pi/3 $ and π; (e)–(h) N = 18,$ \phi=0 $ ,$ \pi/3 $ ,$ \pi/2 $ and$ 1.99\pi $ . (i)–(l) N = 18,$ \phi=0 $ ,$ \pi/3 $ ,$ \pi/2 $ and$ 1.99\pi $ 
图 5 绘制系统能谱E与参数ϕ的物理图像, 选取晶格数N = 17 (a)
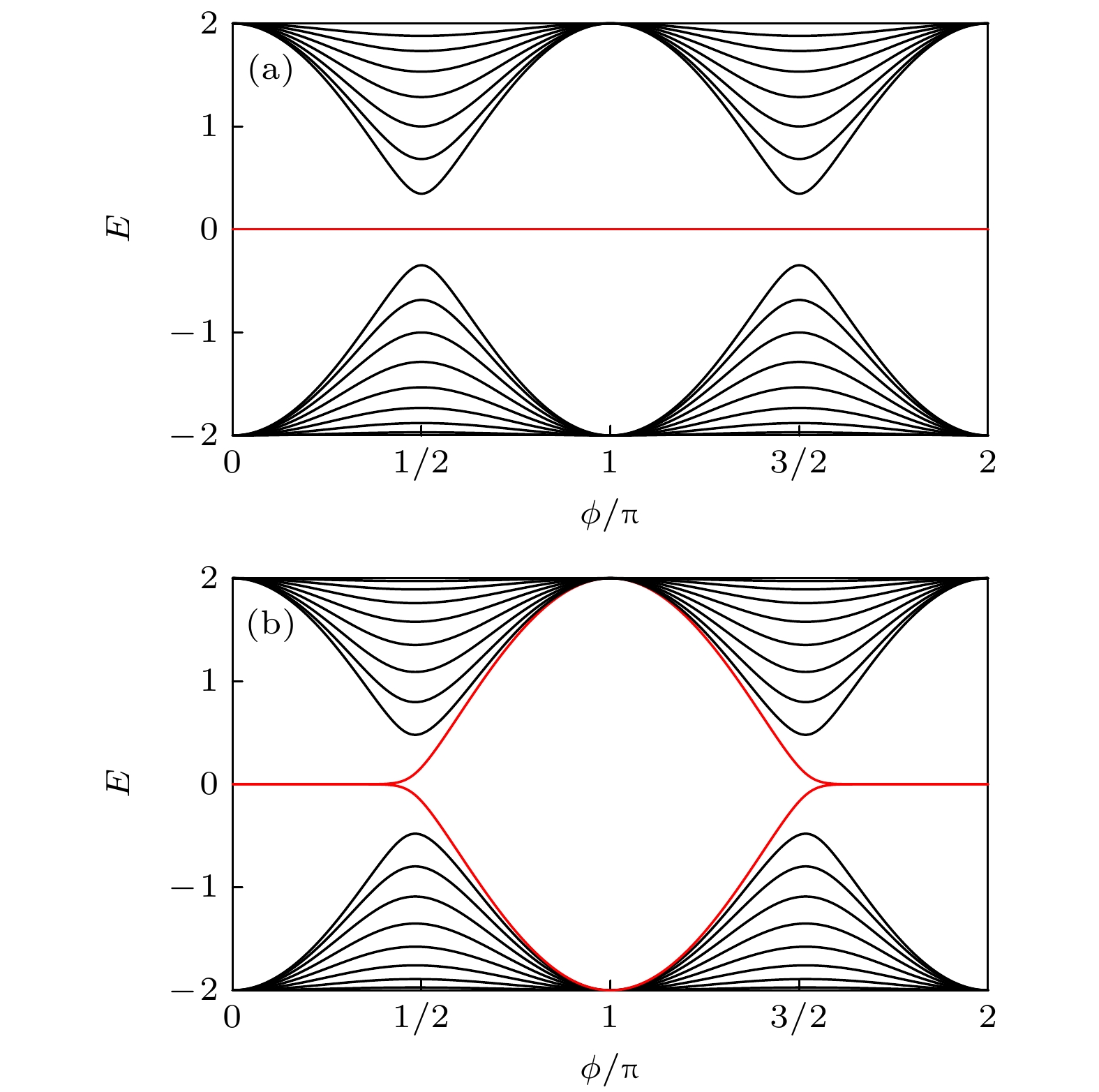
$ T_{1}=0.4 $ ,$ T_{2}=0 $ ; (b)$ T_{1}=0 $ ,$ T_{2}=0.4 $ ; (c)$ T_{1}=0.4 $ ,$ T_{2}=0.3 $ Fig. 5. The energy spectrum E of the system via the parameter ϕ, N = 17: (a)
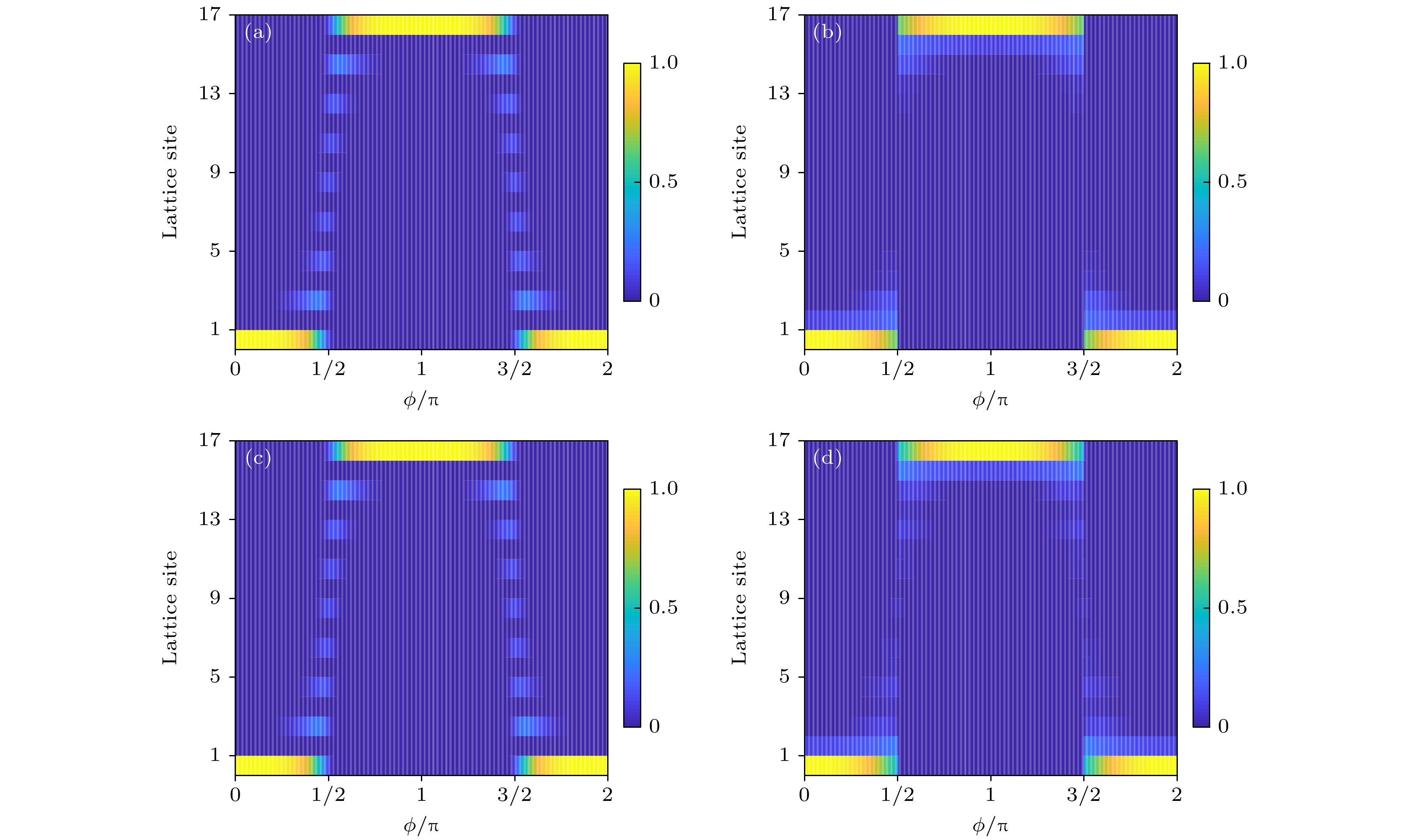
$ T_{1}=0.4 $ ,$ T_{2}=0 $ ; (b)$ T_{1}=0 $ ,$ T_{2}=0.4 $ ; (c)$ T_{1}=0.4 $ ,$ T_{2}=0.3 $ 
图 6 绘制系统能谱E与参数ϕ的物理图像, 选取晶格数N = 18 (a) T1 = 0.2, T2 = 0; (b) T1 = 0, T2 = 0.2; (c) T1 = 0.2, T2 = 0.2
Fig. 6. The energy spectrum E of the system via the parameter ϕ, N = 18: (a)
$ T_{1}=0.2 $ ,$ T_{2}=0 $ ; (b)$ T_{1}=0 $ ,$ T_{2}=0.2 $ ; (c)$ T_{1}=0.2 $ ,$ T_{2}=0.2 $ 
图 7 绘制态的分布与参数ϕ和晶格数的物理图像, 选取晶格数N = 17 (a)
$ T_{1}=0 $ ,$ T_{2}=0 $ ; (b)$ T_{1}=0.6 $ ,$ T_{2}=0 $ ; (c)$ T_{1}= $ $ 0 $ ,$ T_{2}=0.3 $ ; (d)$ T_{1}=0.6 $ ,$ T_{2}=0.3 $ Fig. 7. The state distribution via the lattice numbers and the parameter ϕ, N = 17: (a)
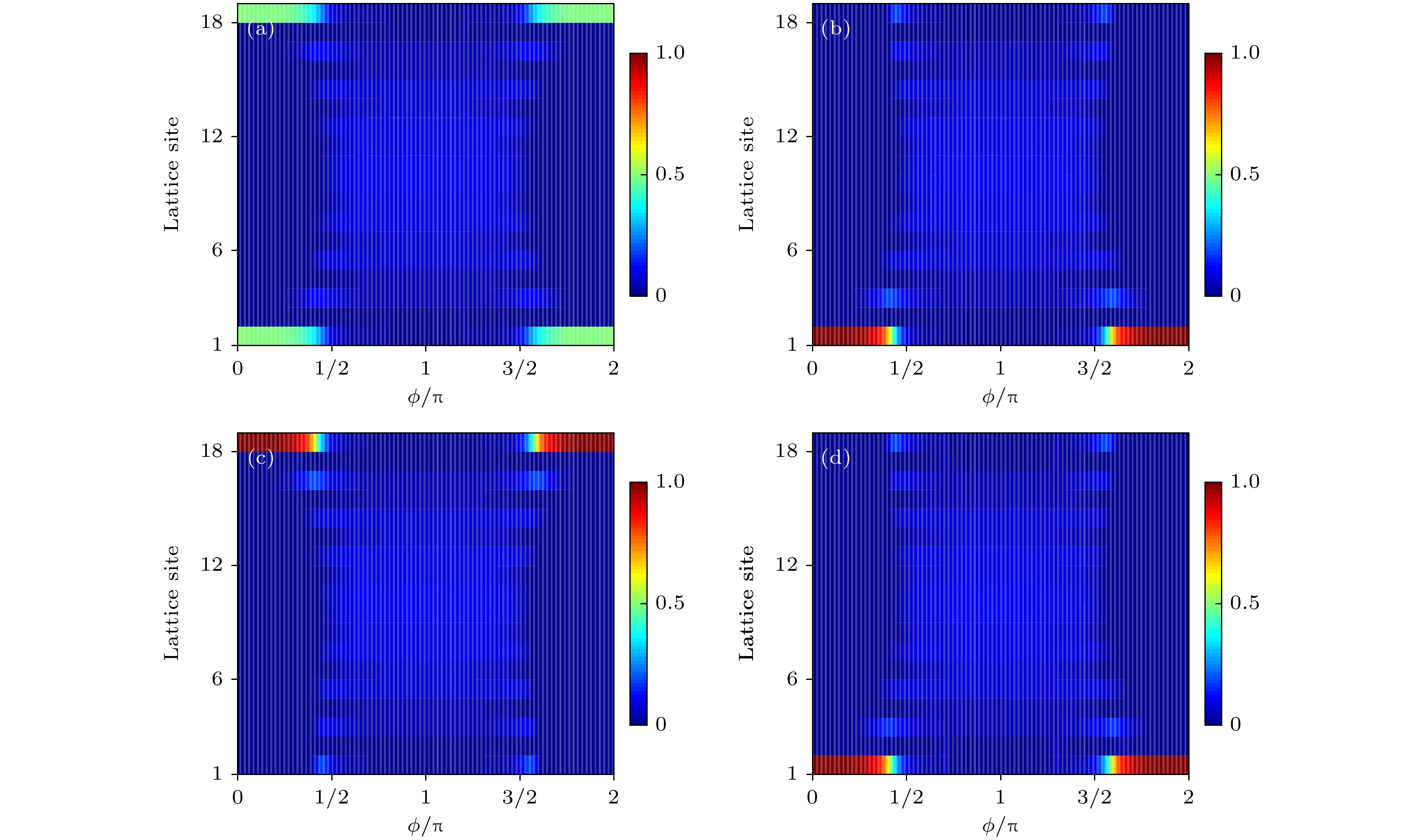
$ T_{1}=0 $ ,$ T_{2}=0 $ ; (b)$ T_{1}=0.6 $ ,$ T_{2}=0 $ ; (c)$ T_{1}=0 $ ,$ T_{2}=0.3 $ ; (d)$ T_{1}=0.6 $ ,$ T_{2}=0.3 $ 
图 8 绘制态的分布与参数ϕ和晶格数的物理图像, 选取晶格数N = 18 (a)
$ T_{1}=0.1 $ ,$ T_{2}=0.1 $ ; (b)$ T_{1}=0.01 $ ,$ T_{2}=0 $ ; (c)$ T_{1}= $ $ 0 $ ,$ T_{2}=0.01 $ ; (d)$ T_{1}=0.2 $ ,$ T_{2}=0.19 $ Fig. 8. The state distribution via the lattice numbers and the parameter ϕ, N = 18: (a)
$ T_{1}=0.1 $ ,$ T_{2}=0.1 $ ; (b)$ T_{1}= 0.01 $ ,$ T_{2}=0 $ ; (c)$ T_{1}=0 $ ,$ T_{2}=0.01 $ ; (d)$ T_{1}=0.2 $ ,$ T_{2}=0.19 $ 
图 9 绘制能谱E与参数ϕ的物理图像, 选取晶格数N = 18 (a) 在第9个和第10个晶格分别加入缺陷势能
$ \text {δ}W=-0.1 $ ,$ \text {δ} W =0.1 $ ; (b) 在第9个和第10个晶格分别加入缺陷势能$ \text {δ} W =0.1 $ ,$ \text {δ} W =-0.1 $ ; (c) 每个晶格引入缺陷势能$ \text {δ} W=0.5 $ ; (d) 每个晶格引入随机位缺陷势能δW = –0.1—0.1; (e) 每个晶格引入随机位缺陷势能δW = –0.3—0.3; (f) 每个晶格引入随机位缺陷势能δW = –0.8—0.8Fig. 9. The energy spectrum E of the system via the parameter ϕ, N = 18: (a) Add defect potentials
$ \text {δ} W=-0.1 $ and$ \text {δ} W=0.1 $ to the 9 and 10 lattices, respectively; (b) add defect potentials$ \text {δ} W=0.1 $ and$ \text {δ}W=-0.1 $ to the 9 and 10 lattices, respectively; (c) each lattice point introduces a defect potential energy$ \text {δ} W=0.5 $ ; (d) potential energy δW = –0.1–0.1 for the introduction of random site defects at lattice point; (e) potential energy δW = –0.3–0.3 for the introduction of random site defects at lattice point; (f) potential energy δW = –0.8–0.8 for the introduction of random site defects at lattice point -
[1] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
Google Scholar
[2] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[3] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004
Google Scholar
[4] Chiu C K, Teo J C Y, Schnyder A P, Ryu S 2016 Rev. Mod. Phys 88 035005
Google Scholar
[5] Xu Z, Zhang Y, Chen S 2017 Phys. Rev. A 96 013606
Google Scholar
[6] Li L, Xu Z, Chen S 2014 Phys. Rev. B 89 085111
Google Scholar
[7] Li L, Chen S 2015 Phys. Rev. B 92 085118
Google Scholar
[8] Mei F, Zhu S L, Zhang Z M, Oh C H, Goldman N 2012 Phys. Rev. A 85 013638
Google Scholar
[9] Xu Z, Zhang R, Chen S, Fu L, Zhang Y 2020 Phys. Rev. A 101 013635
Google Scholar
[10] Wray L A, Xu v, Xia Y, Hsieh D, Fedorov A V, SanHor Y, Cava R J, Bansil A, Lin H, Hasan M Z 2011 Nat. Phys. 7 32
Google Scholar
[11] Malki M, Uhrig G S 2017 Phys. Rev. B 95 235118
Google Scholar
[12] Berg E, Dalla Torre E G, Giamarchi T, Altman E 2008 Phys. Rev. B 77 245119
Google Scholar
[13] Chitov G Y 2018 Phys. Rev. B 97 085131
Google Scholar
[14] Agrapidis C E, van den Brink J, Nishimoto S 2019 Phys. Rev. B 99 224418
Google Scholar
[15] Feng X Y, Zhang G M, Xiang T 2007 Phys. Rev. Lett. 98 087204
Google Scholar
[16] You J Q, Nori F 2011 Nature 474 589
Google Scholar
[17] Devoret M H, Schoelkopf R J 2013 Science 339 1169
Google Scholar
[18] Massel F, Heikkil T T, Pirkkalainen J M, Cho S U, Saloniemi H, Hakonen P J, Sillanpää M A 2011 Nature 480 351
Google Scholar
[19] Teufel J D, Li D, Allman M S, Cicak K, Sirois A J, Whittaker J D, Simmonds R W 2011 Nature 471 204
Google Scholar
[20] Irish E K, Schwab K 2003 Phys. Rev. B 68 155311
Google Scholar
[21] LaHaye M D, Suh J, Echternach P M, Schwab K C, Roukes M L 2009 Nature 459 960
Google Scholar
[22] Wang H F, Zhu A D, Zhang S, Yeon K H 2011 New J. Phys. 13 013021
Google Scholar
[23] Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623
Google Scholar
[24] Blais A, Gambetta J, Wallraff A, Schuster D I, Girvin S M, Devoret M H, Schoelkopf R J 2007 Phys. Rev. A 75 032329
Google Scholar
[25] Ji A C, Sun Q, Xie X C, Liu W M 2009 Phys. Rev. Lett. 102 023602
Google Scholar
[26] Ji A C, Xie X C, Liu W M 2007 Phys. Rev. Lett. 99 183602
Google Scholar
[27] Mei F, Chen G, Tian L, Zhu S L, Jia S 2018 Phys. Rev. A 98 012331
Google Scholar
[28] Mei F, Chen G, Tian L, Zhu S L, Jia S 2018 Phys. Rev. A 98 032323
Google Scholar
[29] Mei F, Xue Z Y, Zhang D W, Tian L, Lee C, Zhu S L 2016 Quantum Sci. Technol. 1 015006
Google Scholar
[30] Zhang Z C, Shao L, Lu W J, Su Y G, Wang Y P, Liu J and Wang X G 2021 Phys. Rev. A 104 053517
Google Scholar
[31] Wang Y P, Zhang Z C, Yu Y F and Zhang Z M 2019 Results Phys. 15 102560
Google Scholar
[32] Koch J, Houck A A, Le Hur K, Girvin S M 2010 Phys. Rev. A 82 043811
Google Scholar
[33] Mei F, You J B, Nie W, Fazio R, Zhu S L, Kwek L C 2015 Phys. Rev. A 92 041805
Google Scholar
[34] Gu F L, Liu J, Mei F, Jia S, Zhang D W, Xue Z Y 2019 npj Quantum Inf. 5 36
[35] Huang Y, Yin Z, Yang W L 2016 Phys. Rev. A 94 022302
Google Scholar
[36] Tan X, Zhao Y, Liu Q, Xue G, Yu H, Wang Z D, Yu Y 2017 npj Quantum Mater. 2 60
Google Scholar
[37] Cao J, Yi X X, Wang H F 2020 Phys. Rev. A 102 032619
Google Scholar
[38] Cai W, Han J, Mei F, Yuan X Z, Sun L Y 2019 Phys. Rev. Lett. 123 080501
Google Scholar
下载:
计量
- 文章访问数: 4043
- PDF下载量: 88
- 被引次数: 0
