Phase field crystal simulation of the effect of temperature on low-angle symmetric tilt grain boundary dislocation motion

Qi Ke-Wu; Zhao Yu-Hong; Guo Hui-Jun; Tian Xiao-Lin; Hou Hua

doi:10.7498/aps.68.20190051

Abstract

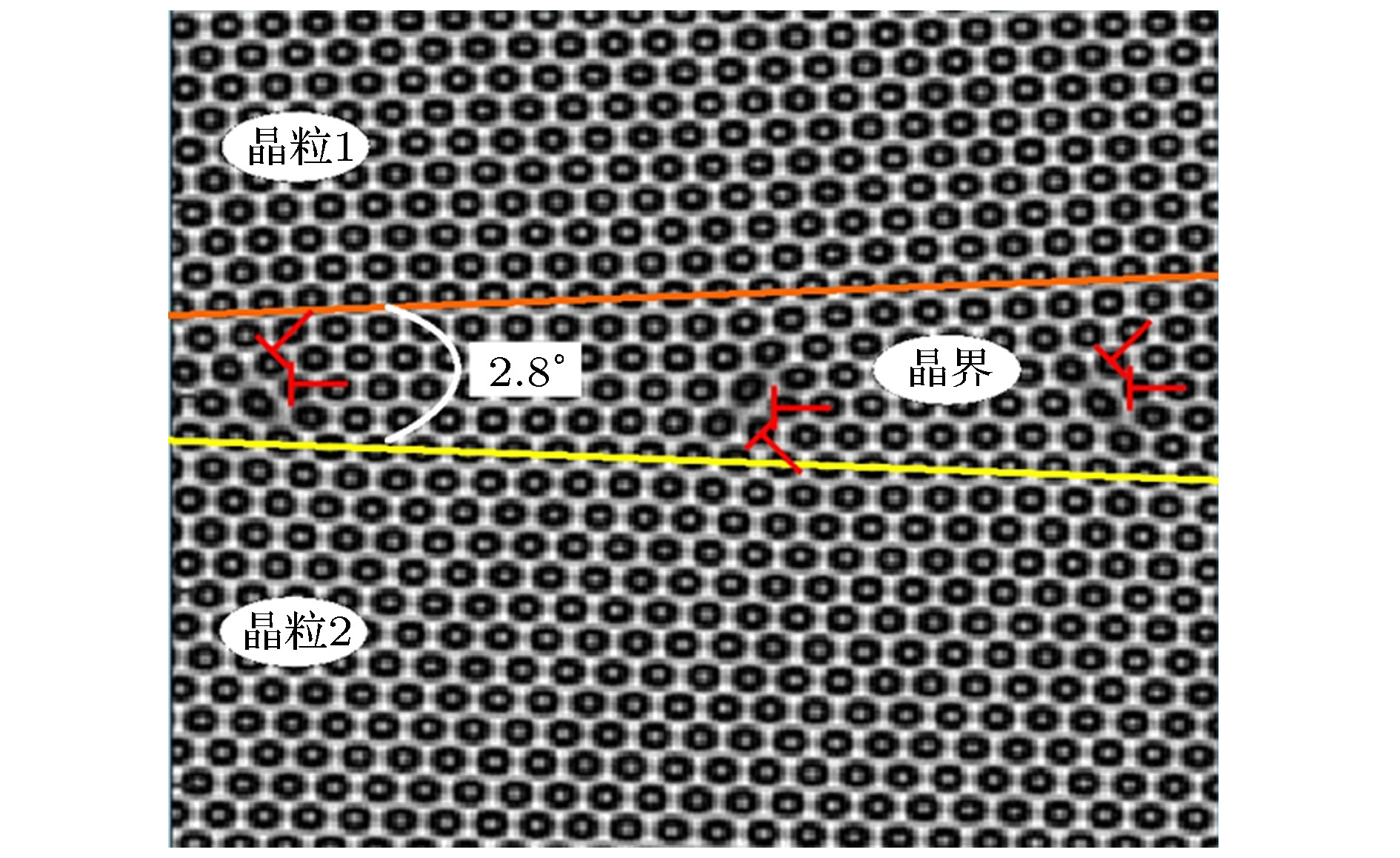
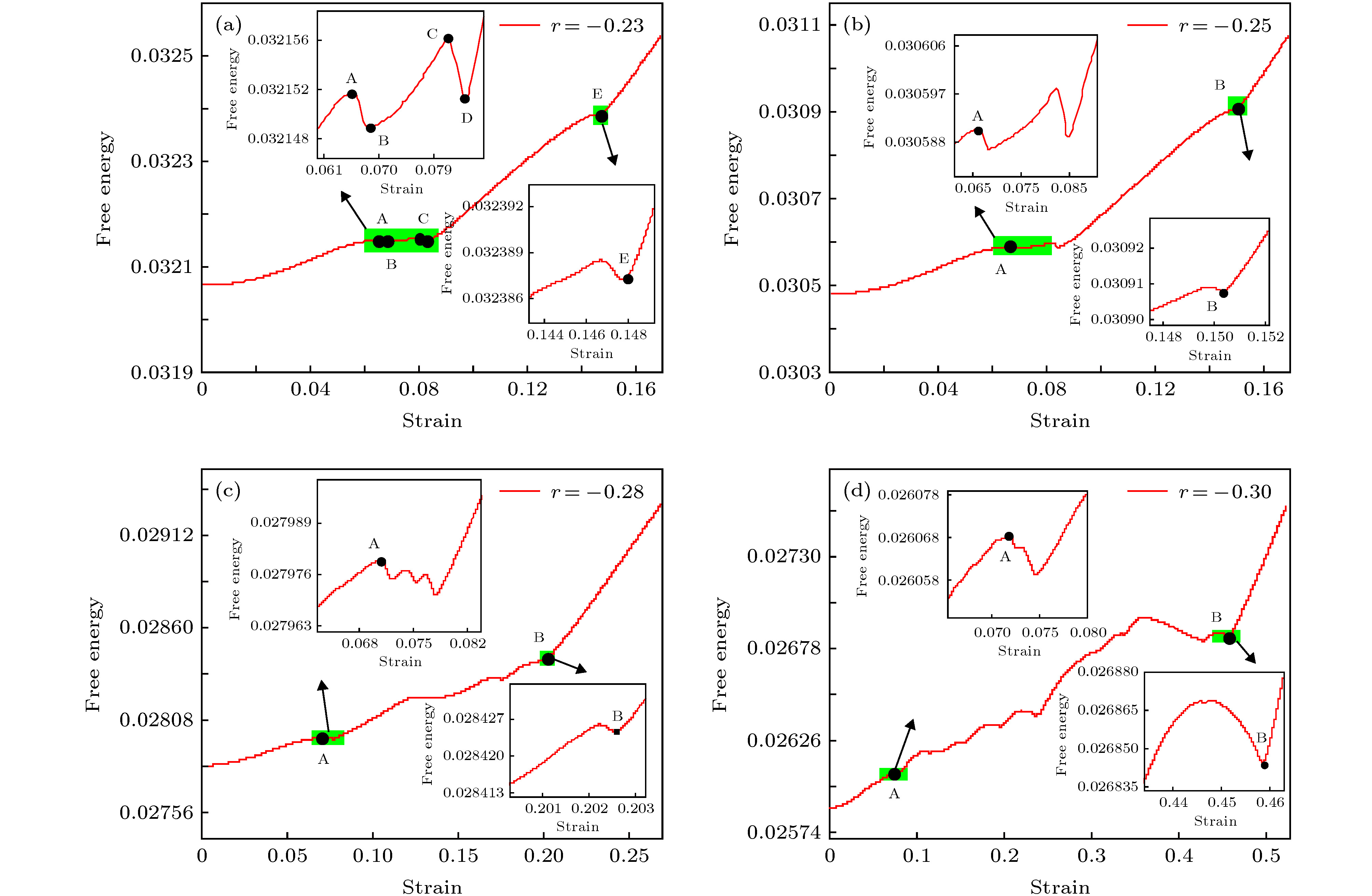
For crystal materials, the grain boundary structure is complex, which is usually the place in which stress concentration and impurity accumulate. Grain boundary structure and movement have a great influence on the macroscopic properties of crystal materials, therefore, it is of great significance to study the microstructure of grain boundary. With the phase filed crystal approach, the structure of low-angle symmetric tilt grain boundary and dislocation motion at nanoscale are studied. The low-angle symmetric tilt grain boundary structure can be described by a dislocation model, in which the grain boundary can be regarded as consisting of a series of edge dislocations at a certain distance. For a relaxation process and applied stress process, the position change of dislocation motion at grain boundaries and the change of free energy density of the system are observed. Furthermore, we also analyze the influence of temperature on the grain boundary structure and the dislocation motion. In the relaxation process, the free energy of the crystal system is higher under high temperature conditions. The results show that the motion of dislocation pairs in the grains can consume the internal energy and release the distortion energy stored at the grain boundary, and thus making the system more stable and the energy reach the lowest value earlier. Simulation results show that the lower the temperature of the system, the faster the free energy density decreases, the faster the regular arrangement rate of atoms increases, the shorter the time required for the free energy density to reach a stable state becomes. And when the grain boundary reaches a steady state, the arrangement of the dislocations becomes more and more regular and arranges in a straight line. For an applied stress process, with the decrease of temperature, the time required for the first encounter of dislocation pairs and the time required for the formation of single crystal become longer, and it takes more time for the first encounter of dislocation pairs in crystals to disappear completely. Further studies also show that with the decrease of temperature, the free energy density exhibits a multi-stage ascending and descending process. The rising process of energy curve corresponds to the stage of dislocation climbing along the grain boundary, and the decline process corresponds to the stage of dislocation decomposition and encounter annihilation. At the same time, the dislocation pairs’ reaction becomes more complex. Finally, the dislocations annihilate with each other.

Keywords:

Authors and contacts

Material Science and Engineering Institute, North University of China, Taiyuan 030051, China

Corresponding author: Zhao Yu-Hong, zhaoyuhong@nuc.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51774254, 51774253, 51701187, U1610123, 51674226, 51574207, 51574206) and the Science and Technology Major Project of Shanxi Province, China (Grant No. MC2016-06).

FullText HTML : translate this paragraph

References

[1]	Paul S K 2018 Comput. Mater. Sci. 150 24 Google Scholar
[2]	Bobylev S V, Gutkin M Y, Ovid'Ko I A 2006 Phys. Solid State 48 1495 Google Scholar
[3]	Caturla M, Nieh T G, Stolken J S 2004 Appl. Phys. Lett. 84 598 Google Scholar
[4]	Peter S, Mikko H, Nikolas P 2009 Phys. Rev. E 80 046107 Google Scholar
[5]	Li X H, Wen X, Zhao H H, Ma Z Q, Yu L M, Li C, Liu C X, Guo Q Y, Liu Y C 2019 J. Alloys Compd. 779 175 Google Scholar
[6]	Chen Y Y, Hu Z P, Xu Y F, Wang J Y, Schützendübe P, Huang Y, Liu Y C, Wang Z M 2019 J. Mater. Sci. Technol. 35 512 Google Scholar
[7]	Elder K R, Katakowski M, Haataja M, Grant M 2002 Phys. Rev. Lett. 88 245701 Google Scholar
[8]	Elder K R, Grant M 2004 Phys. Rev. E 70 051605 Google Scholar
[9]	Elder K R, Provatas N, Berry J, Stefanovic P 2007 Phys. Rev. B 75 064107 Google Scholar
[10]	Wang J, Yu L M, Huang Y, Li H J , Liu Y C 2019 Comput. Mater. Sci. 160 105 Google Scholar
[11]	Qi Y, Krajewski P E 2007 Acta Mater. 55 1555 Google Scholar
[12]	郑晓娟, 赵宇宏, 侯华, 靳玉春, 马庆爽, 田晋忠 2017 中国有色金属学报 27 2098 Zheng X J, Zhao Y H, Hou H, Jin Y C, Ma Q S, Tian J Z 2017 Chin. J. Nonferrous Met. 27 2098
[13]	Fan D, Chen L Q 1997 Acta Mater. 45 611 Google Scholar
[14]	孙远洋, 赵宇宏, 侯华, 郑晓娟, 郭慧俊 2018 稀有金属材料与工程 47 3000 Sun Y Y, Zhao Y H, Hou H, Zheng X J, Guo H J 2018 Rare Metal. Mater. Eng. 47 3000
[15]	康永生, 赵宇宏, 侯华, 靳玉春, 陈利文 2016 65 188102 Google Scholar Kang Y S, Zhao Y H, Hou H, Jin Y C, Chen L W 2016 Acta Phys. Sin. 65 188102 Google Scholar
[16]	王锟, 赵宇宏, 杨东然, 侯华, 王欣然, 田园 2015 稀有金属材料与工程 44 939 Wang K, Zhao Y H, Yang D R, Hou H, Wang X R, Tian Y 2015 Rare Metal. Mater. Eng. 44 939
[17]	赵宇宏 2010 材料相变过程微观组织模拟 (北京: 国防工业出版社) 第139页 Zhao Y H 2010 Simulation for the Materials Microstructure Evolution in Phase Transformation Process (Beijing: National Defense Industry Press) p139 (in Chinese)
[18]	孙远洋, 赵宇宏, 侯华, 靳玉春, 郑晓娟 2018 中国有色金属学报 28 71 Sun Y Y, Zhao Y H, Hou H, Jin Y C, Zheng X J 2018 Chin. J. Nonferrous Metal. 28 71
[19]	田晓林, 赵宇宏, 田晋忠, 侯华 2018 67 230201 Google Scholar Tian X L, Zhao Y H, Tian J Z, Hou H 2018 Acta Phys. Sin. 67 230201 Google Scholar
[20]	Zhao Y H, Tian X L, Zhao B J, Sun Y Y, Guo H J, Dong M Y, Liu H, Wang X J, Guo Z H, Umar A, Hou H 2018 Sci. Adv. Mater. 10 1793 Google Scholar
[21]	Fallah V, Stolle J, Ofori-Opoku N, Esmaeili S, Provatas N 2012 Phys. Rev. B 86 3209
[22]	Fallah V, Ofori-Opoku N, Stolle J, Provatas N, Esmaeili S 2013 Acta Mater. 61 3653 Google Scholar
[23]	Wu K A, Voorhees P W 2012 Acta Mater. 60 407 Google Scholar
[24]	Yamanaka A, McReynolds K, Voorhees P W 2017 Acta Mater. 133 160 Google Scholar
[25]	Olmsted D L, Buta D, Adland A, Foiles S M, Asta M, Karma A 2011 Phys. Rev. Lett. 106 046101 Google Scholar
[26]	高英俊, 秦河林, 周文权, 邓芊芊, 罗志荣, 黄创高 2015 64 106105 Google Scholar Gao Y J, Qin H L, Zhou W Q, Deng Q Q, Luo Z R, Huang C G 2015 Acta Phys. Sin. 64 106105 Google Scholar
[27]	Berry J, Elder K R, Grant M 2008 Phys. Rev. B 77 224114 Google Scholar
[28]	Chan V W L, Pisutha-Arnond N, Thornton K 2017 Comput. Mater. Sci. 135 205 Google Scholar
[29]	Asadi E, Zaeem M A 2015 JOM 67 186 Google Scholar
[30]	Tang S, Wang Z J, Guo Y L, Wang J C, Yu Y M, Zhou Y H 2012 Acta Mater. 60 5501 Google Scholar
[31]	Berry J, Grant M 2014 Phys. Rev. E: Stat. Nonlinear Soft Matter Phys. 89 062303 Google Scholar
[32]	Zhang W, Mi J 2016 IOP Conf. Ser.: Mater. Sci. Eng. 117 012056 Google Scholar
[33]	Hu S, Chen Z, Xi W, Peng Y Y 2017 J. Mater. Sci. 52 5641 Google Scholar
[34]	Hu S, Xi W, Chen Z, Wang S, Zhang T H 2017 Comput. Mater. Sci. 132 125 Google Scholar
[35]	Hu S, Chen Z, Peng Y Y, Liu Y J, Guo L Y 2016 Comput. Mater. Sci. 121 143 Google Scholar
[36]	谷季唯, 王锦程, 王志军, 李俊杰, 郭灿, 唐赛 2017 66 216101 Google Scholar Gu J W, Wang J C, Wang Z J, Li J J, Guo C, Tang S 2017 Acta Phys. Sin. 66 216101 Google Scholar
[37]	Hirouchi T, Takaki T, Tomita Y 2010 Int. J. Mech. Sci. 52 309 Google Scholar
[38]	Guo H J, Zhao Y H, Sun Y Y, Tian J Z, Hou H, Qi K W, Tian X L 2019 Superlattices Microstruct. 129 163 Google Scholar
[39]	Zhao Y H, Deng S J, Liu H, Zhang J X, Guo Z H, Hou H 2018 Comput. Mater. Sci. 154 365 Google Scholar
[40]	Wen Z Q, Hou H, Tian J Z, Zhao Y H, Li H J, Han P D 2018 Intermetallics 92 15 Google Scholar
[41]	Wen Z Q, Zhao Y H, Hou H, Wang B, Han P D 2017 Mater. Des. 114 398 Google Scholar
[42]	Zhao Y H, Qi L, Jin Y C, Wang K, Tian J Z, Han P D 2015 J. Alloys Compd. 647 1104 Google Scholar
[43]	Tian J Z, Zhao Y H, Hou H, Han P D 2017 Solid State Commun. 268 44 Google Scholar
[44]	Hirouchi T, Takaki T, Tomita Y 2009 Comput. Mater. Sci. 44 1192 Google Scholar

Cited By

图 1 单模近似下的二维相图(图中阴影部分表示两相区)

Figure 1. Two-dimensional phase diagram as calculated in a one-mode approximation (hatched areas in the figure correspond to coexistence regions).

DownLoad: Full-Size Img PowerPoint

图 2 r = –0.25条件下弛豫过程模拟　(a) n = 300; (b) n = 800; (c) n = 15000; (d) n = 29450

Figure 2. Simulation of relaxation process under the conditions of temperature r = –0.25 at (a) n = 300, (b) n = 800, (c) n = 15000, (d) n = 29450.

DownLoad: Full-Size Img PowerPoint

图 3 两晶粒形成夹角为2.8°的位向角

Figure 3. Snapshot of two grains with an orientation angle of 2.8°.

DownLoad: Full-Size Img PowerPoint

图 4 弛豫过程29500步时不同温度条件下晶界位错模拟图　(a) r = –0.23; (b) r = –0.25; (c) r = –0.28; (d) r = –0.30

Figure 4. Simulation of grain boundary dislocation under different temperature conditions at 29500 steps of relaxation process: (a) r = –0.23; (b) r = –0.25; (c) r = –0.28; (d) r = –0.30

DownLoad: Full-Size Img PowerPoint

图 5 温度对弛豫过程体系自由能变化的影响

Figure 5. Effect of temperature on the change of free energy of relaxation process system.

DownLoad: Full-Size Img PowerPoint

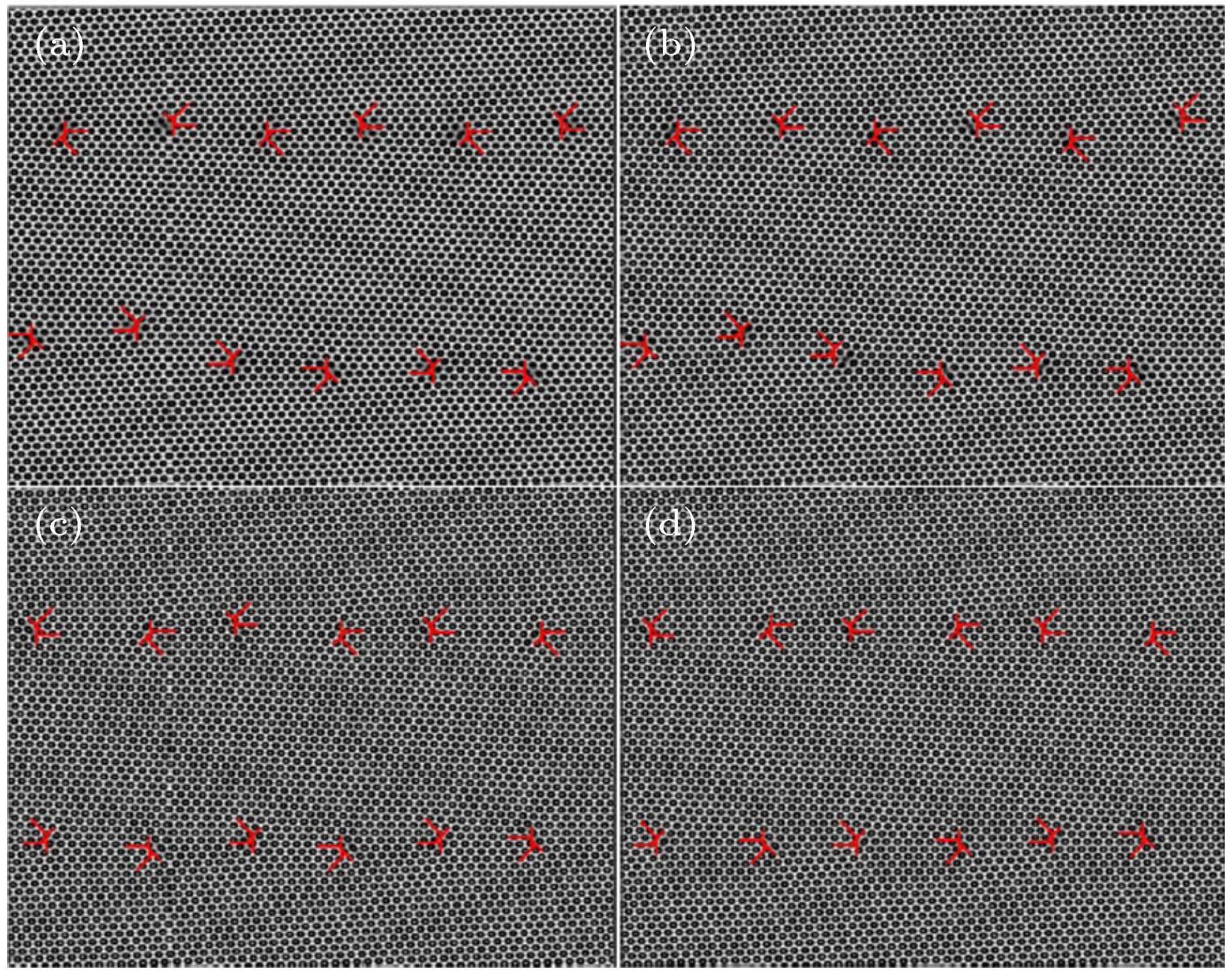
图 6 应力作用下r = –0.23时晶界位错运动模拟图　(a) n = 5500; (b) n = 10900; (c) n = 11350; (d) n = 13350; (e) n = 13850; (f) n = 24450

Figure 6. Simulation diagram of grain boundary dislocation motion under stress with r = –0.23: (a) n = 5500; (b) n = 10900; (c) n = 11350; (d) n = 13350; (e) n = 13850; (f) n = 24450.

DownLoad: Full-Size Img PowerPoint

图 7 应力作用下r = –0.25时晶界位错运动模拟图　(a) n = 11100; (b) n = 11550; (c) n = 13600; (d) n = 13850; (e) n = 14100; (f) n = 25150

Figure 7. Simulation diagram of grain boundary dislocation motion under stress with r = –0.25: (a) n = 11100; (b) n = 11550; (c) n = 13600; (d) n = 13850; (e) n = 14100; (f) n = 25150.

DownLoad: Full-Size Img PowerPoint

图 9 应力作用下r = –0.30时晶界位错运动模拟图　(a) n = 11300; (b) n = 12100; (c) n = 12500; (d) n = 39550; (e) n = 40100; (f) n = 76500

Figure 9. Simulation diagram of grain boundary dislocation motion under stress with r = –0.30: (a) n = 11300; (b) n = 12100; (c) n = 12500; (d) n = 39550; (e) n = 40100; (f) n = 76500.

DownLoad: Full-Size Img PowerPoint

图 8 应力作用下r = –0.28时晶界位错运动模拟图　(a) n = 11800; (b) n = 12050; (c) n = 13800; (d) n = 29050; (e) n = 33450; (f) n = 33700

Figure 8. Simulation diagram of grain boundary dislocation motion under stress with r = –0.28: (a) n = 11800; (b) n = 12050; (c) n = 13800; (d) n = 29050; (e) n = 33450; (f) n = 33700.

DownLoad: Full-Size Img PowerPoint

图 10 11200步时不同温度条件下的模拟图　(a) r = –0.23; (b) r = –0.25; (c) r = –0.28; (d) r = –0.30

Figure 10. Simulation diagram under different temperature conditions at n = 11200: (a) r = –0.23; (b) r = –0.25; (c) r = –0.28; (d) r = –0.30.

DownLoad: Full-Size Img PowerPoint

图 11 不同温度下体系自由能曲线图　(a) r = –0.23; (b) r = –0.25; (c) r = –0.28; (d) r = –0.30

Figure 11. Free energy curve of system under different degrees of temperature: (a) r = –0.23; (b) r = –0.25; (c) r = –0.28; (d) r = –0.30

DownLoad: Full-Size Img PowerPoint

表 1 模拟所采用的参数

Table 1. Parameters used in the simulation.

方案初始原子密度ρ₀ 位向差θ 温度相关参量r

A 0.285 2.8° –0.23
B 0.285 2.8° –0.25
C 0.285 2.8° –0.28
D 0.285 2.8° –0.30

DownLoad: CSV

map

[1]	Paul S K 2018 Comput. Mater. Sci. 150 24 Google Scholar
[2]	Bobylev S V, Gutkin M Y, Ovid'Ko I A 2006 Phys. Solid State 48 1495 Google Scholar
[3]	Caturla M, Nieh T G, Stolken J S 2004 Appl. Phys. Lett. 84 598 Google Scholar
[4]	Peter S, Mikko H, Nikolas P 2009 Phys. Rev. E 80 046107 Google Scholar
[5]	Li X H, Wen X, Zhao H H, Ma Z Q, Yu L M, Li C, Liu C X, Guo Q Y, Liu Y C 2019 J. Alloys Compd. 779 175 Google Scholar
[6]	Chen Y Y, Hu Z P, Xu Y F, Wang J Y, Schützendübe P, Huang Y, Liu Y C, Wang Z M 2019 J. Mater. Sci. Technol. 35 512 Google Scholar
[7]	Elder K R, Katakowski M, Haataja M, Grant M 2002 Phys. Rev. Lett. 88 245701 Google Scholar
[8]	Elder K R, Grant M 2004 Phys. Rev. E 70 051605 Google Scholar
[9]	Elder K R, Provatas N, Berry J, Stefanovic P 2007 Phys. Rev. B 75 064107 Google Scholar
[10]	Wang J, Yu L M, Huang Y, Li H J , Liu Y C 2019 Comput. Mater. Sci. 160 105 Google Scholar
[11]	Qi Y, Krajewski P E 2007 Acta Mater. 55 1555 Google Scholar
[12]	郑晓娟, 赵宇宏, 侯华, 靳玉春, 马庆爽, 田晋忠 2017 中国有色金属学报 27 2098 Zheng X J, Zhao Y H, Hou H, Jin Y C, Ma Q S, Tian J Z 2017 Chin. J. Nonferrous Met. 27 2098
[13]	Fan D, Chen L Q 1997 Acta Mater. 45 611 Google Scholar
[14]	孙远洋, 赵宇宏, 侯华, 郑晓娟, 郭慧俊 2018 稀有金属材料与工程 47 3000 Sun Y Y, Zhao Y H, Hou H, Zheng X J, Guo H J 2018 Rare Metal. Mater. Eng. 47 3000
[15]	康永生, 赵宇宏, 侯华, 靳玉春, 陈利文 2016 65 188102 Google Scholar Kang Y S, Zhao Y H, Hou H, Jin Y C, Chen L W 2016 Acta Phys. Sin. 65 188102 Google Scholar
[16]	王锟, 赵宇宏, 杨东然, 侯华, 王欣然, 田园 2015 稀有金属材料与工程 44 939 Wang K, Zhao Y H, Yang D R, Hou H, Wang X R, Tian Y 2015 Rare Metal. Mater. Eng. 44 939
[17]	赵宇宏 2010 材料相变过程微观组织模拟 (北京: 国防工业出版社) 第139页 Zhao Y H 2010 Simulation for the Materials Microstructure Evolution in Phase Transformation Process (Beijing: National Defense Industry Press) p139 (in Chinese)
[18]	孙远洋, 赵宇宏, 侯华, 靳玉春, 郑晓娟 2018 中国有色金属学报 28 71 Sun Y Y, Zhao Y H, Hou H, Jin Y C, Zheng X J 2018 Chin. J. Nonferrous Metal. 28 71
[19]	田晓林, 赵宇宏, 田晋忠, 侯华 2018 67 230201 Google Scholar Tian X L, Zhao Y H, Tian J Z, Hou H 2018 Acta Phys. Sin. 67 230201 Google Scholar
[20]	Zhao Y H, Tian X L, Zhao B J, Sun Y Y, Guo H J, Dong M Y, Liu H, Wang X J, Guo Z H, Umar A, Hou H 2018 Sci. Adv. Mater. 10 1793 Google Scholar
[21]	Fallah V, Stolle J, Ofori-Opoku N, Esmaeili S, Provatas N 2012 Phys. Rev. B 86 3209
[22]	Fallah V, Ofori-Opoku N, Stolle J, Provatas N, Esmaeili S 2013 Acta Mater. 61 3653 Google Scholar
[23]	Wu K A, Voorhees P W 2012 Acta Mater. 60 407 Google Scholar
[24]	Yamanaka A, McReynolds K, Voorhees P W 2017 Acta Mater. 133 160 Google Scholar
[25]	Olmsted D L, Buta D, Adland A, Foiles S M, Asta M, Karma A 2011 Phys. Rev. Lett. 106 046101 Google Scholar
[26]	高英俊, 秦河林, 周文权, 邓芊芊, 罗志荣, 黄创高 2015 64 106105 Google Scholar Gao Y J, Qin H L, Zhou W Q, Deng Q Q, Luo Z R, Huang C G 2015 Acta Phys. Sin. 64 106105 Google Scholar
[27]	Berry J, Elder K R, Grant M 2008 Phys. Rev. B 77 224114 Google Scholar
[28]	Chan V W L, Pisutha-Arnond N, Thornton K 2017 Comput. Mater. Sci. 135 205 Google Scholar
[29]	Asadi E, Zaeem M A 2015 JOM 67 186 Google Scholar
[30]	Tang S, Wang Z J, Guo Y L, Wang J C, Yu Y M, Zhou Y H 2012 Acta Mater. 60 5501 Google Scholar
[31]	Berry J, Grant M 2014 Phys. Rev. E: Stat. Nonlinear Soft Matter Phys. 89 062303 Google Scholar
[32]	Zhang W, Mi J 2016 IOP Conf. Ser.: Mater. Sci. Eng. 117 012056 Google Scholar
[33]	Hu S, Chen Z, Xi W, Peng Y Y 2017 J. Mater. Sci. 52 5641 Google Scholar
[34]	Hu S, Xi W, Chen Z, Wang S, Zhang T H 2017 Comput. Mater. Sci. 132 125 Google Scholar
[35]	Hu S, Chen Z, Peng Y Y, Liu Y J, Guo L Y 2016 Comput. Mater. Sci. 121 143 Google Scholar
[36]	谷季唯, 王锦程, 王志军, 李俊杰, 郭灿, 唐赛 2017 66 216101 Google Scholar Gu J W, Wang J C, Wang Z J, Li J J, Guo C, Tang S 2017 Acta Phys. Sin. 66 216101 Google Scholar
[37]	Hirouchi T, Takaki T, Tomita Y 2010 Int. J. Mech. Sci. 52 309 Google Scholar
[38]	Guo H J, Zhao Y H, Sun Y Y, Tian J Z, Hou H, Qi K W, Tian X L 2019 Superlattices Microstruct. 129 163 Google Scholar
[39]	Zhao Y H, Deng S J, Liu H, Zhang J X, Guo Z H, Hou H 2018 Comput. Mater. Sci. 154 365 Google Scholar
[40]	Wen Z Q, Hou H, Tian J Z, Zhao Y H, Li H J, Han P D 2018 Intermetallics 92 15 Google Scholar
[41]	Wen Z Q, Zhao Y H, Hou H, Wang B, Han P D 2017 Mater. Des. 114 398 Google Scholar
[42]	Zhao Y H, Qi L, Jin Y C, Wang K, Tian J Z, Han P D 2015 J. Alloys Compd. 647 1104 Google Scholar
[43]	Tian J Z, Zhao Y H, Hou H, Han P D 2017 Solid State Commun. 268 44 Google Scholar
[44]	Hirouchi T, Takaki T, Tomita Y 2009 Comput. Mater. Sci. 44 1192 Google Scholar

[1]	Gao Feng, Li Huan-Qing, Song Zhuo, Zhao Yu-Hong. The Evolution of Grain Boundary Dislocations in Graphene Induced by Strain: Three-Mode Phase-Field Crystal Method. Acta Physica Sinica, 2024, 73(24): . doi: 10.7498/aps.73.20241368
[2]	Chen Wei-Long, Guo Rong-Rong, Tong Yu-Shen, Liu Li-Li, Zhou Sheng-Lan, Lin Jin-Hai. Influence of sub-bandgap illumination on electric field distribution at grain boundary in CdZnTe crystals. Acta Physica Sinica, 2022, 71(22): 226101. doi: 10.7498/aps.71.20220896
[3]	Guo Can, Zhao Yu-Ping, Deng Ying-Yuan, Zhang Zhong-Ming, Xu Chun-Jie. A phase-field study on interaction process of moving grain boundary and spinodal decomposition. Acta Physica Sinica, 2022, 71(7): 078101. doi: 10.7498/aps.71.20211973
[4]	Zhang Bo-Jia, An Min-Rong, Hu Teng, Han La. Molecular dynamics simulation of mechanism of interaction between dislocation and amorphism in magnesium. Acta Physica Sinica, 2022, 71(14): 143101. doi: 10.7498/aps.71.20212318
[5]	Xia Wen-Qiang, Zhao Yan, Liu Zhen-Zhi, Lu Xiao-Gang. Phase field crystal simulation of strain-induced square phase low-angle symmetric tilt grain boundary dislocation reaction. Acta Physica Sinica, 2022, 71(9): 096102. doi: 10.7498/aps.71.20212278
[6]	Li Shuai-Yao, Zhang Da-Yuan, Gao Qiang, Li Bo, He Yong, Wang Zhi-Hua. Temperature measurement in combustion flow field with femtosecond laser-induced filament. Acta Physica Sinica, 2020, 69(23): 234207. doi: 10.7498/aps.69.20200939
[7]	Qi Ke-Wu, Zhao Yu-Hong, Tian Xiao-Lin, Peng Dun-Wei, Sun Yuan-Yang, Hou Hua. Phase field crystal simulation of effect of misorientation angle on low-angle asymmetric tilt grain boundary dislocation motion. Acta Physica Sinica, 2020, 69(14): 140504. doi: 10.7498/aps.69.20200133
[8]	He Ju-Sheng, Zhang Meng, Zou Ji-Jun, Pan Hua-Qing, Qi Wei-Jing, Li Ping. Analyses of determination conditions of n-GaN dislocation density by triple-axis X-ray diffraction. Acta Physica Sinica, 2017, 66(21): 216102. doi: 10.7498/aps.66.216102
[9]	Guo Liu-Yang, Chen Zheng, Long Jian, Yang Tao. Study on the effect of stress state and crystal orientation on micro-crack tip propagation behavior in phase field crystal method. Acta Physica Sinica, 2015, 64(17): 178102. doi: 10.7498/aps.64.178102
[10]	Yang Jian-Qun, Ma Guo-Liang, Li Xing-Ji, Liu Chao-Ming, Liu Hai. Compressive behavior of nanocrystalline nickel at various temperatures and strain rates. Acta Physica Sinica, 2015, 64(13): 137103. doi: 10.7498/aps.64.137103
[11]	Gao Ying-Jun, Qin He-Lin, Zhou Wen-Quan, Deng Qian-Qian, Luo Zhi-Rong, Huang Chuang-Gao. Phase field crystal simulation of grain boundary annihilation under strain strain at high temperature. Acta Physica Sinica, 2015, 64(10): 106105. doi: 10.7498/aps.64.106105
[12]	Shao Yu-Fei, Yang Xin, Li Jiu-Hui, Zhao Xing. Atomistic simulation study on the local strain fields around an extended edge dislocation in copper. Acta Physica Sinica, 2014, 63(7): 076103. doi: 10.7498/aps.63.076103
[13]	Lu Na, Wang Yong-Xin, Chen Zheng. Phase field crystal study on asymmetrical tilt subgrain boundaries. Acta Physica Sinica, 2014, 63(18): 180508. doi: 10.7498/aps.63.180508
[14]	Gao Ying-Jun, Luo Zhi-Rong, Huang Chuang-Gao, Lu Qiang-Hua, Lin Kui. Phase-field-crystal modeling for two-dimensional transformation from hexagonal to square structure. Acta Physica Sinica, 2013, 62(5): 050507. doi: 10.7498/aps.62.050507
[15]	Zhao Yu-Long, Chen Zheng, Long Jian, Yang Tao. Phase field crystal simulation of microscopic deformation mechanism of reverse Hall-Petch effect in nanocrystalline materials. Acta Physica Sinica, 2013, 62(11): 118102. doi: 10.7498/aps.62.118102
[16]	Long Jian, Wang Zhao-Yu, Zhao Yu-Long, Long Qing-Hua, Yang Tao, Chen Zheng. Phase field crystal study on grain boundary evolution and its micro-mechanism under various symmetry. Acta Physica Sinica, 2013, 62(21): 218101. doi: 10.7498/aps.62.218101
[17]	Li Lian-He, Liu Guan-Ting. A screw dislocation interacting with a wedge-shaped crack in one-dimensional hexagonal quasicrystals. Acta Physica Sinica, 2012, 61(8): 086103. doi: 10.7498/aps.61.086103
[18]	Chen Cheng, Chen Zheng, Zhang Jing, Yang Tao. Simulation of morphological evolution and crystallographic tilt in heteroepitaxial growth using phase-field crystal method. Acta Physica Sinica, 2012, 61(10): 108103. doi: 10.7498/aps.61.108103
[19]	Li Yan, Fu Hai-Wei, Shao Min, Li Xiao-Li. Temperature characteristic of photonic crystals resonant cavitycomposed of GaAs pillars with graphite lattice. Acta Physica Sinica, 2011, 60(7): 074219. doi: 10.7498/aps.60.074219
[20]	Fang Bu-Qing, Lu Guo, Zhang Guang-Cai, Xu Ai-Guo, Li Ying-Jun. Evolution of stacking-fault-tetrahedron-like structures in copper crystal. Acta Physica Sinica, 2009, 58(7): 4862-4871. doi: 10.7498/aps.58.4862

Catalog

Vol. 68, Issue 17 - 2019-09-05

Metrics

Abstract views: 10767
PDF Downloads: 99
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板