-
采用晶体相场法研究了外加应变作用下, 不同取向差的四方相对称倾侧小角度晶界的位错运动与反应及反应过程中的位错组态, 通过采用几何相位法对位错周围应变场进行了表征. 结果表明, 凝固弛豫达到稳态后, 晶界两侧位错平行且方向相反, 随晶界两侧晶粒取向差增大, 位错数目增加, 距离减小, 且体系自由能增加. 在外加应变作用下, 晶界位错经历攀移、发射、反应湮灭等阶段, 体系自由能呈现波动. 当取向差增大时, 位错运动方式由攀移向攀滑移转变, 产生更多类型的位错组构型, 并发生相应的位错与位错组之间的反应. 对于不同构型的位错反应, 正切应变驱动位错靠近, 负切应变驱动位错湮灭.In this paper, the phase field crystal method is used to study the dislocation motion and reaction of the square phase symmetric tilt low-angle grain boundaries, and the dislocation configurations with different misorientation angles are analyzed under the action of applied strain. The geometric phase approach is used to characterize the strain field around the dislocations. The results show that after the solidification relaxation, the interfacial dislocations on both sides of the grain are distributed in parallel but opposite direction. With the increase of misorientation angle between grains, the number of dislocations increases, the spacing between them decreases, and the free energy of the system increases. Imposed by the applied strain, the grain boundary dislocations undergo climbing, launching, and reactive annihilation, with the free energy fluctuating. When the misorientation increases, the dislocation motion mode changes from climbing to climbing-sliping, resulting in more dislocation group configurations, and more reactions between dislocations and dislocation groups. For the dislocation reactions of different configurations, positive shear strain drives dislocations to approach, and negative shear strain drives dislocations to annihilate.
-
Keywords:
- phase field crystal /
- square phase /
- dislocation reaction /
- grain boundary
[1] Elder K R, Katakowski M, Haataja M, Grant M 2002 Phys. Rev. Lett. 88 245701
Google Scholar
[2] Elder K R, Grant M 2004 Phys. Rev. E 70 051605
Google Scholar
[3] Elder K R, Provatas N, Berry J, Stefanovic P, Grant M 2007 Phys. Rev. B 75 064107
Google Scholar
[4] 高英俊, 罗志荣, 黄创高, 卢强华, 林葵 2013 62 050507
Google Scholar
Gao Y J, Luo Z R, Huang C G, Lu Q H, Lin K 2013 Acta Phys. Sin. 62 050507
Google Scholar
[5] Yang T, Gao Y, Wang D, Shi R P, Chen Z, Nie J F, Li J, Wang Y 2017 Acta Mater. 127 481
Google Scholar
[6] Greenwood M, Rottler J, Provatas N 2011 Phys. Rev. E 83 031601
Google Scholar
[7] Gao Y J, Deng Q Q, Liu Z Y, Huang Z J, Li Y X, Luo Z R 2020 J. Mater. Sci. Technol. 49 236
Google Scholar
[8] Gao Y J, Huang L L, Deng Q Q, Zhou W Q, Luo Z R, Lin K 2016 Acta Mater. 117 238
Google Scholar
[9] 赵宇龙, 陈铮, 龙建, 杨涛 2013 62 118102
Google Scholar
Zhao Y L, Chen Z, Long J, Yang T 2013 Acta Phys. Sin. 62 118102
Google Scholar
[10] 赵宇龙, 陈铮, 龙建, 杨涛 2014 金属学报 27 81
Google Scholar
Zhao Y L, Chen Z, Long J, Yang T 2014 Acta Metall. Sin. 27 81
Google Scholar
[11] Gao Y J, Luo Z R, Huang L L, Mao H, Huang C G, Lin K 2016 Modell. Simul. Mater. Sci. 24 055010
Google Scholar
[12] Hu S, Chen Z, Xi W, Peng Y Y 2017 J. Mater. Sci. 52 5641
Google Scholar
[13] Seymour M, Sanches F, Elder K, Provatas N 2015 Phys. Rev. B 92 184109
Google Scholar
[14] Faghihi N, Provatas N, Elder K R, Grant M, Karttunen M 2013 Phys. Rev. E 88 032407
Google Scholar
[15] Berghoff M, Nestler B 2015 Comput. Condens. Matter 4 46
Google Scholar
[16] Tang S, Wang Z J, Guo Y L, et al. 2012 Acta Mater. 60 5501
Google Scholar
[17] 高英俊, 卢成健, 黄礼琳, 罗志荣, 黄创高 2014 金属学报 50 110
Google Scholar
Gao Y J, Lu C J, Huang L L, Luo Z R, Huang C G 2014 Acta Metall. Sin. 50 110
Google Scholar
[18] Hu S, Chen Z, Yu G G, Xi W, Peng Y Y 2016 Comput. Mater. Sci. 124 195
Google Scholar
[19] Gutkin M Y, Ovid'ko I A 2001 Phys. Rev. B 63 064515
Google Scholar
[20] Stefanovic P, Haataja M, Provatas N 2009 Phys. Rev. E 80 046107
Google Scholar
[21] Bobylev S V, Gutkin M Y, Ovid'ko I A 2004 Phys. Solid State 46 2053
Google Scholar
[22] Ohno T, Ii S, Shibata N, Matsunaga K, Ikuhara Y, Yamamoto T 2004 Mater. Trans. 45 2117
Google Scholar
[23] Humphreys F J 2001 J. Mater. Sci. 36 3833
Google Scholar
[24] Hirouchi T, Takaki T, Tomita Y 2009 Comput. Mater. Sci. 44 1192
Google Scholar
[25] 龙建, 王诏玉, 赵宇龙, 龙清华, 杨涛, 陈铮 2013 62 218101
Google Scholar
Long J, Wang Z Y, Zhao Y L, Long Q H, Yang T, Chen Z 2013 Acta Phys. Sin. 62 218101
Google Scholar
[26] 鲁娜, 王永欣, 陈铮 2014 63 180508
Google Scholar
Lu N, Wang Y X, Chen Z 2014 Acta Phys. Sin. 63 180508
Google Scholar
[27] 杨涛, 陈铮, 董伟平 2011 金属学报 47 1301
Google Scholar
Yang T, Chen Z, Dong W P 2011 Acta Metall. Sin. 47 1301
Google Scholar
[28] Berkels B, Ratz A, Rumpf M, Voigt A 2008 J. Sci. Comput. 35 1
Google Scholar
[29] Elsey M, Wirth B 2014 Multiscale Model. Sim. 12 1
Google Scholar
[30] Singer H M, Singer I 2006 Phys. Rev. E 74 031103
Google Scholar
[31] Wang Z J, Li J J, Guo Y L, Tang S, Wang J C 2013 Comput. Phys. Commun. 184 2489
Google Scholar
[32] Hytch M J, Snoeck E, Kilaas R 1998 Ultramicroscopy 74 131
Google Scholar
[33] Galindo P L, Kret S, Sanchez A M, et al. 2007 Ultramicroscopy 107 1186
Google Scholar
[34] Hytch M J, Putaux J L, Penisson J M 2003 Nature 423 270
Google Scholar
[35] Guo Y, Wang J, Wang Z, Li J, Tang S, Liu F, Zhou Y 2015 Philos. Mag. 95 973
Google Scholar
[36] Wu K A, Adland A, Karma A 2010 Phys. Rev. E 81 061601
Google Scholar
[37] Chen L Q, Shen J 1998 Comput. Phys. Commun. 108 147
Google Scholar
-
图 1 二维四方相相图(黑色部分为两相共存区)
Fig. 1. Phase diagram of the two-dimensional square lattices (the black part is the two-phase coexistence region).
图 2
$ \theta ={4} $ °时双晶弛豫过程的模拟 (a) t = 100; (b) t = 1300; (c) t = 1700; (d) t = 30000Fig. 2. Simulation of the relaxation process of bicrystals with
$ \theta ={4} $ °: (a) t = 100; (b) t = 1300; (c) t = 1700; (d) t = 30000.
图 3 不同取向差对应的位错构型、位错数目与位错间距
Fig. 3. Dislocation configuration, number of dislocations and dislocation distance corresponding to different misorientations.
图 4 取向差对弛豫过程体系自由能变化的影响
Fig. 4. Effect of misorientations on the change of free energy during relaxation process.
图 5 不同取向差下晶界处
$ {\varepsilon }_{xx} $ 应变云图 (a)$ \theta ={4} $ °; (b)$ \theta ={6} $ °; (c)$ \theta ={8} $ °Fig. 5. Contours of
$ {\varepsilon }_{xx} $ strain at the grain boundary under different misorientations: (a)$ \theta ={4} $ °; (b)$ \theta ={6} $ °; (c)$ \theta ={8} $ °.
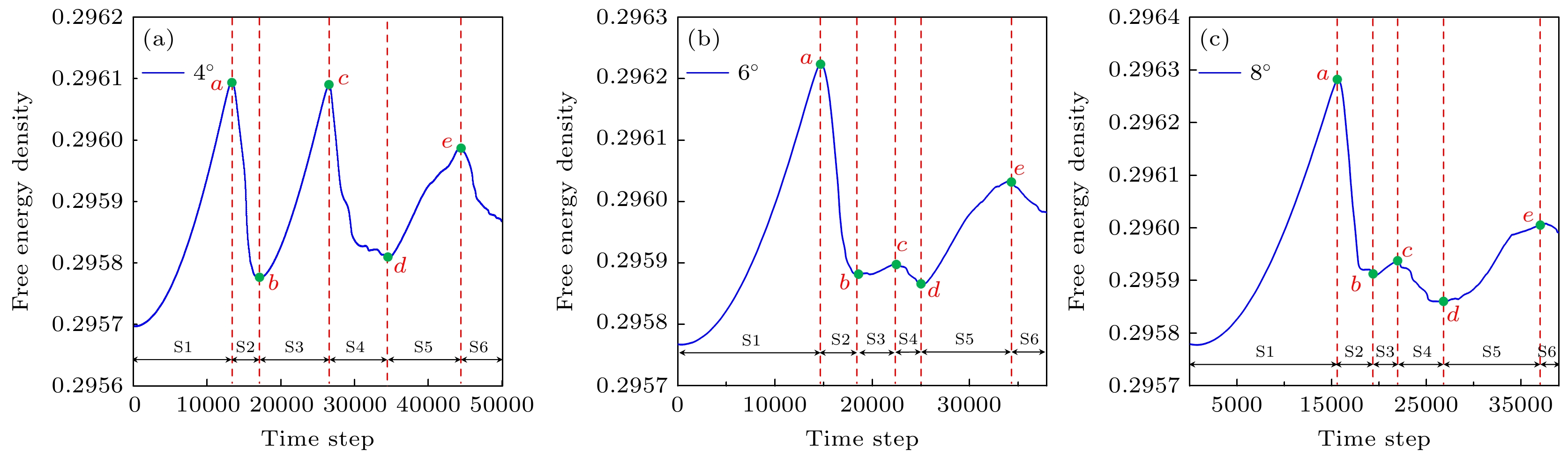
图 6 应变作用下
$ \theta ={4} $ °时晶界位错运动模拟图 (a) t = 50; (b) t = 14150; (c) t = 15250; (d) t = 17550; (e) t = 29100; (f) t = 48500. 图6(a)中插图(g)和(h)分别表示刃位错的类型和位错对应的伯氏矢量类型Fig. 6. Simulation of grain boundary dislocation motion under strain with
$ \theta ={4} $ °: (a) t = 50; (b) t = 14150; (c) t = 15250; (d) t = 17550; (e) t = 29100; (f) t = 48500. Inset (g) and (h) represent the type of edge dislocation and the Burgers vector type respectively corresponding to the dislocation in Fig. 6(a).
图 7 应变作用下
$ \theta ={6} $ °时晶界位错运动模拟图 (a) t = 50; (b) t = 15000; (c) t = 16350; (d) t = 19550; (e) t = 23500; (f) t = 26950Fig. 7. Simulation of grain boundary dislocation motion under strain with
$ \theta ={6} $ °: (a) t = 50; (b) t = 15000; (c) t = 16350; (d) t = 19550; (e) t = 23500; (f) t = 26950.
图 8 应变作用下
$ \theta ={8} $ °时晶界位错运动模拟图 (a) t = 100; (b) t = 16350; (c) t = 17500; (d) t = 20400; (e) t = 25000; (f) t = 34750Fig. 8. Simulation of grain boundary dislocation motion under strain with
$ \theta ={8} $ °: (a) t = 100; (b) t = 16350; (c) t = 17500; (d) t = 20400; (e) t = 25000; (f) t = 34750.
图 9 不同取向差下体系自由能变化曲线 (a)
$ \theta ={4}$ °; (b)$ \theta ={6} $ °; (c)$ \theta ={8} $ °Fig. 9. Variations of free energy under different misorientations: (a)
$ \theta ={4} $ °; (b)$ \theta ={6} $ °; (c)$ \theta ={8} $ °.
图 10 含位错组的晶体位错构型及对应的不同应变取向应变云图 (a) 晶体构型图; (b)
${\varepsilon }_{xx}$ ; (c)${\varepsilon }_{xy}$ ; (d)${\varepsilon }_{yy}$ Fig. 10. Dislocation configuration of crystals containing dislocation groups and corresponding strain contours of different strain orientations: (a) Crystal configuration diagram; (b)
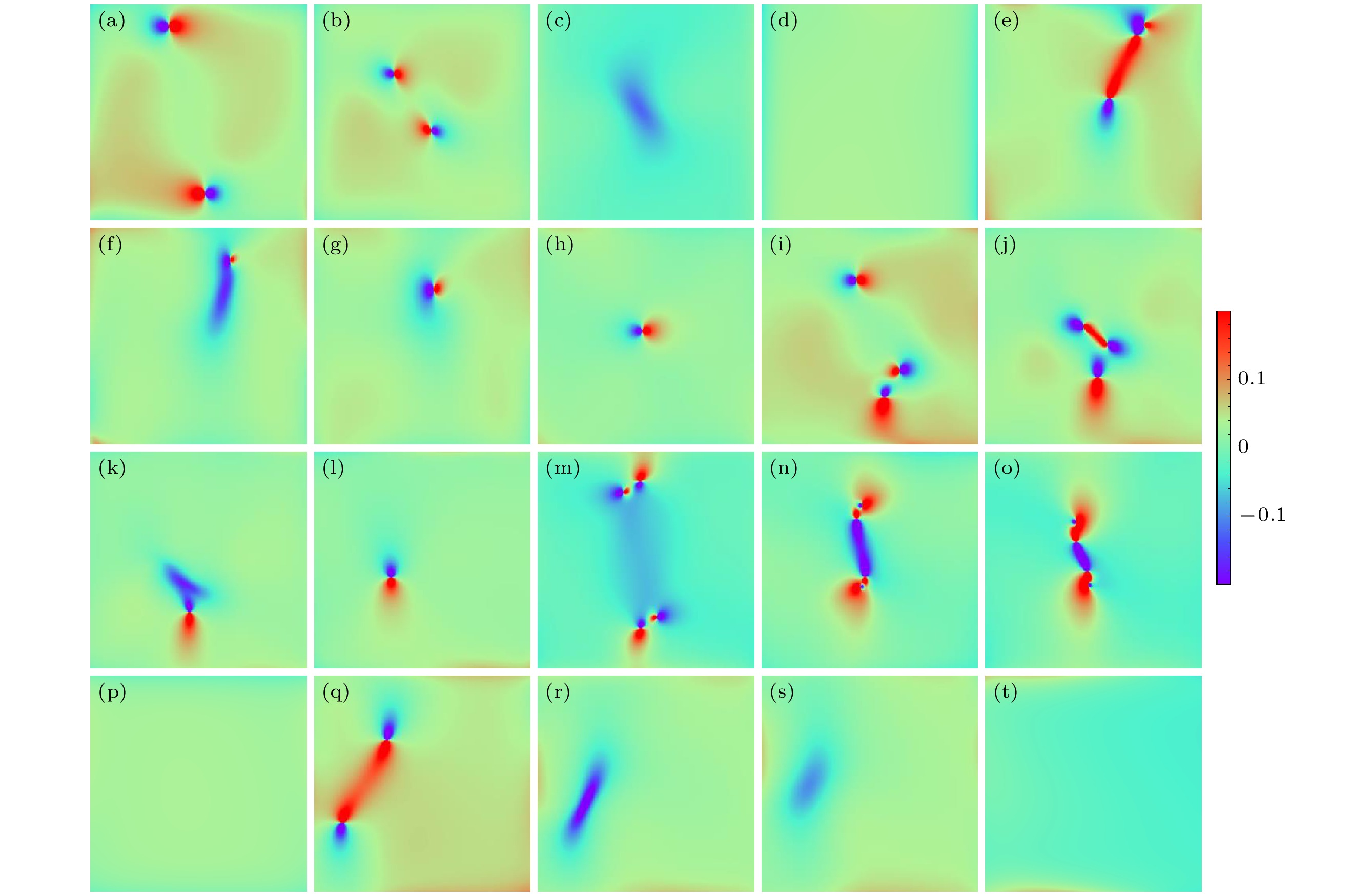
${\varepsilon }_{xx}$ ; (c)${\varepsilon }_{xy}$ ; (d)${\varepsilon }_{yy}$ .
图 11 不同位错反应构型的演化图 (a)—(d) R1构型; (e)—(h) R2构型; (i)—(l) R3构型; (m)—(p) R4构型; (q)—(t) R5构型
Fig. 11. Evolution of different dislocation reaction configurations: (a)–(d) R1 configurations; (e)–(h) R2 configurations; (i)–(l) R3 configurations; (m)–(p) R4 configurations; (q)–(t) R5 configurations.
图 12 不同位错反应构型演化时应变(
${\varepsilon }_{xy}$ )云图 (a)—(d) R1构型; (e)—(h) R2构型; (i)—(l) R3构型; (m)—(p) R4构型; (q)—(t) R5构型Fig. 12. Strain (
${\varepsilon }_{xy}$ ) contours during the evolution of different dislocation reaction configurations: (a)–(d) R1 configuration; (e)–(h) R2 configuration; (i)–(l) R3 configuration; (m)–(p) R4 configuration; (q)–(t) R5 configuration.表 1 模拟设定的参数
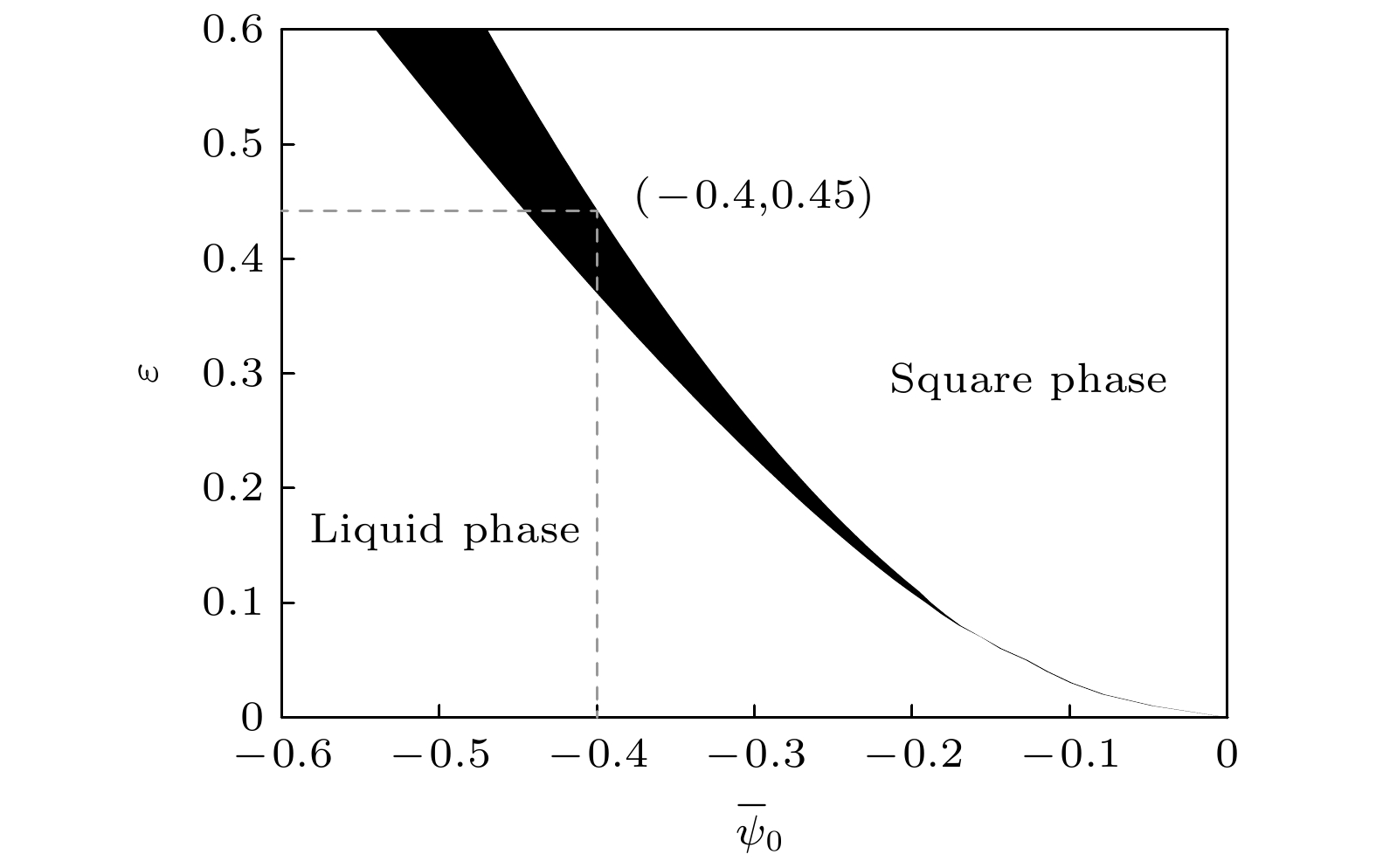
Table 1. Parameters in the simulation.
方案 初始原子密度$ {\overline \psi _0} $ 温度相关参量ε 取向差θ A $－0.40$ $ 0.45 $ $ {4} $° B $－0.40$ $ 0.45 $ $ {6} $° C $－0.40$ $ 0.45 $ $ {8} $° 
下载: 导出CSV
表 2 不同构型的位错分解发射与位错反应
Table 2. Dislocation decomposition and dislocation reaction of different configuration.
编号 位错分解发射 编号 位错反应 L1 $n1\xrightarrow{\text{分解}}n1+n3+n4$ R1 $ n3+n4\xrightarrow{\text{反应}} 0 $ $ n2 \xrightarrow{\text{分解}} n2+n3+n4 $ R2 $n1+\overline{n2 n4}\xrightarrow{\text{反应} }n4,$
$n2+\overline{n2 n3}\xrightarrow{\text{反应}}n4$L2 $n1\xrightarrow{\text{分解}}\overline{n1 n3}+n4$ R3 $n3+\overline{n2 n4}\xrightarrow{\text{反应} }n2,$
$n4+\overline{n1 n3}\xrightarrow{\text{反应}}n1$$n2\xrightarrow{\text{分解}}\overline{n2 n3}+n4$ R4 $\overline{n1 n3}+\overline{n2 n4}\xrightarrow{\text{反应} }0,$
$\overline{n1 n4}+\overline{n2 n3}\xrightarrow{\text{反应}}0$L3 $n1\xrightarrow{\text{分解}}\overline{n1 n4}+n3$ R5 $ n1+n2\xrightarrow{\text{反应}}0 $ $n2\xrightarrow{\text{分解}}\overline{n2 n4}+n3$
下载: 导出CSV
-
[1] Elder K R, Katakowski M, Haataja M, Grant M 2002 Phys. Rev. Lett. 88 245701
Google Scholar
[2] Elder K R, Grant M 2004 Phys. Rev. E 70 051605
Google Scholar
[3] Elder K R, Provatas N, Berry J, Stefanovic P, Grant M 2007 Phys. Rev. B 75 064107
Google Scholar
[4] 高英俊, 罗志荣, 黄创高, 卢强华, 林葵 2013 62 050507
Google Scholar
Gao Y J, Luo Z R, Huang C G, Lu Q H, Lin K 2013 Acta Phys. Sin. 62 050507
Google Scholar
[5] Yang T, Gao Y, Wang D, Shi R P, Chen Z, Nie J F, Li J, Wang Y 2017 Acta Mater. 127 481
Google Scholar
[6] Greenwood M, Rottler J, Provatas N 2011 Phys. Rev. E 83 031601
Google Scholar
[7] Gao Y J, Deng Q Q, Liu Z Y, Huang Z J, Li Y X, Luo Z R 2020 J. Mater. Sci. Technol. 49 236
Google Scholar
[8] Gao Y J, Huang L L, Deng Q Q, Zhou W Q, Luo Z R, Lin K 2016 Acta Mater. 117 238
Google Scholar
[9] 赵宇龙, 陈铮, 龙建, 杨涛 2013 62 118102
Google Scholar
Zhao Y L, Chen Z, Long J, Yang T 2013 Acta Phys. Sin. 62 118102
Google Scholar
[10] 赵宇龙, 陈铮, 龙建, 杨涛 2014 金属学报 27 81
Google Scholar
Zhao Y L, Chen Z, Long J, Yang T 2014 Acta Metall. Sin. 27 81
Google Scholar
[11] Gao Y J, Luo Z R, Huang L L, Mao H, Huang C G, Lin K 2016 Modell. Simul. Mater. Sci. 24 055010
Google Scholar
[12] Hu S, Chen Z, Xi W, Peng Y Y 2017 J. Mater. Sci. 52 5641
Google Scholar
[13] Seymour M, Sanches F, Elder K, Provatas N 2015 Phys. Rev. B 92 184109
Google Scholar
[14] Faghihi N, Provatas N, Elder K R, Grant M, Karttunen M 2013 Phys. Rev. E 88 032407
Google Scholar
[15] Berghoff M, Nestler B 2015 Comput. Condens. Matter 4 46
Google Scholar
[16] Tang S, Wang Z J, Guo Y L, et al. 2012 Acta Mater. 60 5501
Google Scholar
[17] 高英俊, 卢成健, 黄礼琳, 罗志荣, 黄创高 2014 金属学报 50 110
Google Scholar
Gao Y J, Lu C J, Huang L L, Luo Z R, Huang C G 2014 Acta Metall. Sin. 50 110
Google Scholar
[18] Hu S, Chen Z, Yu G G, Xi W, Peng Y Y 2016 Comput. Mater. Sci. 124 195
Google Scholar
[19] Gutkin M Y, Ovid'ko I A 2001 Phys. Rev. B 63 064515
Google Scholar
[20] Stefanovic P, Haataja M, Provatas N 2009 Phys. Rev. E 80 046107
Google Scholar
[21] Bobylev S V, Gutkin M Y, Ovid'ko I A 2004 Phys. Solid State 46 2053
Google Scholar
[22] Ohno T, Ii S, Shibata N, Matsunaga K, Ikuhara Y, Yamamoto T 2004 Mater. Trans. 45 2117
Google Scholar
[23] Humphreys F J 2001 J. Mater. Sci. 36 3833
Google Scholar
[24] Hirouchi T, Takaki T, Tomita Y 2009 Comput. Mater. Sci. 44 1192
Google Scholar
[25] 龙建, 王诏玉, 赵宇龙, 龙清华, 杨涛, 陈铮 2013 62 218101
Google Scholar
Long J, Wang Z Y, Zhao Y L, Long Q H, Yang T, Chen Z 2013 Acta Phys. Sin. 62 218101
Google Scholar
[26] 鲁娜, 王永欣, 陈铮 2014 63 180508
Google Scholar
Lu N, Wang Y X, Chen Z 2014 Acta Phys. Sin. 63 180508
Google Scholar
[27] 杨涛, 陈铮, 董伟平 2011 金属学报 47 1301
Google Scholar
Yang T, Chen Z, Dong W P 2011 Acta Metall. Sin. 47 1301
Google Scholar
[28] Berkels B, Ratz A, Rumpf M, Voigt A 2008 J. Sci. Comput. 35 1
Google Scholar
[29] Elsey M, Wirth B 2014 Multiscale Model. Sim. 12 1
Google Scholar
[30] Singer H M, Singer I 2006 Phys. Rev. E 74 031103
Google Scholar
[31] Wang Z J, Li J J, Guo Y L, Tang S, Wang J C 2013 Comput. Phys. Commun. 184 2489
Google Scholar
[32] Hytch M J, Snoeck E, Kilaas R 1998 Ultramicroscopy 74 131
Google Scholar
[33] Galindo P L, Kret S, Sanchez A M, et al. 2007 Ultramicroscopy 107 1186
Google Scholar
[34] Hytch M J, Putaux J L, Penisson J M 2003 Nature 423 270
Google Scholar
[35] Guo Y, Wang J, Wang Z, Li J, Tang S, Liu F, Zhou Y 2015 Philos. Mag. 95 973
Google Scholar
[36] Wu K A, Adland A, Karma A 2010 Phys. Rev. E 81 061601
Google Scholar
[37] Chen L Q, Shen J 1998 Comput. Phys. Commun. 108 147
Google Scholar
下载:
计量
- 文章访问数: 4481
- PDF下载量: 70
- 被引次数: 0
