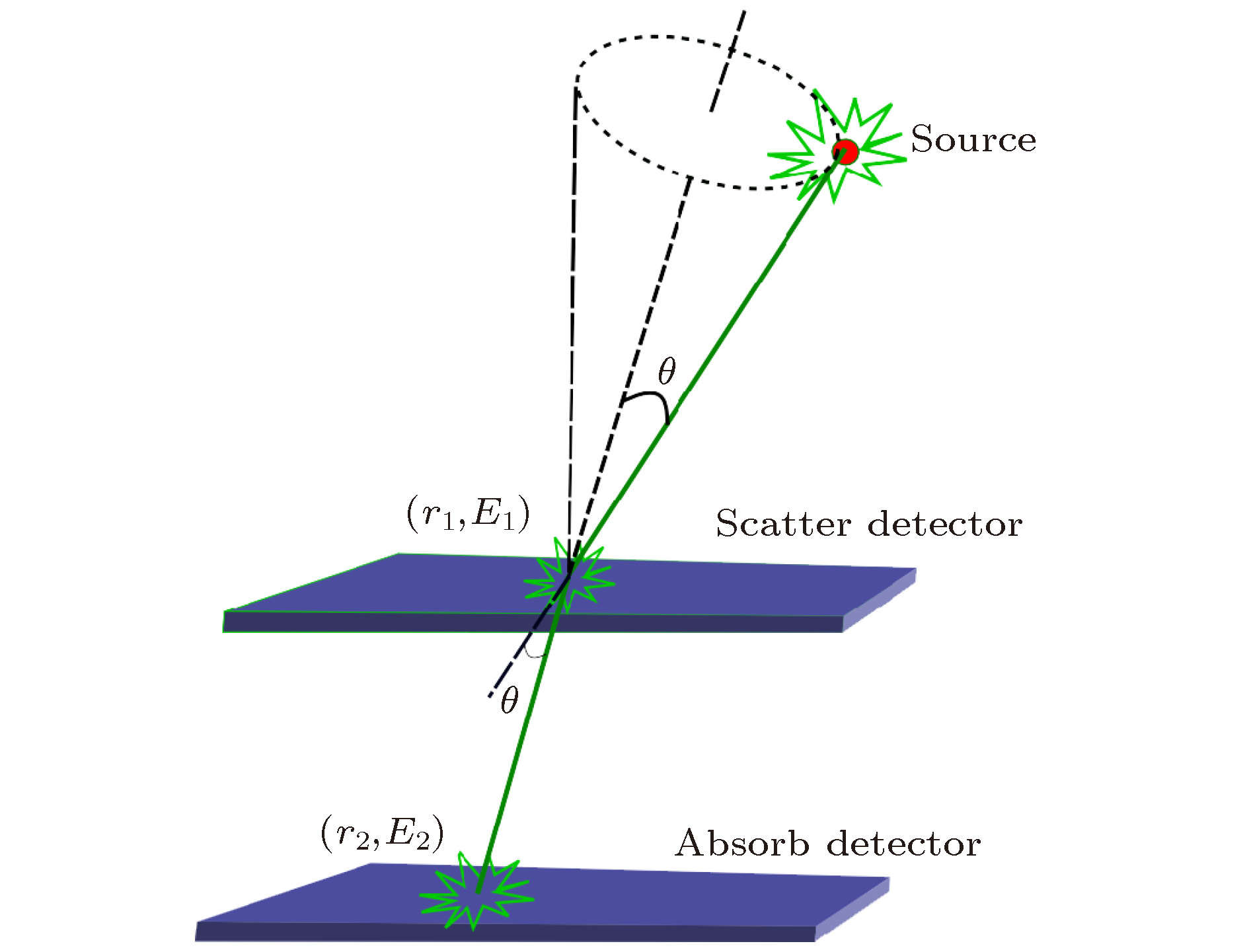
-
Compared with traditional gamma-ray imaging equipment, the Compton camera is a very promising imaging device in nuclear medicine and molecular imaging, and has a strong potential application in monitoring beams in heavy-ion-therapy because of its high efficiency feature. A demonstration device for heavy ion cancer treatment with complete intellectual property right has been built at Institute of Modern Physics, Chinese Academy of Sciences in Wuwei city of Gansu Province. At present the device is being up-graded, and the heavy ion cancer treatment is being generalized in national wide. In view of the broad prospects of heavy ion cancer treatment, the imaging resolution of Compton camera is analyzed theoretically, and three errors effecting the imaging resolution, which are energy resolution, position resolution of detector and the Doppler effect, are determined. Then the three errors are simulated by using the Geant 4 packages. The physical process in simulation is selected as the G4EMPenelopePhysics model, which makes the atomic shell cross section data for low energy physical process used directly. The Compton camera geometry consists of two layers of detectors. The layer close to
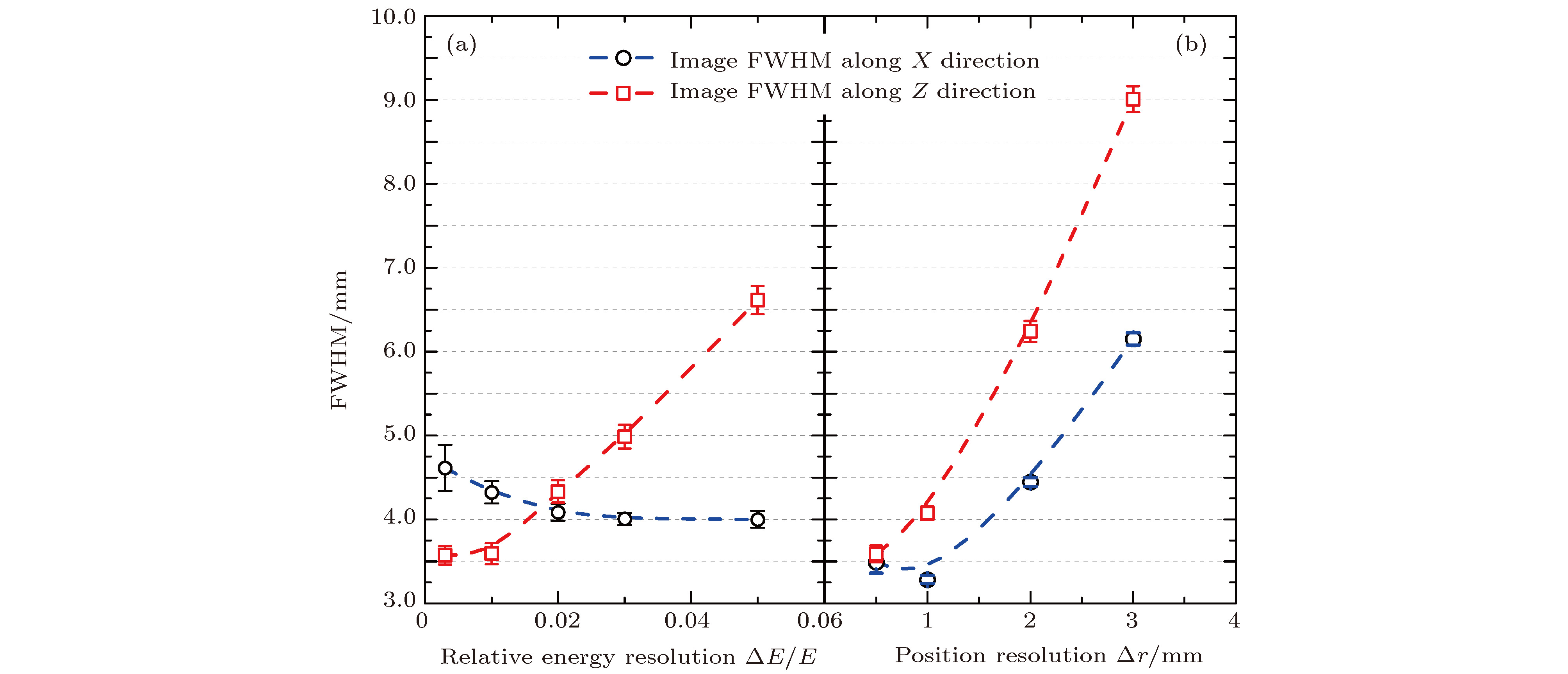
$\gamma$ source is called detector and the other one is called absorption detector. The material of scatter detector is selected as low-Z silicon and carbon, and the absorb detector is high-Z germanium. The thickness value of scatter detector and absorb detector are both 20 mm. The spacing between the two layers is 100 mm. The simulation results by Geant 4 are used to reconstruct the image of point-like$\gamma$ source through using the back-projection algorithm. The simulation results and the re-constructed images indicate that the difference between the image full width at half maximum induced by 2 mm position resolution and that induced by 5.0% relative energy resolution of scatter detector is about 10%, and amount to that by the Doppler effect of Silicon. For the$\gamma$ ray with energies of several hundred keV, the energy resolution of Si detectors is easily better than 1.0% in practice. Therefore, the detector's position resolution dominates the image quality of the Compton camera. Considering the Doppler effect, manufacturing techniques and imaging efficiency, 2.0 mm-sized crystal unit and 1.0% energy resolution power is suggested for practically manufacturing the Compton camera.-
Keywords:
- Compton camera /
- heavy ion therapy /
- Geant 4 simulation /
- back-projection imaging
[1] Parodi K 2016 Nucl. Instrum. Meth. A 809 113
Google Scholar
[2] Shakirin G, Braess H, Fiedler F, et al. 2011 Phys. Med. Biol. 56 1281
Google Scholar
[3] Enghardt W, Crespo P, Fiedler F, et al. 2004 Nucl. Instrum. Meth. A 525 284
Google Scholar
[4] Nishio T, Ogino T, Nomura K, et al. 2006 Med. Phys. 33 4190
Google Scholar
[5] Amaldi U, Hajdas W, Iliescu S, et al. 2010 Nucl. Instrum. Meth. A 617 248
Google Scholar
[6] Henriquet P, Testa E, Chevallier M, et al. 2012 Phys. Med. Biol. 57 4655
Google Scholar
[7] Agodi C, Battistoni G, Bellini F, et al. 2012 Phys. Med. Biol. 57 5667
Google Scholar
[8] Gwosch K, Hartmann B, Jakubek J, et al. 2013 Phys. Med. Biol. 58 3755
Google Scholar
[9] Borm V, Joulaeizadeh L, Beekman F, et al. 2012 Phys. Med. Biol. 57 297
Google Scholar
[10] Testa M, Bajard M, Chevallier M, et al. 2010 Radiat. Environ. Biophy. 49 337
Google Scholar
[11] Krimmer J, Ley J L, Abellan C, et al. 2015 Nucl. Instrum. Meth. A 787 98
Google Scholar
[12] Peterson S W, Robertson D, Polf J, et al. 2010 Phys. Med. Biol. 55 6841
Google Scholar
[13] Seo H, Park J H, Ushakov A, et al. 2011 J. Instrum. 6 C01024
[14] Kurosawa S, Kubo H, Ueno K, et al. 2012 Curr. Appl. Phys. 12 364
Google Scholar
[15] Kormoll T, Fiedler F, Schone S, et al. 2011 Nucl. Instrum. Meth. A 626−627 114
Google Scholar
[16] Llosa G, Cabello J, Callier S, et al. 2013 Nucl. Instrum. Meth. A 718 130
Google Scholar
[17] Schoenfelder V, Himer A, Schneider K, et al. 1973 Nucl. Instrum. Meth. 107 385
Google Scholar
[18] Todd R W, Nightingale J M, Everett D B, et al. 1974 Nature 251 132
Google Scholar
-
图 1 康普顿相机成像原理示意图
Figure 1. Sketch of imaging principle of a Compton camera.
图 3 康普顿散射角不确定度
$ \Delta\theta_{\rm E} $ 分布的模拟结果, 相对能量分辨为1.0%, 初始$\gamma$ 射线能量分别为100 和1000 keVFigure 3. Simulated distribution of
$ \Delta\theta_{\rm E} $ . The relative energy resolution is fitted to 1.0%, the initial$\gamma$ -ray energy is 100 and 1000 keV, respectively.
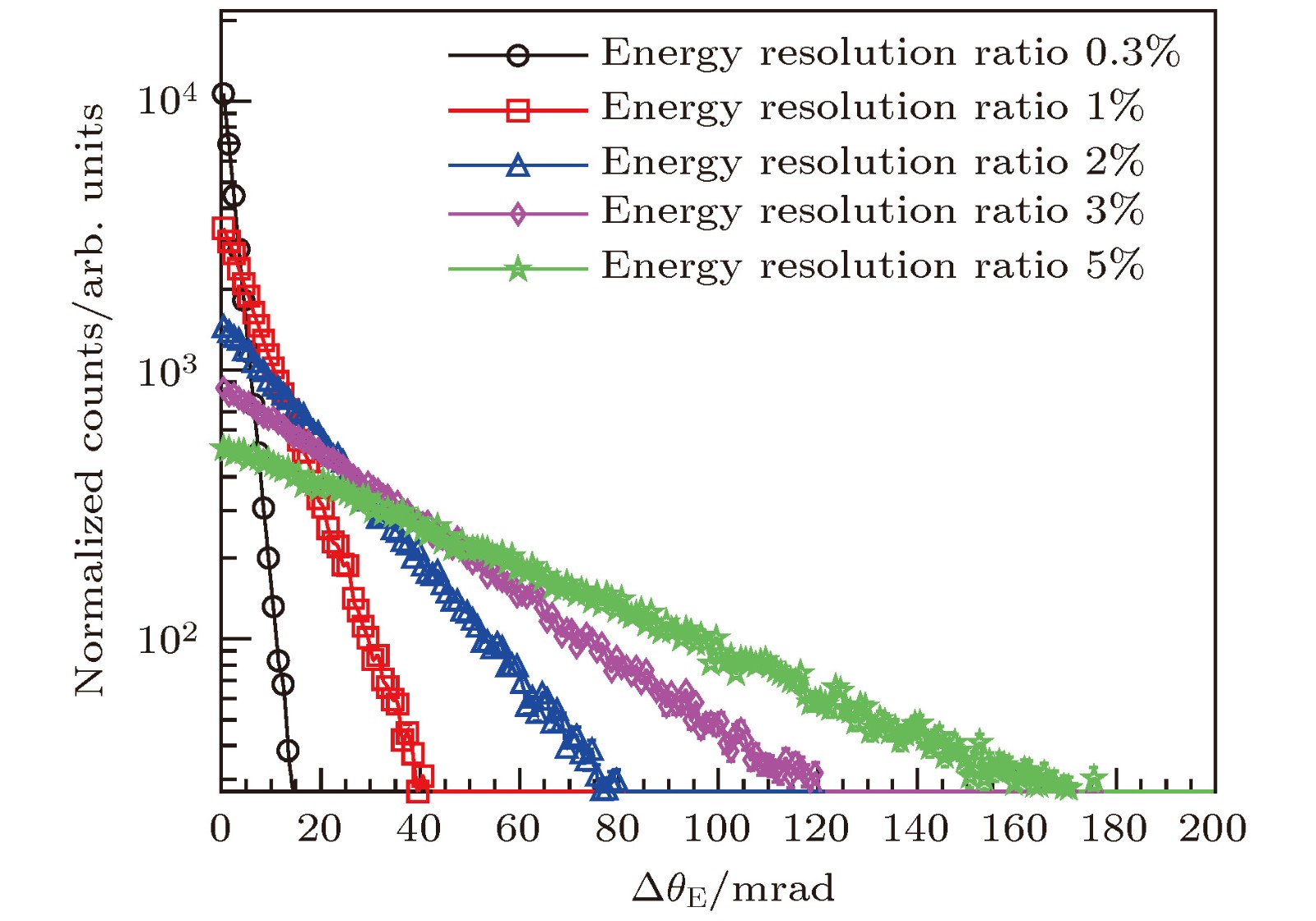
图 2 康普顿相机的能量分辨本领引起的康普顿散射角不确定度
$ \Delta\theta_{\rm E} $ 分布的模拟结果, 相对能量分辨$\Delta E/E$ 取值从0.3%至5%, 初始$\gamma$ 射线能量为600 keVFigure 2. Simulated distribution of the uncertainty of Compton scattering angle caused by the resolving power of Compton camera. The value of
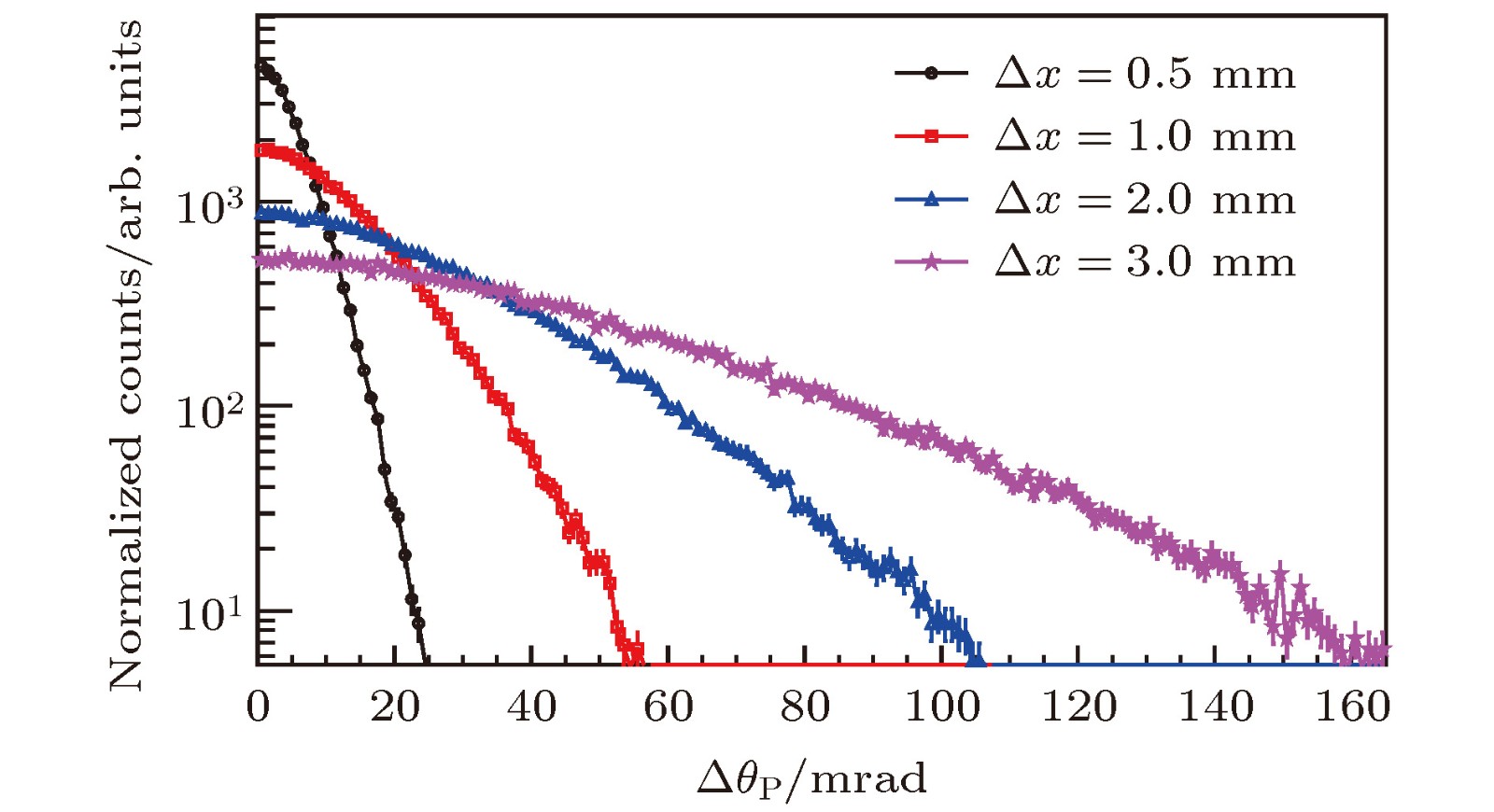
$\Delta E/E$ is from 0.3% to 5%. The initial$\gamma$ -ray energy is 600 keV.
图 4 康普顿相机的位置分辨本领引起的康普顿散射角不确定度
$ \Delta\theta_{\rm P} $ 分布的模拟结果, 位置分辨$\Delta x$ 取值范围为0.5—3.0 mm. 初始$\gamma$ 射线能量为600 keVFigure 4. Simulated distribution of the uncertainty of Compton scattering angle caused by the position resolving power of Compton camera. The value of
$\Delta x$ is from 0.5 mm to 3.0 mm. The initial$\gamma$ -ray energy is 600 keV.
图 5 康普顿散射角不确定度
$ \Delta\theta_{\rm C} $ 分布的模拟结果, 初始$\gamma$ 射线能量为600 keV, 散射材料分别为C和SiFigure 5. Simulated distribution of
$ \Delta\theta_{\rm C} $ . The initial$\gamma$ ray energy is 600 keV. The material of scattering detector is C and Si, respectively.
图 7 当散射探测器的位置分辨为2.0 mm时, 对
$\gamma$ 点源的反投影重建图像Figure 7. Image of point-like gamma source reconstructed by back-projection algorithm as position resolution of scatter detector is 2.0 mm.
图 6 当散射探测器的相对能量分辨为1.0%时, 对
$\gamma$ 点源的反投影重建图像Figure 6. Image of point-like gamma source reconstructed by back-projection algorithm as relative energy resolution of scatter detector is 1.0%.
图 8 反投影法重建图像的FWHM随散射探测器分辨本领的变化 (a) 随相对能量分辨; (b) 随位置分辨
Figure 8. FWHM for
$\gamma$ image reconstructed by back-projection algorithm vs. (a) relative energy and (b) position resolution of scatter detector.
图 9 只包含散射材料(Si晶体)的多普勒效应时, 对
$\gamma$ 点源的反投影重建图像Figure 9. Image of point-like gamma source reconstructed by back-projection algorithm only including the Doppler effect of electrons bounded in scatter material.
-
[1] Parodi K 2016 Nucl. Instrum. Meth. A 809 113
Google Scholar
[2] Shakirin G, Braess H, Fiedler F, et al. 2011 Phys. Med. Biol. 56 1281
Google Scholar
[3] Enghardt W, Crespo P, Fiedler F, et al. 2004 Nucl. Instrum. Meth. A 525 284
Google Scholar
[4] Nishio T, Ogino T, Nomura K, et al. 2006 Med. Phys. 33 4190
Google Scholar
[5] Amaldi U, Hajdas W, Iliescu S, et al. 2010 Nucl. Instrum. Meth. A 617 248
Google Scholar
[6] Henriquet P, Testa E, Chevallier M, et al. 2012 Phys. Med. Biol. 57 4655
Google Scholar
[7] Agodi C, Battistoni G, Bellini F, et al. 2012 Phys. Med. Biol. 57 5667
Google Scholar
[8] Gwosch K, Hartmann B, Jakubek J, et al. 2013 Phys. Med. Biol. 58 3755
Google Scholar
[9] Borm V, Joulaeizadeh L, Beekman F, et al. 2012 Phys. Med. Biol. 57 297
Google Scholar
[10] Testa M, Bajard M, Chevallier M, et al. 2010 Radiat. Environ. Biophy. 49 337
Google Scholar
[11] Krimmer J, Ley J L, Abellan C, et al. 2015 Nucl. Instrum. Meth. A 787 98
Google Scholar
[12] Peterson S W, Robertson D, Polf J, et al. 2010 Phys. Med. Biol. 55 6841
Google Scholar
[13] Seo H, Park J H, Ushakov A, et al. 2011 J. Instrum. 6 C01024
[14] Kurosawa S, Kubo H, Ueno K, et al. 2012 Curr. Appl. Phys. 12 364
Google Scholar
[15] Kormoll T, Fiedler F, Schone S, et al. 2011 Nucl. Instrum. Meth. A 626−627 114
Google Scholar
[16] Llosa G, Cabello J, Callier S, et al. 2013 Nucl. Instrum. Meth. A 718 130
Google Scholar
[17] Schoenfelder V, Himer A, Schneider K, et al. 1973 Nucl. Instrum. Meth. 107 385
Google Scholar
[18] Todd R W, Nightingale J M, Everett D B, et al. 1974 Nature 251 132
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 11556
- PDF Downloads: 222
- Cited By: 0
