-
As a new technique of photomicrography of complex optical field, the Fresnel incoherent correlation holography (FINCH) is particularly attractive in recent years because of its incoherent optical recording characteristics. For a new image recording and reconstruction system, a key concern is how to configure the experimental layout of FINCH by using available optical elements to achieve optimal resolution. However, in previous reports, there exist different viewpoints about this issue, and the imaging conditions of the best resolution remain to be clarified. As is well known, the imaging resolution is affected by the effective aperture of hologram and the change of the recording distance between spatial light modulator (SLM) and image sensor (CCD) can cause the hologram aperture to change. In the FINCH system the effective aperture of hologram is related not only to the aperture influence of each element used in the recording system, but also to the overlapping area of interference between the signal and reference wave and the pixel spacing of the image sensor. In previous reports, the researchers mainly used the ray-tracing method to discuss the effective aperture radius of hologram by ignoring the influences of the diffraction of light wave and the pixel spacing size of image sensor on the aperture of hologram. Based on the theories of wave optics we carry out a thorough investigation into the effective aperture of FINCH. We find that the pixelization of the image sensor, e.g. CCD, is a decisive factor influencing the resolution of FINCH, and we adopt numerical simulations and optical experiments to further verify the theoretical conclusions that the optimal lateral resolution of FINCH is achieved only if the recording distance (Zh) is equal to the focal length (fd) of diffractive lens displayed on a spatial light modulator; the resolution is deteriorated with the increase of
$\left| {{Z_{\rm{h}}} - {f_{\rm{d}}}} \right|$ . From the viewpoint of Fourier optics, the smaller the imaging distance$\left| {{Z_{\rm{h}}} - {f_{\rm{d}}}} \right|$ , the larger the aperture angle of hologram ($ \approx {{{R_{\rm{h}}}} / {\left| {{Z_{\rm{h}}} - {f_{\rm d}}} \right|}}$ ), the higher the collected spatial frequency is, hence, the higher the lateral resolution is. On the other hand, although the FINCH overcomes the spatial coherence limitation, it requires temporally coherent or quasi-monochromatic light. Our study also indicates that the requirements for the spatiotemporal coherence can be eased when the CCD is located at the focal plane of diffractive lens.-
Keywords:
- holography /
- resolution /
- zone plates /
- liquid-crystal devices
[1] Osten W, Faridian A, Gao P, Korner K, Naik D, Pedrini G, Singh A K, Takeda M, Wilke M 2014 Appl. Opt. 53 G44
Google Scholar
[2] Kreis T 2016 IEEE Trans. Ind. Infomat. 12 240
Google Scholar
[3] Kelner R, Rosen J 2016 IEEE Trans. Ind. Infomat. 12 220
Google Scholar
[4] Rosen J, Brooker G 2007 Opt. Lett. 32 912
Google Scholar
[5] Rosen J, Brooker G 2008 Nat. Photon. 2 190
Google Scholar
[6] Rosen J, Brooker G 2007 Opt. Express 15 2244
Google Scholar
[7] Lai X M, Zhao Y, Lv X H, Zhou Z Q, Zeng S Q 2012 Opt. Lett. 37 2445
Google Scholar
[8] Siegel N, Rosen J, Brooker G 2012 Opt. Express 20 19822
Google Scholar
[9] Katz B, Rosen J 2010 Opt. Express 18 962
Google Scholar
[10] Rosen J, Kelner R 2014 Opt. Express 22 29048
Google Scholar
[11] Katz B, Rosen J, Kelner R, Brooker G 2012 Opt. Express 20 9109
Google Scholar
[12] Wan Y H, Man T L, Chen H, Jiang Z Q, Wang D Y 2014 Chin. Phys. Lett. 31 044203
Google Scholar
[13] Siegel N, Rosen J, Brooker G 2013 Opt. Lett. 38 3922
Google Scholar
[14] Katz B, Wulich D, Rosen J 2010 Appl. Opt. 49 5757
Google Scholar
[15] Brooker G, Siegel N, Wang V, Rosen J 2011 Opt. Express 19 5047
Google Scholar
[16] Rosen J, Siegel N, Brooker G 2011 Opt. Express 19 26249
Google Scholar
[17] Bouchal P, Kapitan J, Chmelik R, Bouchal Z 2011 Opt. Express 19 15603
Google Scholar
[18] Vijayakumar A, Kashter Y, Kelner R, Rosen J 2017 Appl. Opt . 56 F67
Google Scholar
[19] 白云鹤, 臧瑞环, 汪盼, 荣腾达, 马凤英, 杜艳丽, 段智勇, 弓巧侠 2018 67 064202
Google Scholar
Bai Y H, Zang R H, Wang P, Rong T D, Ma F Y, Du Y L, Duan Z Y, Gong Q X 2018 Acta Phys. Sin. 67 064202
Google Scholar
[20] Goodman J W 1996 Introduction to Fourier Optics (New York: McGraw-Hill) pp66−67, p157
[21] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge: Cambridge University Press) pp128−144
[22] Kim M K 2011 Digital Holographic Microscopy: Principles, Techniques, and Applications (New York: Springer) pp63−64
[23] Claus D, Iliescu D, Rodenburg J M 2013 Appl. Opt. 52 A326
Google Scholar
[24] Sun P C, Leith E N 1994 Appl. Opt. 33 597
Google Scholar
[25] Yang G G, Chen H S, Leith E N 2000 Appl. Opt. 39 4076
Google Scholar
[26] Muffoletto R P, Tyler J M, Tohline J E 2007 Opt. Express 15 5631
Google Scholar
[27] Guo C S, Xie Y Y, Sha B 2014 Opt. Lett. 39 2338
Google Scholar
[28] Jacquot M, Sandoz P, Tribillon G 2001 Opt. Commun. 190 87
Google Scholar
[29] Cuche E, Marquet P, Depeursinge C 1999 Appl. Opt. 38 6994
Google Scholar
[30] Guo C S, Zhang L, Rong Z Y, Wang H T 2003 Opt. Eng. 42 2768
Google Scholar
-
图 1 FINCH系统原理示意图(P1和P2为偏振片)
Figure 1. Illustration of the principle of FINCH system, where P1 and P2 are polarizers.
图 2 可分辨物点半径
${\rho _{\rm{o}}}$ 与${Z_{\rm{h}}}$ 的相互依赖关系(${f_{\rm{d}}}{\rm{ = }}\;0.60\;{\rm{m}}$ ) (a)可分辨像斑半径${\rho _{\rm{o}}}$ 的数值模拟实验和解析计算的结果比较; (b)数值模拟的再现像斑的强度分布Figure 2. Dependence of the radius
${\rho _{\rm{o}}}$ of resolvable image spot on the recording distance${Z_{\rm{h}}}$ while keeping${f_{\rm{d}}}{\rm{ = }}\;0.60\;{\rm{m}}$ : (a) Comparisons between numerical simulation experiment and analytical calculation of resolvable speckle radius${\rho _{\rm{o}}};$ (b) intensity profiles of reconstructed image spots by numerical simulation.
图 3 不同记录距离
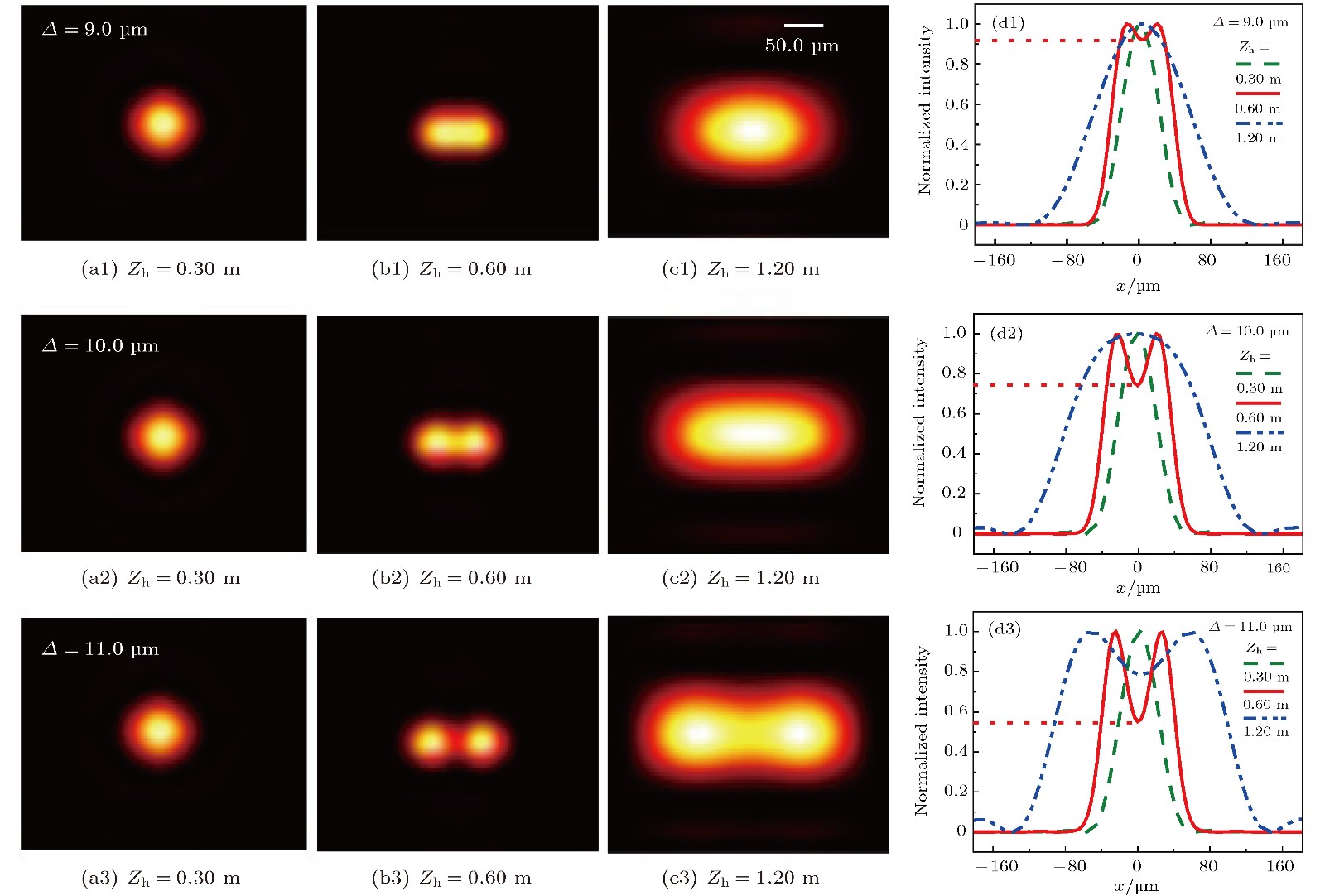
${Z_{\rm{h}}}$ (0.30 m (a), 0.60 m (b)和1.20 m (c))获得的双物点再现像, 其中${f_{\rm{d}}} = 0.60\;{\rm{m}}$ , 双物点间距$\varDelta $ 分别为$9.0$ (第1行),$10.0$ (第2行)和$11.0\; {\text{μ}} {\rm{m}}$ (第3行); (d1), (d2)和(d3)分别表示双物点间距$\varDelta $ 为9.0, 10.0和$11.0\; {\text{μ}} {\rm{m}}$ 时, 再现像强度的一维分布Figure 3. Reconstructed double images under different recording distances
${Z_{\rm{h}}}$ (0.30 m (a), 0.60 m (b) and 1.20 m (c)) while keeping${f_{\rm{d}}} = 0.60\;{\rm{m}}$ for different spacing of two object points$\varDelta = 9.0\;{\text{μ}} {\rm{m}}$ (the first row),$10.0\;{\text{μ}} {\rm{m}}$ (the second row) and$11.0\; {\text{μ}} {\rm{m}}$ (the third row), respectively. (d1), (d2) and (d3) One-dimensional distribution of reconstructed image intensity for$\varDelta = 9.0, 10.0$ and$11.0\; {\text{μ}} {\rm{m}}$ , respectively.
图 5 (a)计算机数字再现的图像, 其中对每一种衍射透镜焦距
${f_{\rm{d}}}$ (分别为0.30, 0.40, 0.50和0.60 m)测试了不同记录距离${Z_{\rm{h}}}$ (= 0.90${f_{\rm{d}}},$ 0.95${f_{\rm{d}}},$ 1.00${f_{\rm{d}}},$ 1.05${f_{\rm{d}}}$ , 1.10${f_{\rm{d}}}$ ); (b)不同的记录距离相对值(${{\alpha = {Z_{\rm{h}}}} / {{f_{\rm{d}}}}}$ )对应的再现像可见度Figure 5. (a) Computer digital reconstructed images for
${f_{\rm{d}}}$ = 0.30, 0.40, 0.50 and 0.60 m, each with different${Z_{\rm{h}}}$ (= 0.90${f_{\rm{d}}},$ 0.95${f_{\rm{d}}},$ 1.00${f_{\rm{d}}},$ 1.05${f_{\rm{d}}}$ and 1.10${f_{\rm{d}}}$ ); (b) relative values of different recording distances (${{\alpha = {Z_{\rm{h}}}} / {{f_{\rm{d}}}}}$ ) corresponding to visibility of reconstructed image.
图 6 (a)—(o) 再现图像的裁剪部分,
${f_{\rm{d}}} = 0.60\;{\rm{m}}$ , 记录距离${Z_{\rm{h}}}$ 从0.53 m到0.67 m, 红色框所标记区域的可见度将在图7中显示Figure 6. (a)−(o) Cropped sections of reconstructed images when
${Z_{\rm{h}}}$ varies from 0.53 m to 0.67 m while${f_{\rm{d}}}$ = 0.60 m. Visibility of the lines marked with the red box for the different${Z_{\rm{h}}}$ will be plotted in Figure 7.
图 4 FINCH系统光学实验装置示意图
Figure 4. Schematic representation of experimental set-up of FINCH.
-
[1] Osten W, Faridian A, Gao P, Korner K, Naik D, Pedrini G, Singh A K, Takeda M, Wilke M 2014 Appl. Opt. 53 G44
Google Scholar
[2] Kreis T 2016 IEEE Trans. Ind. Infomat. 12 240
Google Scholar
[3] Kelner R, Rosen J 2016 IEEE Trans. Ind. Infomat. 12 220
Google Scholar
[4] Rosen J, Brooker G 2007 Opt. Lett. 32 912
Google Scholar
[5] Rosen J, Brooker G 2008 Nat. Photon. 2 190
Google Scholar
[6] Rosen J, Brooker G 2007 Opt. Express 15 2244
Google Scholar
[7] Lai X M, Zhao Y, Lv X H, Zhou Z Q, Zeng S Q 2012 Opt. Lett. 37 2445
Google Scholar
[8] Siegel N, Rosen J, Brooker G 2012 Opt. Express 20 19822
Google Scholar
[9] Katz B, Rosen J 2010 Opt. Express 18 962
Google Scholar
[10] Rosen J, Kelner R 2014 Opt. Express 22 29048
Google Scholar
[11] Katz B, Rosen J, Kelner R, Brooker G 2012 Opt. Express 20 9109
Google Scholar
[12] Wan Y H, Man T L, Chen H, Jiang Z Q, Wang D Y 2014 Chin. Phys. Lett. 31 044203
Google Scholar
[13] Siegel N, Rosen J, Brooker G 2013 Opt. Lett. 38 3922
Google Scholar
[14] Katz B, Wulich D, Rosen J 2010 Appl. Opt. 49 5757
Google Scholar
[15] Brooker G, Siegel N, Wang V, Rosen J 2011 Opt. Express 19 5047
Google Scholar
[16] Rosen J, Siegel N, Brooker G 2011 Opt. Express 19 26249
Google Scholar
[17] Bouchal P, Kapitan J, Chmelik R, Bouchal Z 2011 Opt. Express 19 15603
Google Scholar
[18] Vijayakumar A, Kashter Y, Kelner R, Rosen J 2017 Appl. Opt . 56 F67
Google Scholar
[19] 白云鹤, 臧瑞环, 汪盼, 荣腾达, 马凤英, 杜艳丽, 段智勇, 弓巧侠 2018 67 064202
Google Scholar
Bai Y H, Zang R H, Wang P, Rong T D, Ma F Y, Du Y L, Duan Z Y, Gong Q X 2018 Acta Phys. Sin. 67 064202
Google Scholar
[20] Goodman J W 1996 Introduction to Fourier Optics (New York: McGraw-Hill) pp66−67, p157
[21] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge: Cambridge University Press) pp128−144
[22] Kim M K 2011 Digital Holographic Microscopy: Principles, Techniques, and Applications (New York: Springer) pp63−64
[23] Claus D, Iliescu D, Rodenburg J M 2013 Appl. Opt. 52 A326
Google Scholar
[24] Sun P C, Leith E N 1994 Appl. Opt. 33 597
Google Scholar
[25] Yang G G, Chen H S, Leith E N 2000 Appl. Opt. 39 4076
Google Scholar
[26] Muffoletto R P, Tyler J M, Tohline J E 2007 Opt. Express 15 5631
Google Scholar
[27] Guo C S, Xie Y Y, Sha B 2014 Opt. Lett. 39 2338
Google Scholar
[28] Jacquot M, Sandoz P, Tribillon G 2001 Opt. Commun. 190 87
Google Scholar
[29] Cuche E, Marquet P, Depeursinge C 1999 Appl. Opt. 38 6994
Google Scholar
[30] Guo C S, Zhang L, Rong Z Y, Wang H T 2003 Opt. Eng. 42 2768
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7167
- PDF Downloads: 55
- Cited By: 0
