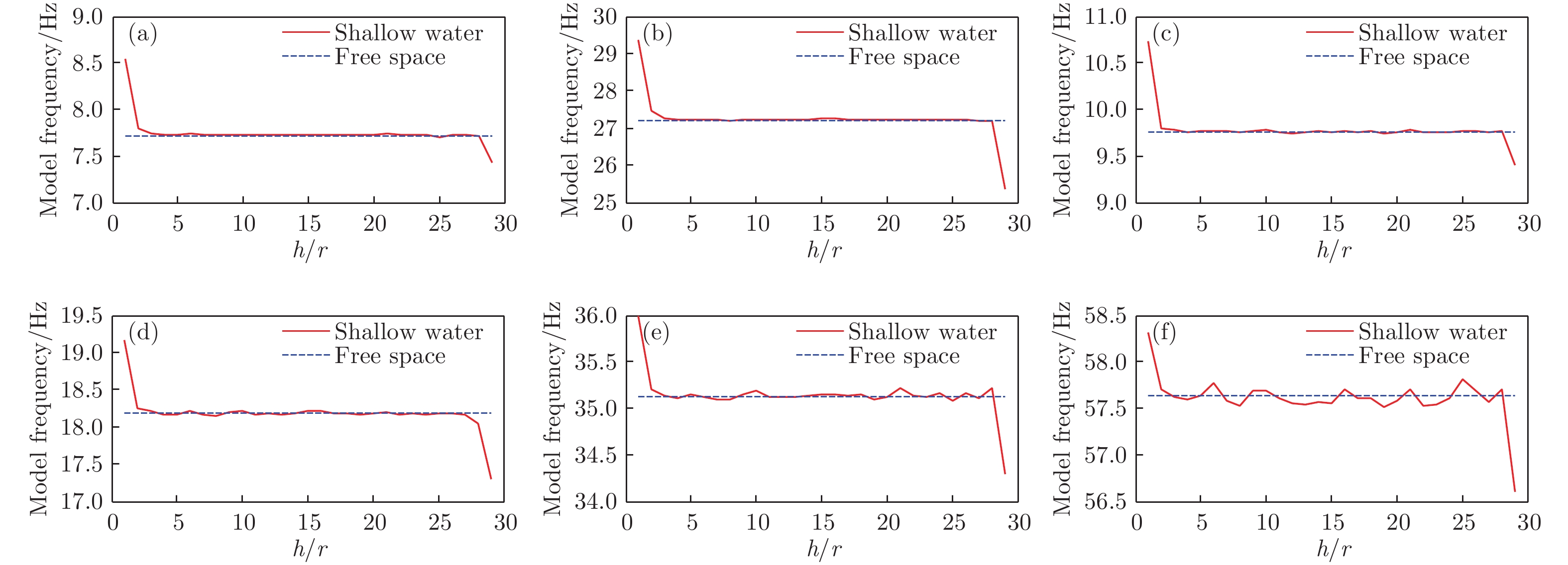
-
It can be a difficult problem to precisely predict the acoustic field radiated from a finite elastic structure in shallow water channel because of its strong coupling with up-down boundaries and the fluid medium, whose acoustic field cannot be calculated directly by existing methods, such as Ray theory, normal mode theory and other different methods, which are adaptable to sound fields from idealized point sources in waveguide. So, there is no reliable research method of predicting the acoustic radiation of elastic structure in shallow water at present. Based on the finite element method (FEM) coupled with the parabolic equation (PE), the theoretical model for structure acoustic radiation in shallow water at low frequency is established in this paper. This model mainly consists of three sections. First, obtaining the near-field vibro-acoustic characteristics of the elastic structure in shallow water by the multi-physics coupling model established by FEM, whose FEM model includes the up-down boundaries and the completely absorbent sound boundaries in the horizontal direction. Second, getting the acoustic information in the depth, which is set as the acoustic input condition i.e. starting field for the PE. Third, the acoustic information in the far-field quickly calculated by the PE and the finite difference method (FDM). The accuracy, efficiency and fast convergence of FEM-PE method are validated by numerical simulation and theoretical analysis through using a monopole source and structural source in the Pekeris waveguide, respectively. The vibro-acoustic characteristics of elastic cylinder influenced by upper and lower fluid boundaries of the Pekeris waveguide are calculated and analyzed. The cylindrical shell material is steel, and it is 1 m in radius and 10 m in length. The shallow water channel is a Pekeris waveguide with 30 m in depth, at the upper boundary, i.e., the free surface, the lower boundary is the semi-infinite liquid boundary. The analyzed frequencies range from 50 Hz to 200 Hz. The study shows that when the cylindrical shell approaches to the sea surface or bottom, the coupled frequency is higher or lower respectively than that of the shell immersed in the free field. When the diving depth reaches a certain distance range, the coupled frequency tends to be the same as that in free field. The acoustic field radiated from an elastic shell in Pekeris waveguide is similar to that from a point source at low frequency, but there exists a significant difference in high frequency between them, so the structural source can be equivalent to a point source conditionally. The sound radiation attenuation of the structure happens in sequence according to the near-field acoustic shadow zone, the spherical wave attenuation zone, the region between spherical wave and the cylindrical wave attenuation zone, and the cylindrical wave attenuation zone.
-
Keywords:
- shallow water /
- finite cylindrical shell /
- finite element-parabolic equation method /
- vibro-acoustic characteristics
[1] Junger M C, Feit D 1972 Sound, Structures, and Their Interaction (2th Ed.) (Massachusetts: MIT Press) pp279−309
[2] Sandberg G, Ohayon R 2009 Computational Aspects of Structural Acoustics and Vibration (New York: Springer Press) pp23−103
[3] Skelton E A, James J H 1997 Theoretical Acoustics of Underwater Structures (London: Imperial College Press) pp241−278
[4] Ho J 1994 J. Acoust Soc. Am. 96 525
Google Scholar
[5] Amabili M, Dalpiaz G 1995 J. Vib. Acoust. 117 187
Google Scholar
[6] 潘汉军, 李加庆, 陈进, 张桂才, 刘先锋 2006 中国机械工程 177 33
Google Scholar
Pan H J, Li J Q, Chen J, Zhang G C, Liu X F 2006 China Mech. Eng. 177 33
Google Scholar
[7] 叶文兵, 李天匀, 朱翔, 陈忱 2013 船舶力学 3 313
Ye W B, Li T Y, Zhu X, Chen C 2013 J. Shi. Mech. 3 313
[8] Skidan O, Klosner J M, Baron M L 1974 J. Acoust. Soc. Am. 56 427
Google Scholar
[9] Li W L, Wu T W, Seybert A F 1994 J. Sound Vib. 171 173
Google Scholar
[10] 郭文杰, 李天匀, 朱翔, 屈凯旸 2018 67 084302
Google Scholar
Guo W J, Li T Y, Qu K Y 2018 Acta Phys. Sin. 67 084302
Google Scholar
[11] Brunner D, Of G, Junge M 2010 Int. J. Num. Methods Eng. 81 28
[12] Soni S, Jain N K, Joshi P V 2018 J. Sound Vib. 412 28
Google Scholar
[13] Ergin A, Price W G, Randall R, Temarel P 1992 J. Ship Res. 36 154
[14] 白振国, 吴文伟, 左成魁, 张峰, 熊晨熙 2014 船舶力学 Z1 178
Google Scholar
Bai Z G, Wu W W, Zuo C K, Zhang F, Xiong C X 2014 J. Shi. Mech. Z1 178
Google Scholar
[15] Wang P, Li T Y, Zhu X 2017 Ocean Eng. 142 280
Google Scholar
[16] Sarkissian A 1994 J. Acoust. Soc. Am. 95 2340
Google Scholar
[17] 商德江, 钱治文, 何元安, 肖妍 2018 67 084301
Shang D J, Qian Z W, He Y A, Xiao Y 2018 Acta Phys. Sin. 67 084301
[18] Zou M S, Wu Y S, Liu Y M, Lin C G 2013 J. Hydrodyn. 25 929
Google Scholar
[19] Jiang L W, Zou M S, Huang H, Feng X L 2018 JASA Express Lett. 43 EL430
[20] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (2th Ed.) (New York: Springer) pp457−527
[21] 秦继兴, Boris K, 彭朝晖, 李整林, 张仁和, 骆文于 2016 65 034301
Google Scholar
Qin J X, Boris K, Peng Z H, Li Z L, Zhang R H, Luo W Y 2016 Acta Phys. Sin. 65 034301
Google Scholar
[22] Luo W Y, Yu X L, Yang X F, Zhang Z Z, Zhang R H 2016 Chin. Phys. B 25 124309
[23] Xu C X, Tang J, Piao S C, Liu J Q, Zhang S Z 2016 Chin. Phys. B 12 124315
[24] Collins M D, Evans R B 1992 J. Acoust. Soc. Am. 91 1357
Google Scholar
[25] Collins M D 1993 J. Acoust. Soc. Am. 93 1815
Google Scholar
[26] Collins M D, Siegmann W L 2015 J. Acoust. Soc. Am. 137 492
Google Scholar
[27] Yevick D, Thomson D J 2000 J. Acoust. Soc. Am. 107 1226
Google Scholar
[28] Tang J, Piao S C, Zhang H G 2017 Chin. Phys. B 26 269
[29] Isakson M J, Goldsberry B, Chotiros N P 2014 J. Acoust. Soc. Am. 136 EL206
Google Scholar
[30] Wu H T, Chen P T 2017 J. Marine Sci. Technol. 25 96
[31] Marburg S, Nolte B 2008 Computational Acoustics of Noise Propagation in Fluids: Finite and Boundary Element Methods (New York: Acoustics Springer) pp166–178
[32] Pappert F D 1977 The Parabolic Approximation Method// Wave Propagation and Underwater Acoustics (New York: Springer) pp224–287
[33] Lee D, Mcdaniel S T 1987 Ocean Acoustic Propagation by Finite Difference Methods (New York: Pergamon) pp313−316
[34] Collins M D 1989 J. Acoust. Soc. Am. 86 1459
Google Scholar
[35] Brekhovskikh L M, Lysanov Y P 2004 Fundamentals of Ocean Acoustics (3th Ed.) (New York: Springer) pp102–116
[36] 何祚镛, 赵玉芳 1981 声学理论基础(北京: 国防工业出版社) 第194−307页
He Z Y, Zhao Y F 1981 Theories of Acoustics (Beijing: National Defense Industry Press) pp194−307 （in Chinese）
-
图 1 浅海波导下结构声辐射FEM-PE计算原理图
Figure 1. Principle of FEM-PE in shallow water.
图 2 Crank-Nicolson有限差分法示意图
Figure 2. Schematic diagram of IFDM used Crank-Nicolson.
图 3 浅海波导下点源声传播模型
Figure 3. Acoustic propagation model of point source in shallow water.
图 4 点源的FEM-PE理论验证 (a) f = 30 Hz; (b) f = 300 Hz
Figure 4. Verification of point source used FEM-PE: (a) f = 30 Hz; (b) f = 300 Hz.
图 5 浅海下弹性球壳声辐射有限元模型示意图
Figure 5. FEM model diagram of elastic spherical shell in shallow water.
图 6 弹性球壳的FEM-PE理论验证 (a) f = 30 Hz; (b) f = 300 Hz
Figure 6. Verification of elastic sphere used FEM-PE: (a) f = 30 Hz; (b) f = 300 Hz.
图 7 60 Hz频率下FEM-PE与CWSM计算结果对比
Figure 7. Contrast between method of FEM-PE and CWSM at 60 Hz.
图 8 浅海波导下圆柱壳声辐射FEM-PE预报模型
Figure 8. Model of cylindrical sound radiation used FEM-PE in shallow water.
图 9 耦合模态随潜深的变化曲线 (a) (4, 1); (b) (4, 2); (c) (6, 1); (d) (6, 2); (e) (6, 3); (f) (6, 4)
Figure 9. Curves of coupled modal frequency changed with diving depth: (a) Modal (4, 1); (b) modal (4, 2); (c) modal (6, 1); (d) modal (6, 2); (e) modal (6, 3); (f) modal (6, 4).
图 10 不同频率下结构声场传播伪彩图 (a) f = 50 Hz; (b) f = 100 Hz; (c) f=150 Hz; (d) f = 200 Hz
Figure 10. Colour maps of structural sound propagation at different frequencies: (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz.
图 11 不同频率下结构辐射声场与点源声场对比 (a) f = 50 Hz; (b) f = 100 Hz; (c)f = 150 Hz; (d) f = 200 Hz
Figure 11. Acoustic propagation contrast between structure and point souce at different frequencies: (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz.
图 12 不同频率下结构辐射场传播特性分析 (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz
Figure 12. Analysis of structural sound propagation at different frequencies: (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz.
表 1 方法收敛性分析
Table 1. Convergence analysis of the method.
FEM $\scriptstyle {d_{\rm FEM}}$ $\scriptstyle \lambda $ $\frac{\lambda }{2}$ $\frac{\lambda }{4}$ $\frac{\lambda }{6}$ $\frac{\lambda }{8}$ $\frac{\lambda }{{10}}$ $\frac{\lambda }{6}$ PE $\scriptstyle {d_z}$ $\frac{\lambda }{8}$ $\scriptstyle \lambda $ $\frac{\lambda }{2}$ $\frac{\lambda }{4}$ $\frac{\lambda }{8}$ $\frac{\lambda }{{16}}$ $\scriptstyle {d_r}=2{d_z}$ $\frac{\lambda }{4}$ $\scriptstyle 2\lambda $ $\scriptstyle \lambda $ $\frac{\lambda }{2}$ $\frac{\lambda }{4}$ $\frac{\lambda }{8}$ $\scriptstyle \varpi $/％ 11.6 6.8 4.2 3.3 3.4 3.5 13.8 11.2 7.8 3.3 3.5 DOF/$\scriptstyle \times {10^4}$ 2.2 3.4 7.2 13.1 20.9 40.9 11.5 11.6 11.9 13.1 17. 7 RAM/GB 1.9 2.0 1.9 2.0 2.2 2.5 2.0 2.0 2.0 2.0 2.1 t/s 2.3 4.5 7.5 12.4 17.3 21.9 11.5 11.6 11. 7 12.4 14.1 
DownLoad: CSV
表 2 运行时间对比测试 (单位: min)
Table 2. The contrast test of runtime between FEM-PE and CWSM (unit: min).
l/km $\scriptstyle \lambda-5$ $\scriptstyle \lambda-1$ $\scriptstyle \lambda-10$ $\scriptstyle \lambda-50$ $\scriptstyle \lambda-100$ f/Hz 30 60 90 100 60 t CWSM 24.62 40.47 62.00 68.78 27.97 98.98 189.57 276.68 FEM-PE 2.20 4.18 7.21 9.45 2.17 5.98 11.60 18.76 $\textstyle {\eta _{\rm CWSM/FEM {\text{-}} PE}}$ 11 : 1 10 : 1 9 : 1 8 : 1 14 : 1 17 : 1 16 : 1 14 : 1 注: $\textstyle {\eta _{\rm CWSM/FEM{\text{-}}PE}}$为两种方法时间比值, FEM-PE网格为$\scriptstyle {d_{\rm FEM}}=\lambda /6$, $\scriptstyle {d_z}=\lambda /8$及$\scriptstyle {d_r}=\lambda /4$.
DownLoad: CSV
表 3 不同流体环境下圆柱壳耦合模态频率(单位: Hz)
Table 3. Comparison of coupled modal frequency in different fluid environments (unit: Hz).
Environment 
(4, 1)
(4, 2)
(6, 1)
(6, 2)
(6, 3)
(6, 4)Free field 7.72 27.18 9.75 18. 19 35.12 57.63 Half-space 7.83 27.53 9.87 18.41 35.62 58.18 Pekeris 7.80 27.42 9.80 18.26 35.26 57.71
DownLoad: CSV
表 4 Pekeris波导中各阶简正波频率
Table 4. Normal mode frequencies in Pekeris waveguide.
n 1 2 3 4 5 6 f/Hz 35.52 106.56 177.60 248.65 319.69 390.73
DownLoad: CSV
-
[1] Junger M C, Feit D 1972 Sound, Structures, and Their Interaction (2th Ed.) (Massachusetts: MIT Press) pp279−309
[2] Sandberg G, Ohayon R 2009 Computational Aspects of Structural Acoustics and Vibration (New York: Springer Press) pp23−103
[3] Skelton E A, James J H 1997 Theoretical Acoustics of Underwater Structures (London: Imperial College Press) pp241−278
[4] Ho J 1994 J. Acoust Soc. Am. 96 525
Google Scholar
[5] Amabili M, Dalpiaz G 1995 J. Vib. Acoust. 117 187
Google Scholar
[6] 潘汉军, 李加庆, 陈进, 张桂才, 刘先锋 2006 中国机械工程 177 33
Google Scholar
Pan H J, Li J Q, Chen J, Zhang G C, Liu X F 2006 China Mech. Eng. 177 33
Google Scholar
[7] 叶文兵, 李天匀, 朱翔, 陈忱 2013 船舶力学 3 313
Ye W B, Li T Y, Zhu X, Chen C 2013 J. Shi. Mech. 3 313
[8] Skidan O, Klosner J M, Baron M L 1974 J. Acoust. Soc. Am. 56 427
Google Scholar
[9] Li W L, Wu T W, Seybert A F 1994 J. Sound Vib. 171 173
Google Scholar
[10] 郭文杰, 李天匀, 朱翔, 屈凯旸 2018 67 084302
Google Scholar
Guo W J, Li T Y, Qu K Y 2018 Acta Phys. Sin. 67 084302
Google Scholar
[11] Brunner D, Of G, Junge M 2010 Int. J. Num. Methods Eng. 81 28
[12] Soni S, Jain N K, Joshi P V 2018 J. Sound Vib. 412 28
Google Scholar
[13] Ergin A, Price W G, Randall R, Temarel P 1992 J. Ship Res. 36 154
[14] 白振国, 吴文伟, 左成魁, 张峰, 熊晨熙 2014 船舶力学 Z1 178
Google Scholar
Bai Z G, Wu W W, Zuo C K, Zhang F, Xiong C X 2014 J. Shi. Mech. Z1 178
Google Scholar
[15] Wang P, Li T Y, Zhu X 2017 Ocean Eng. 142 280
Google Scholar
[16] Sarkissian A 1994 J. Acoust. Soc. Am. 95 2340
Google Scholar
[17] 商德江, 钱治文, 何元安, 肖妍 2018 67 084301
Shang D J, Qian Z W, He Y A, Xiao Y 2018 Acta Phys. Sin. 67 084301
[18] Zou M S, Wu Y S, Liu Y M, Lin C G 2013 J. Hydrodyn. 25 929
Google Scholar
[19] Jiang L W, Zou M S, Huang H, Feng X L 2018 JASA Express Lett. 43 EL430
[20] Jensen F B, Kuperman W A, Porter M B, Schmidt H 2011 Computational Ocean Acoustics (2th Ed.) (New York: Springer) pp457−527
[21] 秦继兴, Boris K, 彭朝晖, 李整林, 张仁和, 骆文于 2016 65 034301
Google Scholar
Qin J X, Boris K, Peng Z H, Li Z L, Zhang R H, Luo W Y 2016 Acta Phys. Sin. 65 034301
Google Scholar
[22] Luo W Y, Yu X L, Yang X F, Zhang Z Z, Zhang R H 2016 Chin. Phys. B 25 124309
[23] Xu C X, Tang J, Piao S C, Liu J Q, Zhang S Z 2016 Chin. Phys. B 12 124315
[24] Collins M D, Evans R B 1992 J. Acoust. Soc. Am. 91 1357
Google Scholar
[25] Collins M D 1993 J. Acoust. Soc. Am. 93 1815
Google Scholar
[26] Collins M D, Siegmann W L 2015 J. Acoust. Soc. Am. 137 492
Google Scholar
[27] Yevick D, Thomson D J 2000 J. Acoust. Soc. Am. 107 1226
Google Scholar
[28] Tang J, Piao S C, Zhang H G 2017 Chin. Phys. B 26 269
[29] Isakson M J, Goldsberry B, Chotiros N P 2014 J. Acoust. Soc. Am. 136 EL206
Google Scholar
[30] Wu H T, Chen P T 2017 J. Marine Sci. Technol. 25 96
[31] Marburg S, Nolte B 2008 Computational Acoustics of Noise Propagation in Fluids: Finite and Boundary Element Methods (New York: Acoustics Springer) pp166–178
[32] Pappert F D 1977 The Parabolic Approximation Method// Wave Propagation and Underwater Acoustics (New York: Springer) pp224–287
[33] Lee D, Mcdaniel S T 1987 Ocean Acoustic Propagation by Finite Difference Methods (New York: Pergamon) pp313−316
[34] Collins M D 1989 J. Acoust. Soc. Am. 86 1459
Google Scholar
[35] Brekhovskikh L M, Lysanov Y P 2004 Fundamentals of Ocean Acoustics (3th Ed.) (New York: Springer) pp102–116
[36] 何祚镛, 赵玉芳 1981 声学理论基础(北京: 国防工业出版社) 第194−307页
He Z Y, Zhao Y F 1981 Theories of Acoustics (Beijing: National Defense Industry Press) pp194−307 （in Chinese）
DownLoad:
Catalog
Metrics
- Abstract views: 9259
- PDF Downloads: 80
- Cited By: 0
