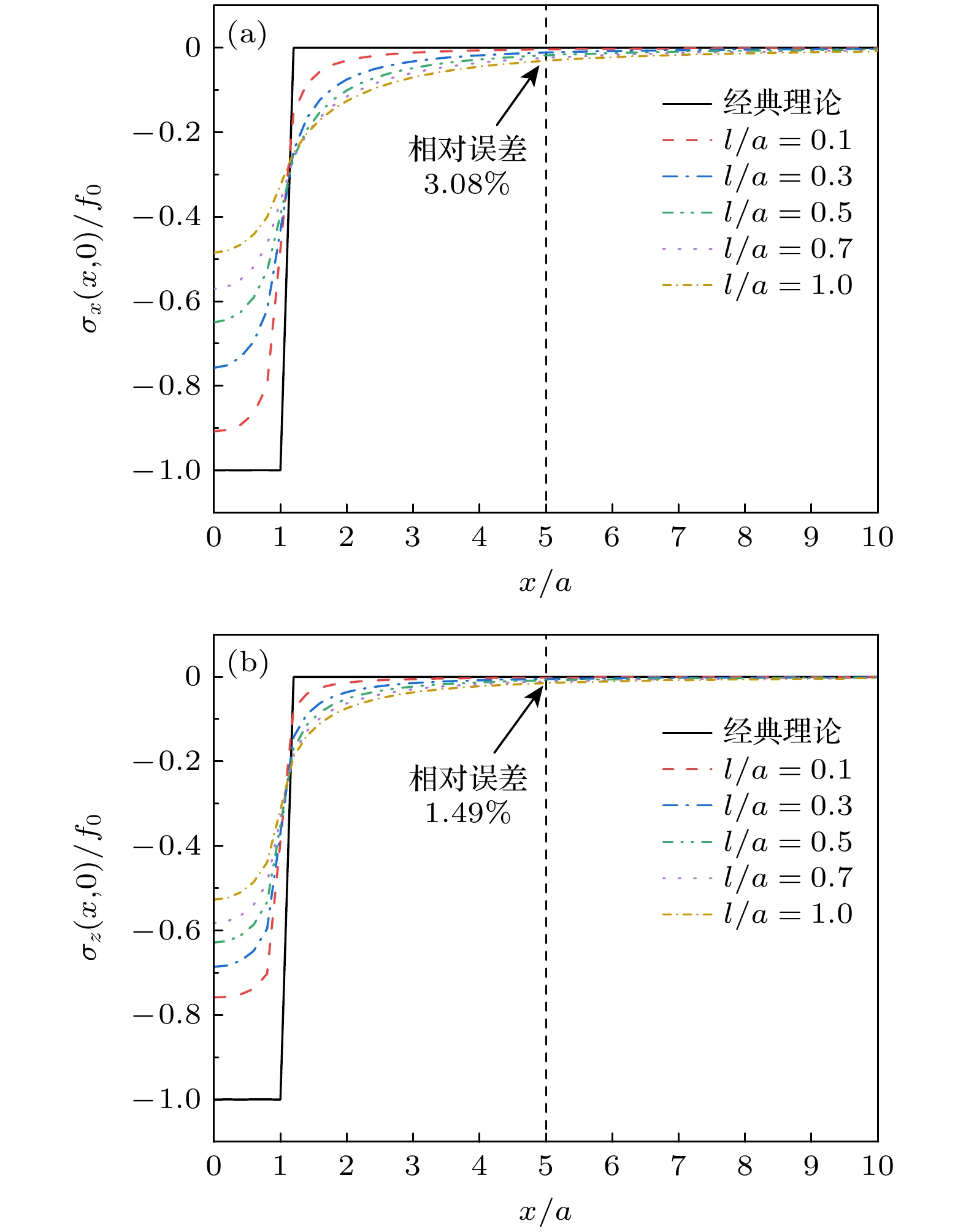
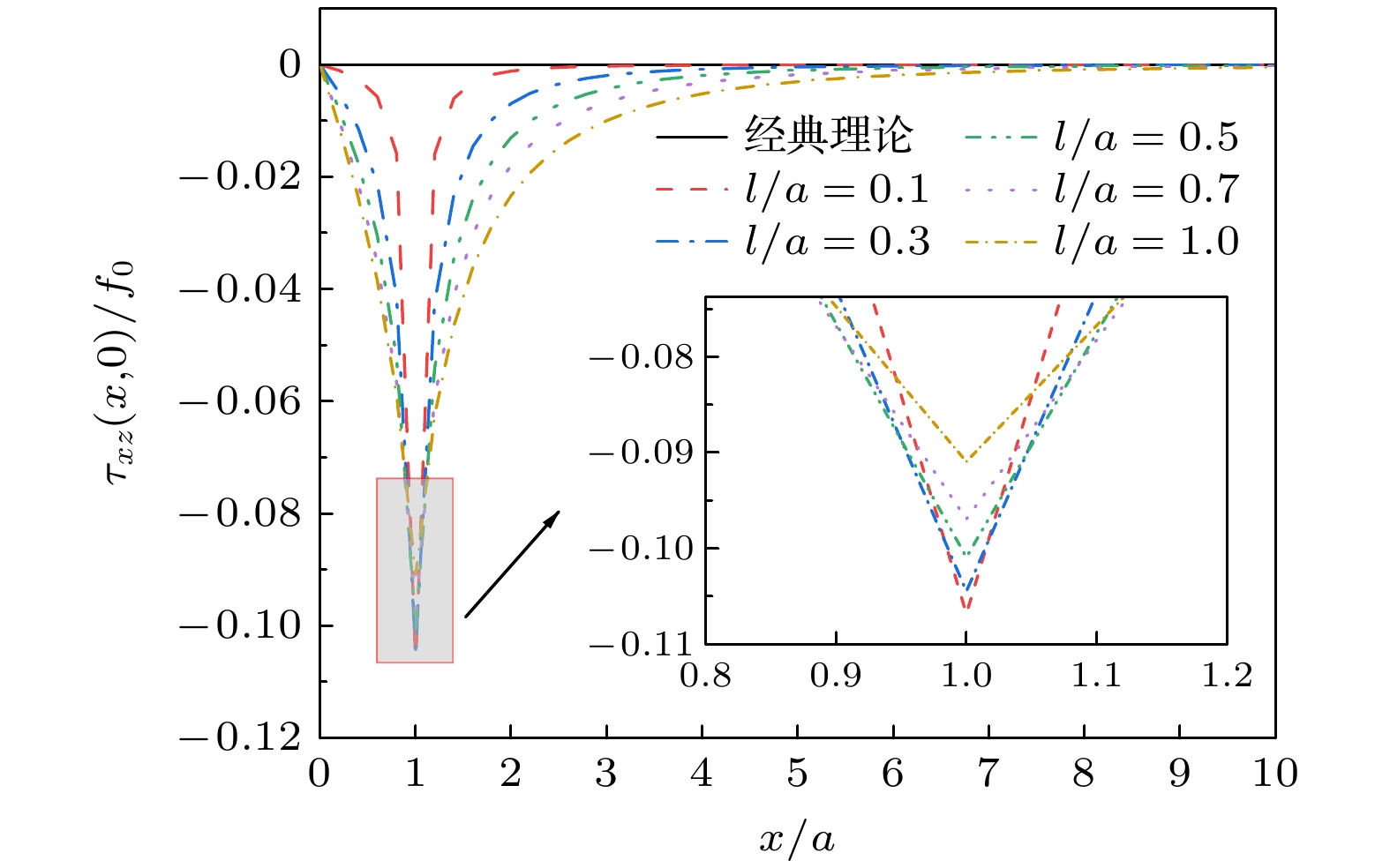
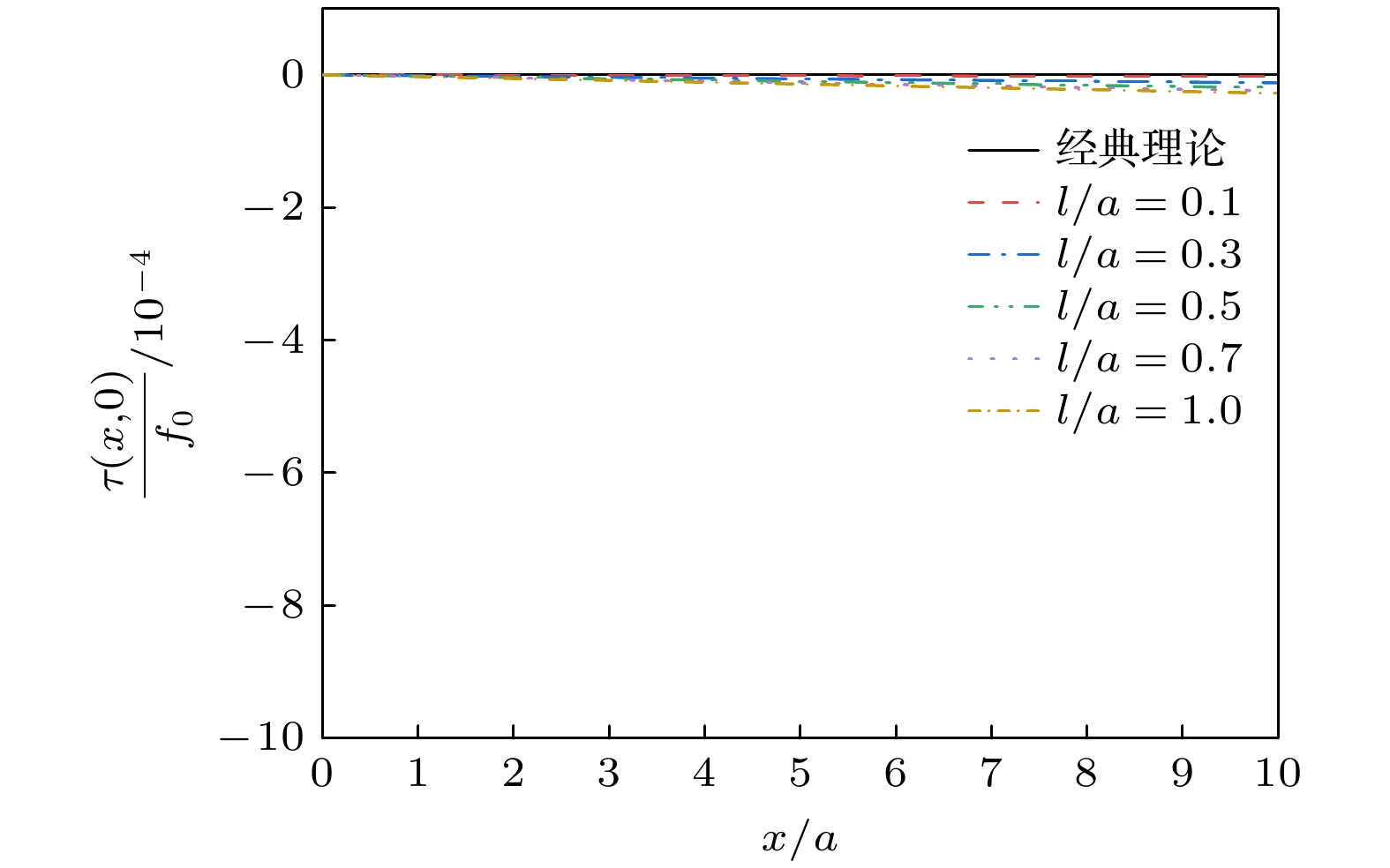
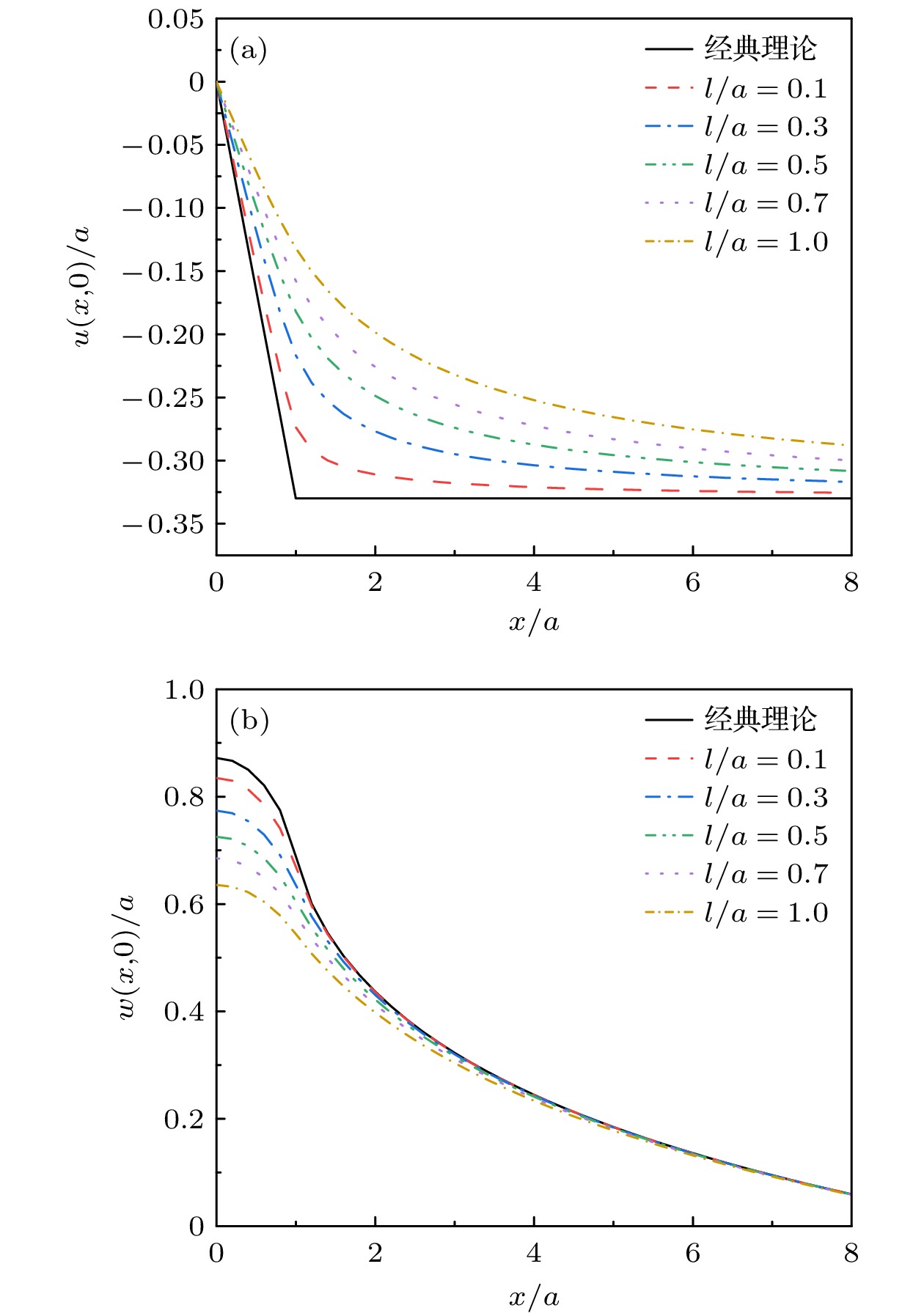
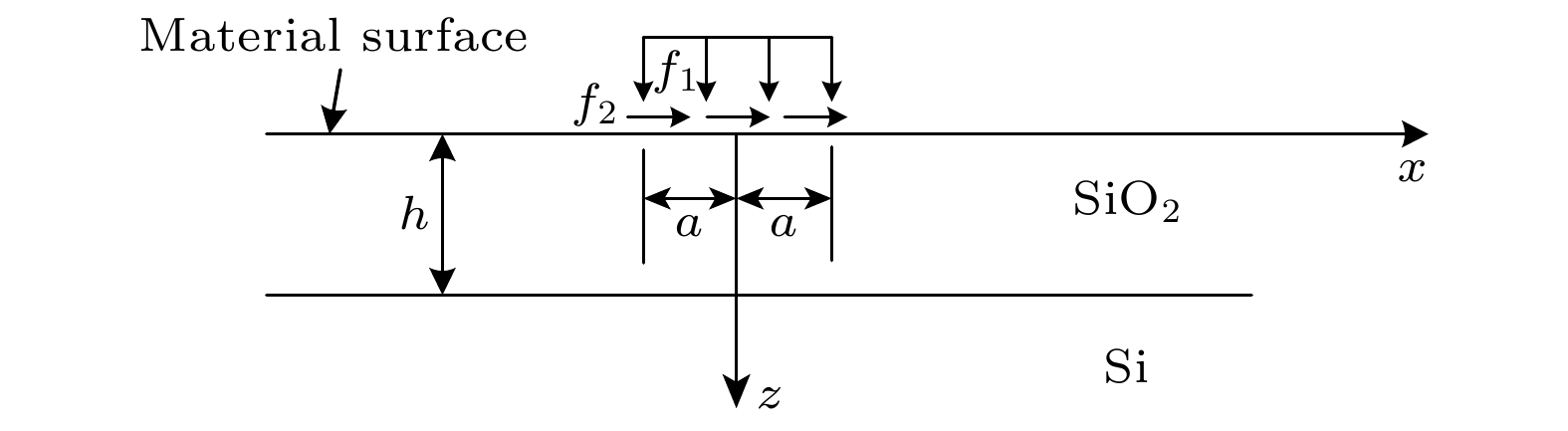
-
随着微纳声学器件的快速发展, 其核心声学结构已进入纳米尺度范畴, 表面效应对薄膜材料性能的影响日益凸显, 经典弹性理论面临挑战. 本文基于表面弹性理论, 引入表面能密度研究纳米尺度下的表面效应, 采用傅里叶积分变换法推导出纳米尺度SiO2/Si异质结构薄膜表面牵引力下应力场与位移场的解析表达式. 结果显示, 若以表面应力分布与经典理论相差3%作为判断标准, 在激励区域宽度2a的5倍范围内, 材料的微观特性彰显主导地位. 随着激励区域不断减小, 在激励区域内及边界附近表面应力分布较经典理论更加集中, 剪切应力于边界处有极大值, 材料表面刚度与抗变形能力增加, 横向与纵向位移较经典理论减小. 纳米尺度异质结构存在显著表面效应, 导致应力和位移分布明显偏离弹性理论, 经典弹性假设在相应纳米尺度范围不再适用. 以上结果表明, 在纳米尺度固体表面中, 超高频纳米波长声波传播将明显受到尺度效应影响, 经典弹性波理论在纳米尺度存在失效现象, 这对纳米声学理论研究具有参考价值.The rapid advancement of micro-nano acoustic devices has led their core acoustic structures to shrink to the nanoscale level. The influence of surface effects on the mechanical properties of thin-film materials on a nanoscale becomes increasingly prominent, and the classical elasticity theory struggles to accurately describe their mechanical behavior on this scale. In this paper, a mechanical model of nano-SiO2/Si heterostructured thin films that considers surface effects is developed using surface elasticity theory. This model incorporates the key parameter of surface energy density. In this paper, a mechanical model of heterostructured nano-SiO2/Si films is developed using the surface elasticity theory, incorporating surface effects through the introduction of surface energy density as a key parameter. Using the Fourier integral transform method, analytical expressions for stress and displacement fields under surface traction are systematically derived, revealing the influence of surface effects on the mechanical behavior of materials on a nanoscale by comparing the analytical solution with that from the classical theory. The results show that when the surface stress distribution deviates by 3% from that predicted by the classical theory, the microscopic properties of the material become significant, and the surface effect cannot be ignored in a range of five times the width of the excitation region 2a. As the size of the excitation region decreases, the surface effect is significantly increases and the stress distribution within the excitation region and near the boundary becomes more concentrated than the counterparts in the classical theory. The shear stress is no longer zero, and an extreme value is observed at the boundary, which is significantly different from that predicted by the classical theory of elasticity. The transverse and longitudinal displacements are reduced compared with those from the classical theory, and the surface stiffness and deformation resistance of the material are greatly enhanced. Significant surface effects occur on nano-heterostructure thin films, leading to large deviations in stress and displacement distributions from the results of elasticity theory. Therefore, the classical elasticity assumptions are no longer applicable in the corresponding nanoscale range. The results demonstrate that the propagation of ultrahigh-frequency nano- length acoustic waves in nanoscale solid film surfaces is significantly affected by the scale effect. The failure of the classical elastic wave theory on a nanoscale is of great value for the study of nanoscale acoustic theory. Furthermore, these findings provide a theoretical basis for the subsequent development of more precise models of interfacial effects and a more detailed investigation of the influence of the film-substrate modulus ratio.
-
Keywords:
- surface elasticity theory /
- nanoscale /
- surface effects /
- failure phenomenon
[1] Hui X P 2024 Acta Mech. Solida Sin. 37 371
Google Scholar
[2] Farajpour A, Ghayesh H M, Farokhi H 2018 Int. J. Eng. Sci. 133 231
Google Scholar
[3] Peddieson J, Buchanan R G, McNitt P R 2003 Int. J. Eng. Sci. 41 305
Google Scholar
[4] Eringen A C 1999 Theory of Micropolar Elasticity (New York: Springer
[5] Toupin R A 1964 Arch. Ration. Mech. Anal. 17 85
Google Scholar
[6] Gibbs J W 1879 Trans. Conn. Acad. 2 300
Google Scholar
[7] Gurtin M E, Murdoch A I 1975 Arch. Ration. Mech. Anal. 59 389-390
Google Scholar
[8] Miller R E, Shenoy V B 2000 Nanotechnology 11 139
Google Scholar
[9] He J, Lilley C M 2008 Nano Lett. 8 1798
Google Scholar
[10] Tong L H, Lin F, Xiang Y, Shen H S, Lim C W 2021 Compos. Struct. 265 113708
Google Scholar
[11] Zhang S Y, Tang X Y, Ruan H H, Zhu L L 2019 Appl. Phys. A 125 1
Google Scholar
[12] Chen S H, Yao Y 2014 Appl. Mech. 81 121002
Google Scholar
[13] Zhang Y Y, Wang Y X, Zhang X, Shen H M, She G L 2021 Steel Compos. Struct. 38 293
Google Scholar
[14] Wang L Y, Wu H M, Ou Z Y 2024 Math. Mech. Solids 29 401
Google Scholar
[15] George V, Mohammadreza Y 2017 Crystals 7 321
Google Scholar
[16] Saffari S, Hashemian M, Toghraie D 2017 Physica B 520 97
Google Scholar
[17] Chen D Q, Sun D L, Li X F 2017 Compos. Struct. 173 116
Google Scholar
[18] 叶高杰, 殷澄, 黎思瑜, 俞强, 王贤平, 吴坚 2023 72 104201
Google Scholar
Ye G J, Yin C, Li S Y, Wang X P, Wu J 2023 Acta Phys. Sin. 72 104201
Google Scholar
[19] 尚帅朋, 陆勇俊, 王峰会 2022 71 033101
Google Scholar
Shang S P, Lu Y J, Wang F H 2022 Acta Phys. Sin. 71 033101
Google Scholar
[20] Tian X G, Tao L Q, Liu B, Zhou C J, Ren T L 2016 IEEE Electron Device Lett. 37 1063
Google Scholar
[21] Shen B, Huang Z W, Ji Z, Lin Q, Chen S L, Cui D J, Zhang Z N 2019 Surf. Coat. Technol. 380 125061
Google Scholar
[22] Selvadurai A P S 2000 Partial Differential Equations in Mechanics (Berlin: Springer
[23] Ouyang G, Wang C X, Yang G W 2009 Chem. Rev. 109 4221
Google Scholar
[24] Zhang C, Yao Y, Chen S H 2014 Comput. Mater. Sci. 82 372
Google Scholar
[25] Yao Y, Chen S H 2016 Acta Mech. 227 1799
Google Scholar
[26] Gao X, Hao F, Fang D N, Huang Z P 2013 Int. J. Solids Struct. 50 2620
Google Scholar
[27] Wang L Y 2020 Int. J. Mech. Mater. Des. 16 633
Google Scholar
-
图 1 材料表面承受激励的弹性半平面示意图
Fig. 1. Schematic diagram of the elastic half plane of a material surface subjected to excitation.
图 2 表面应力分布情况 (a) x方向应力分量$ {\sigma _x} $; (b) z方向应力分量$ {\sigma _z} $
Fig. 2. Surface stress distribution: (a) x-direction stress component; (b) z-direction stress component $ {\sigma _z} $.
图 3 表面剪切应力$ {\tau _{xz}} $的分布情况
Fig. 3. Distribution of surface shear stress $ {\tau _{xz}} $.
图 5 表面位移分布 (a) 横向位移u; (b) 纵向位移w
Fig. 5. Surface displacement distribution: (a) Transverse displacement u; (b) longitudinal displacement w
-
[1] Hui X P 2024 Acta Mech. Solida Sin. 37 371
Google Scholar
[2] Farajpour A, Ghayesh H M, Farokhi H 2018 Int. J. Eng. Sci. 133 231
Google Scholar
[3] Peddieson J, Buchanan R G, McNitt P R 2003 Int. J. Eng. Sci. 41 305
Google Scholar
[4] Eringen A C 1999 Theory of Micropolar Elasticity (New York: Springer
[5] Toupin R A 1964 Arch. Ration. Mech. Anal. 17 85
Google Scholar
[6] Gibbs J W 1879 Trans. Conn. Acad. 2 300
Google Scholar
[7] Gurtin M E, Murdoch A I 1975 Arch. Ration. Mech. Anal. 59 389-390
Google Scholar
[8] Miller R E, Shenoy V B 2000 Nanotechnology 11 139
Google Scholar
[9] He J, Lilley C M 2008 Nano Lett. 8 1798
Google Scholar
[10] Tong L H, Lin F, Xiang Y, Shen H S, Lim C W 2021 Compos. Struct. 265 113708
Google Scholar
[11] Zhang S Y, Tang X Y, Ruan H H, Zhu L L 2019 Appl. Phys. A 125 1
Google Scholar
[12] Chen S H, Yao Y 2014 Appl. Mech. 81 121002
Google Scholar
[13] Zhang Y Y, Wang Y X, Zhang X, Shen H M, She G L 2021 Steel Compos. Struct. 38 293
Google Scholar
[14] Wang L Y, Wu H M, Ou Z Y 2024 Math. Mech. Solids 29 401
Google Scholar
[15] George V, Mohammadreza Y 2017 Crystals 7 321
Google Scholar
[16] Saffari S, Hashemian M, Toghraie D 2017 Physica B 520 97
Google Scholar
[17] Chen D Q, Sun D L, Li X F 2017 Compos. Struct. 173 116
Google Scholar
[18] 叶高杰, 殷澄, 黎思瑜, 俞强, 王贤平, 吴坚 2023 72 104201
Google Scholar
Ye G J, Yin C, Li S Y, Wang X P, Wu J 2023 Acta Phys. Sin. 72 104201
Google Scholar
[19] 尚帅朋, 陆勇俊, 王峰会 2022 71 033101
Google Scholar
Shang S P, Lu Y J, Wang F H 2022 Acta Phys. Sin. 71 033101
Google Scholar
[20] Tian X G, Tao L Q, Liu B, Zhou C J, Ren T L 2016 IEEE Electron Device Lett. 37 1063
Google Scholar
[21] Shen B, Huang Z W, Ji Z, Lin Q, Chen S L, Cui D J, Zhang Z N 2019 Surf. Coat. Technol. 380 125061
Google Scholar
[22] Selvadurai A P S 2000 Partial Differential Equations in Mechanics (Berlin: Springer
[23] Ouyang G, Wang C X, Yang G W 2009 Chem. Rev. 109 4221
Google Scholar
[24] Zhang C, Yao Y, Chen S H 2014 Comput. Mater. Sci. 82 372
Google Scholar
[25] Yao Y, Chen S H 2016 Acta Mech. 227 1799
Google Scholar
[26] Gao X, Hao F, Fang D N, Huang Z P 2013 Int. J. Solids Struct. 50 2620
Google Scholar
[27] Wang L Y 2020 Int. J. Mech. Mater. Des. 16 633
Google Scholar
-
[1] 杨志平, 孔熙, 石发展, 杜江峰. 金刚石表面纳米尺度水分子的相变观测. , 2022, 71(6): 067601. doi: 10.7498/aps.71.20211348 [2] 陈小明, 李国荣. BaTiO3基无铅陶瓷大电致伸缩系数. , 2022, 71(16): 167701. doi: 10.7498/aps.71.20220451 [3] 尚帅朋, 陆勇俊, 王峰会. 表面效应对纳米线电极屈曲失稳的影响. , 2022, 71(3): 033101. doi: 10.7498/aps.71.20211864 [4] 张梦, 姚若河, 刘玉荣. 纳米尺度金属-氧化物半导体场效应晶体管沟道热噪声模型. , 2020, 69(5): 057101. doi: 10.7498/aps.69.20191512 [5] 梁晋洁, 高宁, 李玉红. 表面效应对铁 ${\left\langle 100 \right\rangle} $ 间隙型位错环的影响. , 2020, 69(3): 036101. doi: 10.7498/aps.69.20191379[6] 杨东升, 刘官厅. 磁电弹性材料中含有带四条纳米裂纹的正4n边形纳米孔的反平面断裂问题. , 2020, 69(24): 244601. doi: 10.7498/aps.69.20200850 [7] 张烨, 张冉, 常青, 李桦. 壁面效应对纳米尺度气体流动的影响规律研究. , 2019, 68(12): 124702. doi: 10.7498/aps.68.20190248 [8] 彭劼扬, 王家海, 沈斌, 李浩亮, 孙昊明. 纳米颗粒的表面效应和电极颗粒间挤压作用对锂离子电池电压迟滞的影响. , 2019, 68(9): 090202. doi: 10.7498/aps.68.20182302 [9] 董杨, 杜博, 张少春, 陈向东, 孙方稳. 基于金刚石体系中氮-空位色心的固态量子传感. , 2018, 67(16): 160301. doi: 10.7498/aps.67.20180788 [10] 张龙艳, 徐进良, 雷俊鹏. 纳米尺度下气泡核化生长的分子动力学研究. , 2018, 67(23): 234702. doi: 10.7498/aps.67.20180993 [11] 张鹏飞, 乔春红, 冯晓星, 黄童, 李南, 范承玉, 王英俭. Non-Kolmogorov湍流大气中小尺度热晕效应线性理论. , 2017, 66(24): 244210. doi: 10.7498/aps.66.244210 [12] 梁培, 刘阳, 王乐, 吴珂, 董前民, 李晓艳. 表面悬挂键导致硅纳米线掺杂失效机理的第一性原理研究. , 2012, 61(15): 153102. doi: 10.7498/aps.61.153102 [13] 唐冬和, 杜磊, 王婷岚, 陈华, 陈文豪. 纳米尺度MOSFET过剩噪声的定性分析. , 2011, 60(10): 107201. doi: 10.7498/aps.60.107201 [14] 张冬仙, 刘 超, 章海军. 微纳米尺度红外光热膨胀效应及新型光热驱动方法研究. , 2008, 57(5): 3107-3112. doi: 10.7498/aps.57.3107 [15] 罗文雄, 黄世华, 由芳田, 彭洪尚. YBO3:Eu3+纳米晶发光特性. , 2007, 56(3): 1765-1769. doi: 10.7498/aps.56.1765 [16] 田建辉, 韩 旭, 刘桂荣, 龙述尧, 秦金旗. SiC纳米杆的弛豫性能研究. , 2007, 56(2): 643-648. doi: 10.7498/aps.56.643 [17] 谢根全, 韩 旭, 龙述尧, 田建辉. 基于非局部弹性理论的单壁碳纳米管轴向受压屈曲研究. , 2005, 54(9): 4192-4197. doi: 10.7498/aps.54.4192 [18] 曾华荣, 余寒峰, 初瑞清, 李国荣, 殷庆瑞, 唐新桂. PZT铁电薄膜纳米尺度铁电畴的场致位移特性. , 2005, 54(3): 1437-1441. doi: 10.7498/aps.54.1437 [19] 于洪滨, 杨威生. 石墨上纳米尺度金岛的形成. , 1997, 46(3): 500-504. doi: 10.7498/aps.46.500 [20] 卢鹤绂. 关於流体的容变粘滞弹性理论及其在声吸收现象中的应用. , 1956, 12(1): 5-19. doi: 10.7498/aps.12.5
下载:
计量
- 文章访问数: 467
- PDF下载量: 5
- 被引次数: 0
