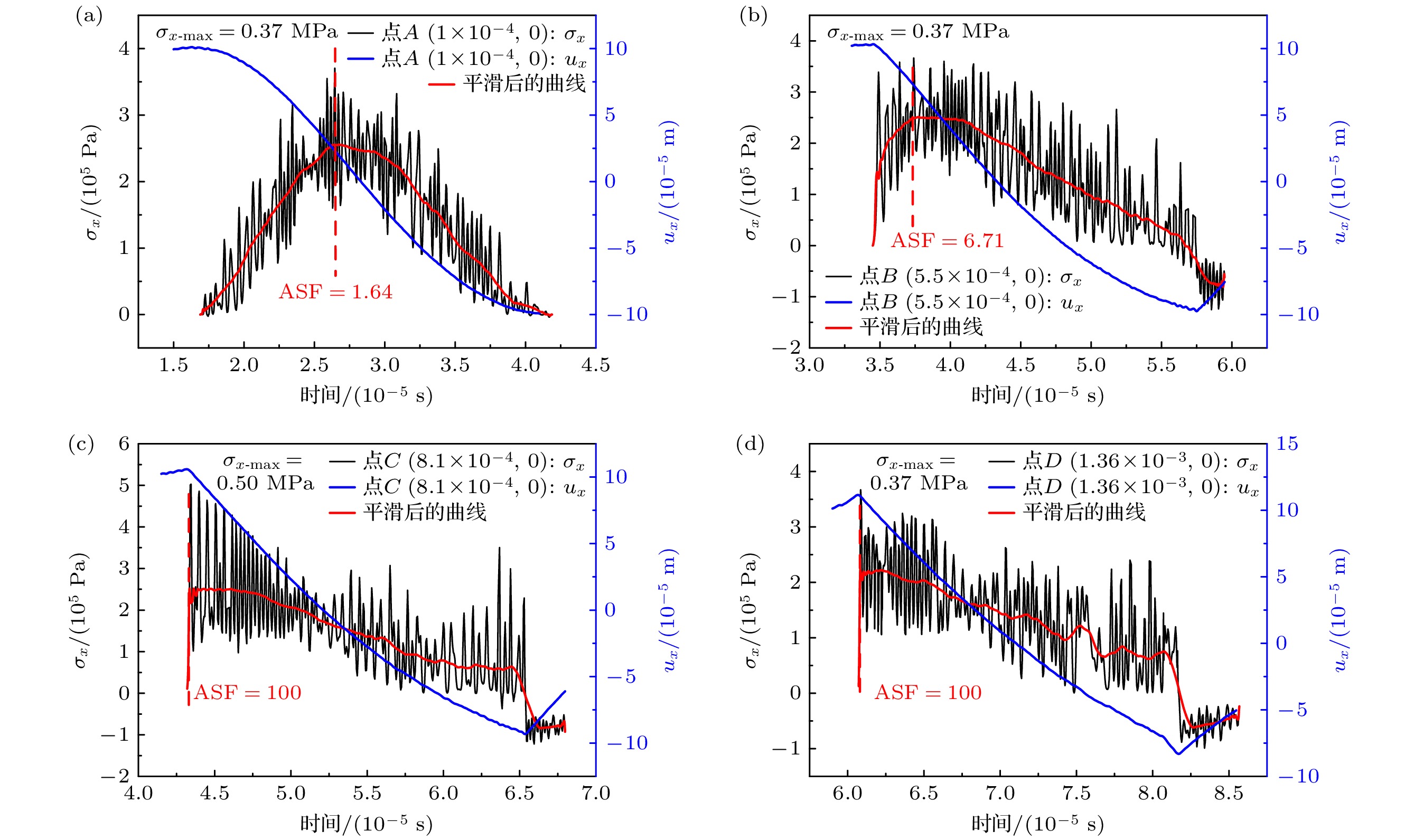
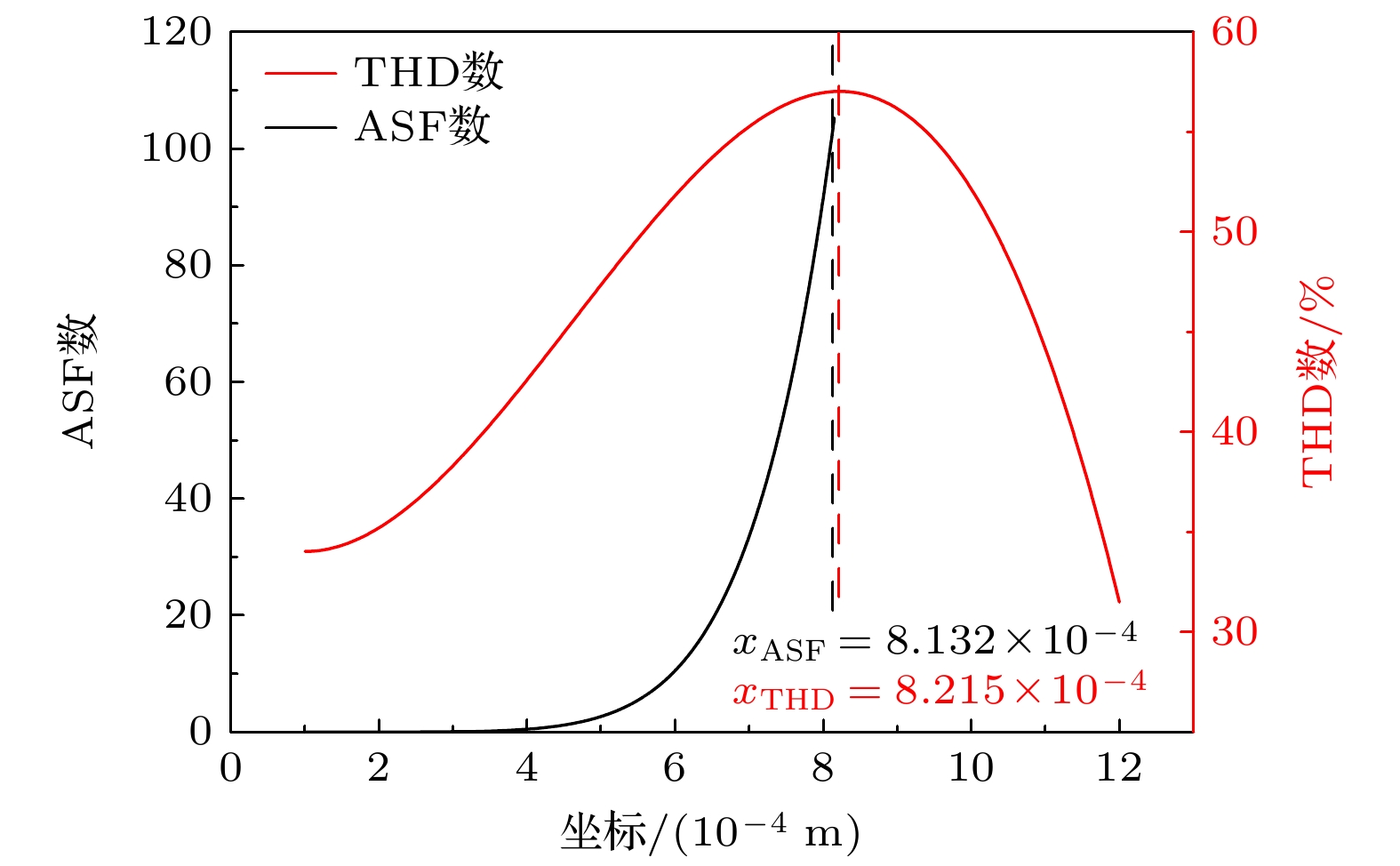
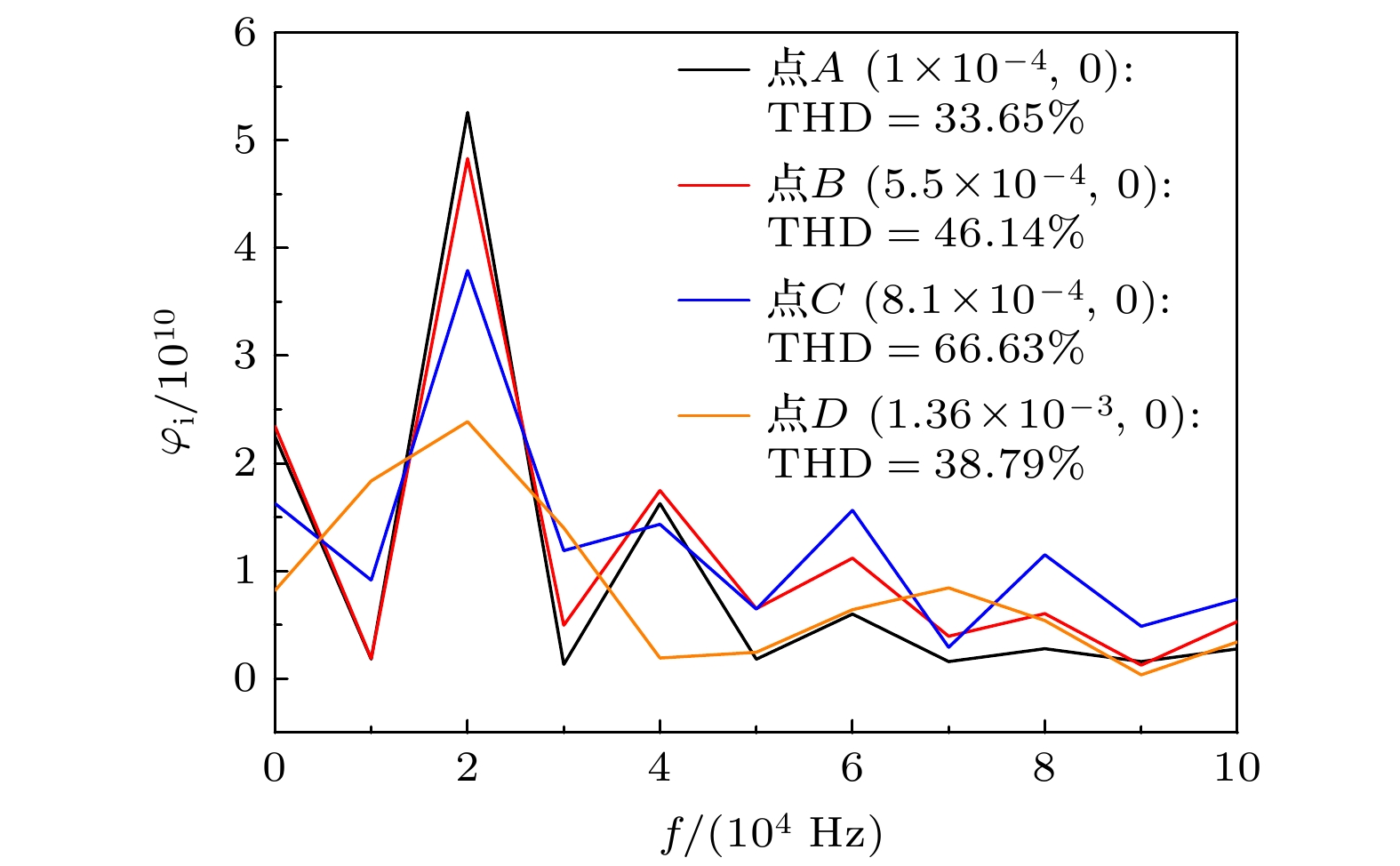
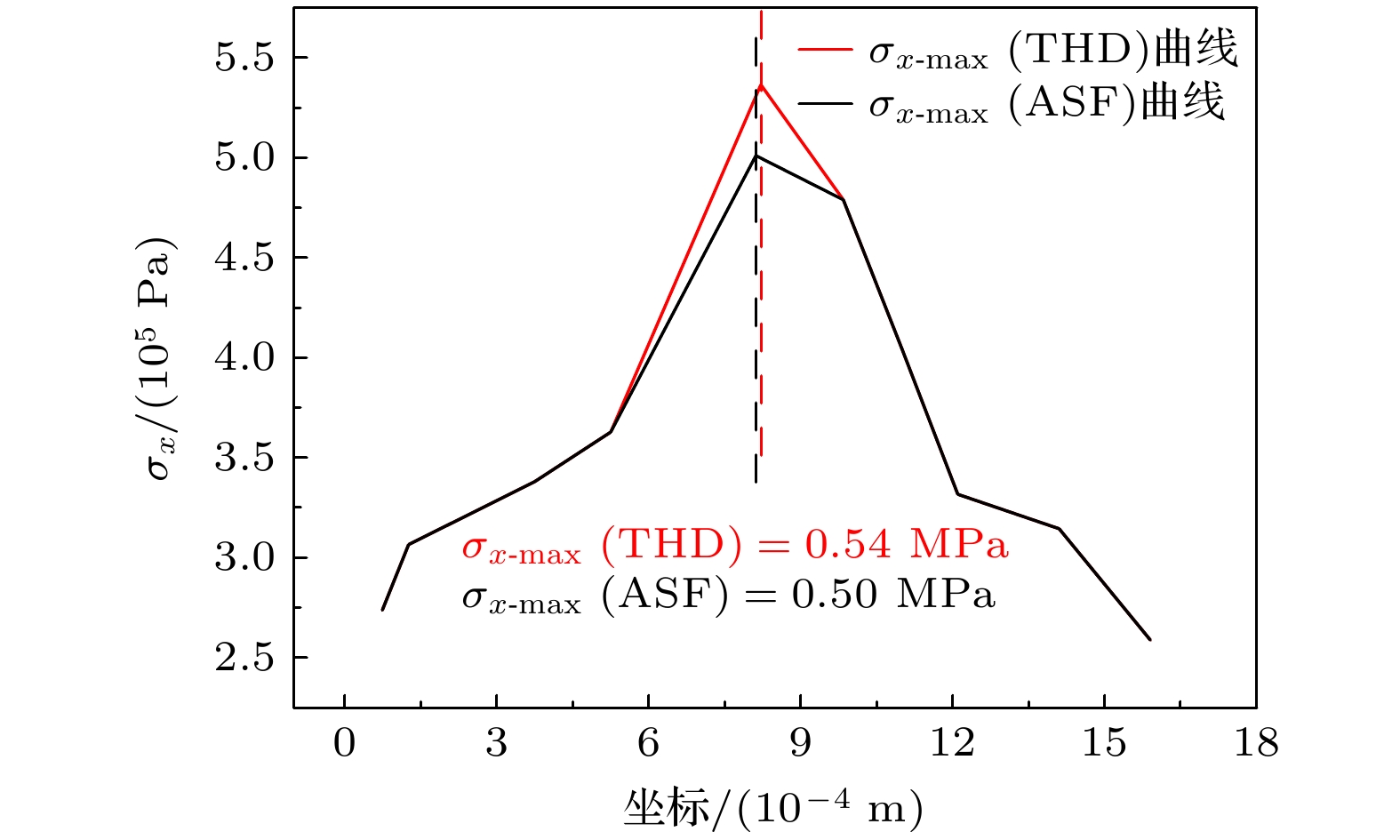
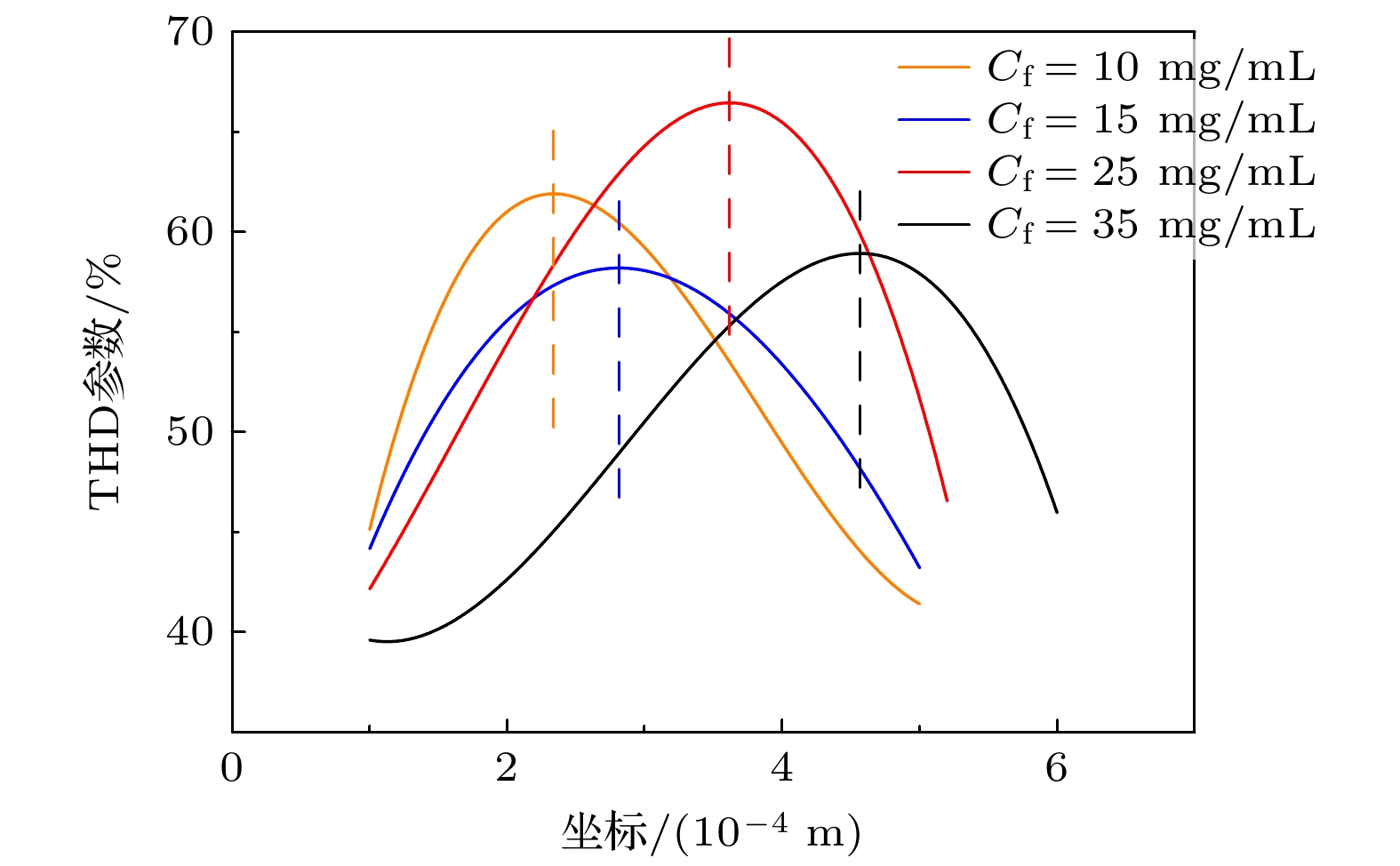
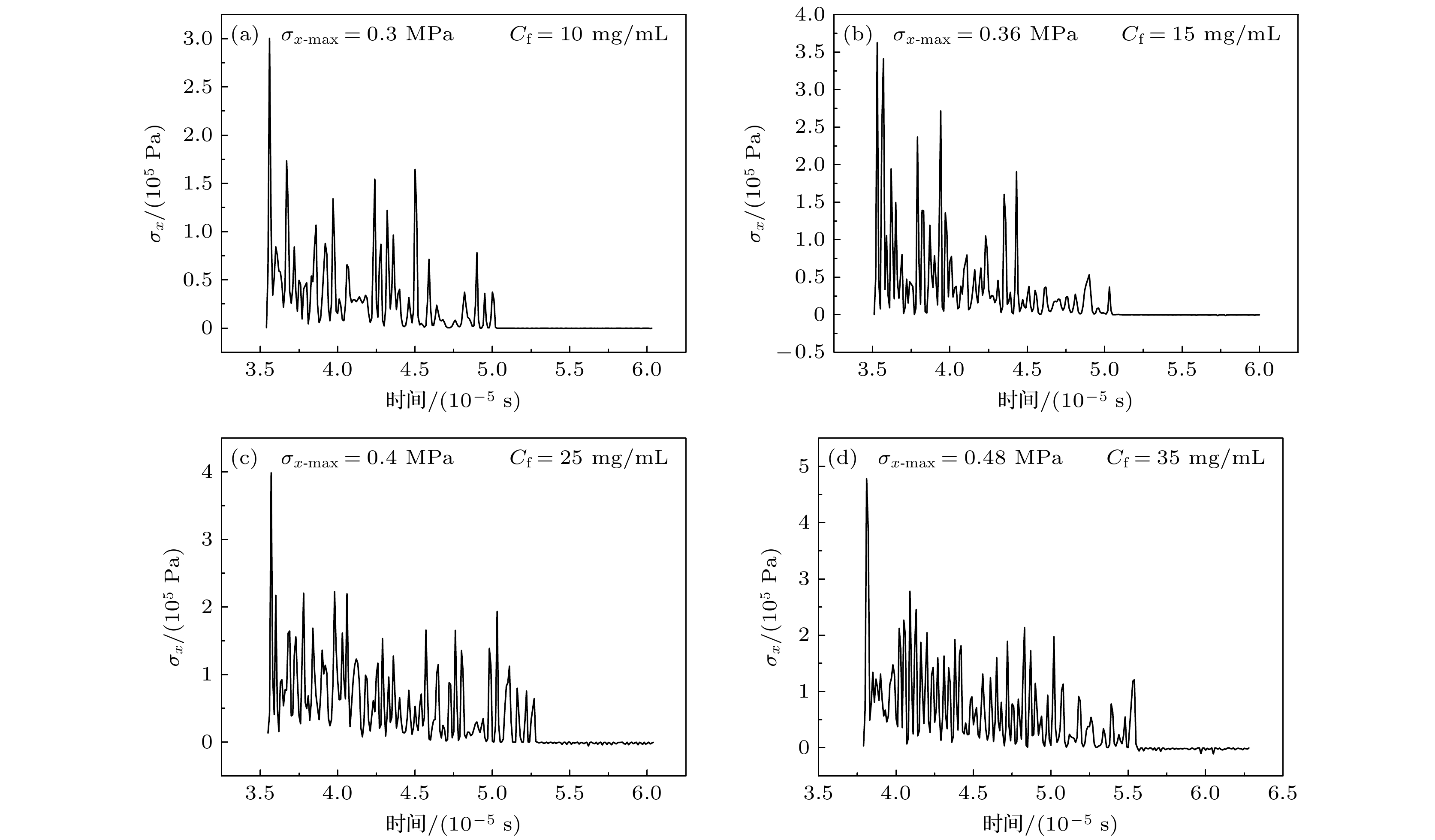
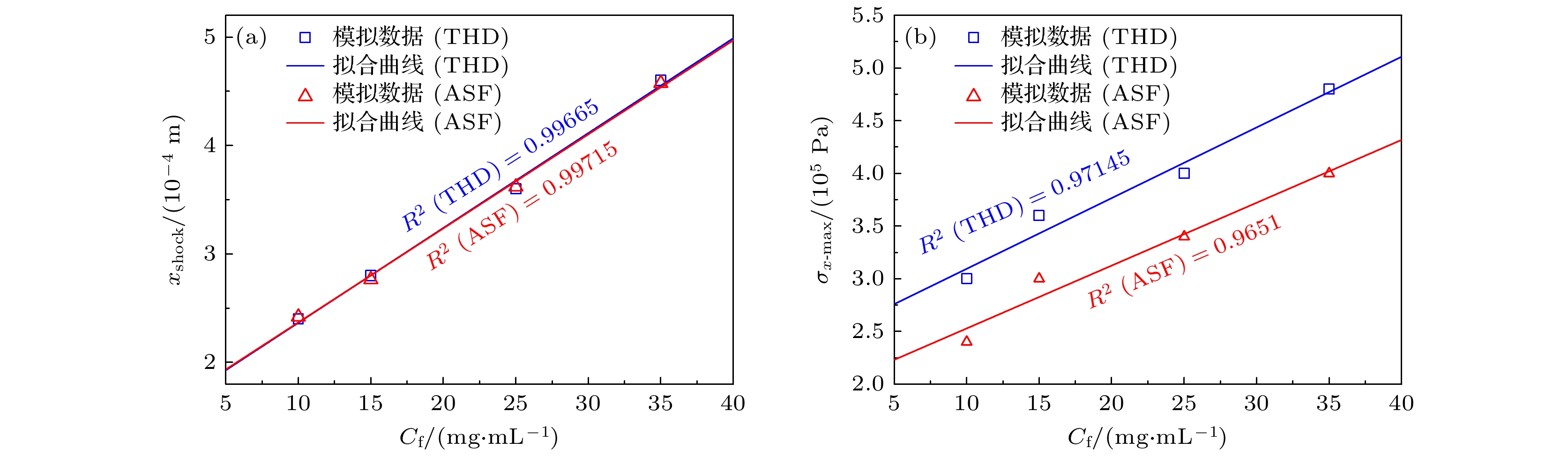
-
虽然空化效应与机械效应在超声溶栓中的作用机制已得到充分证实和深入研究, 但是对于血栓类生物材料, 其浓度依赖的应变硬化特性对超声诱导冲击波效应的影响仍受到广泛关注. 其中, 快速的冲击波形成的空间定位与能量阈值的确定对临床治疗方案的优化具有重要指导价值. 本研究通过准静态单轴压缩实验, 建立了纤维蛋白浓度依赖的幂律本构模型. 基于凝块本构方程与非线性波动方程, 研究了超声在凝块介质中传播的动力学特性. 数值模拟结果表明: 冲击波形成前的应力强间断现象源于凝块渐增硬化特性导致的位移突变; 基于阈值限制的平均陡峭因子冲击波定位判据受网格收敛性严重制约, 而总谐波失真截断误差敏感性相对较低, 基于THD定位判据的峰值应力显著高于前者且具有计算成本优势. 参数化研究表明, 纤维蛋白浓度增大导致冲击波形成位置延后且峰值应力增大. 本研究为临床超声溶栓治疗中冲击波效应的快速定位和灵活调控提供了理论依据.
Ultrasound thrombolysis stands out among various treatment methods due to its safety and high efficiency. Although the cavitation and mechanical mechanisms behind this technique have been well-established, the effect of the concentration-dependent strain hardening properties of thrombotic biomaterials on ultrasound-induced shockwave effects remains a subject of concern. Furthermore, the extremely short time window for effective clinical intervention requires precise spatial localization of rapidly formed shockwaves and determination of their energy thresholds for optimizing treatment protocols. Considering that the main mechanical properties of blood clots are dominated by the fibrin network, their stress-strain relationship is significantly dependent on fibrin concentration. Based on the results obtained from quasi-static compression tests performed on clots with different fibrin concentrations, a power-law constitutive equation capable of characterizing the progressive hardening characteristics of clots is proposed in this work. By incorporating the changes in wave speed caused by strain-hardening characteristics into a third-order nonlinear ultrasound propagation wave equation, the dynamic characteristics of shock wave formation during ultrasound propagation in clot media are studied via numerical simulations. The results show that the significant stress discontinuity prior to this process is due to a sudden displacement change caused by the progressive hardening of the clot. In order to accurately locate the starting position, the average steepening factor (ASF) based on threshold limitation is used for localization. However, this method is severely limited by the problem of mesh convergence, and the improvement in finite accuracy leads to an exponential increase in computation time. In contrast, the total harmonic distortion (THD) using the extremum of frequency-domain energy for localization is less sensitive to truncation errors and provides computational efficiency advantages. Parametric analysis indicates that a maximum localization error between the two methods is 2.55%, and the peak stress determined by the THD criterion is much higher than that determined by the ASF method. Based on experimental fitting of constitutive equations at different concentrations, numerical simulations of wave propagation show that according to the THD criterion, the increase in fibrin concentration from 10 mg/mL to 35 mg/mL delays the formation of shockwave by 91.7% and increases the peak stress by 60%. Corresponding fitting formulas are derived. Through real-time THD feedback and acoustic field parameter adjustment, a theoretical basis is provided for rapidly localizing and flexibly controlling shockwave effects in clinical ultrasound thrombolysis. -
Keywords:
- ultrasonic thrombolysis /
- shock wave effects /
- increasingly hardening material /
- average steepening factor
[1] Chen C Y, Zhou L L, Ying J 2023 Chin. Modern Med. 30 27 (in Chinses) [陈春燕, 周兰兰, 应杰 2023 中国当代医药 30 27]
Google Scholar
Chen C Y, Zhou L L, Ying J 2023 Chin. Modern Med. 30 27 (in Chinses)
Google Scholar
[2] Amuluru K, Nguyen J, Al-Mufti F, Denardo A, Scott J, Yavagal D, Sahlein D H 2022 J. Stroke Cerebrovasc. 31 106553
Google Scholar
[3] Nedelmann M, Eicke B M, Lierke E G, Heimann A, Kempski O, Hopf H C 2002 J. Ultras. Med. 21 649
Google Scholar
[4] Behrens S, Daffertshofer M, Spiegel D, Hennerici M 1999 Ultrasound Med. Biol. 25 269
Google Scholar
[5] 钱骏, 谢伟, 周小伟, 谭坚文, 王智彪, 杜永洪, 李雁浩 2022 71 037201
Google Scholar
Qian J, Xie W, Zhou X W, Tan J W, Wang Z B, Du Y H, Li Y H 2022 Acta Phys. Sin. 71 037201
Google Scholar
[6] Chernysh I N, Everbach C E, Purohit P K, Weisel J W 2015 J. Thromb. Haemost. 13 601
Google Scholar
[7] Datta S, Coussios C C, McAdory L E, Tan J, Porter T, De Courten-Myers G, Holland C K 2006 Ultrasound Med. Biol. 32 1257
Google Scholar
[8] Kagami S, Kanagawa T 2022 Ultrason. Sonochem. 88 105911
Google Scholar
[9] 许龙, 汪尧 2023 72 024303
Google Scholar
Xu L, Wang Y 2023 Acta Phys. Sin. 72 024303
Google Scholar
[10] Wang X B, Wang H L, Wu M Q, Li L L, Zhao B 2024 Ceram. Int. 50 42247
Google Scholar
[11] Meng B, Cao B N, Wan M, Wang C J, Shan D B 2019 Int. J. Mech. Sci. 157–158 609
Google Scholar
[12] 陈赵江, 张淑仪, 郑凯 2010 59 4071
Google Scholar
Chen Z J, Zhang S Y, Zheng K 2010 Acta Phys. Sin. 59 4071
Google Scholar
[13] Zhao J J, Su H, Wu C S 2020 J. Mater. Res. Technol. 9 14895
Google Scholar
[14] Meng Y, Ma L F, Jia W T, Huang Z Q, Xie H B, Ning F K, Lei J Y 2024 J. Mater. Res. Technol. 28 2138
Google Scholar
[15] Johnson S, McCarthy R, Gilvarry M, McHugh P E, McGarry J P 2021 Ann. Biomed. Eng. 49 420
Google Scholar
[16] Piechocka I K, Bacabac R G, Potters M, MacKintosh F C, Koenderink G H 2010 Biophys. J. 98 2281
Google Scholar
[17] Ramanujam R K, Maksudov F, Litvinov R I, Nagaswami C, Weisel J W, Tutwiler V, Barsegov V 2023 Adv. Healthcare Mater. 12 2300096
Google Scholar
[18] Ariëns R A, Sharp A S, Duval C 2024 Haematol-hematol J. 110 21
Google Scholar
[19] Adzerikho I E, Mrochek A G, Minchenya V T, Dmitriev V V, Kulak A I 2011 Ultrasound Med. Biol. 37 1644
Google Scholar
[20] Adzerikho I, Kulak A, Rachok S, Minchenya V 2022 Ultrasound Med. Biol. 48 846
Google Scholar
[21] Tang J H, Tang J W, Liao Y Y, Bai L H, Luo T T, Xu Y L, Liu Z 2024 Heliyon 10 e26624
Google Scholar
[22] Cherniavsky E A, Strakha I S, Adzerikho I E, Shkumatov V M 2011 BMC Biochem 12 60
Google Scholar
[23] Roohi R, Baroumand S, Hosseinie R, Ahmadi G 2021 Int. Commun. Heat Mass 120 105002
Google Scholar
[24] Purrington R D, Norton G V 2012 Math. Comput. Simulat. 82 1287
Google Scholar
[25] Sheng R Z, Zhang J 2022 Appl. Acoust. 195 108867
Google Scholar
[26] Ramos J I 2020 Int. J. Eng. Sci. 149 103226
Google Scholar
[27] Alarcón H, Galaz B, Espíndola D 2025 Ultrasonics 145 107469
Google Scholar
[28] Qu J M 2025 Ultrasonics 151 107621
Google Scholar
[29] Muhlestein M B, Gee K L, Nielsen T B, Thomas D C 2013 J. Acoust. Soc. Am. 134 3981
Google Scholar
[30] Muhlestein M B, Gee K L, Neilsen T B, Thomas D C 2015 J. Acoust. Soc. Am. 137 640
Google Scholar
[31] Ren W J, Xie W J, Zhang Y, Yu H, Tian Z Y 2025 J. Comput. Phys. 523 113649
Google Scholar
[32] Nguyen N C, Van Heyningen R L, Vila-Pérez J, Peraire J 2024 J. Comput. Phys. 508 113005
Google Scholar
[33] Malkin R, Kappus B, Long B, Price A 2023 J. Sound Vib. 552 117644
Google Scholar
[34] Pattofatto S, Elnasri I, Zhao H, Tsitsiris H, Hild F, Girard Y 2007 J. Mech. Phys. Solids 55 2672
Google Scholar
[35] Zhao G L, Liu S Z, Zhang C, Jin L, Yang Q X 2022 Vacuum 197 110841
Google Scholar
[36] Norris A N 2024 Nonlinear Acoustics (Cham: Springer Nature Switzerland) p259
[37] Thurston R N 1974 Mechanics of Solids (Berlin: Springer Verlag) p109
[38] 王礼立 2005 应力波基础(第2版) (北京: 国防工业出版社) 第7页
Wang L L 2005 Foundation of Stress Waves (Vol. 2) (Beijing: National Defense Industry Press) p7
[39] 杜功焕 2001 声学基础(第2版)(江苏: 南京大学出版社) 第479页
Du G H 2001 Foundation of Acoustics (Vol. 2) (Jiangsu: Nanjing University Press) p479
[40] Xia L 2019 J. Acoust. Soc. Am. 146 1394
Google Scholar
[41] 牛金海 2017 超声原理及生物医学工程应用(第2版) (上海: 上海交通大学出版社) 第11页
Niu H J 2017 Principles of Ultrasound and Applications in Biomedical Engineering (Vol. 2) (Shanghai: Shanghai Jiao Tong University Press) p11
[42] 龚秀芬, 章东 2005 应用声学 24 208
Google Scholar
Gong X F, Zhang D 2005 J. Appl. Acoust 24 208
Google Scholar
[43] Tutwiler V, Maksudov F, Litvinov R I, Weisel J W, Barsegov V 2021 Acta Biomater. 131 355
Google Scholar
[44] Depalle B, Qin Z, Shefelbine S J, Buehler M J 2015 J. Mech. Behav. Biomed. Mater. 52 1
Google Scholar
[45] Sekkal W, Zaoui A, Benzerzour M, Abriak N 2016 Cem. Concr. Res. 87 45
Google Scholar
-
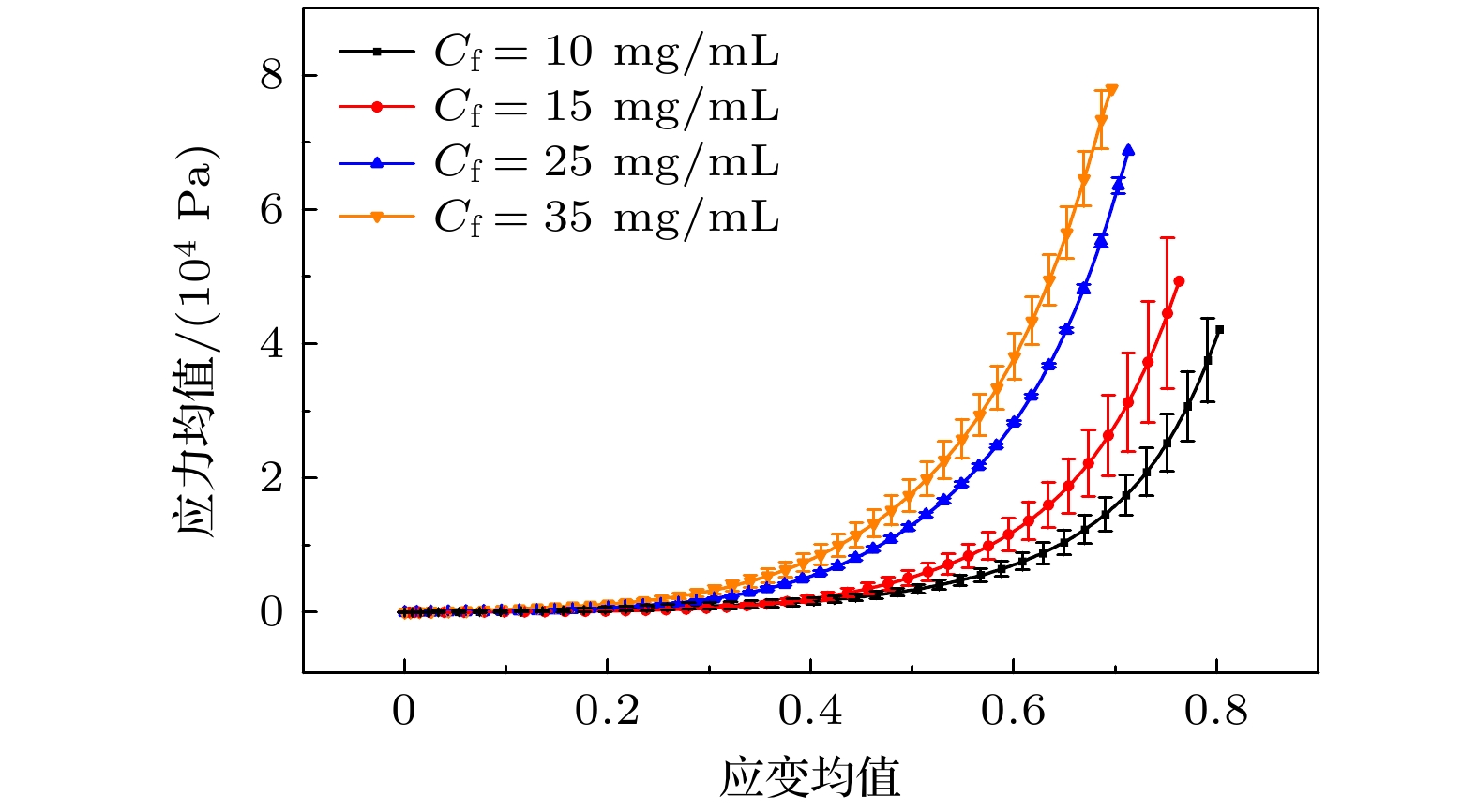
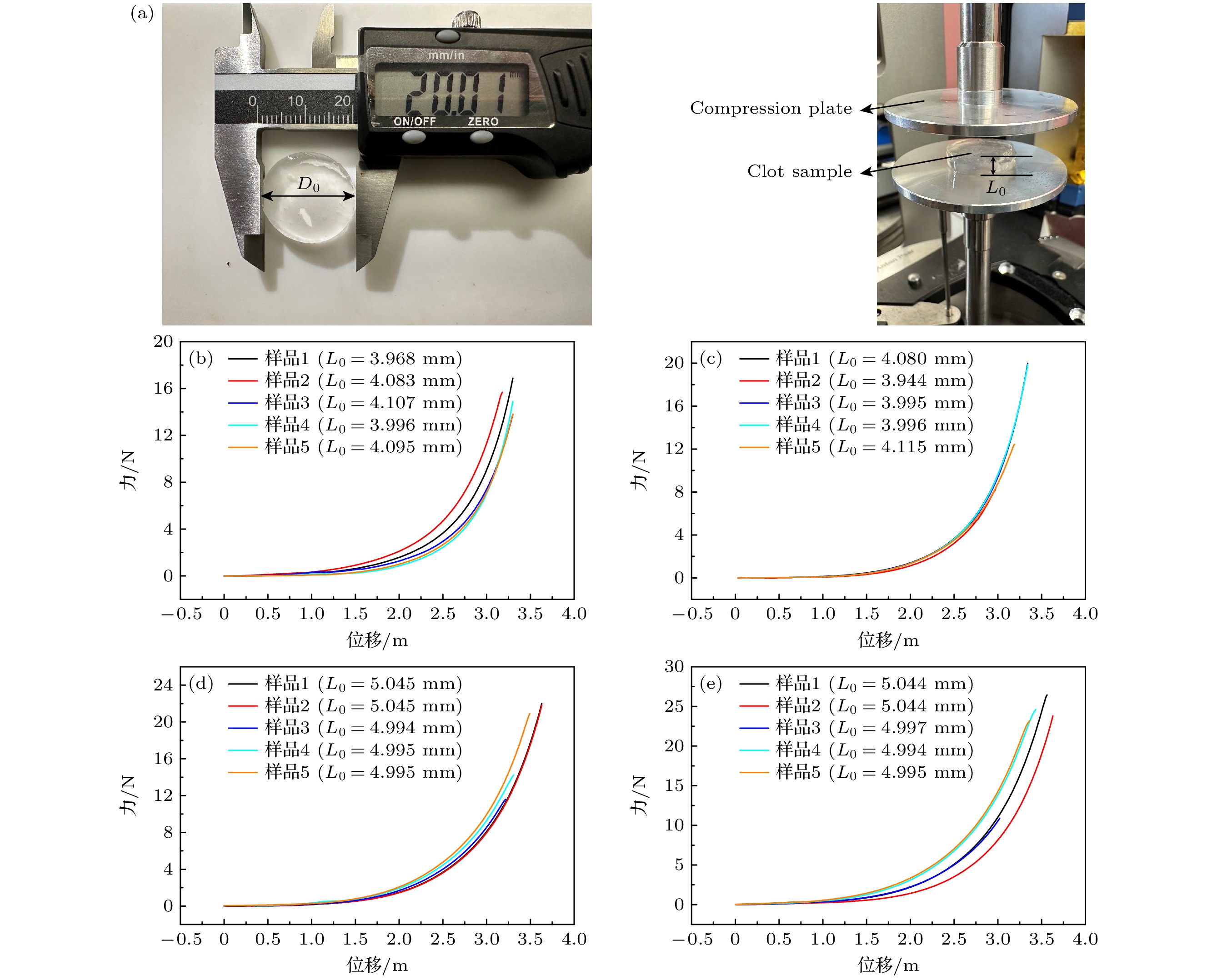
图 1 (a) 不同厚度$ {L_0} $的凝块样品(直径$ {D_0} = 20\;{\mathrm{mm}} $)及压缩试验平台; (b)—(e) 不同浓度的力-位移曲线((b) 10 mg/mL, (c) 15 mg/mL, (d) 25 mg/mL, (e) 35 mg/mL)
Fig. 1. (a) Clot samples of different thicknesses $ {L_0} $(diameter $ {D_0} = 20\;{\mathrm{mm}} $) and compression test platform; (b)–(e) force displacement curves at different concentrations ((b) 10 mg/mL, (c) 15 mg/mL, (d) 25 mg/mL, (e) 35 mg/mL).
图 2 不同浓度应力-应变曲线的误差棒分析
Fig. 2. Error bar analysis of stress-strain curves at different concentrations.
图 3 实验的力-位移曲线及应力-应变拟合图
Fig. 3. Experimental force displacement curves and stress-strain fitting diagram.
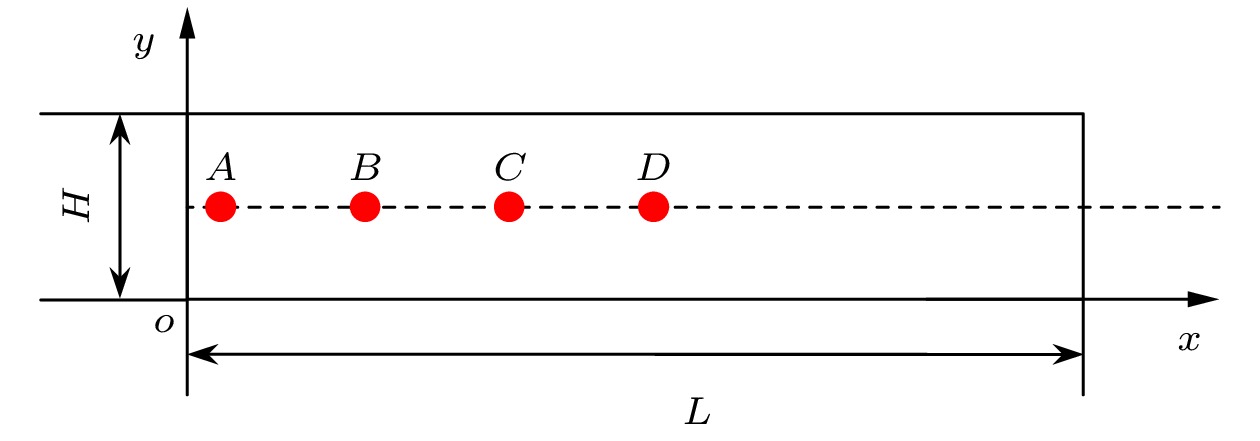
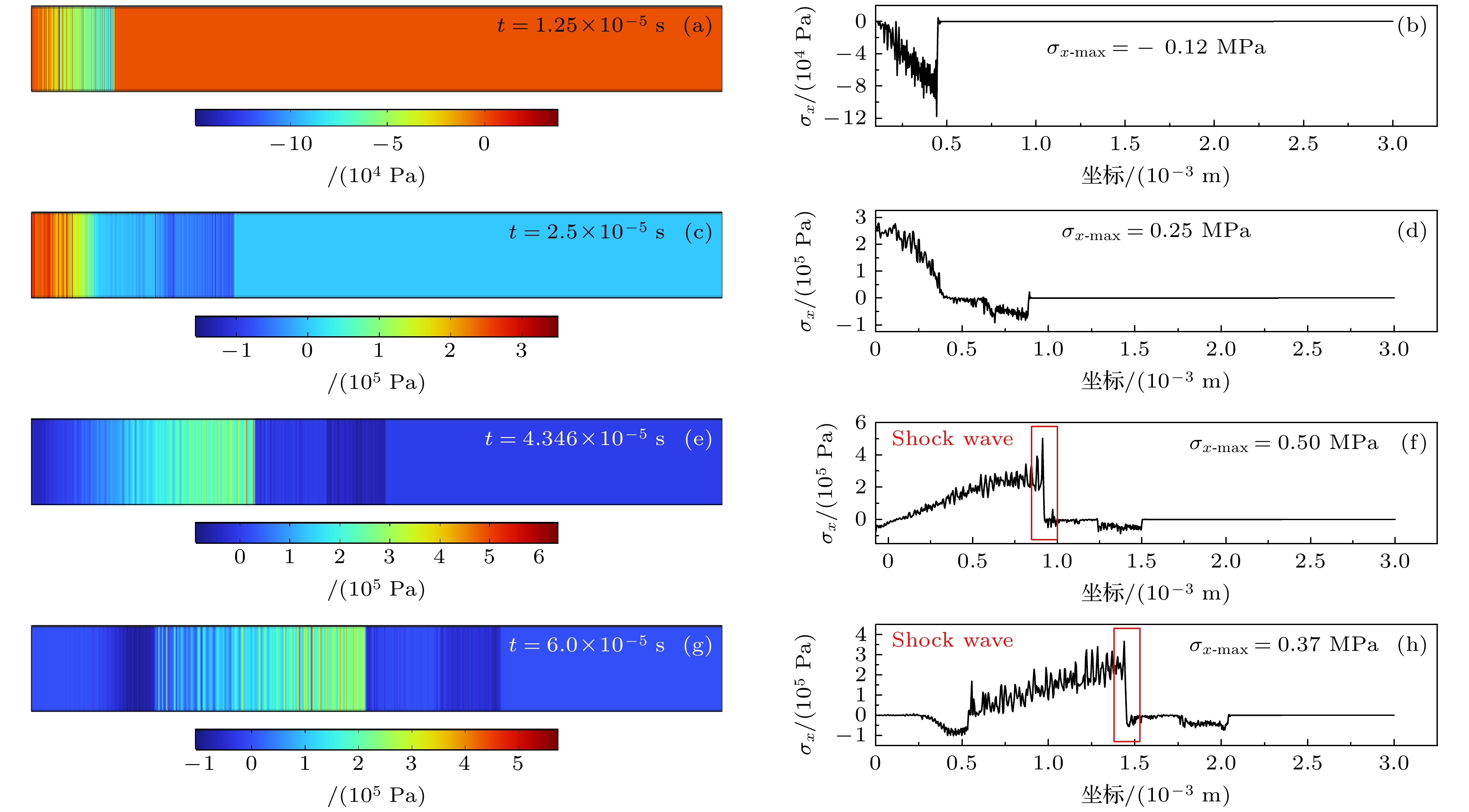
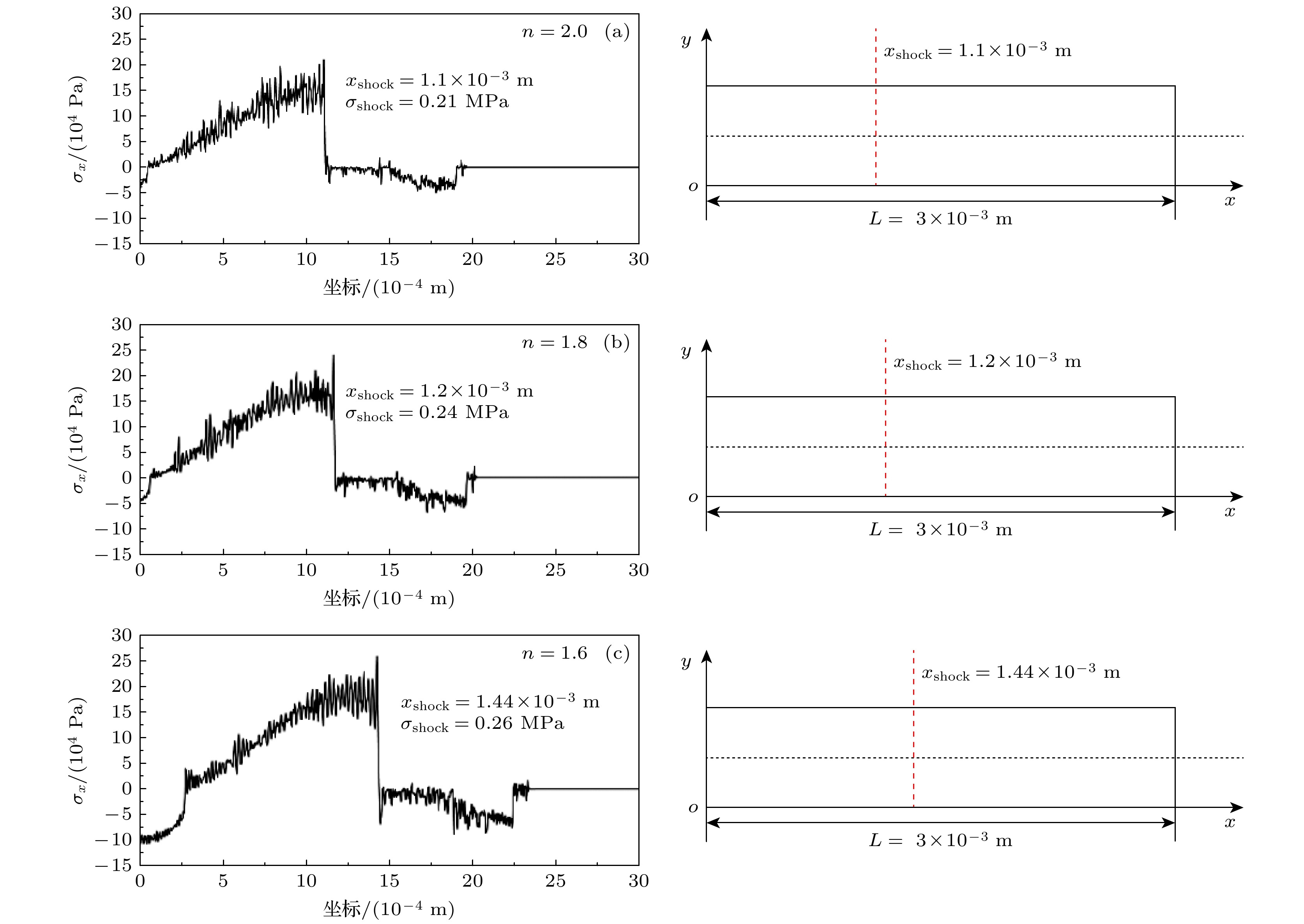
图 5 二维模型波传播示意图(频率f = 20 kHz, 硬化指数n = 2, 硬化系数k = 1.0 MPa, 非线性参量比值$ \beta /\gamma =5,~\beta =-5$, $\gamma = -1$)
Fig. 5. Schematic diagram of two-dimensional model wave propagation (Frequency f = 20 kHz, hardening index n = 2, hardening coefficient k = 1.0 MPa, nonlinear parameter ratio $ \beta /\gamma =5, \beta =-5, \gamma =-1 $).
图 10 不同纤维蛋白浓度对THD数的影响
Fig. 10. Influence of different fibrin concentrations on THD parameters.
图 11 纤维蛋白浓度对最大应力的影响 (a) Cf = 10 mg/mL; (b) Cf = 15 mg/mL; (c) Cf = 25 mg/mL; (d) Cf = 35 mg/mL
Fig. 11. Effect of fibrin concentration on maximum stress: (a) Cf = 10 mg/mL; (b) Cf = 15 mg/mL; (c) Cf = 25 mg/mL; (d) Cf = 35 mg/mL.
图 12 模型中段冲击波示意图
Fig. 12. Schematic diagram of shock wave in the middle section of the model.
图 13 纤维蛋白浓度对冲击波形成位置(a)和最大应力(b)的影响
Fig. 13. Influence of fibrin concentration on the location (a) and maximum stress (b) of shock wave formation.
表 1 不同浓度的误差棒分析
Table 1. Error bar analysis of different concentrations.
纤维蛋白浓度Cf/(mg·mL–1) 最大相对标准差/% 10
15
2516.6
26.2
2.6635 5.76 
下载: 导出CSV
表 2 模型的物性参数
Table 2. Physical property parameters of the model.
参数 描述 数值 $ {\rho _0} $/(kg·m–3) 凝块密度 1050 $ {U_0} $/m 振幅 1 × 10–4 $ \alpha $ 无量纲系数 6.1 $ \kappa $/(kPa·mg–1·mL) 比例系数 1.2 $ \eta $ 幂指数 1.8
下载: 导出CSV
表 3 参数化分析
Table 3. Parametric analysis.
频率f / kHz 硬化指数n 比值β/γ
(γ = -1)xASF / m
(ASF = 100)xTHD / m 误差/% 15 2 5 1.12×10–3 1.10×10–3 ≤1.79 25 2 5 7.58×10–4 7.62×10–4 ≤0.53 20 4.84 5 3.61×10–4 3.57×10–4 ≤1.11 20 6.20 5 2.43×10–4 2.38×10–4 ≤2.06 20 2 20 8.06×10–4 7.97×10–4 ≤1.12 20 2 40 7.93×10–4 7.78×10–4 ≤1.89 15 6.20 40 5.48×10–4 5.34×10–4 ≤2.55
下载: 导出CSV
表 4 网格数对ASF数的影响(频率f = 15 kHz, 硬化指数n = 6.2, 硬化系数k = 1.0 MPa, 比值$ \beta /\gamma =40,\beta =-40, $$ \gamma =-1 $)
Table 4. Influence of grid number on ASF (frequency f = 15 kHz, hardening index n = 6.2, hardening coefficient k = 1.0 MPa, nonlinear parameter ratio $ \beta /\gamma =40, \beta =-40, \gamma =-1 $).
i 网格数 计算时长
(20核 AMD Epyc 7763 64-core processor × 256)$ x_i^{{\mathrm{ASF}}} $/m
(ASF = 100)相对误差变化
$ \left( \left( {x_{i - 1}^{\mathrm{ASF}} - x_i^{\mathrm{ASF}}} \right) \left/ x_{i - 1}^{{\mathrm{ASF}}}\right. \right) \big/{\text{%}}$1 6000 24 min 5.48×10–4 — 2 17000 1 h 49 min 5.42×10–4 1.09 3 24000 3 h 39 min 5.40×10–4 0.37 4 37500 6 h 45 min 5.39×10–4 0.19 5 52100 11 h 44 min 5.38×10–4 0.19
下载: 导出CSV
表 5 基频倍数对THD数的影响(频率f = 15 kHz, 硬化指数n = 6.2, 硬化系数k = 1.0 MPa, 比值$ \beta /\gamma =40, $$ \beta =-40,\gamma =-1 $)
Table 5. Influence of fundamental frequency multiples on THD (Frequency f = 15 kHz, hardening index n = 6.2, hardening coefficient k = 1.0 MPa, nonlinear parameter ratio $ \beta /\gamma =40, \beta =-40, \gamma =-1 $).
i 基频
倍数$ x_i^{{\mathrm{THD}}} $ 相对误差变化
$ \left( \left| \left( x_{i - 1}^{{\mathrm{THD}}} - x_i^{{\mathrm{THD}}} \right)\left/ x_{i - 1}^{{\mathrm{THD}}}\right. \right| \right) \big/{\text{%}}$1 6 5.26×10–4 — 2 12 5.30×10–4 0.76 3 18 5.33×10–4 0.57 4 24 5.35×10–4 0.38 5 30 5.36×10–4 0.19
下载: 导出CSV
-
[1] Chen C Y, Zhou L L, Ying J 2023 Chin. Modern Med. 30 27 (in Chinses) [陈春燕, 周兰兰, 应杰 2023 中国当代医药 30 27]
Google Scholar
Chen C Y, Zhou L L, Ying J 2023 Chin. Modern Med. 30 27 (in Chinses)
Google Scholar
[2] Amuluru K, Nguyen J, Al-Mufti F, Denardo A, Scott J, Yavagal D, Sahlein D H 2022 J. Stroke Cerebrovasc. 31 106553
Google Scholar
[3] Nedelmann M, Eicke B M, Lierke E G, Heimann A, Kempski O, Hopf H C 2002 J. Ultras. Med. 21 649
Google Scholar
[4] Behrens S, Daffertshofer M, Spiegel D, Hennerici M 1999 Ultrasound Med. Biol. 25 269
Google Scholar
[5] 钱骏, 谢伟, 周小伟, 谭坚文, 王智彪, 杜永洪, 李雁浩 2022 71 037201
Google Scholar
Qian J, Xie W, Zhou X W, Tan J W, Wang Z B, Du Y H, Li Y H 2022 Acta Phys. Sin. 71 037201
Google Scholar
[6] Chernysh I N, Everbach C E, Purohit P K, Weisel J W 2015 J. Thromb. Haemost. 13 601
Google Scholar
[7] Datta S, Coussios C C, McAdory L E, Tan J, Porter T, De Courten-Myers G, Holland C K 2006 Ultrasound Med. Biol. 32 1257
Google Scholar
[8] Kagami S, Kanagawa T 2022 Ultrason. Sonochem. 88 105911
Google Scholar
[9] 许龙, 汪尧 2023 72 024303
Google Scholar
Xu L, Wang Y 2023 Acta Phys. Sin. 72 024303
Google Scholar
[10] Wang X B, Wang H L, Wu M Q, Li L L, Zhao B 2024 Ceram. Int. 50 42247
Google Scholar
[11] Meng B, Cao B N, Wan M, Wang C J, Shan D B 2019 Int. J. Mech. Sci. 157–158 609
Google Scholar
[12] 陈赵江, 张淑仪, 郑凯 2010 59 4071
Google Scholar
Chen Z J, Zhang S Y, Zheng K 2010 Acta Phys. Sin. 59 4071
Google Scholar
[13] Zhao J J, Su H, Wu C S 2020 J. Mater. Res. Technol. 9 14895
Google Scholar
[14] Meng Y, Ma L F, Jia W T, Huang Z Q, Xie H B, Ning F K, Lei J Y 2024 J. Mater. Res. Technol. 28 2138
Google Scholar
[15] Johnson S, McCarthy R, Gilvarry M, McHugh P E, McGarry J P 2021 Ann. Biomed. Eng. 49 420
Google Scholar
[16] Piechocka I K, Bacabac R G, Potters M, MacKintosh F C, Koenderink G H 2010 Biophys. J. 98 2281
Google Scholar
[17] Ramanujam R K, Maksudov F, Litvinov R I, Nagaswami C, Weisel J W, Tutwiler V, Barsegov V 2023 Adv. Healthcare Mater. 12 2300096
Google Scholar
[18] Ariëns R A, Sharp A S, Duval C 2024 Haematol-hematol J. 110 21
Google Scholar
[19] Adzerikho I E, Mrochek A G, Minchenya V T, Dmitriev V V, Kulak A I 2011 Ultrasound Med. Biol. 37 1644
Google Scholar
[20] Adzerikho I, Kulak A, Rachok S, Minchenya V 2022 Ultrasound Med. Biol. 48 846
Google Scholar
[21] Tang J H, Tang J W, Liao Y Y, Bai L H, Luo T T, Xu Y L, Liu Z 2024 Heliyon 10 e26624
Google Scholar
[22] Cherniavsky E A, Strakha I S, Adzerikho I E, Shkumatov V M 2011 BMC Biochem 12 60
Google Scholar
[23] Roohi R, Baroumand S, Hosseinie R, Ahmadi G 2021 Int. Commun. Heat Mass 120 105002
Google Scholar
[24] Purrington R D, Norton G V 2012 Math. Comput. Simulat. 82 1287
Google Scholar
[25] Sheng R Z, Zhang J 2022 Appl. Acoust. 195 108867
Google Scholar
[26] Ramos J I 2020 Int. J. Eng. Sci. 149 103226
Google Scholar
[27] Alarcón H, Galaz B, Espíndola D 2025 Ultrasonics 145 107469
Google Scholar
[28] Qu J M 2025 Ultrasonics 151 107621
Google Scholar
[29] Muhlestein M B, Gee K L, Nielsen T B, Thomas D C 2013 J. Acoust. Soc. Am. 134 3981
Google Scholar
[30] Muhlestein M B, Gee K L, Neilsen T B, Thomas D C 2015 J. Acoust. Soc. Am. 137 640
Google Scholar
[31] Ren W J, Xie W J, Zhang Y, Yu H, Tian Z Y 2025 J. Comput. Phys. 523 113649
Google Scholar
[32] Nguyen N C, Van Heyningen R L, Vila-Pérez J, Peraire J 2024 J. Comput. Phys. 508 113005
Google Scholar
[33] Malkin R, Kappus B, Long B, Price A 2023 J. Sound Vib. 552 117644
Google Scholar
[34] Pattofatto S, Elnasri I, Zhao H, Tsitsiris H, Hild F, Girard Y 2007 J. Mech. Phys. Solids 55 2672
Google Scholar
[35] Zhao G L, Liu S Z, Zhang C, Jin L, Yang Q X 2022 Vacuum 197 110841
Google Scholar
[36] Norris A N 2024 Nonlinear Acoustics (Cham: Springer Nature Switzerland) p259
[37] Thurston R N 1974 Mechanics of Solids (Berlin: Springer Verlag) p109
[38] 王礼立 2005 应力波基础(第2版) (北京: 国防工业出版社) 第7页
Wang L L 2005 Foundation of Stress Waves (Vol. 2) (Beijing: National Defense Industry Press) p7
[39] 杜功焕 2001 声学基础(第2版)(江苏: 南京大学出版社) 第479页
Du G H 2001 Foundation of Acoustics (Vol. 2) (Jiangsu: Nanjing University Press) p479
[40] Xia L 2019 J. Acoust. Soc. Am. 146 1394
Google Scholar
[41] 牛金海 2017 超声原理及生物医学工程应用(第2版) (上海: 上海交通大学出版社) 第11页
Niu H J 2017 Principles of Ultrasound and Applications in Biomedical Engineering (Vol. 2) (Shanghai: Shanghai Jiao Tong University Press) p11
[42] 龚秀芬, 章东 2005 应用声学 24 208
Google Scholar
Gong X F, Zhang D 2005 J. Appl. Acoust 24 208
Google Scholar
[43] Tutwiler V, Maksudov F, Litvinov R I, Weisel J W, Barsegov V 2021 Acta Biomater. 131 355
Google Scholar
[44] Depalle B, Qin Z, Shefelbine S J, Buehler M J 2015 J. Mech. Behav. Biomed. Mater. 52 1
Google Scholar
[45] Sekkal W, Zaoui A, Benzerzour M, Abriak N 2016 Cem. Concr. Res. 87 45
Google Scholar
下载:
计量
- 文章访问数: 501
- PDF下载量: 11
- 被引次数: 0
