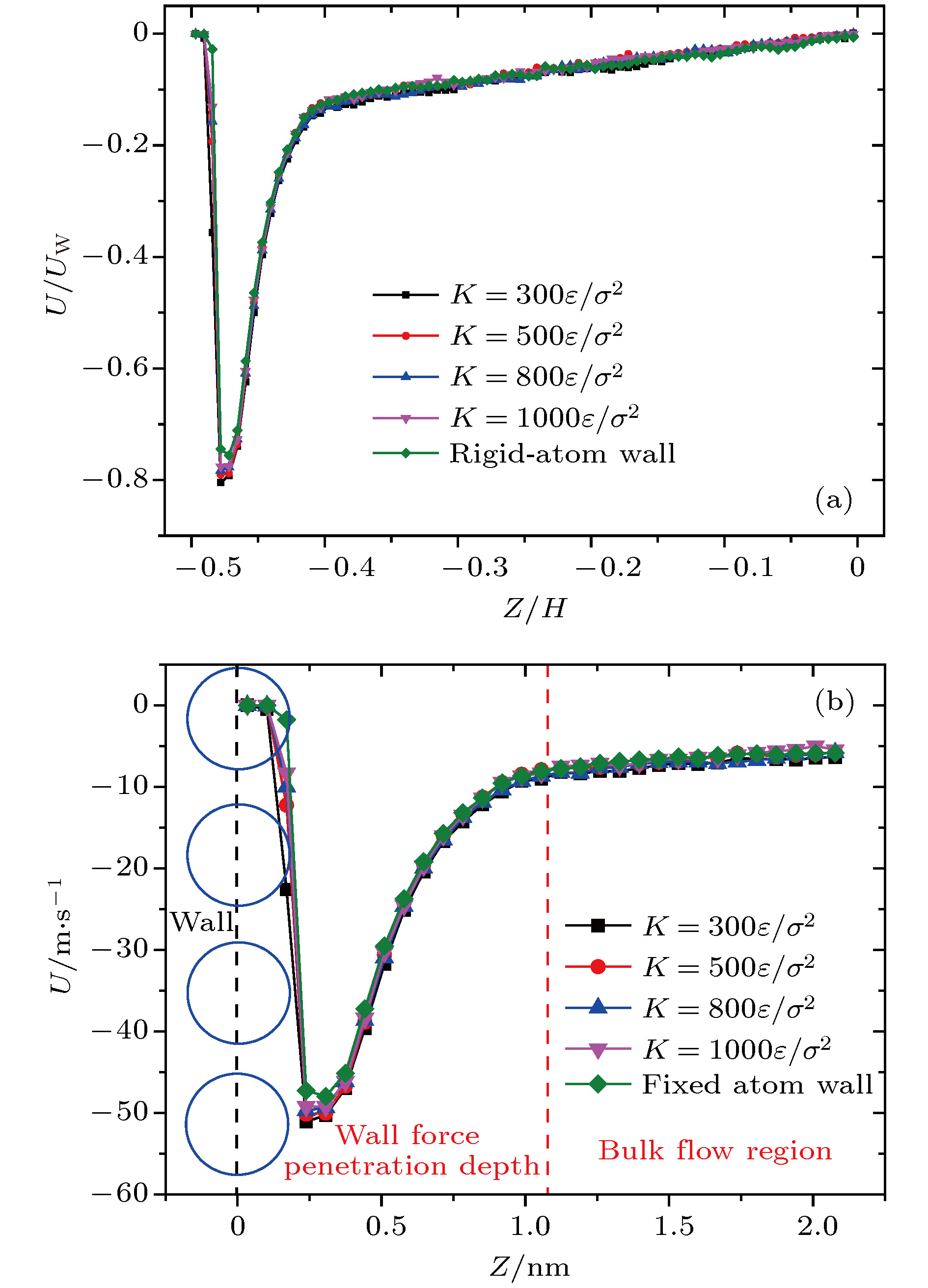
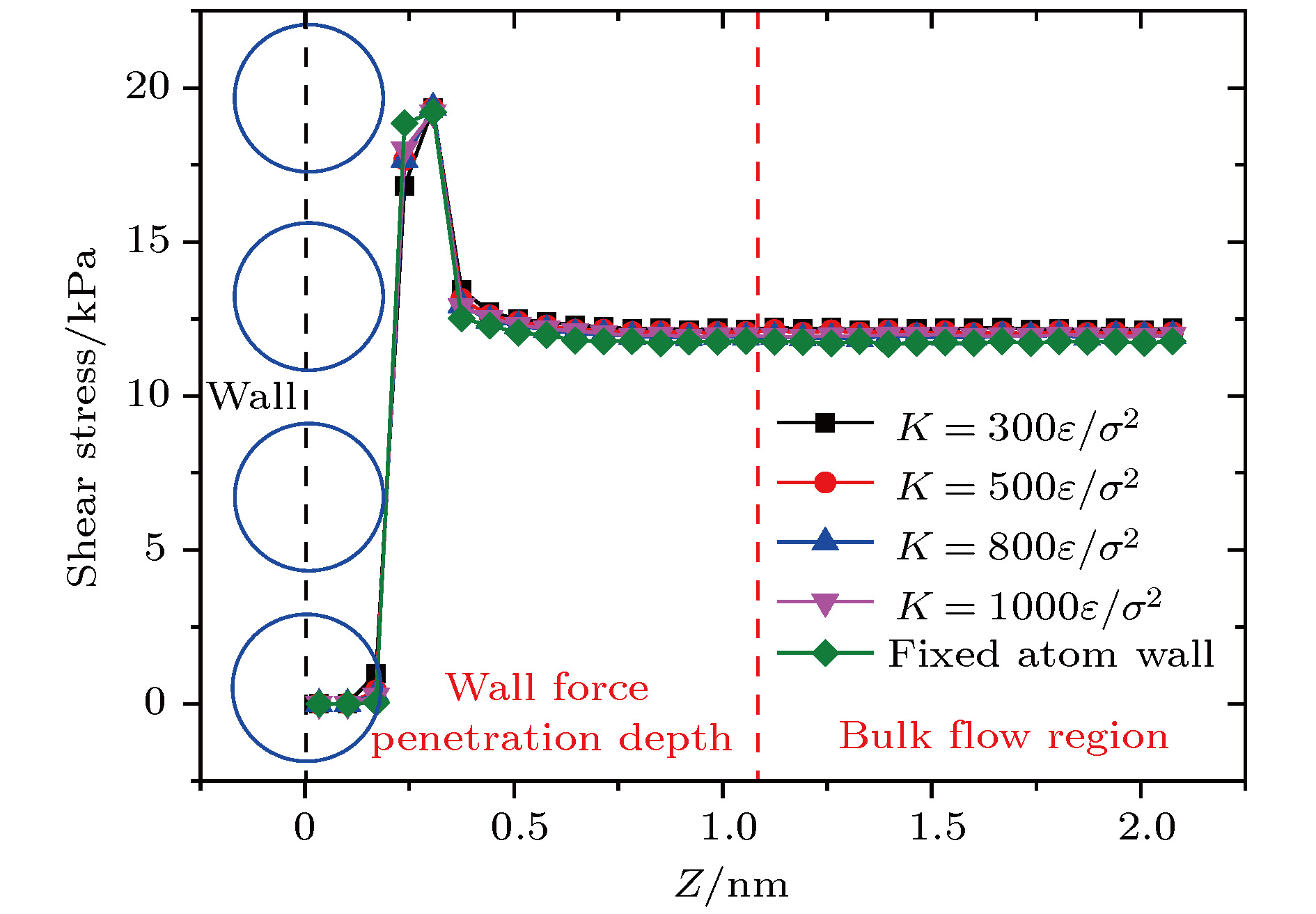
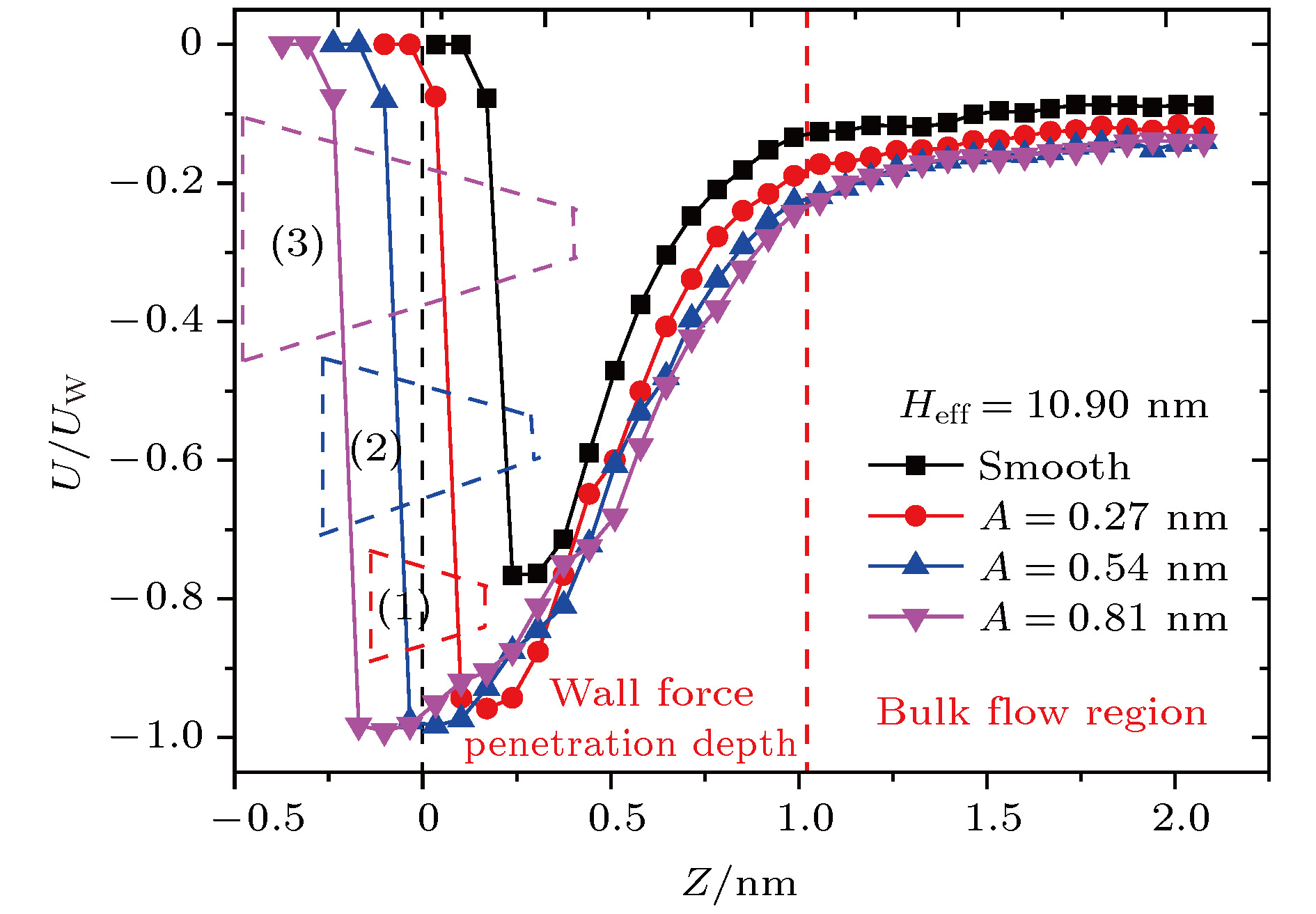
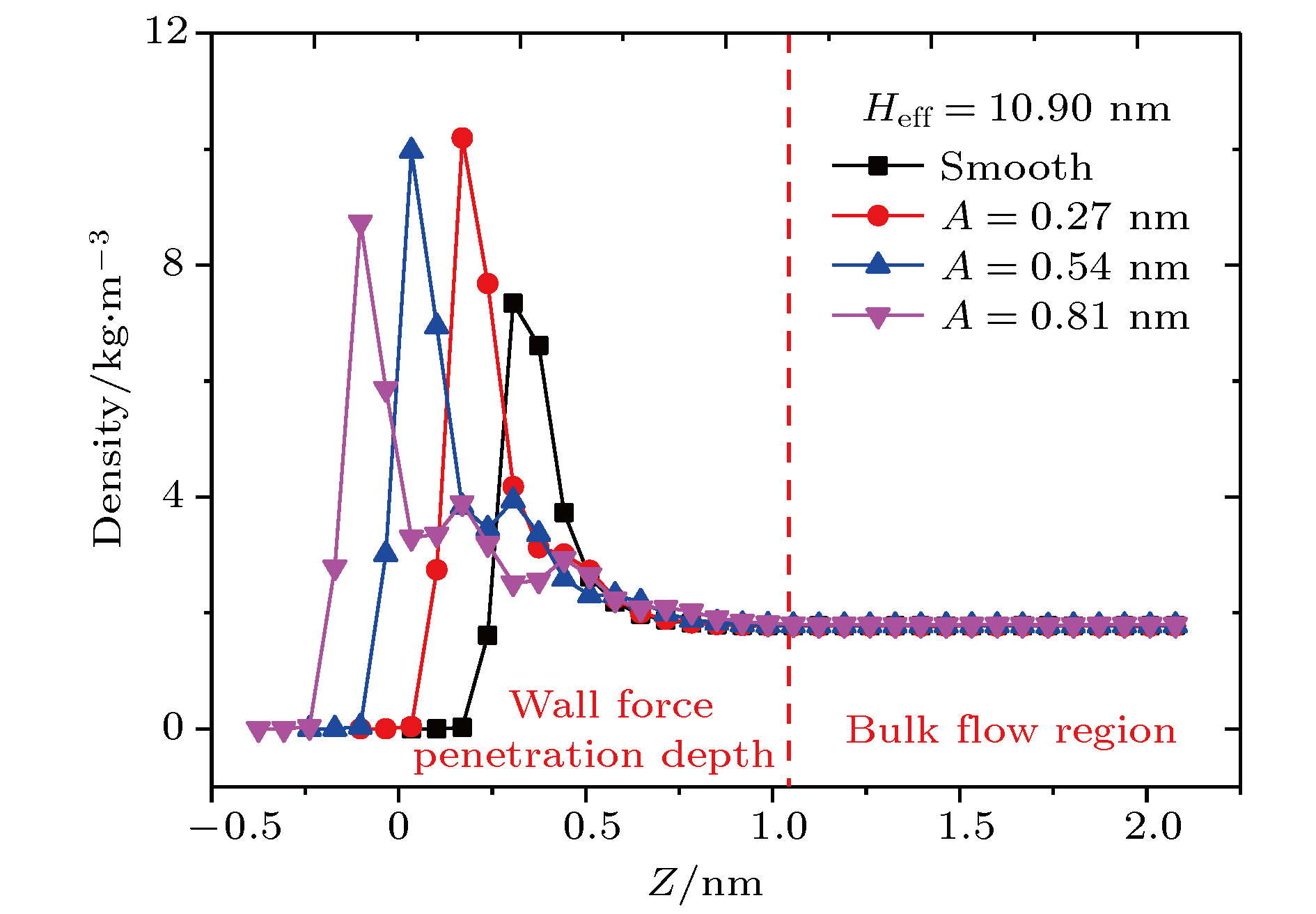
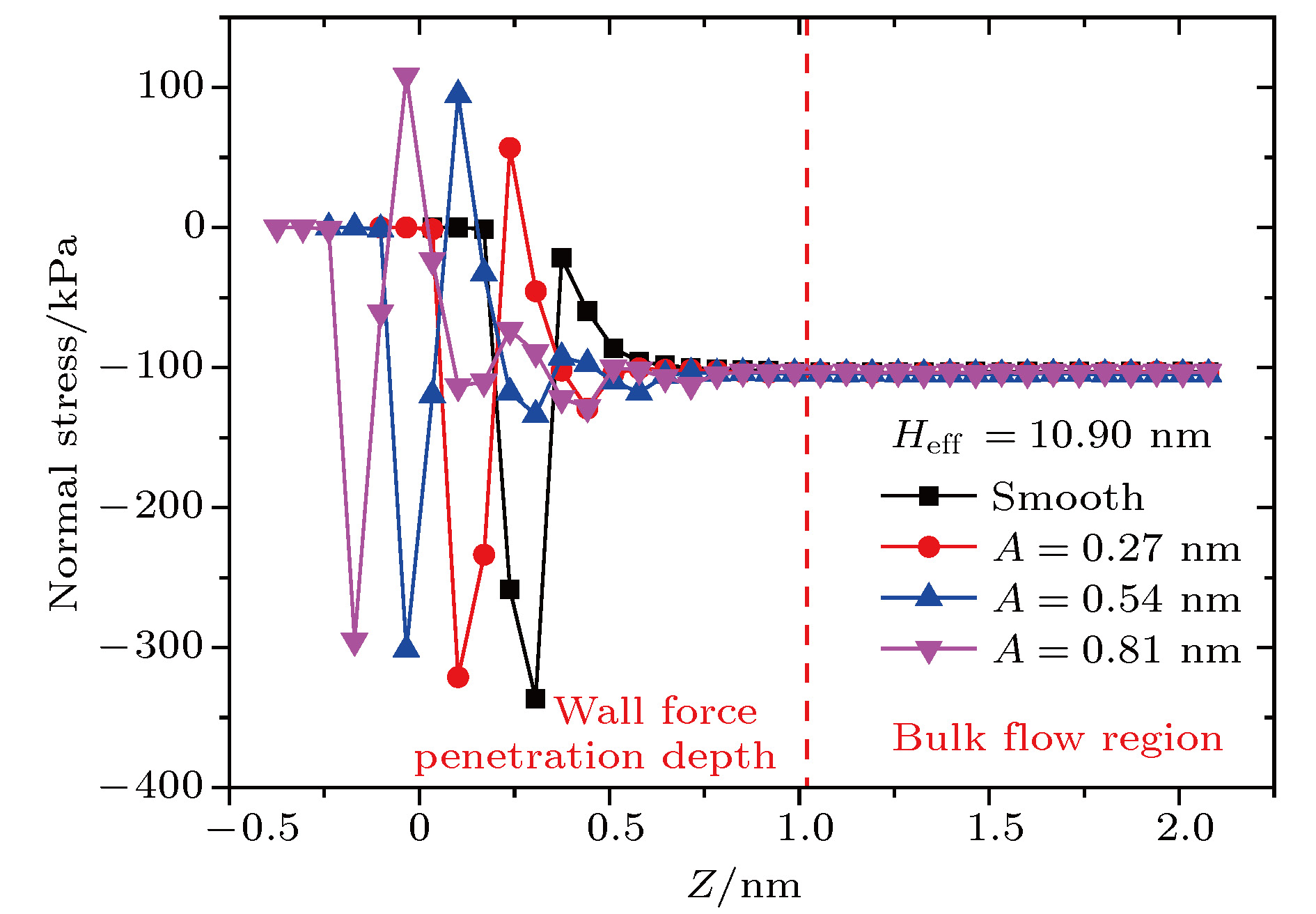
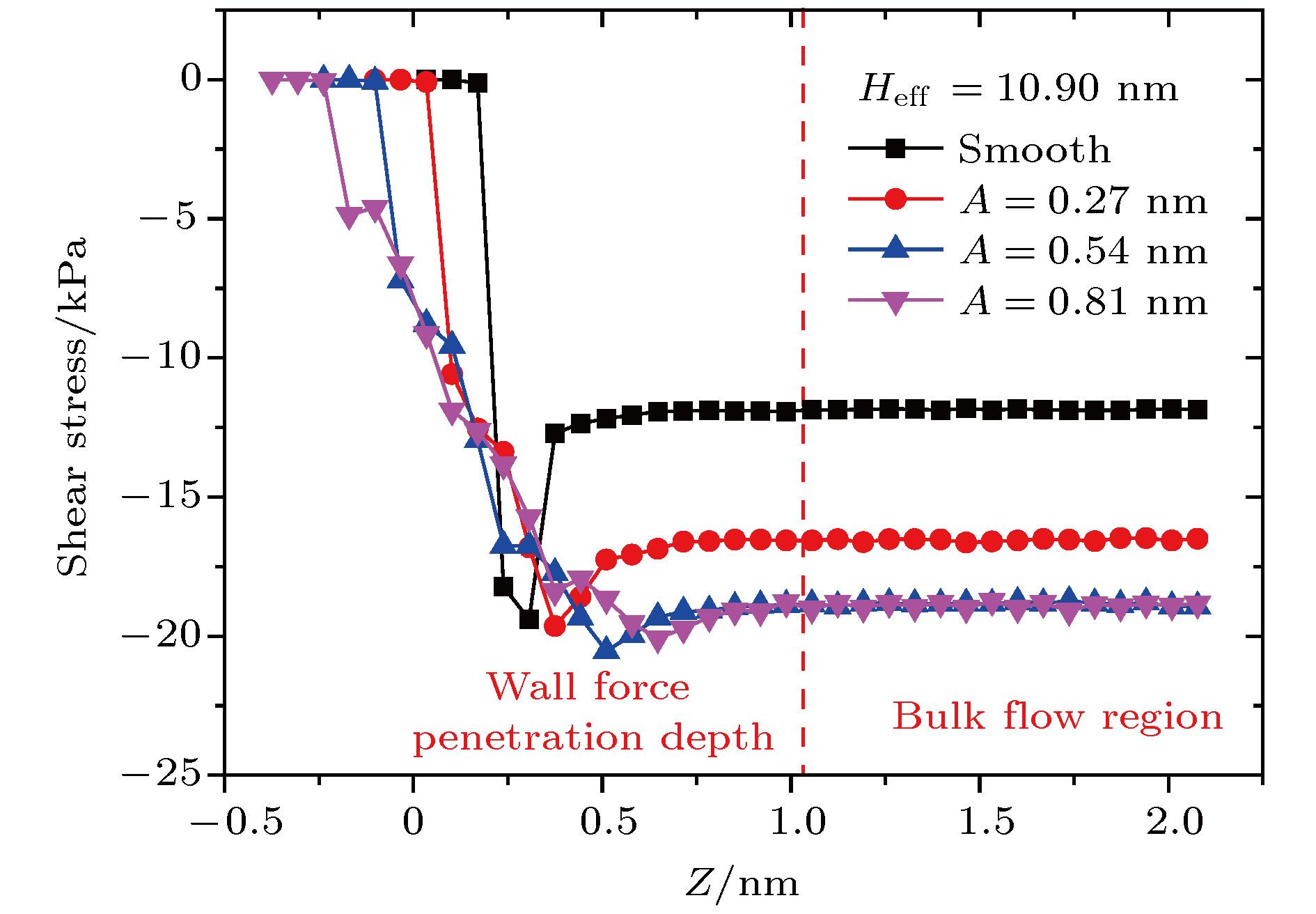
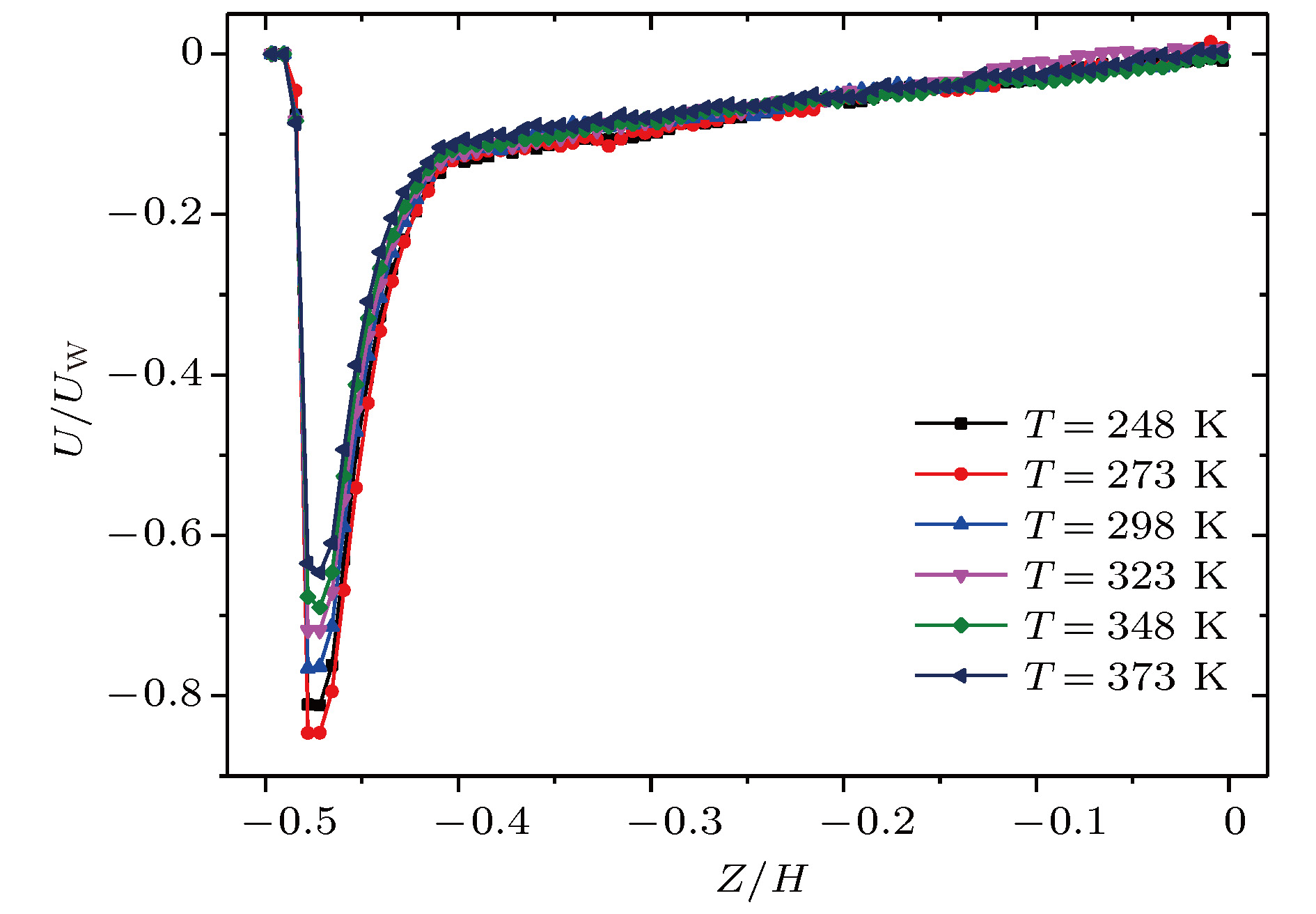
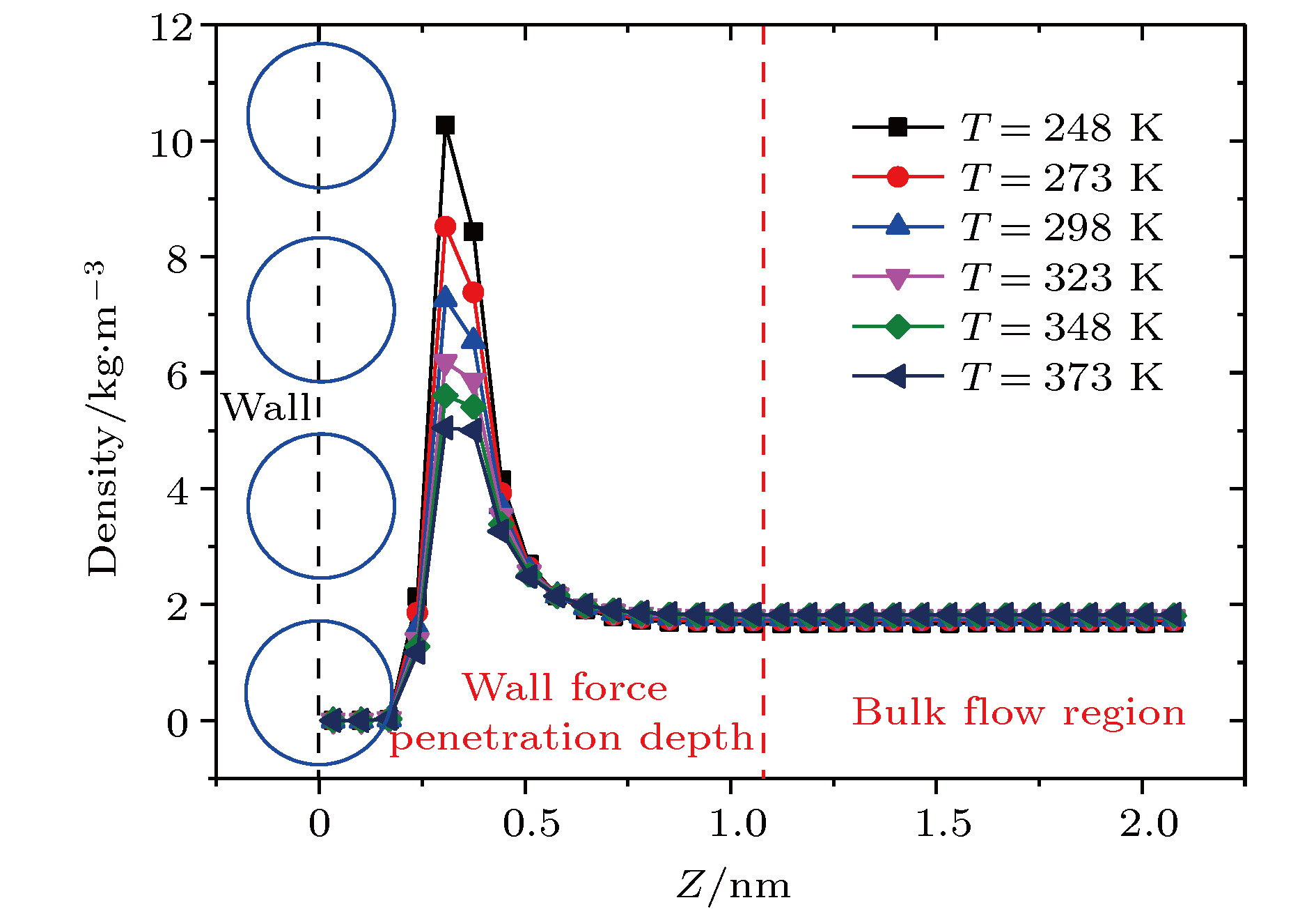
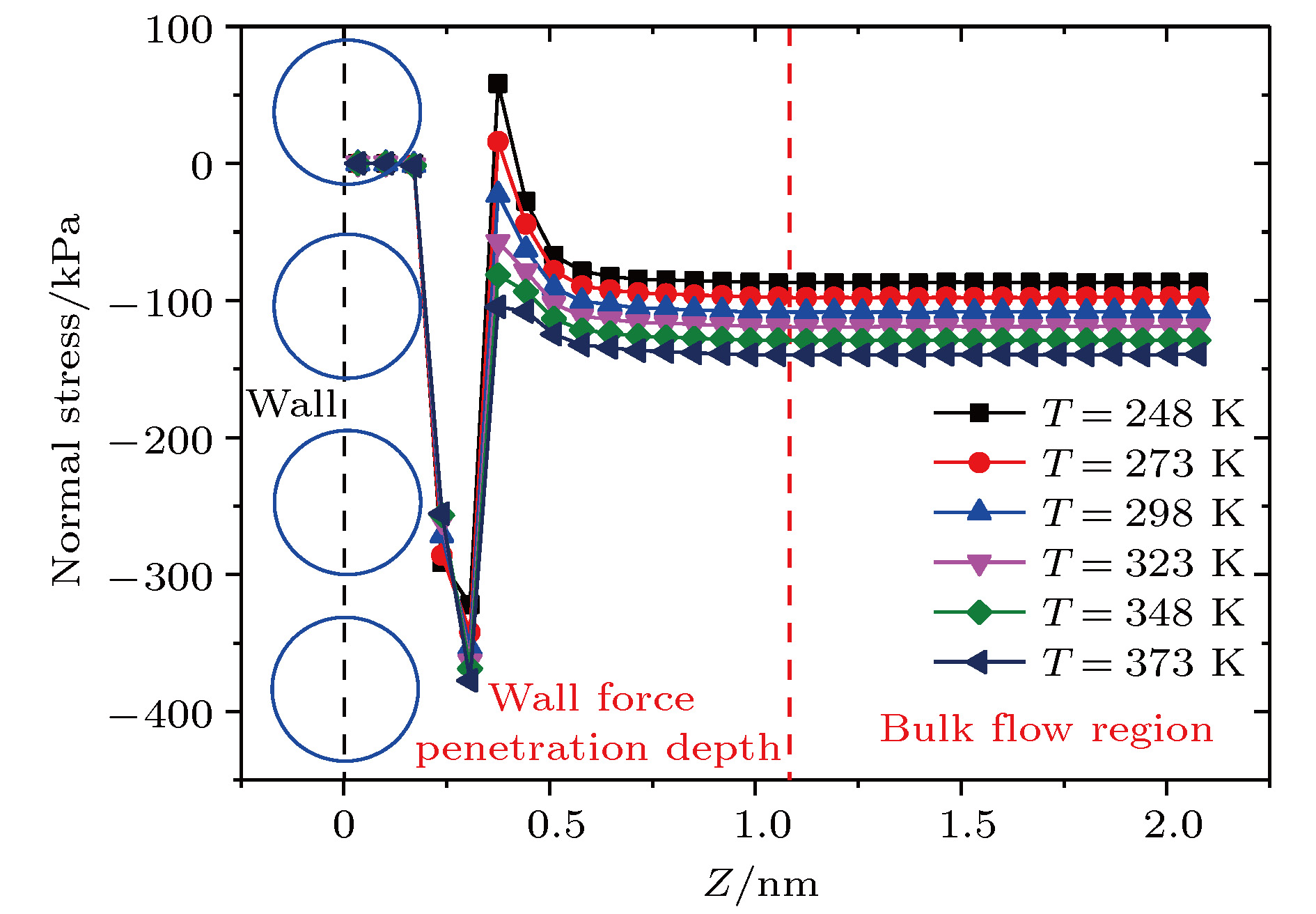
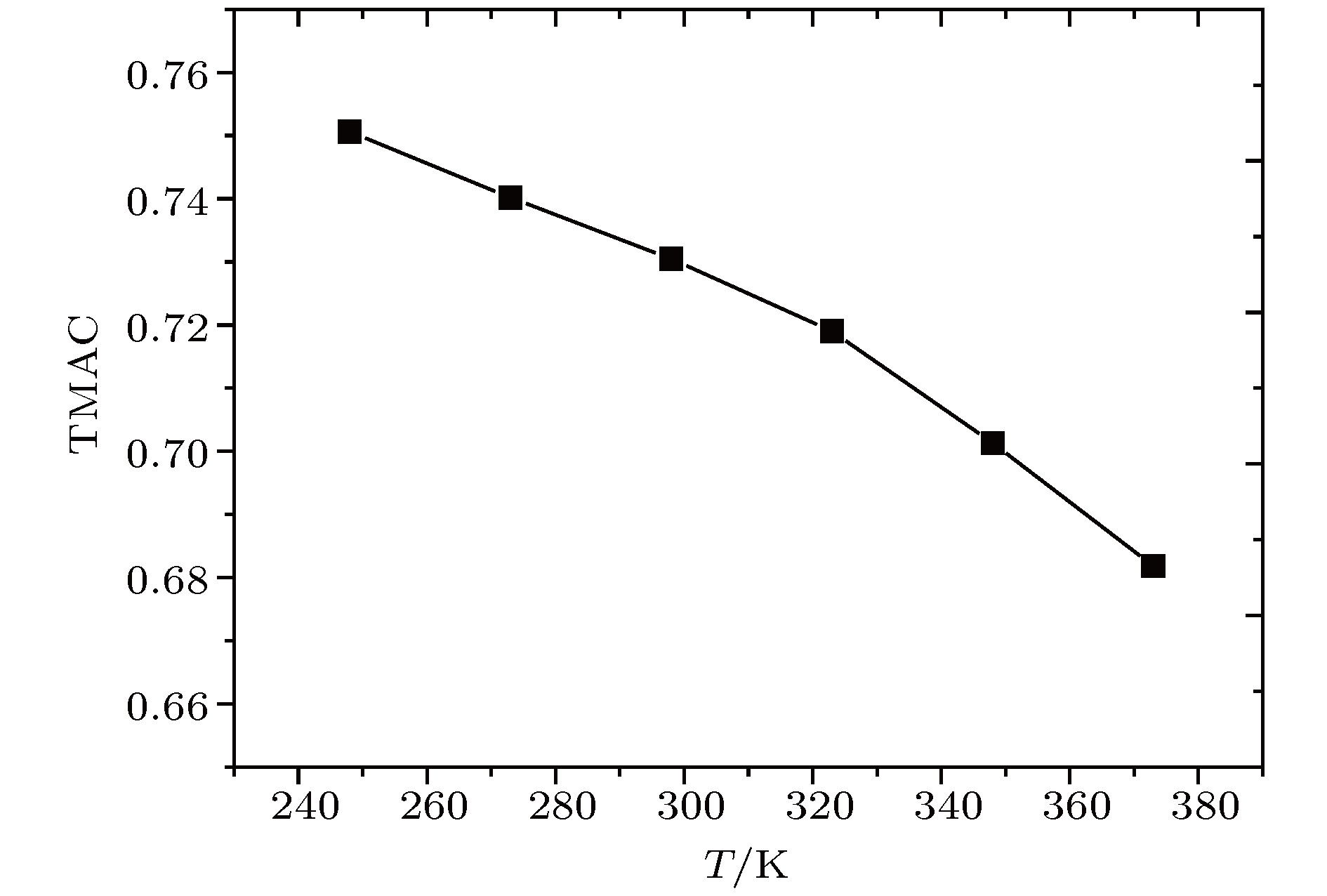
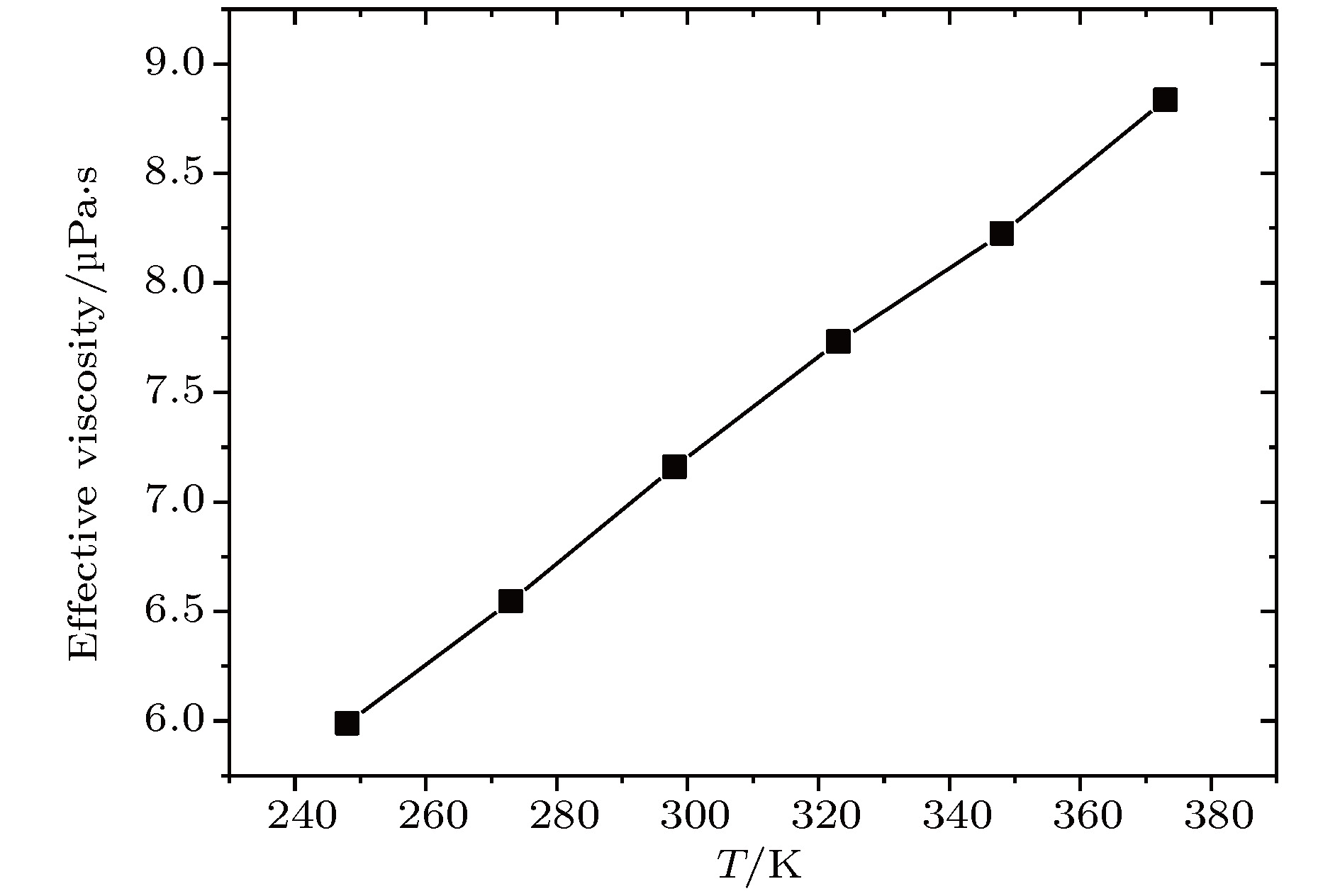
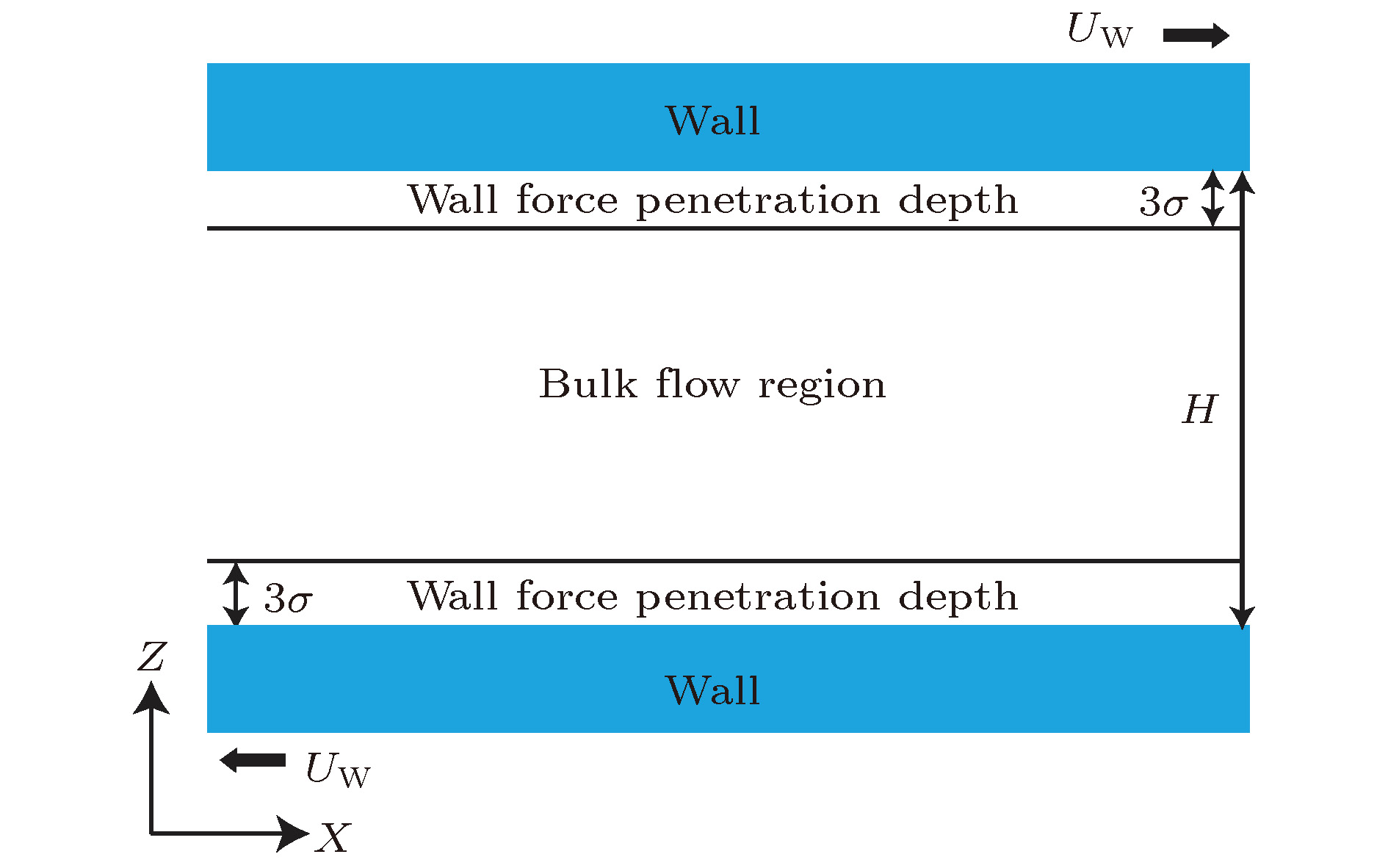
-
采用分子动力学方法研究了过渡区纳米通道内的壁面力场对气体剪切流动的影响规律. 在纳米尺度下, 壁面力场对流场的主导作用更加显著, 流动物理量对于壁面条件和系统温度的变化也更加敏感. 壁面原子的运动采用Einstein模型模拟, 结果表明随着壁面刚度的增加, 气体在近壁面区域的速度峰值减小, 气体分子与壁面的动量适应性变差. 壁面粗糙度通过金字塔形模型来研究, 发现无论是主流区域还是近壁区域, 壁面粗糙度对流动的影响都非常明显. 当粗糙单元高度增大时, 气体分子在壁面处的聚集现象明显, 与壁面完全动量适应. 本文还研究了系统温度对纳米通道流动的影响, 结果表明温度的影响是全局性的, 温度的升高导致整个通道内流速降低, 近壁区域气体密度减小, 气-固动量适应性变差.A three-dimensional non-equilibrium molecular dynamics method is adopted to investigate the influence of wall force field on the nanoscale gas flow in the transition regime. For the gas flow under nanoscale condition, the dominant effect of the wall force field on the flow field is more obvious, and the flow physical quantity is more sensitive to the change of the wall condition and system temperature. The motion of the wall atoms is governed by the Einstein theory, with using an elastic coefficient k to model the surface stiffness. The results indicate that the surface stiffness has little effect on the physical quantity distribution of the bulk flow region, but a certain influence on that of the near wall region. Increasing the value of the stiffness changes the velocity peak of the gas in the near-wall region and the tangential momentum adaptation coefficient (TMAC) towards lower values, thus demoting the momentum adaptability of the gas molecules to the surface. The wall roughness is simulated by a typical pyramidal model. It is found that the influence of wall roughness on the flow is very obvious, whether it is in the bulk flow region or in the near wall region. For the former case, the increase of roughness leads gas velocity and shear stress to increase, with density and normal stress remaining constant. The linear distribution of physical quantities is also affected to some extent. While for the latter case, as the roughness increases, the velocity of the fluid increases rapidly and approaches to the wall velocity. The peak of density increases, and the adsorption of gas molecules at the surface is obvious. The TMAC approaches to 1, suggesting that the gas and the surface achieve a complete momentum adaptation. Besides, the influence of system temperature on the gas flow in the nanochannel is also studied. The system temperature is controlled by the Nose-Hoover thermostat, making the flow field maintained at the target temperature through the damping coefficient. The results show that the effect of temperature is global in the whole flow region. The increase of temperature causes the flow velocity of the whole flow field to decrease, while the normal stress and shear stress to increase. A higher temperature leads to more frequent collisions between gas molecules, thus increasing the effective viscosity of the gas. At the same time, the degree of gas molecule adsorption in the near-wall region is reduced, contributing to a smaller TMAC value, and consequently a weaker gas-surface interaction.
-
Keywords:
- nanoscale gas flow /
- wall force effects /
- tangential momentum accommodation coefficient /
- shear stress
[1] Verbridge S S, Craighead H G, Parpia J M 2008 Appl. Phys. Lett. 92 013112
Google Scholar
[2] Cao B Y, Sun J, Chen M, Guo Z Y 2009 Int. J. Mol. Sci. 10 4638
Google Scholar
[3] Boettcher U, Li H, Callafon R A, Talke F E 2011 IEEE Trans. Magn. 47 1823
Google Scholar
[4] Song H Q, Yu M X, Zhu W Y, Zhang Y, Jiang S X 2013 Chin. Phys. Lett. 30 014701
Google Scholar
[5] Zhang W, Meng G, Wei X 2012 Microfluid. Nanofluid. 13 845
Google Scholar
[6] Maxwell J C 1879 Phil. Trans. R. Soc. Lond. 170 231
Google Scholar
[7] Sharipov F, Kalempa D 2004 Phys. Fluids 16 3779
Google Scholar
[8] Zhang Z Q, Zhang H W, Ye H F 2009 Appl. Phys. Lett. 95 154101
Google Scholar
[9] Zhang H W, Zhang Z Q, Zheng Y G, Ye H F 2010 Phys. Rev. E 81 066303
Google Scholar
[10] Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (Oxford: Oxford University Press) pp199−206
[11] Fan J, Shen C 2001 J. Comput. Phys. 167 393
Google Scholar
[12] Rapaport D C 2004 The Art of Molecular Dynamics Simulation (New York: Cambridge University Press) pp4, 5
[13] 曹炳阳, 陈民, 过增元 2006 55 5305
Google Scholar
Cao B Y, Chen M, Guo Z Y 2006 Acta Phys. Sin. 55 5305
Google Scholar
[14] Cao B Y 2007 Mol. Phys. 105 1403
Google Scholar
[15] Priezjev N V 2011 J. Chem. Phys. 135 204704
Google Scholar
[16] Sun J, Li Z X 2008 Mol. Phys. 106 2325
Google Scholar
[17] Spijker P, Markvoort A J, Nedea S V, Hilbers P A 2010 Phys. Rev. E 81 011203
Google Scholar
[18] Xie H, Liu C 2011 Mod. Phys. Lett. B 25 773
Google Scholar
[19] Kamali R, Kharazmi A 2011 Int. J. Therm. Sci. 50 226
Google Scholar
[20] Barisik M, Beskok A 2011 Microfluid. Nanofluid. 11 611
Google Scholar
[21] Barisik M, Beskok A 2012 Microfluid. Nanofluid. 13 789
Google Scholar
[22] Noorian H, Toghraie D, Azimian A R 2014 Heat Mass Transfer 50 105
Google Scholar
[23] Bao F B, Huang Y L, Qiu L M, Lin J Z 2015 Mol. Phys. 113 561
Google Scholar
[24] Bao F B, Huang Y L, Zhang Y H, Lin J Z 2015 Microfluid. Nanofluid. 18 1075
Google Scholar
[25] To Q D, Leonard C, Lauriat G 2015 Phys. Rev. E 91 023015
Google Scholar
[26] Liakopoulos A, Sofos F, Karakasidis T E 2016 Microfluid. Nanofluid. 20 24
Google Scholar
[27] Lim W W, Suaning G J, McKenzie D R 2016 Phys. Fluids 28 097101
Google Scholar
[28] 王胜, 徐进良, 张龙艳 2017 66 204704
Google Scholar
Wang S, Xu J L, Zhang L Y 2017 Acta Phys. Sin. 66 204704
Google Scholar
[29] 张冉, 谢文佳, 常青, 李桦 2018 67 084701
Google Scholar
Zhang R, Xie W J, Chang Q, Li H 2018 Acta Phys. Sin. 67 084701
Google Scholar
[30] Hook J R, Hall H E 1991 Solid State Physics (Chichester: Wiley) pp96−106
[31] Priezjev N V 2007 J. Chem. Phys. 127 144708
Google Scholar
[32] Asproulis N, Drikakis D 2010 Phys. Rev. E 81 061503
Google Scholar
[33] Asproulis N 2011 Phys. Rev. E 84 031504
Google Scholar
[34] Wu L, Bogy D B 2002 J. Tribol.-T. ASME 124 562
Google Scholar
[35] Cao B Y, Chen M, Guo Z Y 2005 Appl. Phys. Lett. 86 091905
Google Scholar
[36] Cieplak M, Koplik J, Banavar J R 2001 Phys. Rev. Lett. 86 803
Google Scholar
[37] 张冉, 常青, 李桦 2018 67 223401
Google Scholar
Zhang R, Chang Q, Li H 2018 Acta Phys. Sin. 67 223401
Google Scholar
[38] Evans D J, Hoover W G 1986 Annu. Rev. Fluid Mech. 18 243
Google Scholar
[39] Fukui S, Shimada H, Yamane K, Matsuoka H 2005 Microsyst. Technol. 11 805
Google Scholar
[40] Bahukudumbi P, Park J H, Beskok A 2003 Microscale Thermophy. Eng. 7 291
Google Scholar
-
图 3 粗糙纳米通道中的气体剪切流动示意图
Fig. 3. Schematics of the shear-driven gaseous flow in a rough channel.
图 4 不同壁面弹性系数条件下流场速度分布 (a)无量纲速度分布; (b)近壁面区域速度分布
Fig. 4. Velocity profiles with different surface stiffness: (a) Normalized velocity profiles; (b) near-wall velocity profiles.
图 5 不同壁面弹性系数条件下纳米通道中的密度分布
Fig. 5. Density distribution with different surface stiffness.
图 6 不同壁面弹性系数条件下纳米通道中的正应力分布
Fig. 6. Normal stress distribution with different surface stiffness.
图 7 不同壁面弹性系数条件下纳米通道中的剪切应力分布
Fig. 7. Shear stress distribution with different surface stiffness.
图 8 不同壁面粗糙度下的流场无量纲速度分布
Fig. 8. Normalized velocity profiles with different surface roughness.
图 9 不同壁面粗糙度下近壁区域流场无量纲速度分布
Fig. 9. Near-wall normalized velocity profiles with different surface roughness.
图 10 不同壁面粗糙度下近壁区域流场密度分布
Fig. 10. Near-wall density distribution with different surface roughness.
图 11 不同壁面粗糙度下近壁区域流场正应力分布
Fig. 11. Near-wall normal stress distribution with different surface roughness.
图 12 不同壁面粗糙度下近壁区域流场剪切应力分布
Fig. 12. Near-wall shear stress distribution with different surface roughness.
图 13 不同温度条件下的流场无量纲速度分布
Fig. 13. Normalized velocity profiles with different temperature conditions.
图 14 不同温度条件下近壁区域流场速度分布
Fig. 14. Near-wall velocity profiles with different temperature conditions.
图 15 不同温度条件下近壁区域流场密度分布
Fig. 15. Near-wall density distribution with different temperature conditions.
图 16 不同温度条件下近壁区域流场正应力分布
Fig. 16. Near-wall normal stress distribution with different temperature conditions.
图 17 不同温度条件下近壁区域流场剪切应力分布
Fig. 17. Near-wall normal stress distribution with different temperature conditions.
表 1 计算条件设置
Table 1. Parameters of the study on the influences of surface stiffness, roughness and temperature.
研究目的 $\rho /{\rm{kg}} \cdot {{\rm{m}}^{ - {\rm{3}}}}$ $H/{\rm{nm}}$ ${L_X}/{\rm{nm}}$ ${L_Y}/{\rm{nm}}$ 参数设置 弹性系数影响 1.86 10.89 65.38 65.38 $K/\varepsilon \cdot {\sigma ^{ - 2}}=300,\;500,\;800,\;1000,\;\infty $ 粗糙度影响 1.86 10.89 65.38 65.38 ${H_{{\rm{roughness}}}}=0.27, 0.54, 0.81\;{\rm{nm}}$ 温度影响 1.86 10.89 65.38 65.38 $T=248, 273, 298, 323, 348, 373\;{\rm{K}}$ 
下载: 导出CSV
表 2 不同壁面弹性系数条件下纳米通道中的剪切应力及TMAC大小
Table 2. Shear stress and TMAC values with different surface stiffness.
$K/\varepsilon \cdot {\sigma ^{ - 2}}$ ${\rho _{{\rm{Bulk}}}}/{\rm{kg}} \cdot {{\rm{m}}^{ - 3}}$ $\lambda /{\rm{nm}}$ $H/{\rm{nm}}$ $Kn$ ${\tau _{{\rm{Theo}},\sigma = 1.0}}/{\rm{kPa}}$ ${\tau _{{\rm{MD}}}}/{\rm{kPa}}$ TMAC 300 1.76 65.00 10.90 5.96 19.88 12.19 0.750 500 1.76 65.00 10.90 5.96 19.86 12.07 0.746 800 1.76 64.95 10.90 5.96 19.89 11.95 0.741 1000 1.76 64.98 10.90 5.96 19.88 11.96 0.741 $ \infty$ 1.76 64.72 10.90 5.96 19.95 11.75 0.736
下载: 导出CSV
表 3 不同温度条件下主流区域正应力与理论值对比
Table 3. Comparisons of normal stress with its theoretic values in bulk flow under different temperature conditions.
T/K ${{\rho }_{\rm{Bulk}}}/\rm{kg}\cdot {{\rm{m}}^{-{\rm{3}}}}$ ${s_{xx}}/{\rm{kPa}}$ ${s_{yy}}/{\rm{kPa}}$ ${s_{zz}}/{\rm{kPa}}$ ${P_{{\rm{MD}}}}/{\rm{kPa}}$ ${P_{{\rm{Theo}}}}/{\rm{kPa}}$ Error/% 248 1.69 87.97 84.88 87.11 86.65 87.00 0.40 273 1.73 98.99 95.38 97.89 97.56 98.26 0.71 298 1.76 109.54 106.01 108.97 108.48 109.41 0.85 323 1.80 120.26 116.97 119.68 118.72 120.93 1.83 348 1.82 130.32 127.12 129.69 128.99 131.79 2.13 373 1.83 140.44 137.23 140.28 139.43 142.43 2.11
下载: 导出CSV
-
[1] Verbridge S S, Craighead H G, Parpia J M 2008 Appl. Phys. Lett. 92 013112
Google Scholar
[2] Cao B Y, Sun J, Chen M, Guo Z Y 2009 Int. J. Mol. Sci. 10 4638
Google Scholar
[3] Boettcher U, Li H, Callafon R A, Talke F E 2011 IEEE Trans. Magn. 47 1823
Google Scholar
[4] Song H Q, Yu M X, Zhu W Y, Zhang Y, Jiang S X 2013 Chin. Phys. Lett. 30 014701
Google Scholar
[5] Zhang W, Meng G, Wei X 2012 Microfluid. Nanofluid. 13 845
Google Scholar
[6] Maxwell J C 1879 Phil. Trans. R. Soc. Lond. 170 231
Google Scholar
[7] Sharipov F, Kalempa D 2004 Phys. Fluids 16 3779
Google Scholar
[8] Zhang Z Q, Zhang H W, Ye H F 2009 Appl. Phys. Lett. 95 154101
Google Scholar
[9] Zhang H W, Zhang Z Q, Zheng Y G, Ye H F 2010 Phys. Rev. E 81 066303
Google Scholar
[10] Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (Oxford: Oxford University Press) pp199−206
[11] Fan J, Shen C 2001 J. Comput. Phys. 167 393
Google Scholar
[12] Rapaport D C 2004 The Art of Molecular Dynamics Simulation (New York: Cambridge University Press) pp4, 5
[13] 曹炳阳, 陈民, 过增元 2006 55 5305
Google Scholar
Cao B Y, Chen M, Guo Z Y 2006 Acta Phys. Sin. 55 5305
Google Scholar
[14] Cao B Y 2007 Mol. Phys. 105 1403
Google Scholar
[15] Priezjev N V 2011 J. Chem. Phys. 135 204704
Google Scholar
[16] Sun J, Li Z X 2008 Mol. Phys. 106 2325
Google Scholar
[17] Spijker P, Markvoort A J, Nedea S V, Hilbers P A 2010 Phys. Rev. E 81 011203
Google Scholar
[18] Xie H, Liu C 2011 Mod. Phys. Lett. B 25 773
Google Scholar
[19] Kamali R, Kharazmi A 2011 Int. J. Therm. Sci. 50 226
Google Scholar
[20] Barisik M, Beskok A 2011 Microfluid. Nanofluid. 11 611
Google Scholar
[21] Barisik M, Beskok A 2012 Microfluid. Nanofluid. 13 789
Google Scholar
[22] Noorian H, Toghraie D, Azimian A R 2014 Heat Mass Transfer 50 105
Google Scholar
[23] Bao F B, Huang Y L, Qiu L M, Lin J Z 2015 Mol. Phys. 113 561
Google Scholar
[24] Bao F B, Huang Y L, Zhang Y H, Lin J Z 2015 Microfluid. Nanofluid. 18 1075
Google Scholar
[25] To Q D, Leonard C, Lauriat G 2015 Phys. Rev. E 91 023015
Google Scholar
[26] Liakopoulos A, Sofos F, Karakasidis T E 2016 Microfluid. Nanofluid. 20 24
Google Scholar
[27] Lim W W, Suaning G J, McKenzie D R 2016 Phys. Fluids 28 097101
Google Scholar
[28] 王胜, 徐进良, 张龙艳 2017 66 204704
Google Scholar
Wang S, Xu J L, Zhang L Y 2017 Acta Phys. Sin. 66 204704
Google Scholar
[29] 张冉, 谢文佳, 常青, 李桦 2018 67 084701
Google Scholar
Zhang R, Xie W J, Chang Q, Li H 2018 Acta Phys. Sin. 67 084701
Google Scholar
[30] Hook J R, Hall H E 1991 Solid State Physics (Chichester: Wiley) pp96−106
[31] Priezjev N V 2007 J. Chem. Phys. 127 144708
Google Scholar
[32] Asproulis N, Drikakis D 2010 Phys. Rev. E 81 061503
Google Scholar
[33] Asproulis N 2011 Phys. Rev. E 84 031504
Google Scholar
[34] Wu L, Bogy D B 2002 J. Tribol.-T. ASME 124 562
Google Scholar
[35] Cao B Y, Chen M, Guo Z Y 2005 Appl. Phys. Lett. 86 091905
Google Scholar
[36] Cieplak M, Koplik J, Banavar J R 2001 Phys. Rev. Lett. 86 803
Google Scholar
[37] 张冉, 常青, 李桦 2018 67 223401
Google Scholar
Zhang R, Chang Q, Li H 2018 Acta Phys. Sin. 67 223401
Google Scholar
[38] Evans D J, Hoover W G 1986 Annu. Rev. Fluid Mech. 18 243
Google Scholar
[39] Fukui S, Shimada H, Yamane K, Matsuoka H 2005 Microsyst. Technol. 11 805
Google Scholar
[40] Bahukudumbi P, Park J H, Beskok A 2003 Microscale Thermophy. Eng. 7 291
Google Scholar
下载:
计量
- 文章访问数: 8827
- PDF下载量: 93
- 被引次数: 0
