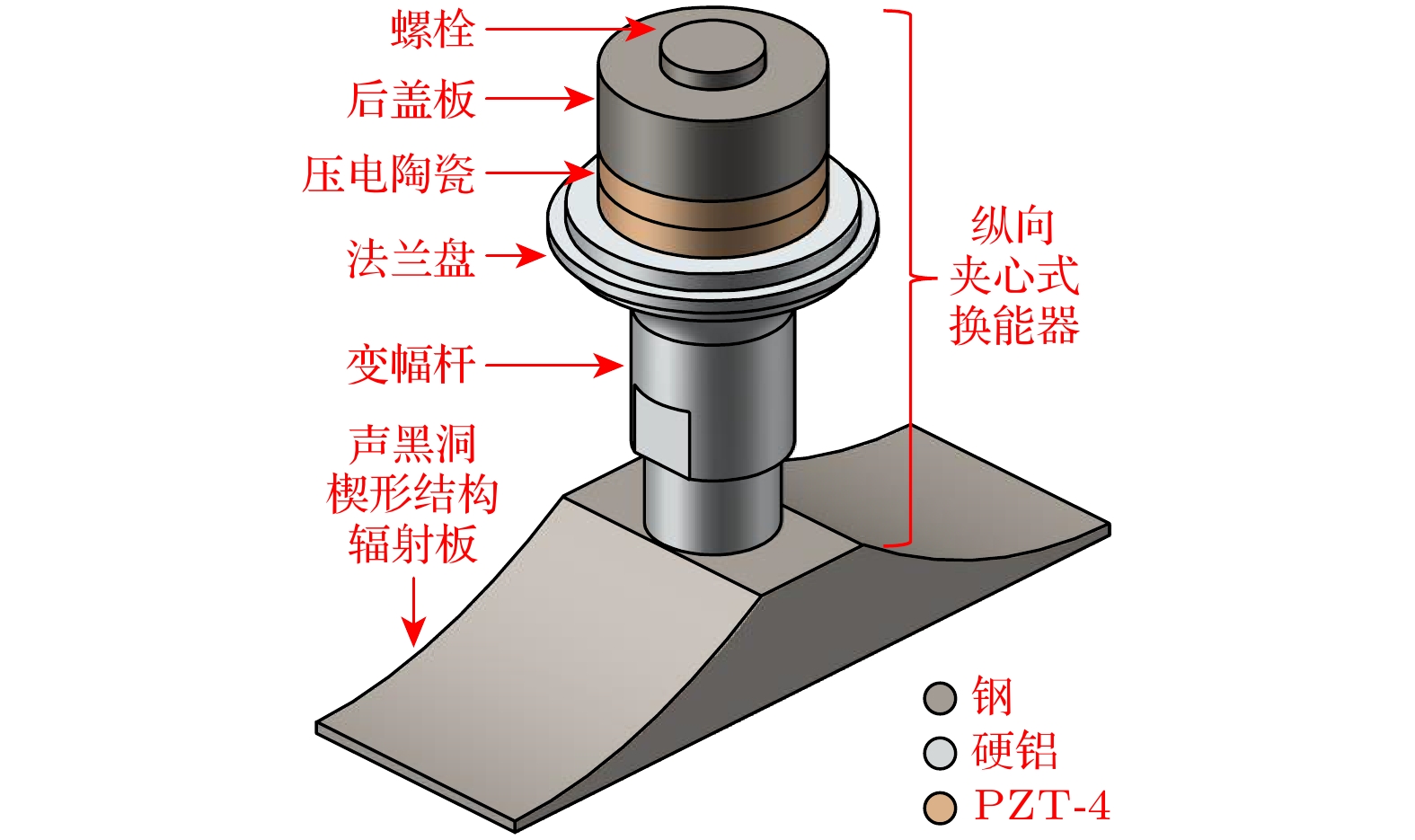
-
基于声黑洞结构独特的声波捕获与能量聚集效应, 提出了一种新型声黑洞楔形结构振动模式转换超声换能器. 该换能器由一个纵向夹心式换能器和一个声黑洞楔形结构辐射板组成. 基于铁木辛柯梁理论, 利用传输矩阵法建立了辐射板弯曲振动的理论模型, 计算得到的振动频率与有限元仿真频率吻合较好. 对换能器的电阻抗频率响应特性、振动模态以及空气中近场辐射声压分布进行了仿真模拟, 结果显示, 声黑洞楔形结构辐射板的振幅逐级增大, 近场辐射声压呈现出梯度分布的特点. 加工了换能器样机, 并对其进行实验测试, 测试结果验证了设计方法的可行性. 最后进行了超声悬浮实验, 结果表明声黑洞设计可以赋能于超声悬浮技术, 构造出声压梯度分布的声场, 实现粒子筛选.Acoustic black hole (ABH) structure has been extensively used in vibration mitigation, noise reduction, energy harvesting and so on, owing to its unique sound wave trapping and energy concentration effects. Besides, ABH structure holds emerging potential in improving the performance of ultrasonic device and constructing multifunctional acoustic field. Hence, an ultrasonic mode-conversion transducer consisting of a longitudinal sandwich transducer and an ABH wedge radiant plate is proposed in this work, in order to explore the potential applications of ABH in ultrasonic levitation and multifunctional particle manipulation. The theoretical model of flexural vibration of the radiant plate is established by utilizing Timoshenko beam theory and transfer matrix method, and the calculated vibration frequencies are in good agreement with those obtained by finite element method (FEM). The electrical impedance frequency response characteristics, vibration modes and the near-field sound pressure distribution of the transducer in air are also simulated. The results indicate that the amplitude of the ABH wedge radiant plate increases stepwise, and the sound pressure exhibits a gradient distribution. A prototype of the transducer is fabricated and experimentally tested, confirming the accuracy of FEM simulations and the feasibility of the design approach. Finally, the result of the ultrasonic levitation experiment indicates that the ABH design can give rise to gradient distribution of sound pressure in standing wave sound field for achieving precise particle sorting.
-
Keywords:
- acoustic black hole structure /
- air-coupled ultrasonic transducer /
- longitudinal-flexural mode conversion /
- ultrasonic levitation
[1] Krylov V V 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 1296
Google Scholar
[2] Bowyer E P, Krylov V V 2015 Appl. Acoust. 88 30
Google Scholar
[3] Chong B M P, Tan L B, Lim K M, Lee H P 2017 Int. J. Appl. Mech. 9 1750078
Google Scholar
[4] Zhao C, Prasad M G 2019 Acoustics 1 220
Google Scholar
[5] Krylov V V, Winward R 2007 J. Sound Vib. 300 43
Google Scholar
[6] Deng J, Guasch O, Maxit L, Gao N S 2022 J. Sound Vib. 526 19
Google Scholar
[7] Deng J, Gao N S, Chen X 2023 Thin Walled Struct. 184 6
Google Scholar
[8] Zhao L, Conlon S C, Semperlotti F 2015 Smart Mater. Struct. 24 065039
Google Scholar
[9] Liang Y K, Ji H L, Qiu J H, Cheng L, Wu Y P, Zhang C 2018 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM) Auckland, New Zealand, July 9–12, 2018 pp1372–1377
[10] Li H, Doaré O, Touzé C, Pelat A, Gautier F 2022 Int. J. Solids Struct. 238 111409
Google Scholar
[11] Zhang L, Kerschen G, Cheng L 2022 Mech. Syst. Signal Process. 177 109244
Google Scholar
[12] Zhang L, Tang X, Qin Z, Chu F 2022 Appl. Phys. Lett. 121 013902
Google Scholar
[13] Remillieux M C, Anderson B E, Le Bas P Y, Ulrich T J 2014 Ultrasonics 54 1409
Google Scholar
[14] Anderson B E, Remillieux M C, Le Bas P Y, Ulrich T J, Pieczonka L 2015 Ultrasonics 63 141
Google Scholar
[15] 刘洋, 陈诚, 林书玉 2024 73 084302
Google Scholar
Liu Y, Chen C, Lin S Y 2024 Acta Phys. Sin. 73 084302
Google Scholar
[16] Chen C, Liu Y, Wang C H, Guo J Z, Lin S Y 2024 Ultrason. Sonochem. 111 107106
Google Scholar
[17] Zhan L P, Hua T Z, Chun Y K, Naquin T D, Jing H N, Yu H H, Yan C J, Xia M Q, Bachman H, Ran Z P, Hong X X, Hui H J, Huang T J 2022 Sci. Adv. 8 eabm2592
Google Scholar
[18] Yin Q, Yong S H, Long W Z, Chao M Z, Ming Z W 2024 Microsyst. Nanoeng. 10 144
Google Scholar
[19] 林书玉, 张福成, 郭孝武, 董胜林 1995 陕西师范大学学报(自然科学版) 23 43
Lin S Y, Zhang F C, Guo X W, Dong S L 1995 J. Shaanxi Normal Univ. (Nat. Sci. Ed.) 23 43
[20] 林书玉 2004 超声换能器的原理及设计 (北京: 科学出版社) 第91—111页
Lin S Y 2004 The Theory and Design of Ultrasonic Transducers (Beijing: Science Press) pp91–111
[21] Williams F W, Banerjee J R 1985 J. Sound Vib. 99 121
Google Scholar
[22] Miklowitz J 2021 J. Appl. Mech. 20 511
Google Scholar
[23] Mori E 1989 Ultrasonics International 89 Conference Proceedings Madrid, Spain, July 3–7, 1989 p256
[24] Zhou G, Li M 2000 J. Acoust. Soc. Am. 107 1358
Google Scholar
-
图 1 声黑洞楔形结构振动模式转换超声换能器
Fig. 1. Ultrasonic transducer with acoustic black hole wedge structure based on vibration mode-conversion.
图 2 换能器尺寸参数示意图 (a)纵向夹心式换能器; (b)声黑洞楔形结构辐射板
Fig. 2. Schematic diagram of the transducer’s dimensions: (a) The longitudinal sandwich transducer; (b) the ABH wedge radiant plate.
图 7 有限元仿真得到的换能器电阻抗频率响应曲线
Fig. 7. Electrical impedance frequency response curve of the transducer obtained by FEM.
图 8 (a)换能器整体模态; (b)辐射板弯曲振动模态
Fig. 8. (a) Vibration mode of the whole transducer; (b) the flexural vibration mode of the radiant plate.
图 9 归一化的辐射板横向位移分布曲线
Fig. 9. Curve of normalized transverse displacement distribution of the radiant plate.
图 10 空气中辐射近声场建模的网格划分
Fig. 10. Meshing of the modeling of radiated near sound field in air.
图 11 空气中近场声压分布有限元仿真结果
Fig. 11. Near-field sound pressure distribution in air obtained by FEM.
图 12 声黑洞楔形结构振动模式转换换能器样机
Fig. 12. Prototype of the ultrasonic transducer with acoustic black hole wedge structure based on vibration mode-conversion.
图 13 阻抗分析实验 (a) WK6500B精密阻抗分析仪及换能器样机; (b)换能器输入电阻抗及相位的频率响应曲线
Fig. 13. Impedance analysis experiment: (a) The WK6500B precision impedance analyzer and the transducer prototype; (b) frequency response curve of the input electric impedance and phase of the transducer.
图 14 激光测振实验 (a) Polytec PSV-400全场扫描式激光振动测量系统及换能器样机; (b)辐射板弯曲振动模态
Fig. 14. Laser vibrometry experiment: (a) The Polytec PSV-400 full-field scanning laser vibrometry system and the transducer prototype; (b) flexural vibration mode of the radiant plate.
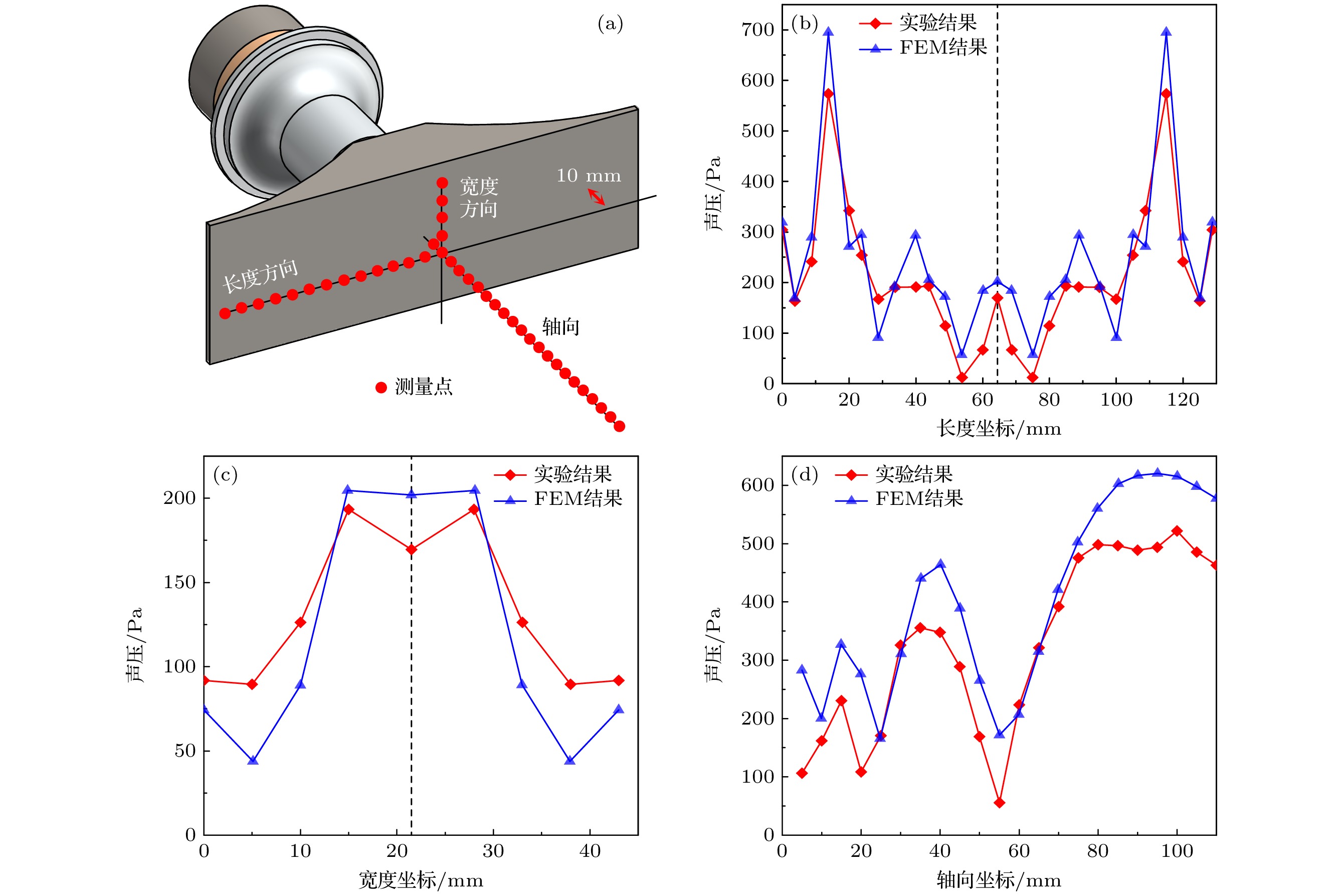
图 16 空气中近场声压分布实验测量与有限元仿真结果对比 (a)测量点示意; (b)距辐射面10 mm处长度方向上声压分布; (c)距辐射面10 mm处宽度方向上声压分布; (d)轴向上声压分布
Fig. 16. Comparison of the experimental and FEM’s results of near-field sound pressure distribution in air: (a) Schematic diagram of measuring points; (b) sound pressure distribution in the length direction 10 mm away from the radiant surface; (c) sound pressure distribution in the width direction 10 mm away from the radiant surface; (d) axial sound pressure distribution.
图 17 (a)超声悬浮实验平台; (b) EPS小球的梯度悬浮
Fig. 17. (a) Platform of ultrasonic levitation experiment; (b) gradient levitation of EPS pellets.
表 1 辐射板弯曲振动频率计算结果对比
Table 1. Comparison of calculated flexural vibration frequency of the radiant plate.
参数 一阶 二阶 三阶 四阶 五阶 六阶 ${f_{\text{T}}}$/Hz 5575 13909 26722 43370 62585 83304 ${f_{\text{F}}}$/Hz 5431 13402 26101 43287 62847 83737 ${\varDelta _1}$/% 2.65 3.78 2.38 0.19 0.42 0.52 
下载: 导出CSV
-
[1] Krylov V V 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 1296
Google Scholar
[2] Bowyer E P, Krylov V V 2015 Appl. Acoust. 88 30
Google Scholar
[3] Chong B M P, Tan L B, Lim K M, Lee H P 2017 Int. J. Appl. Mech. 9 1750078
Google Scholar
[4] Zhao C, Prasad M G 2019 Acoustics 1 220
Google Scholar
[5] Krylov V V, Winward R 2007 J. Sound Vib. 300 43
Google Scholar
[6] Deng J, Guasch O, Maxit L, Gao N S 2022 J. Sound Vib. 526 19
Google Scholar
[7] Deng J, Gao N S, Chen X 2023 Thin Walled Struct. 184 6
Google Scholar
[8] Zhao L, Conlon S C, Semperlotti F 2015 Smart Mater. Struct. 24 065039
Google Scholar
[9] Liang Y K, Ji H L, Qiu J H, Cheng L, Wu Y P, Zhang C 2018 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM) Auckland, New Zealand, July 9–12, 2018 pp1372–1377
[10] Li H, Doaré O, Touzé C, Pelat A, Gautier F 2022 Int. J. Solids Struct. 238 111409
Google Scholar
[11] Zhang L, Kerschen G, Cheng L 2022 Mech. Syst. Signal Process. 177 109244
Google Scholar
[12] Zhang L, Tang X, Qin Z, Chu F 2022 Appl. Phys. Lett. 121 013902
Google Scholar
[13] Remillieux M C, Anderson B E, Le Bas P Y, Ulrich T J 2014 Ultrasonics 54 1409
Google Scholar
[14] Anderson B E, Remillieux M C, Le Bas P Y, Ulrich T J, Pieczonka L 2015 Ultrasonics 63 141
Google Scholar
[15] 刘洋, 陈诚, 林书玉 2024 73 084302
Google Scholar
Liu Y, Chen C, Lin S Y 2024 Acta Phys. Sin. 73 084302
Google Scholar
[16] Chen C, Liu Y, Wang C H, Guo J Z, Lin S Y 2024 Ultrason. Sonochem. 111 107106
Google Scholar
[17] Zhan L P, Hua T Z, Chun Y K, Naquin T D, Jing H N, Yu H H, Yan C J, Xia M Q, Bachman H, Ran Z P, Hong X X, Hui H J, Huang T J 2022 Sci. Adv. 8 eabm2592
Google Scholar
[18] Yin Q, Yong S H, Long W Z, Chao M Z, Ming Z W 2024 Microsyst. Nanoeng. 10 144
Google Scholar
[19] 林书玉, 张福成, 郭孝武, 董胜林 1995 陕西师范大学学报(自然科学版) 23 43
Lin S Y, Zhang F C, Guo X W, Dong S L 1995 J. Shaanxi Normal Univ. (Nat. Sci. Ed.) 23 43
[20] 林书玉 2004 超声换能器的原理及设计 (北京: 科学出版社) 第91—111页
Lin S Y 2004 The Theory and Design of Ultrasonic Transducers (Beijing: Science Press) pp91–111
[21] Williams F W, Banerjee J R 1985 J. Sound Vib. 99 121
Google Scholar
[22] Miklowitz J 2021 J. Appl. Mech. 20 511
Google Scholar
[23] Mori E 1989 Ultrasonics International 89 Conference Proceedings Madrid, Spain, July 3–7, 1989 p256
[24] Zhou G, Li M 2000 J. Acoust. Soc. Am. 107 1358
Google Scholar
下载:
计量
- 文章访问数: 664
- PDF下载量: 10
- 被引次数: 0
