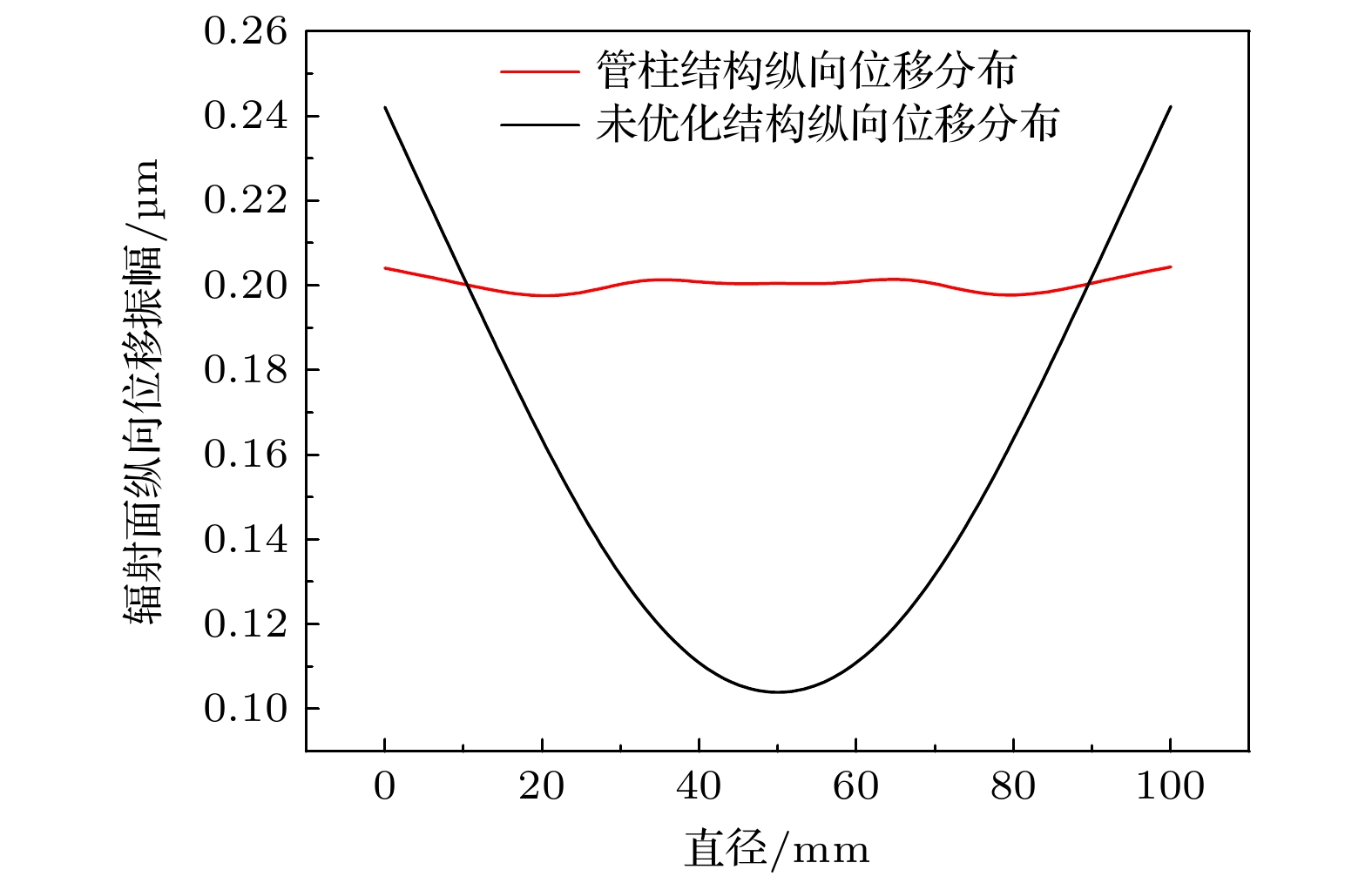
-
大尺寸压电超声换能器的耦合振动会导致其辐射面纵向位移振幅的平均值较小, 振幅分布不均匀, 严重影响系统的性能和可靠性. 为了改善大尺寸超声振动系统性能, 可利用二维孔/槽型近周期声子晶体结构对横向振动进行抑制, 但在对横向振动抑制的同时, 该结构会对换能器机械强度和工作带宽等性能参数造成不利的影响. 针对这一问题, 本文提出利用管柱型近周期声子晶体点缺陷结构对大尺寸夹心式纵振压电陶瓷换能器进行优化的新思路. 该方法不仅可以利用构造的固/气二维近周期声子晶体结构的点缺陷模式, 获得极低的能量损耗, 有效提高系统辐射面的纵向位移振幅和振幅分布均匀度; 也可以利用管柱结构中的双环形孔增强声波的多重散射, 使得换能器在管柱柱高较低的条件下产生禁带, 在有效抑制横向振动的同时, 大幅拓宽换能器系统的工作带宽, 增强系统的稳定性和机械强度, 降低加工成本. 仿真结果证明了优化的有效性.
-
关键词:
- 横向振动 /
- 大尺寸压电超声换能器性能 /
- 管柱型近周期声子晶体点缺陷结构
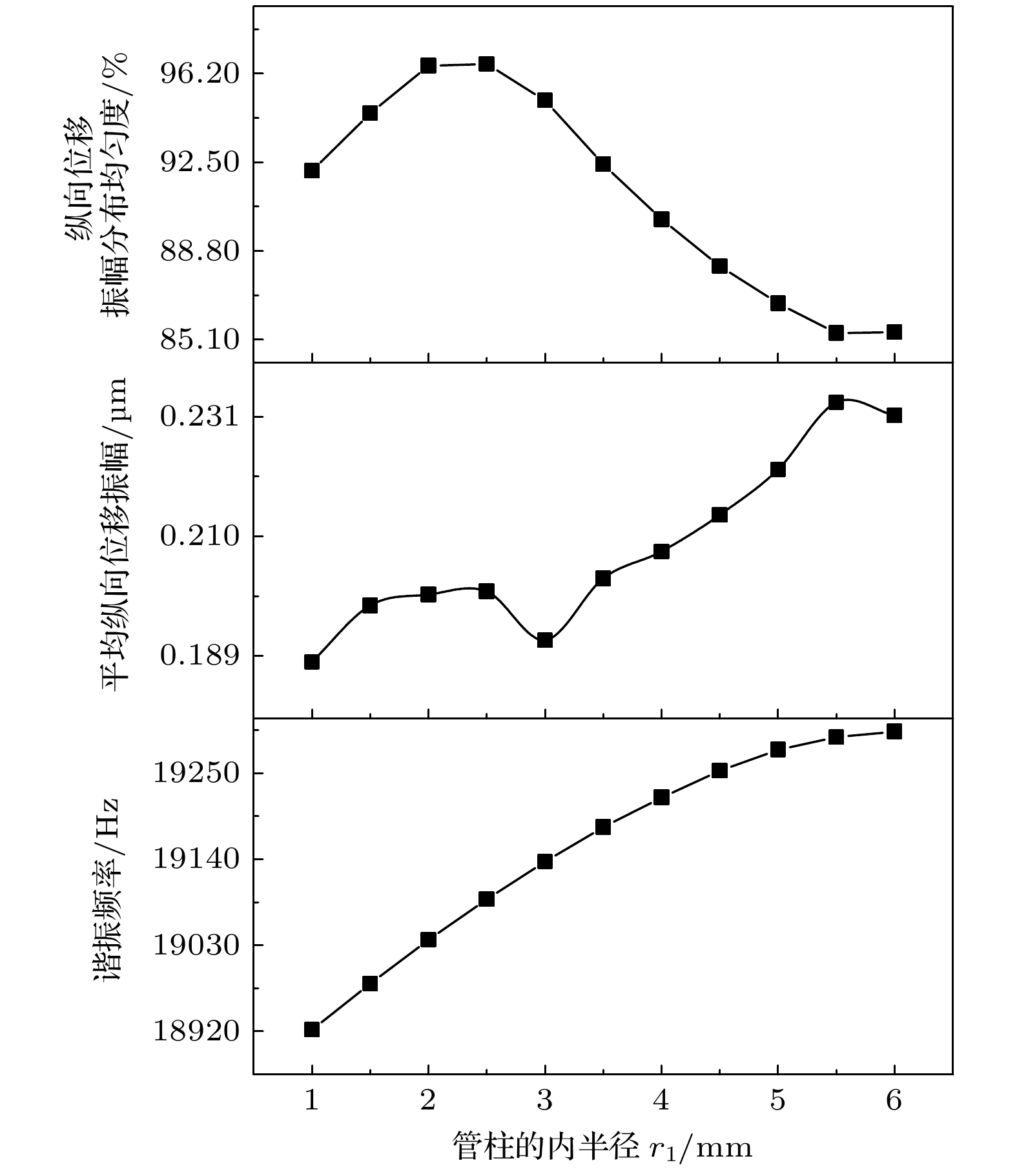
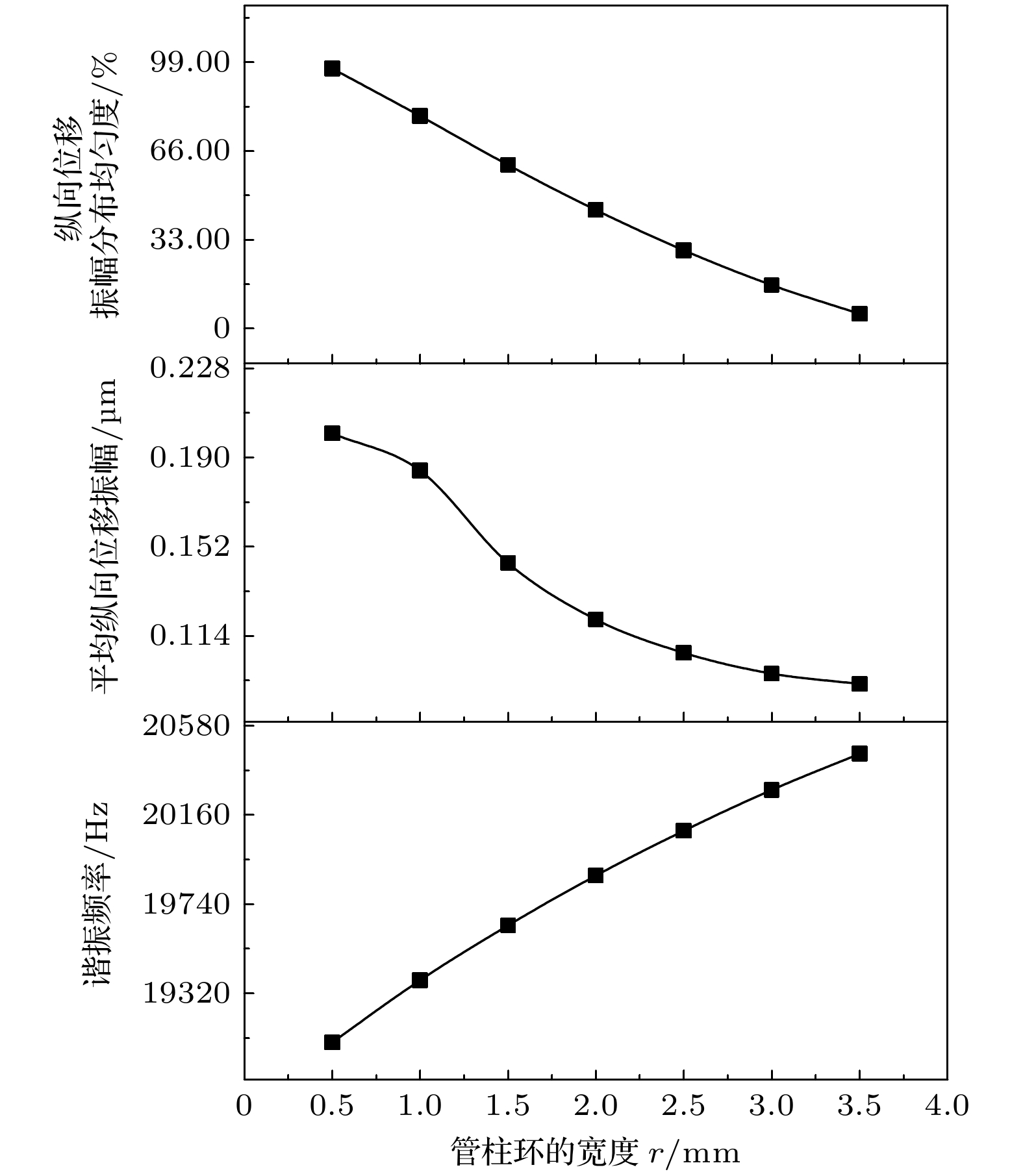
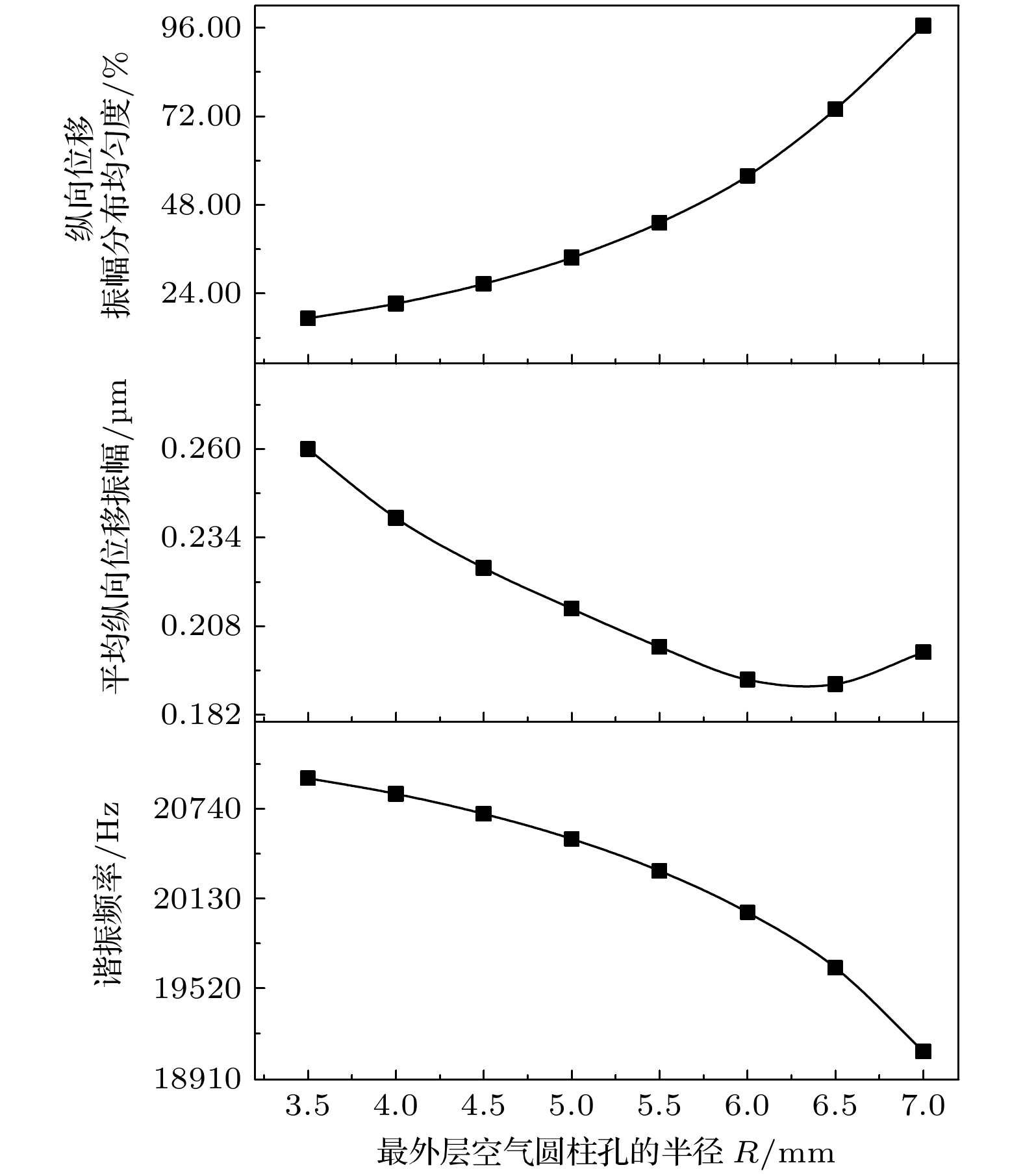
The coupling vibration of large-scale piezoelectric ultrasonic transducer will make the average value of the longitudinal displacement amplitude of its radiation surface small and the amplitude distribution uneven, which seriously affects the performance and reliability of the system. In order to improve the performance of large-scale ultrasonic vibration system, a two-dimensional hole/slot near-periodic phononic crystal structure is used to suppress the transverse vibration, but the structure will in turn affect the mechanical strength of the transducer while achieving the suppression of the transverse vibration. The working bandwidth and other performance parameters have adverse effects. Based on this, a new idea of optimizing the large-scale sandwich longitudinal vibration piezoelectric ceramic transducer by using the tubular near-periodic phononic crystal point defect structure is proposed. This method can not only use the point defect mode of the constructed solid/gas two-dimensional near-periodic phononic crystal structure to obtain extremely low energy loss, but also effectively improve the longitudinal displacement amplitude and amplitude distribution uniformity of the radiation surface of the system. The double annular holes in the pipe string structure can also be used to enhance the multiple scattering of sound waves, so that the transducer can also produce a band gap under the low conditions of the pipe string, effectively suppressing the transverse vibration, at the same time, significantly broadening the working bandwidth of the transducer system, enhancing the stability and mechanical strength of the system, and reducing the processing cost. Simulation results and experimental processing test results also prove the effectiveness of the optimization. In order to find the best parameters for the performance of the large-scale longitudinal vibration piezoelectric ultrasonic transducer, in the paper the finite element analysis software is used to study the influence of the inner radius r1 of the pipe string, the width r of the pipe string ring, the radius R of the outermost air cylinder hole, and the height h2 of the pipe string at the longitudinal resonance frequency of the transducer performance, the longitudinal displacement amplitude distribution uniformity of the radiation surface, and the average longitudinal displacement amplitude. In the research is finally found the range of parameters that can make the performance of the transducer reach a relatively ideal state. The simulation results show that the tubular near-periodic phononic crystal point defect structure can improve the performance of large-scale longitudinal vibration piezoelectric ultrasonic transducer. -
Keywords:
- transverse vibration /
- performance of large-scale piezoelectric ultrasonic transducer /
- tubular near-periodic phononic crystal point defect structure
[1] 刘晓晗, 黄大鸣, 王兴军, 张春红, 朱海军, 蒋最敏, 王迅 1997 46 200
Google Scholar
Liu X H, Huang D M, Wang X J, Zhang C H, Zhu H J, Jiang Z M, Wang X 1997 Acta Phys. Sin. 46 200
Google Scholar
[2] Sigalas M M, Economou E N 1992 J. Sound Vib. 158 377
Google Scholar
[3] Kushwaha M S, Halevi P, Dobrzynski L, Djafari-Rouhani B 1993 Phys. Rev. Lett. 71 2022
Google Scholar
[4] Adibi A, Lee R K 2002 Elec. Lett. 36 1376
Google Scholar
[5] Wang Y F, Wang Y S 2013 J. Vib. Acoust. 135 041009
Google Scholar
[6] Das S, Dwivedi K, Rajasekharan S G, Rao Y 2021 J. Vib. Control 27 827
Google Scholar
[7] Yang S, Yu W D, Pan N 2011 Physica B 406 963
Google Scholar
[8] Hsu J C, Wu T T 2006 Phys. Rev. B 74 144303
Google Scholar
[9] Khelif A, Aoubiza B, Mohammadi S, Adibi A, Laude V 2006 Phys. Rev. E 74 046610
Google Scholar
[10] Benchabane S, Gaiffe O, Salut R, Ulliac G, Laude V, Kokkonen K 2015 Appl. Phys. Lett. 106 081903
Google Scholar
[11] Ma T X, Fan Q S, Zhang C, Wang Y S 2021 J. Appl. Phys. 129 145104
Google Scholar
[12] Wu F, Hou Z, Liu Z, Liu Y 2001 Phys. Lett. A 292 198
Google Scholar
[13] Miyashita T 2014 Jpn. J. Appl. Phys. 45 4440
Google Scholar
[14] Li F, Liu J, Wu Y H 2011 J. Appl. Phys. 109 124907
Google Scholar
[15] Li Y G, Chen T N, Wang X, Ma T, Ping J 2014 J. Appl. Phys. 116 0249041
Google Scholar
[16] Lin S 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 1990
Google Scholar
[17] Lin S 1995 Appl. Acoust. 44 249
Google Scholar
[18] Ren S C 1983 Acta Acust. 1 152
Google Scholar
[19] Rani M R, Prakasan K, Rudramoorthy R 2014 Inter. J. Desi. Eng. 5 344
Google Scholar
[20] Adachi K, Ueha S 1990 J. Acoust. Soc. Am. 87 208
Google Scholar
[21] 王莎, 林书玉 2019 68 024303
Google Scholar
Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303
Google Scholar
[22] Wang S, Lin S 2019 Ultra. 99 105954
Google Scholar
[23] 赵甜甜, 林书玉, 段祎林 2018 67 224207
Google Scholar
Zhao T T, Lin S Y, Duan Y L 2018 Acta Phys. Sin. 67 224207
Google Scholar
[24] Zhao T T, Lin S Y 2019 Acta Acust. United Acust. 105 953
Google Scholar
[25] 王莎, 林书玉, 段祎林 2018 应用声学 37 811
Google Scholar
Wang S, Lin S Y, Duan Y L 2018 Appl. Acoust. 37 811
Google Scholar
[26] Hu L Q, Wang S, Lin S Y 2022 Chin. Phys. B 31 054302
Google Scholar
[27] 林基艳, 林书玉 2022 陕西师范大学学报(自然科学版) 50 117
Google Scholar
Lin J Y, Lin S Y 2022 J. Shaanxi Norm. Uni. (Natural Science Edition) 50 117
Google Scholar
[28] 胡理情, 林书玉 2021 应用声学 40 323
Google Scholar
Hu L Q, Lin S Y 2021 Appl. Acoust. 40 323
Google Scholar
[29] Lin J Y, Lin S Y 2020 Cryst. 10 21
Google Scholar
[30] 林基艳, 林书玉, 王升, 李耀 2021 中国科学: 物理学 力学 天文学 51 094311
Google Scholar
Lin J Y, Lin S Y, Wang S, Li Y 2021 Sci. Sin. Phys. Mech. Astron. 51 094311
Google Scholar
[31] 魏琦, 程营, 刘晓峻 2011 60 124301
Google Scholar
Wei Q, Cheng Y, Liu X J 2011 Acta Phys. Sin. 60 124301
Google Scholar
[32] Mohammadi S, Eftekhar A. A, Khelif A, Hunt W D, Adibi A 2008 Appl. Phys. Lett. 92 221905
Google Scholar
[33] Wu T T, Huang Z G, Tsai T C, Wu T C 2008 Appl. Phys. Lett. 93 111902
Google Scholar
[34] Pennec Y, Djafari-Rouhani B, Larabi H, Vasseur J O, Hladky-Hennion A C 2008 Phys. Rev. B 78 104105
Google Scholar
[35] Pourabolghasem R, Khelif A, Mohammadi S, Eftekhar A A, Adibi A A 2014 J. Appl. Phys. 116 013514
Google Scholar
[36] 舒风风 2016 博士学位论文 (长春: 中国科学院长春光学精密机械与物理研究所)
Shu F F 2016 Ph. D. Dissertation (Changchun: Changchun Institute of Optics, Precision Mechanics and Physics, Chinese Academy of Sciences) (in Chinese)
-
图 1 大尺寸夹心式纵振压电陶瓷超声换能器的结构(a)和振型图(b)
Fig. 1. (a) Structure and (b) vibration mode diagram of large-dimension sandwich longitudinal vibration piezoelectric ceramic ultrasonic transducer.
图 3 管柱型近周期声子晶体结构几何模型
Fig. 3. Geometric model of tubular near-periodic phononic crystal structure.
图 4 管柱型近周期声子晶体点缺陷结构的几何模型
Fig. 4. Geometric model of point defect structure in tubular near-periodic phononic crystals.
图 5 管柱型近周期声子晶体点缺陷结构的大尺寸压电超声换能器的前盖板
Fig. 5. Front cover plate of large-dimension piezoelectric ultrasonic transducer with tubular near-periodic phononic crystal point defect structure.
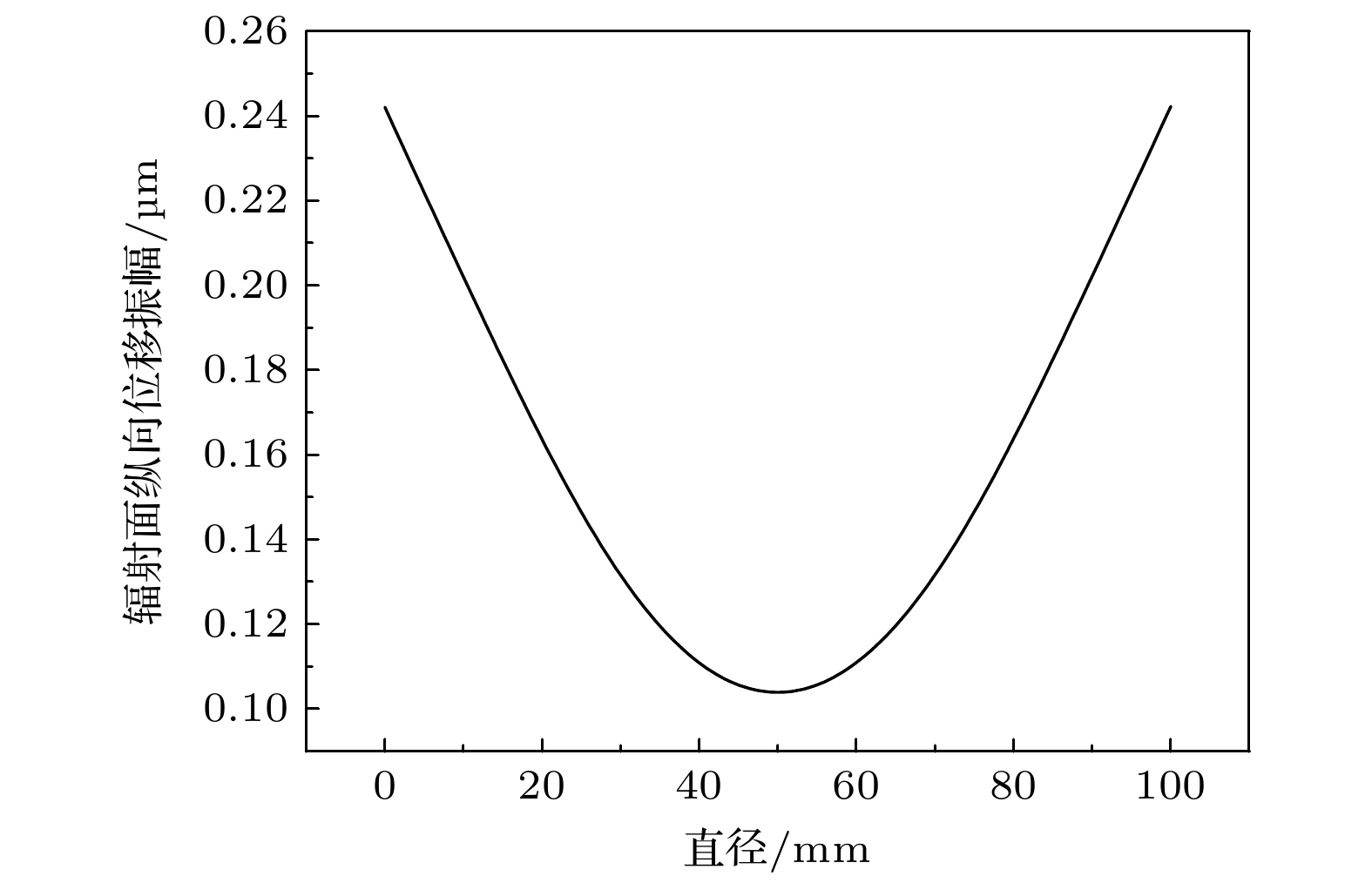
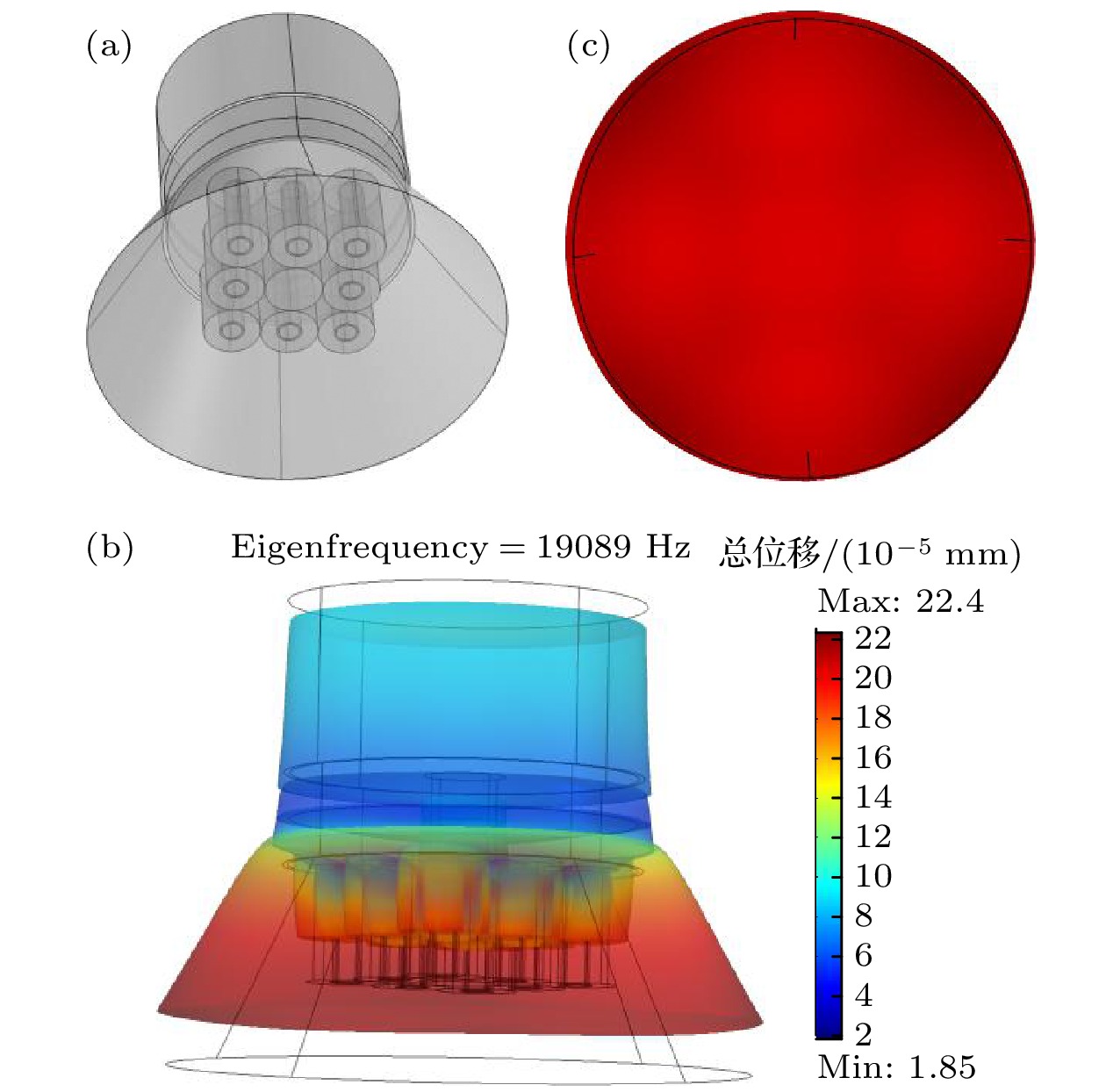
图 7 管柱型近周期声子晶体点缺陷结构的大尺寸压电超声换能器的(a)结构示意图、(b)振型图及(c)辐射面位移分布云图
Fig. 7. (a) Structure schematic, (b) vibration modal diagram, and (c) cloud diagram of displacement distribution of radiation surface of large-scale piezoelectric ultrasonic transducers with tubular near-period phononic crystal point defect structure.
图 8 辐射面纵向位移振幅分布对比图
Fig. 8. Comparison diagram of longitudinal displacement amplitude distribution of radiation surface.
图 10 管柱和无管柱结构的发射电压响应曲线
Fig. 10. Emission voltage response curves of tubular and non- tubular structures.
图 11 r1对换能器性能的影响
Fig. 11. Influence of the number of r1 on the performance of the transducer.
图 12 r对换能器性能的影响
Fig. 12. Influence of the number of r on the performance of the transducer.
图 13 R对换能器性能的影响
Fig. 13. Influence of the number of R on the performance of the transducer.
图 14 h2对换能器性能的影响
Fig. 14. Influence of the number of h2 on the performance of the transducer.
表 1 换能器的结构尺寸和材料属性参数
Table 1. Structural size and material property parameters of the transducer.
部件 材料属性 形状 外/大端半径/mm 内/小端半径/mm 高度/mm 前盖板 Aluminum 6063-T83 圆锥 50 31 35 压电陶瓷片(两片) PZT-4 等截面圆环 30 7 8 后盖板 Steel AISI 4340 等截面圆柱 31 31 30 
下载: 导出CSV
-
[1] 刘晓晗, 黄大鸣, 王兴军, 张春红, 朱海军, 蒋最敏, 王迅 1997 46 200
Google Scholar
Liu X H, Huang D M, Wang X J, Zhang C H, Zhu H J, Jiang Z M, Wang X 1997 Acta Phys. Sin. 46 200
Google Scholar
[2] Sigalas M M, Economou E N 1992 J. Sound Vib. 158 377
Google Scholar
[3] Kushwaha M S, Halevi P, Dobrzynski L, Djafari-Rouhani B 1993 Phys. Rev. Lett. 71 2022
Google Scholar
[4] Adibi A, Lee R K 2002 Elec. Lett. 36 1376
Google Scholar
[5] Wang Y F, Wang Y S 2013 J. Vib. Acoust. 135 041009
Google Scholar
[6] Das S, Dwivedi K, Rajasekharan S G, Rao Y 2021 J. Vib. Control 27 827
Google Scholar
[7] Yang S, Yu W D, Pan N 2011 Physica B 406 963
Google Scholar
[8] Hsu J C, Wu T T 2006 Phys. Rev. B 74 144303
Google Scholar
[9] Khelif A, Aoubiza B, Mohammadi S, Adibi A, Laude V 2006 Phys. Rev. E 74 046610
Google Scholar
[10] Benchabane S, Gaiffe O, Salut R, Ulliac G, Laude V, Kokkonen K 2015 Appl. Phys. Lett. 106 081903
Google Scholar
[11] Ma T X, Fan Q S, Zhang C, Wang Y S 2021 J. Appl. Phys. 129 145104
Google Scholar
[12] Wu F, Hou Z, Liu Z, Liu Y 2001 Phys. Lett. A 292 198
Google Scholar
[13] Miyashita T 2014 Jpn. J. Appl. Phys. 45 4440
Google Scholar
[14] Li F, Liu J, Wu Y H 2011 J. Appl. Phys. 109 124907
Google Scholar
[15] Li Y G, Chen T N, Wang X, Ma T, Ping J 2014 J. Appl. Phys. 116 0249041
Google Scholar
[16] Lin S 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 1990
Google Scholar
[17] Lin S 1995 Appl. Acoust. 44 249
Google Scholar
[18] Ren S C 1983 Acta Acust. 1 152
Google Scholar
[19] Rani M R, Prakasan K, Rudramoorthy R 2014 Inter. J. Desi. Eng. 5 344
Google Scholar
[20] Adachi K, Ueha S 1990 J. Acoust. Soc. Am. 87 208
Google Scholar
[21] 王莎, 林书玉 2019 68 024303
Google Scholar
Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303
Google Scholar
[22] Wang S, Lin S 2019 Ultra. 99 105954
Google Scholar
[23] 赵甜甜, 林书玉, 段祎林 2018 67 224207
Google Scholar
Zhao T T, Lin S Y, Duan Y L 2018 Acta Phys. Sin. 67 224207
Google Scholar
[24] Zhao T T, Lin S Y 2019 Acta Acust. United Acust. 105 953
Google Scholar
[25] 王莎, 林书玉, 段祎林 2018 应用声学 37 811
Google Scholar
Wang S, Lin S Y, Duan Y L 2018 Appl. Acoust. 37 811
Google Scholar
[26] Hu L Q, Wang S, Lin S Y 2022 Chin. Phys. B 31 054302
Google Scholar
[27] 林基艳, 林书玉 2022 陕西师范大学学报(自然科学版) 50 117
Google Scholar
Lin J Y, Lin S Y 2022 J. Shaanxi Norm. Uni. (Natural Science Edition) 50 117
Google Scholar
[28] 胡理情, 林书玉 2021 应用声学 40 323
Google Scholar
Hu L Q, Lin S Y 2021 Appl. Acoust. 40 323
Google Scholar
[29] Lin J Y, Lin S Y 2020 Cryst. 10 21
Google Scholar
[30] 林基艳, 林书玉, 王升, 李耀 2021 中国科学: 物理学 力学 天文学 51 094311
Google Scholar
Lin J Y, Lin S Y, Wang S, Li Y 2021 Sci. Sin. Phys. Mech. Astron. 51 094311
Google Scholar
[31] 魏琦, 程营, 刘晓峻 2011 60 124301
Google Scholar
Wei Q, Cheng Y, Liu X J 2011 Acta Phys. Sin. 60 124301
Google Scholar
[32] Mohammadi S, Eftekhar A. A, Khelif A, Hunt W D, Adibi A 2008 Appl. Phys. Lett. 92 221905
Google Scholar
[33] Wu T T, Huang Z G, Tsai T C, Wu T C 2008 Appl. Phys. Lett. 93 111902
Google Scholar
[34] Pennec Y, Djafari-Rouhani B, Larabi H, Vasseur J O, Hladky-Hennion A C 2008 Phys. Rev. B 78 104105
Google Scholar
[35] Pourabolghasem R, Khelif A, Mohammadi S, Eftekhar A A, Adibi A A 2014 J. Appl. Phys. 116 013514
Google Scholar
[36] 舒风风 2016 博士学位论文 (长春: 中国科学院长春光学精密机械与物理研究所)
Shu F F 2016 Ph. D. Dissertation (Changchun: Changchun Institute of Optics, Precision Mechanics and Physics, Chinese Academy of Sciences) (in Chinese)
下载:
计量
- 文章访问数: 2846
- PDF下载量: 105
- 被引次数: 0
