-
在使用高强度聚焦超声进行肋下病灶治疗的过程中, 肋骨的遮挡显著影响了治疗的效果, 在先前的研究中, 肋骨通常被视作完美吸声体, 这一模型虽然能够在一定程度上体现肋骨造成的影响, 但也同样可能导致对肋后能量的低估. 为弥补现有工作的不足, 本文提出了一种将肋骨视作强吸声体、而非完美吸声体的数值计算方法, 并使用ABS塑料构建的仿肋模型进行了相关实验以比较两类方法的优劣, 此外本文还在多层介质模型中研究了肋骨对非线性声场造成的影响. 由于肋骨在新模型中具有较大的声衰减系数, 现有算法在计算过程中容易出现数值振荡问题, 为此本研究使用了算子分离法以提高数值计算的稳定性, 并进一步通过矩阵向量化方法在后向隐式差分格式下实现了声场的稳定求解. 这些改进不仅提高了数值计算的准确性, 还揭示了完美吸声体模型造成的肋后能量低估问题, 对于优化临床治疗策略具有重要意义.During the treatment of subcostal lesions with high intensity focused ultrasound (HIFU), the obstruction by the ribs significantly affects the therapeutic effect, which can be assessed through numerical calculations. In existing studies, ribs are typically regarded as perfect acoustic absorbers, and even though this assumption could reveal the influence of the ribs on the acoustic field to some extent, it may still underestimate the energy behind the rib cage. In order to address the shortcomings of current work, an innovative numerical calculation method that avoids treating ribs as perfect sound absorbers is proposed in this work. Subsequently, experiments are conducted using ABS plastic rib cage mimic to compare the effectiveness between the two methods, demonstrating that the method proposed in this paper, which avoids the assumption of considering ribs as perfect acoustic absorbers, could better reveal the influence caused by ribs, and further studies are carried out on the influence of ribs in a multi-layered medium model. In response to the numerical oscillation issues encountered in existing work when dealing with media with high acoustic attenuation coefficients, the operator splitting method to enhance the stability of numerical calculations is adopted in this work. Furthermore, to tackle the challenges posed by asymmetric acoustic fields in numerical computations, in this paper matrix vectorization technique is introduced and stable solutions for the acoustic field under the backward implicit difference scheme are obtained. Additionally, when considering nonlinear effects, an asymptotic maximum number of harmonics is employed to reduce the computational load. These improvements in both the numerical calculation model and the corresponding algorithm not only enhance the precision of numerical computations, but also reveal the underestimation of energy behind the ribs due to the assumption of perfect acoustic absorbers, which is significant for optimizing HIFU treatment strategies.
-
Keywords:
- high intensity focused ultrasound /
- operator separation method /
- asymmetry /
- matrix vectorization
[1] Guang Z L P, Kristensen G, Røder A, Brasso K 2024 Clin. Genitourin. Cancer 22 102101
 Google Scholar
Google Scholar
[2] Schaudinn A, Michaelis J, Franz T, et al. 2021 Eur. J. Radiol. 144 109957
 Google Scholar
Google Scholar
[3] 蔡忠林, 刘强照, 王朝阳, 李慧, 周逢海 2017 现代肿瘤医学 25 2011
 Google Scholar
Google Scholar
Cai Z L, Liu Q Z, Wang C Y, Li H, Zhou F H 2017 Mod. Oncol. 25 2011
 Google Scholar
Google Scholar
[4] Zhang P, Xie L, Chen J, Zhan P, Xing H R, Yuan Y 2024 Ultrasound Med. Biol. 50 1381
 Google Scholar
Google Scholar
[5] Fan H J, Cun J P, Zhao W, Huang J Q, Yi G F, Yao R H, Gao B L, Li X H 2018 Int. J. Hyperthermia 35 534
 Google Scholar
Google Scholar
[6] 姚一静, 姜立新 2021 声学技术 40 376
 Google Scholar
Google Scholar
Yao Y J, Jiang L X 2021 Tech. Acoust. 40 376
 Google Scholar
Google Scholar
[7] Imankulov S B, Fedotovskikh G V, Shaimardanova G M, Yerlan M, Zhampeisov N K 2015 Ultrason. Sonochem. 27 712
 Google Scholar
Google Scholar
[8] Dupré A, Melodelima D, Cilleros C, De Crignis L, Peyrat P, Vincenot J, Rivoire M 2023 IRBM 44 100738
 Google Scholar
Google Scholar
[9] Li J L, Liu X Z, Zhang D, Gong X F 2007 Ultrasound Med. Biol. 33 1413
 Google Scholar
Google Scholar
[10] Yuldashev P V, Shmeleva S M, Ilyin S A, Sapozhnikov O A, Gavrilov L R, Khokhlova V A 2013 Phys. Med. Biol. 58 2537
 Google Scholar
Google Scholar
[11] Lin J X, Liu X Z, Gong X F, Ping Z H, Wu J R 2013 J. Acoust. Soc. Am. 134 1702
 Google Scholar
Google Scholar
[12] Kamakura T, Ishiwata T, Matsuda K 2000 J. Acoust. Soc. Am. 107 3035
 Google Scholar
Google Scholar
[13] Wang X, Lin J, Liu X J, Liu J Z, Gong X F 2016 Chin. Phys. B 25 044301
 Google Scholar
Google Scholar
[14] Zhao Y S, Gan Y, Long Y P, Sun F J, Fan X H 2024 Appl. Acoust. 216 109740
 Google Scholar
Google Scholar
[15] de Greef M, Schubert G, Wijlemans J W, Koskela J, Bartels L W, Moonen C T W, Ries M 2015 Med. Phys. 42 4685
 Google Scholar
Google Scholar
[16] Liu H L, Chang H, Chen W S, Shih T C, Hsiao J K, Lin W L 2007 Med. Phys. 34 3436
 Google Scholar
Google Scholar
[17] Liu H L, Hsu C L, Huang S M, Hsi Y W 2010 Med. Phys. 37 848
 Google Scholar
Google Scholar
[18] Sapareto S A, Dewey W C 1984 Int. J. Radiat. Oncol. Biol. Phys. 10 787
 Google Scholar
Google Scholar
[19] Cao R, Huang Z, Nabi G, Melzer A 2020 J. Ultrasound Med. 39 883
 Google Scholar
Google Scholar
[20] Khokhlova V A, Souchon R, Tavakkoli J, Sapozhnikov O A, Cathignol D 2001 J. Acoust. Soc. Am. 110 95
 Google Scholar
Google Scholar
[21] Fan T B, Liu Z B, Zhang Z, Zhang D, Gong X F 2009 Chin. Phys. Lett. 26 084302
 Google Scholar
Google Scholar
[22] Wear K A 2020 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 67 454
 Google Scholar
Google Scholar
[23] 钱盛友, 王鸿樟 2001 50 501
 Google Scholar
Google Scholar
Qian S Y, Wang H Z 2001 Acta Phys. Sin. 50 501
 Google Scholar
Google Scholar
[24] Khokhlova V, Shmeleva S, Gavrilov L 2010 Acoust. Phys. 56 665
 Google Scholar
Google Scholar
-
图 5 焦平面内声压峰峰值分布图 (a) $H\mathrm{_{FS}}= 64\; {\mathrm{mm}} $; (b) $H\mathrm{_{FS}}= 74\; {\mathrm{mm}} $; (c) $H\mathrm{_{FS}}= 84\; {\mathrm{mm}} $; (d) $H\mathrm{_{FS}}= 94\; {\mathrm{mm}} $
Fig. 5. Distribution of peak-to-peak pressure in the focal plane: (a) $H\mathrm{_{FS}}= 64\; {\mathrm{mm}} $; (b) $H\mathrm{_{FS}}= 74\; {\mathrm{mm}} $; (c) $H\mathrm{_{FS}}= 84\; {\mathrm{mm}} $; (d) $H\mathrm{_{FS}}= 94\; {\mathrm{mm}} $
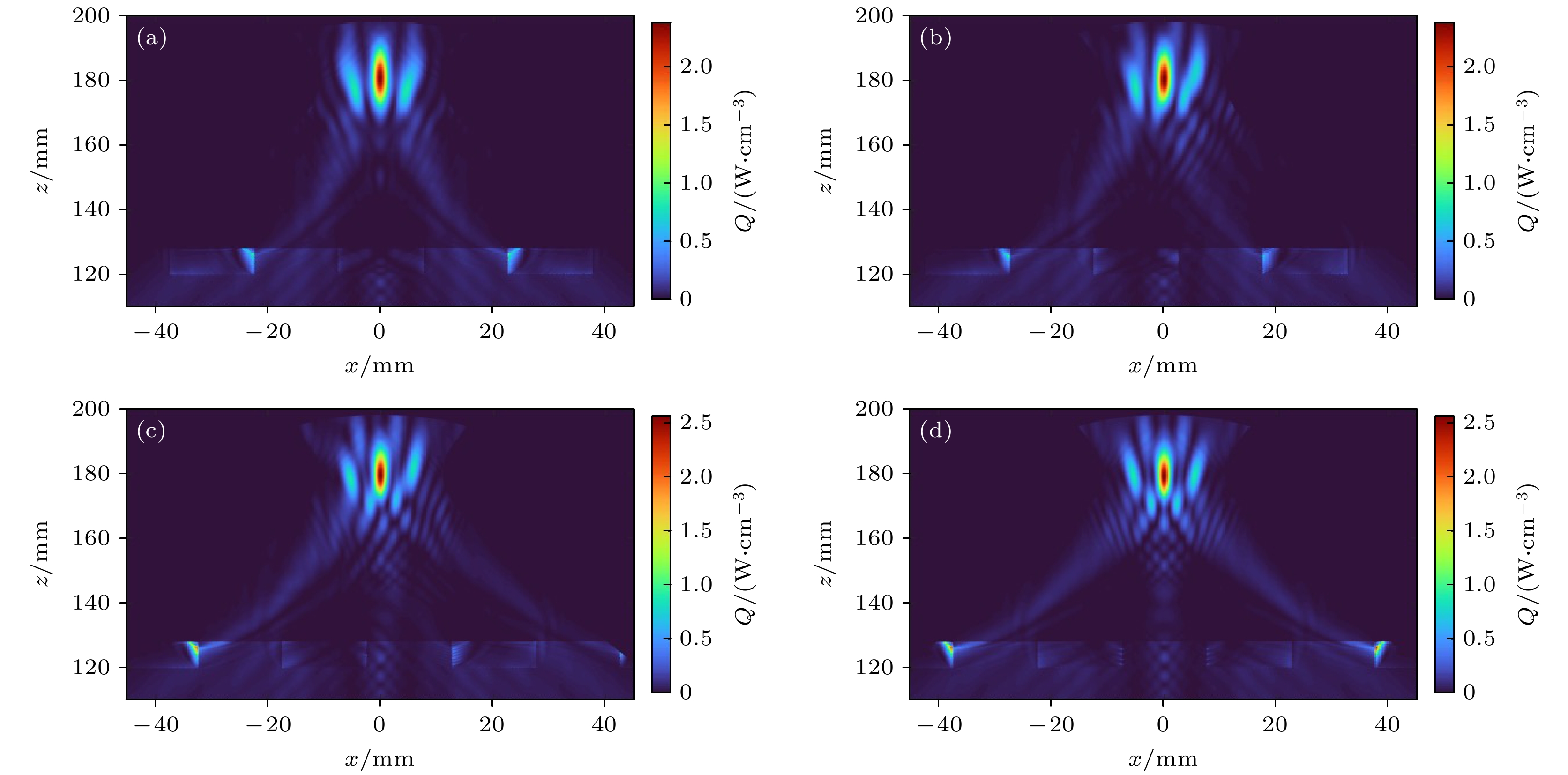
图 7 $ H\mathrm{_{FS} = 70 \;mm} $时热沉积速率在截面$ \varphi = 0 $内的分布 (a) $ x\mathrm{_c = 0\; mm} $; (b) $ x\mathrm{_c = 5 \;mm} $; (c) $ x\mathrm{_c = 10\; mm} $; (d) $ x\mathrm{_c = 15 \;mm} $
Fig. 7. Distribution of heat deposition rate in the $ \varphi = 0 $ plane with $ H\mathrm{_{FS} = 70 \;mm} $: (a) $ x\mathrm{_c = 0 \;mm} $; (b) $ x\mathrm{_c = 5 \;mm} $; (c) $ x\mathrm{_c = 10\; mm} $; (d) $ x\mathrm{_c = 15\; mm} $.
表 1 数值计算中使用的介质声参数
Table 1. Acoustic parameters of the medium used in numerical computation.
$ \rho/\left(\mathrm{kg \cdot m^{-3}} \right) $ $ c/\left(\mathrm{m\cdot s^{-1}} \right) $ $ \alpha/\left(\mathrm{Np\cdot {MHz}^{-\mu} \cdot m^{-1}} \right) $ μ β 水 1000 1500 0.025 2 3.5 脂肪 910 1430 9 1.15 10.5 肋骨 1450 2350 90 1 0 肝脏 1050 1596 4.5 1.13 6 表 2 $ H \mathrm{_{FS} = 70 \;mm} $时z轴上的声场参数
Table 2. Acoustic field’s parameters along the z-axis with $ H\mathrm{_{FS} = 70 \;mm} $.
$ x\mathrm{_c/mm} $ Field Ref 0 5 10 15 $ A\mathrm{_1}/p_0 $ 49.09 27.43 27.75 29.07 29.73 $ A\mathrm{_2}/p_0 $ 26.02 10.21 10.13 10.22 10.26 $ A\mathrm{_3}/p_0 $ 14.96 3.82 3.71 3.59 3.53 $ z\mathrm{_1/mm} $ 179.60 180.99 180.90 179.42 179.37 $ z\mathrm{_2/mm} $ 180.09 180.54 180.36 179.78 179.46 $ z\mathrm{_3/mm} $ 180.32 180.90 180.68 179.96 179.60 表 3 $ H \mathrm{_{FS} = 70 \;mm} $时平面$ \sigma = 0 $内的声场参数
Table 3. Acoustic field’s parameters in the $ \sigma = 0 $ plane with $ H \mathrm{_{FS} = 70 \;mm} $.
$ x\mathrm{_c/mm} $ Field Ref 0 5 10 15 $ \mathrm{WX_{1, -6\;dB}/mm} $ 3.22 3.39 3.21 2.86 2.71 $ \mathrm{WX_{2, -6\;dB}/mm} $ 1.90 1.91 1.83 1.62 1.53 $ \mathrm{WX_{3, -6\; dB}/mm} $ 1.46 1.40 1.36 1.23 1.18 $ \mathrm{WY_{1, -6\; dB}/mm} $ 3.22 3.12 3.13 3.23 3.27 $ \mathrm{WY_{2, -6\; dB}/mm} $ 1.90 1.80 1.80 1.84 1.86 $ \mathrm{WY_{3, -6\; dB}/mm} $ 1.46 1.39 1.39 1.39 1.39 -
[1] Guang Z L P, Kristensen G, Røder A, Brasso K 2024 Clin. Genitourin. Cancer 22 102101
 Google Scholar
Google Scholar
[2] Schaudinn A, Michaelis J, Franz T, et al. 2021 Eur. J. Radiol. 144 109957
 Google Scholar
Google Scholar
[3] 蔡忠林, 刘强照, 王朝阳, 李慧, 周逢海 2017 现代肿瘤医学 25 2011
 Google Scholar
Google Scholar
Cai Z L, Liu Q Z, Wang C Y, Li H, Zhou F H 2017 Mod. Oncol. 25 2011
 Google Scholar
Google Scholar
[4] Zhang P, Xie L, Chen J, Zhan P, Xing H R, Yuan Y 2024 Ultrasound Med. Biol. 50 1381
 Google Scholar
Google Scholar
[5] Fan H J, Cun J P, Zhao W, Huang J Q, Yi G F, Yao R H, Gao B L, Li X H 2018 Int. J. Hyperthermia 35 534
 Google Scholar
Google Scholar
[6] 姚一静, 姜立新 2021 声学技术 40 376
 Google Scholar
Google Scholar
Yao Y J, Jiang L X 2021 Tech. Acoust. 40 376
 Google Scholar
Google Scholar
[7] Imankulov S B, Fedotovskikh G V, Shaimardanova G M, Yerlan M, Zhampeisov N K 2015 Ultrason. Sonochem. 27 712
 Google Scholar
Google Scholar
[8] Dupré A, Melodelima D, Cilleros C, De Crignis L, Peyrat P, Vincenot J, Rivoire M 2023 IRBM 44 100738
 Google Scholar
Google Scholar
[9] Li J L, Liu X Z, Zhang D, Gong X F 2007 Ultrasound Med. Biol. 33 1413
 Google Scholar
Google Scholar
[10] Yuldashev P V, Shmeleva S M, Ilyin S A, Sapozhnikov O A, Gavrilov L R, Khokhlova V A 2013 Phys. Med. Biol. 58 2537
 Google Scholar
Google Scholar
[11] Lin J X, Liu X Z, Gong X F, Ping Z H, Wu J R 2013 J. Acoust. Soc. Am. 134 1702
 Google Scholar
Google Scholar
[12] Kamakura T, Ishiwata T, Matsuda K 2000 J. Acoust. Soc. Am. 107 3035
 Google Scholar
Google Scholar
[13] Wang X, Lin J, Liu X J, Liu J Z, Gong X F 2016 Chin. Phys. B 25 044301
 Google Scholar
Google Scholar
[14] Zhao Y S, Gan Y, Long Y P, Sun F J, Fan X H 2024 Appl. Acoust. 216 109740
 Google Scholar
Google Scholar
[15] de Greef M, Schubert G, Wijlemans J W, Koskela J, Bartels L W, Moonen C T W, Ries M 2015 Med. Phys. 42 4685
 Google Scholar
Google Scholar
[16] Liu H L, Chang H, Chen W S, Shih T C, Hsiao J K, Lin W L 2007 Med. Phys. 34 3436
 Google Scholar
Google Scholar
[17] Liu H L, Hsu C L, Huang S M, Hsi Y W 2010 Med. Phys. 37 848
 Google Scholar
Google Scholar
[18] Sapareto S A, Dewey W C 1984 Int. J. Radiat. Oncol. Biol. Phys. 10 787
 Google Scholar
Google Scholar
[19] Cao R, Huang Z, Nabi G, Melzer A 2020 J. Ultrasound Med. 39 883
 Google Scholar
Google Scholar
[20] Khokhlova V A, Souchon R, Tavakkoli J, Sapozhnikov O A, Cathignol D 2001 J. Acoust. Soc. Am. 110 95
 Google Scholar
Google Scholar
[21] Fan T B, Liu Z B, Zhang Z, Zhang D, Gong X F 2009 Chin. Phys. Lett. 26 084302
 Google Scholar
Google Scholar
[22] Wear K A 2020 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 67 454
 Google Scholar
Google Scholar
[23] 钱盛友, 王鸿樟 2001 50 501
 Google Scholar
Google Scholar
Qian S Y, Wang H Z 2001 Acta Phys. Sin. 50 501
 Google Scholar
Google Scholar
[24] Khokhlova V, Shmeleva S, Gavrilov L 2010 Acoust. Phys. 56 665
 Google Scholar
Google Scholar
计量
- 文章访问数: 2924
- PDF下载量: 34
- 被引次数: 0













 下载:
下载: