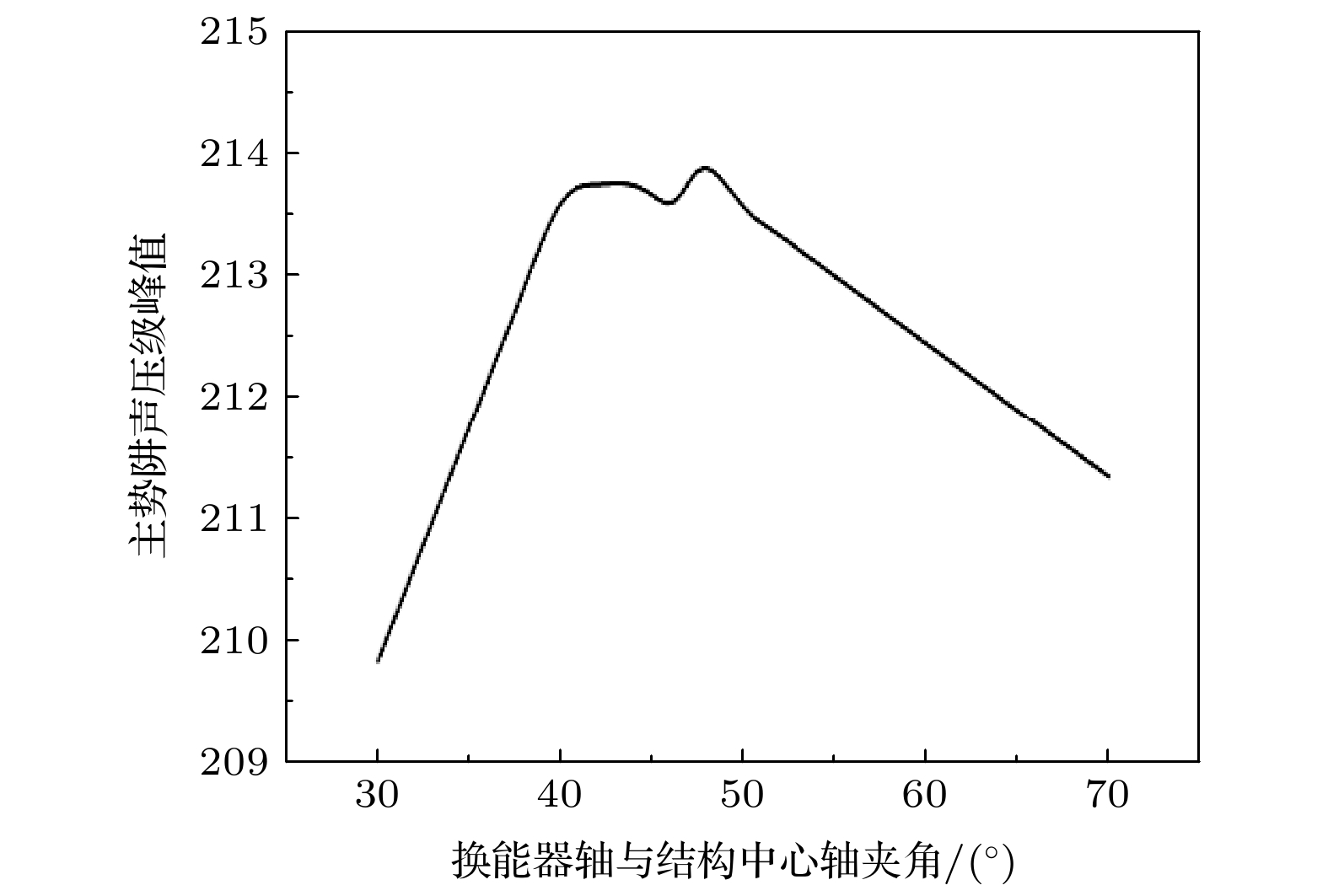
-
超声悬浮被广泛应用于多个领域, 目前主要有驻波式和相控阵式悬浮系统. 基于共焦点排列的聚焦换能器结构, 本研究提出了一种单边式超声悬浮系统. 其基本原理是利用反相激励成对聚焦换能器在空间构建具有势阱结构的特定声场, 实现微粒的捕获与悬浮. 针对4个共焦点排列的聚焦换能器, 基于有限元仿真研究了换能器轴夹角及激励相位模式对声场分布的影响; 利用实验演示了系统的粒子捕获效果, 验证了其势阱分布情况. 结果表明, 换能器轴线与结构中轴线夹角为45°时, 势阱强度最高; 换能器的激励相位分别为0, 0, π, π时, 声场中存在1处主势阱、2处次级势阱, 可以捕获3处粒子团; 换能器的激励相位分别为0, π/2, π, 3π/2时, 声场中仅存在1处势阱, 只可捕获1处粒子团. 该系统具有成本低、自由度高、稳定性强、操作便捷的优点, 且能够实现单个位置或多个位置粒子团的捕获与悬浮, 可以用于流体中高密度物体操控.The nonlinear effect of high-intensity sound waves produces the acoustic radiation force (ARF), which are used for acoustic levitation and manipulation practical. With no special requirement for the physical and chemical properties of the controlled objects, acoustic levitation owns a promising application prospect. The common levitation scheme includes the standing-wave system and phased-array levitation system. The standing-wave system has poor performance in the aspects of the degree of spatial freedom, the ARF along the non-axial direction, and the levitation stability. The phased-array system requires a complex control system and a high production cost. Here, we propose a single-side acoustic levitation system based on the paired confocal focused transducers. By driving the transducer pairs with reverse phase mode, two anti-phase focused spherical waves interfere with each other, resulting in constant sound pressure of 0 Pa at the focus. The resulting potential well can achieve stable particle capturing and levitating. First, we verifed the theoretical feasibility of the system according to Huygens' principle. Then, using the finite element method, we analyzed the influences of structural and driving parameters on the sound field distribution, such as the angle between the transducer axis and the central axis of the structure and the excitation phase modes. Finally, we demonstrated the particle trappings under two kinds of excitation phase modes of the levitation system experimentally. The results show that, 1) the intensity of the dominating potential well reaches a strongest value when the structural angle is 45°; 2) as the excitation phases are 0, 0, π, and π, the sound field owns three potential wells which can capture three clusters of quartz sands, the primary potential well is stronger than the secondary one; 3) as the excitation phases are 0, π/2, π, and 3π/2, the sound field owns one potential well and captures one cluster of quartz sands. The isosurface of wave intensity around the potential well is more comprehensive than in the previous phase mode. The four-phase excitation improves the levitation stability better. The proposed levitation scheme can realize stable single- or multi-position capture of high-density objects in the fluid. Moreover, it has the advantages of low cost and a high degree of freedom.
-
Keywords:
- acoustic levitation /
- acoustic potential well /
- focused transducer /
- particle capture
[1] Stindt A, Andrade M A B, Albrecht M, Adamowski J C, Panne U, Riedel J 2014 Rev. Sci. Instrum. 85 015
[2] Brandt E H 1989 Science 243 349
Google Scholar
[3] Li J, Jamieson W D, Dimitriou P, Xu W, Rohde P, Martinac B, Baker M, Drinkwater B W, Castell O K, Barrow D A 2022 Nat. Commun. 13 4125
Google Scholar
[4] Tait A, Glynne-Jones P, Hill A R, Smart D E, Blume C, Hammarstrom B, Fisher A L, Grossel M C, Swindle E J, Hill M, Davies D E 2019 Sci. Rep. 9 9789
Google Scholar
[5] Polychronopoulos S, Memoli G 2020 Sci. Rep. 10 4254
Google Scholar
[6] Morris R H, Dye E R, Axford D, Newton M I, Beale J H, Docker P T 2019 Sci. Rep. 9 12431
Google Scholar
[7] 冯乙婷, 姬晓亮, 张永建, Muhammad M M, 臧渡洋 2021 中国科学: 物理学 力学 天文学 5 147
Google Scholar
Feng Y T, Ji X L, Zhang Y J, Muhammad M M, Zang D Y 2021 Sci. Sin-Phys. Mech. Astron. 5 147
Google Scholar
[8] 张泽辉, 刘康祺, 邸文丽, 陈阵, 臧渡洋 2020 中国科学: 物理学 力学 天文学 50 113
Google Scholar
Zhang Z H, Liu K Q, Di W L, Chen Z, Zang D Y 2020 Sci. Sin-Phys. Mech. Astron. 50 113
Google Scholar
[9] Kepa M W, Tomizaki T, Sato Y, Ozerov D, Sekiguchi H, Yasuda N, Aoyama K, Skopintsev P, Standfuss J, Cheng R, Hennig M, Tsujino S 2022 Sci. Rep. 12 5349
Google Scholar
[10] Watanabe A, Hasegawa K, Abe Y 2018 Sci. Rep. 8 1
[11] 魏衍举, 张洁, 邓胜才, 张亚杰, 杨亚晶, 刘圣华, 陈昊 2020 69 184702
Google Scholar
Wei Y J, Zhang J, Deng S C, Zhang Y J, Yang Y J, Liu S H, Chen H 2020 Acta Phys. Sin. 69 184702
Google Scholar
[12] Foresti D, Nabavi M, Klingauf M, Ferrari A, Poulikakos D 2013 PNAS 110 12549
Google Scholar
[13] 秦修培, 耿德路, 洪振宇, 魏炳波 2017 66 124301
Google Scholar
Qin X P, Geng D L, Hong Z Y, Wei B B 2017 Acta Phys. Sin. 66 124301
Google Scholar
[14] 洪振宇, 吕勇军, 解文军, 魏炳波 2006 科学通报 1 2714
Google Scholar
Hong Z Y, Lyu Y J, Xie W J and Wei B B 2006 Chin. Sci. Bull. 1 2714
Google Scholar
[15] 阮永都, 梁旭 2020 中国科学: 技术科学 50 1226
Google Scholar
Ruan Y D, Liang X 2020 Sci. Sinica Tec. ) 50 1226
Google Scholar
[16] Marzo Pérez A, Seah S A, Drinkwater B W, Sahoo D R, Long B, Subramanian S 2015 Nat. Commun. 6 8661
Google Scholar
[17] Fushimi T, Yamamoto K, Ochiai Y 2021 Sci. Rep. 11 12678
Google Scholar
[18] 范皓然, 尹冠军, 李盼, 郭建中 2018 声学学报 43 364
Fan H R,Yin G J, Li P, Guo J Z 2018 Acta Acust. 43 364
[19] Roslyakov S, Emelyanov F, Erzakova N, Sivkov E 2019 IOP Conference 516 012033
Google Scholar
[20] Wei L L, Yin G J, Han H, Guo J Z 2021 International Ultrasonics Symposium (IUS) Xi'an, China, November 16, 2021 pp1–4
[21] 朱哲民, 龚秀芬, 杜功焕 2012 声学基础(第三版) (南京: 南京大学出版社) 第211—220页
Zhu Z M, Gong X F, Du G H 2012 Fundamentals of Acoustics (Vol. 3) (Nanjing: Nanjing University Press) pp211–220 (in Chinese)
-
图 2 数值仿真的结构模型和相位模式 (a) 结构模型图; (b) 两相位激励模式; (c) 四相位激励模式
Fig. 2. Structure model and phase mode in the numerical simulations: (a) Structure model; (b) two-phase excitation model; (c) four-phase excitation model.
图 3 主势阱声压级峰值随换能器夹角变化图
Fig. 3. The relationship between the peak value of sound pressure level in the primary potential well and the angle of the transducer.
图 4 两相位模式的声强切面图 (白色实线圈为主势阱位置, 白色虚线圈为次级势阱位置) (a) x-y截面 (z = 0 mm); (b) y-z截面 (主势阱) (x = 0 mm); (c) y-z截面 (次级势阱) (x = 0.2 mm)
Fig. 4. Sound intensity of the two-phase model (The white solid coil is the main potential well position, and the white dashed coil is the secondary potential well position): (a) x-y section (z = 0 mm); (b) y-z section (the primary potential well) (x = 0 mm); (c) y-z section (the secondary potential well) (x = 0.2 mm).
图 5 两相位模式的声强等值面 (白色实线圈为主势阱位置, 白色虚线圈为次级势阱位置) (a) Is = 1.31 kW/m2; (b) Is = 0.53 kW/m2; (c) Is = 0.53 kW/m2
Fig. 5. Equipotential surface of sound intensity of the two-phase model (The white solid coil is the main potential well, and the white dashed coil is the secondary potential well.): (a) Is = 1.31 kW/m2; (b) Is = 0.53 kW/m2; (c) Is = 0.53 kW/m2.
图 6 四相位模式的声强切面图(白色实线圈为主势阱位置) (a)x-y截面 (z = 0 mm); (b)y-z截面 (x = 0 mm); (c)x-z截面 (y = 0 mm)
Fig. 6. Sound intensity of the four-phase model (The white solid coil is the main potential well): (a) x-y section (z = 0 mm); (b) y-z section (x = 0 mm); (c) x-z section (y = 0 mm).
图 7 四相位模式的声强等值面图 (a) Is = 3.0 kW/m2; (b) Is = 1.2 kW/m2; (c) Is = 1.2 kW/m2
Fig. 7. Equipotential surface of sound intensity of the four-phase model: (a) Is = 3.0 kW/m2; (b) Is = 1.2 kW/m2; (c) Is = 1.2 kW/m2
图 9 实验结果图 (a)两相位模式结果; (b)四相位模式结果
Fig. 9. Picture of experimental results: (a) Result of two-phase model; (b) result of four-phase model.
-
[1] Stindt A, Andrade M A B, Albrecht M, Adamowski J C, Panne U, Riedel J 2014 Rev. Sci. Instrum. 85 015
[2] Brandt E H 1989 Science 243 349
Google Scholar
[3] Li J, Jamieson W D, Dimitriou P, Xu W, Rohde P, Martinac B, Baker M, Drinkwater B W, Castell O K, Barrow D A 2022 Nat. Commun. 13 4125
Google Scholar
[4] Tait A, Glynne-Jones P, Hill A R, Smart D E, Blume C, Hammarstrom B, Fisher A L, Grossel M C, Swindle E J, Hill M, Davies D E 2019 Sci. Rep. 9 9789
Google Scholar
[5] Polychronopoulos S, Memoli G 2020 Sci. Rep. 10 4254
Google Scholar
[6] Morris R H, Dye E R, Axford D, Newton M I, Beale J H, Docker P T 2019 Sci. Rep. 9 12431
Google Scholar
[7] 冯乙婷, 姬晓亮, 张永建, Muhammad M M, 臧渡洋 2021 中国科学: 物理学 力学 天文学 5 147
Google Scholar
Feng Y T, Ji X L, Zhang Y J, Muhammad M M, Zang D Y 2021 Sci. Sin-Phys. Mech. Astron. 5 147
Google Scholar
[8] 张泽辉, 刘康祺, 邸文丽, 陈阵, 臧渡洋 2020 中国科学: 物理学 力学 天文学 50 113
Google Scholar
Zhang Z H, Liu K Q, Di W L, Chen Z, Zang D Y 2020 Sci. Sin-Phys. Mech. Astron. 50 113
Google Scholar
[9] Kepa M W, Tomizaki T, Sato Y, Ozerov D, Sekiguchi H, Yasuda N, Aoyama K, Skopintsev P, Standfuss J, Cheng R, Hennig M, Tsujino S 2022 Sci. Rep. 12 5349
Google Scholar
[10] Watanabe A, Hasegawa K, Abe Y 2018 Sci. Rep. 8 1
[11] 魏衍举, 张洁, 邓胜才, 张亚杰, 杨亚晶, 刘圣华, 陈昊 2020 69 184702
Google Scholar
Wei Y J, Zhang J, Deng S C, Zhang Y J, Yang Y J, Liu S H, Chen H 2020 Acta Phys. Sin. 69 184702
Google Scholar
[12] Foresti D, Nabavi M, Klingauf M, Ferrari A, Poulikakos D 2013 PNAS 110 12549
Google Scholar
[13] 秦修培, 耿德路, 洪振宇, 魏炳波 2017 66 124301
Google Scholar
Qin X P, Geng D L, Hong Z Y, Wei B B 2017 Acta Phys. Sin. 66 124301
Google Scholar
[14] 洪振宇, 吕勇军, 解文军, 魏炳波 2006 科学通报 1 2714
Google Scholar
Hong Z Y, Lyu Y J, Xie W J and Wei B B 2006 Chin. Sci. Bull. 1 2714
Google Scholar
[15] 阮永都, 梁旭 2020 中国科学: 技术科学 50 1226
Google Scholar
Ruan Y D, Liang X 2020 Sci. Sinica Tec. ) 50 1226
Google Scholar
[16] Marzo Pérez A, Seah S A, Drinkwater B W, Sahoo D R, Long B, Subramanian S 2015 Nat. Commun. 6 8661
Google Scholar
[17] Fushimi T, Yamamoto K, Ochiai Y 2021 Sci. Rep. 11 12678
Google Scholar
[18] 范皓然, 尹冠军, 李盼, 郭建中 2018 声学学报 43 364
Fan H R,Yin G J, Li P, Guo J Z 2018 Acta Acust. 43 364
[19] Roslyakov S, Emelyanov F, Erzakova N, Sivkov E 2019 IOP Conference 516 012033
Google Scholar
[20] Wei L L, Yin G J, Han H, Guo J Z 2021 International Ultrasonics Symposium (IUS) Xi'an, China, November 16, 2021 pp1–4
[21] 朱哲民, 龚秀芬, 杜功焕 2012 声学基础(第三版) (南京: 南京大学出版社) 第211—220页
Zhu Z M, Gong X F, Du G H 2012 Fundamentals of Acoustics (Vol. 3) (Nanjing: Nanjing University Press) pp211–220 (in Chinese)
下载:
计量
- 文章访问数: 4419
- PDF下载量: 85
- 被引次数: 0
