-
从声散射基本理论出发, 考虑弹性粒子与空化泡之间耦合作用, 结合边界条件, 推导了弹性粒子外部声流分布, 得到了声微流的n = 0和n = 1模式近似表达式和粒子表面应力分布函数. 数值分析结果表明: 气泡和弹性粒子之间的耦合作用增加了粒子周围的微流分布与剪应力场分布, 特别是微流速度的切向分量. 随着两者间距与相对位置的距离增大, 粒子与气泡之间相互作用减弱, 粒子周围微流幅值减小; 当气泡处于共振状态时, 粒子周围的微流分布显著增强. 粒子表面剪应力场受粒子半径与声场频率影响, 当粒子半径与声场频率越大, 外部散射声强越强, 粒子表面剪应力幅值越大.In this paper, the interaction between elastic particle and cavitation bubble is considered, the expression of microstreaming velocity and shear stress around the elastic particle are derived by using the theory of acoustic scattering. Taking into account the two predominant modes of elastic particle: n = 0 mode and n = 1 mode, the effects of the distance and the ratio of the radius and the relative position on microstreaming distribution, and the effects of the particle radius and the driving frequency on shear stress distribution are investigated. It is demonstrated that the interaction can increase the amplitude of microstreaming velocity, especially the tangential component of microstreaming velocity, and the shear stress. As the distance between elastic particle and cavitation bubble increases, the interaction weakens and the amplitude of the microstreaming velocity around the elastic particle decreases. When the bubble is in resonance, the microstreaming velocity around the elastic particle is significantly enhanced. The shear stress of the particle is affected by the particle radius and the frequency of sound field. As the particle radius and the frequency of sound field are larger, the external scattering sound becomes stronger and the amplitude of shear stress on the surface of particles turns larger.
-
Keywords:
- elastic particle /
- cavitation bubble /
- microstreaming /
- acoustic scattering
[1] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[2] Marberger M, Stackl W, Hruby W, Wurster H, Schnedl W 1985 World J. Urol. 3 27
Google Scholar
[3] 梁金福, 陈伟中, 邵纬航, 周超, 杜联芳, 金利芳 2013 62 084708
Google Scholar
Liang J F, Chen W Z, Shao W H, Zhou C, Du L F, Jin L F 2013 Acta Phys. Sin. 62 084708
Google Scholar
[4] 于洁, 郭霞生, 屠娟, 章东 2015 64 094306
Google Scholar
Yu J, Guo X S, Tu J, Zhang D 2015 Acta Phys. Sin. 64 094306
Google Scholar
[5] Kolb J, Nyborg W L 1956 J. Acoust. Soc. Am. 28 1237
Google Scholar
[6] 吴文华, 翟薇, 胡海豹, 魏炳波 2017 66 194303
Google Scholar
Wu W H, Zhai W, Hu H B, Wei B B 2017 Acta Phys. Sin. 66 194303
Google Scholar
[7] Elder, Samuel A 1959 J. Acoust. Soc. Am. 31 54
Google Scholar
[8] Wu J R, Du G H 1997 J. Acoust. Soc. Am. 101 1899
Google Scholar
[9] Liu X Z, Wu J R 2009 J. Acoust. Soc. Am. 125 1319
Google Scholar
[10] Doinikov A A, Bouakaz A 2010 J. Acoust. Soc. Am. 127 1218
Google Scholar
[11] Doinikov A A, Bouakaz A 2010 J. Acoust. Soc. Am. 127 703
Google Scholar
[12] Manasseh R, Tho P, Ooi A, Petkovic-Duran K, Zhu Y 2010 Phys. Procedia 3 427
Google Scholar
[13] Collis J, Manasseh R, Liovic P, Tho P, Ooi A, Petkovic-Duran K, Zhu Y 2010 Ultrasonics 50 273
Google Scholar
[14] Doinikov A A, Bouakaz A 2016 J. Fluid Mech. 796 318
Google Scholar
[15] Doinikov A A, Ayache B 2014 J. Fluid Mech. 742 425
Google Scholar
[16] Tho P, Manasseh R, Ooi A 2007 J. Fluid Mech. 122 191
Google Scholar
[17] Wang L, Tu J, Guo X S, Xu D, Zhang D 2014 Chin. Phys. B 23 124302
Google Scholar
[18] Wang C, Cheng J 2013 J. Acoust. Soc. Am. 134 1675
Google Scholar
[19] 武耀蓉, 王成会, 莫润阳, 陈时 2017 陕西师范大学学报(自然科学版) 45 50
Wu Y R, Wang C H, Mo R Y, Chen S 2017 J. Shaanxi Normal Univ. (Nat. Sci. Ed.) 45 50
[20] 武耀蓉, 王成会, 陈时 2017 南京大学学报 (自然科学版) 53 1
Wu Y R, Wang C H, Chen S 2017 J. Nanjing Univ. (Nat. Sci. Ed.) 53 1
[21] Hasegawa T, Ochi M, Matsuzawa K 1969 J. Acoust. Soc. Am. 46 1139
Google Scholar
[22] L in, Wen H 1983 J. Acoust. Soc. Am. 73 736
Google Scholar
[23] Li S, Han R, Zhang A M 2016 J. Fluid. Struct. 65 333
Google Scholar
[24] Shi J, Yang D S, Zhang H Y, Shi S G, Li S, Hu B 2017 Chin. Phys. B 26 074301
Google Scholar
-
图 2
${\theta _1}$ 对弹性粒子壁面流速场分布影响 (a)$n = 0$ 模式; (b)$n = 1$ 模式Fig. 2. Streaming as a function of
${\theta _1}$ : (a)$n = 0$ mode; (b)$n = 1$ mode.
图 5 弹性粒子壁面的剪应力分布 (a)与(b)初始半径分别为7.5, 15, 30 μm; (c)与(d)驱动频率分别为80, 100, 120 kHz
Fig. 5. Shear stresses versus
${\theta _1}$ : (a) and (b) The radius is equal to 7.5, 15, 30 μm; (c) and (d) the driving frequency is equal to 80, 100, 120 kHz.
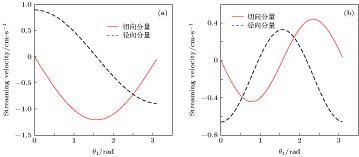
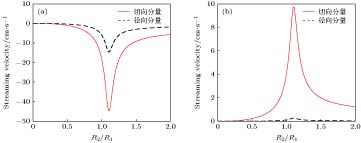
图 3
${{{r_1}} / {{R_1}}}\;\left( {\theta = {{\text{π}} / 4}} \right)$ 和${{D'} / {{R_1}}}\;(D' = D - {R_1} - {R_2}, {\theta _1} = {{\text{π}} / 4})$ 对弹性粒子壁面微流分布影响 (a)与(c)$n = 0$ 模式; (b)与(d)$n = 1$ 模式Fig. 3. Streaming as a function of
${{{r_1}} / {{R_1}}}$ $\left( {\theta = {{\text{π}} / 4}} \right)$ and${{D'} / {{R_1}}}\;(D' = D - {R_1} - {R_2}, {\theta _1} = {{\text{π}} / 4})$ : (a) and (c)$n = 0$ mode; (b) and (d)$n = 1$ mode.
图 4
${{{R_2}} / {{R_1}}}\;({\theta _1} = {{\text{π}} / 4})$ 对弹性粒子壁面微流分布影响 (a)$n = 0$ 模式; (b)$n = 1$ 模式Fig. 4. Streaming as a function of
${{{R_2}} / {{R_1}}}\;({\theta _1} = {{\text{π}} / 4}):$ (a)$n = 0$ mode; (b)$n = 1$ mode. -
[1] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[2] Marberger M, Stackl W, Hruby W, Wurster H, Schnedl W 1985 World J. Urol. 3 27
Google Scholar
[3] 梁金福, 陈伟中, 邵纬航, 周超, 杜联芳, 金利芳 2013 62 084708
Google Scholar
Liang J F, Chen W Z, Shao W H, Zhou C, Du L F, Jin L F 2013 Acta Phys. Sin. 62 084708
Google Scholar
[4] 于洁, 郭霞生, 屠娟, 章东 2015 64 094306
Google Scholar
Yu J, Guo X S, Tu J, Zhang D 2015 Acta Phys. Sin. 64 094306
Google Scholar
[5] Kolb J, Nyborg W L 1956 J. Acoust. Soc. Am. 28 1237
Google Scholar
[6] 吴文华, 翟薇, 胡海豹, 魏炳波 2017 66 194303
Google Scholar
Wu W H, Zhai W, Hu H B, Wei B B 2017 Acta Phys. Sin. 66 194303
Google Scholar
[7] Elder, Samuel A 1959 J. Acoust. Soc. Am. 31 54
Google Scholar
[8] Wu J R, Du G H 1997 J. Acoust. Soc. Am. 101 1899
Google Scholar
[9] Liu X Z, Wu J R 2009 J. Acoust. Soc. Am. 125 1319
Google Scholar
[10] Doinikov A A, Bouakaz A 2010 J. Acoust. Soc. Am. 127 1218
Google Scholar
[11] Doinikov A A, Bouakaz A 2010 J. Acoust. Soc. Am. 127 703
Google Scholar
[12] Manasseh R, Tho P, Ooi A, Petkovic-Duran K, Zhu Y 2010 Phys. Procedia 3 427
Google Scholar
[13] Collis J, Manasseh R, Liovic P, Tho P, Ooi A, Petkovic-Duran K, Zhu Y 2010 Ultrasonics 50 273
Google Scholar
[14] Doinikov A A, Bouakaz A 2016 J. Fluid Mech. 796 318
Google Scholar
[15] Doinikov A A, Ayache B 2014 J. Fluid Mech. 742 425
Google Scholar
[16] Tho P, Manasseh R, Ooi A 2007 J. Fluid Mech. 122 191
Google Scholar
[17] Wang L, Tu J, Guo X S, Xu D, Zhang D 2014 Chin. Phys. B 23 124302
Google Scholar
[18] Wang C, Cheng J 2013 J. Acoust. Soc. Am. 134 1675
Google Scholar
[19] 武耀蓉, 王成会, 莫润阳, 陈时 2017 陕西师范大学学报(自然科学版) 45 50
Wu Y R, Wang C H, Mo R Y, Chen S 2017 J. Shaanxi Normal Univ. (Nat. Sci. Ed.) 45 50
[20] 武耀蓉, 王成会, 陈时 2017 南京大学学报 (自然科学版) 53 1
Wu Y R, Wang C H, Chen S 2017 J. Nanjing Univ. (Nat. Sci. Ed.) 53 1
[21] Hasegawa T, Ochi M, Matsuzawa K 1969 J. Acoust. Soc. Am. 46 1139
Google Scholar
[22] L in, Wen H 1983 J. Acoust. Soc. Am. 73 736
Google Scholar
[23] Li S, Han R, Zhang A M 2016 J. Fluid. Struct. 65 333
Google Scholar
[24] Shi J, Yang D S, Zhang H Y, Shi S G, Li S, Hu B 2017 Chin. Phys. B 26 074301
Google Scholar
下载:
计量
- 文章访问数: 6863
- PDF下载量: 80
- 被引次数: 0
