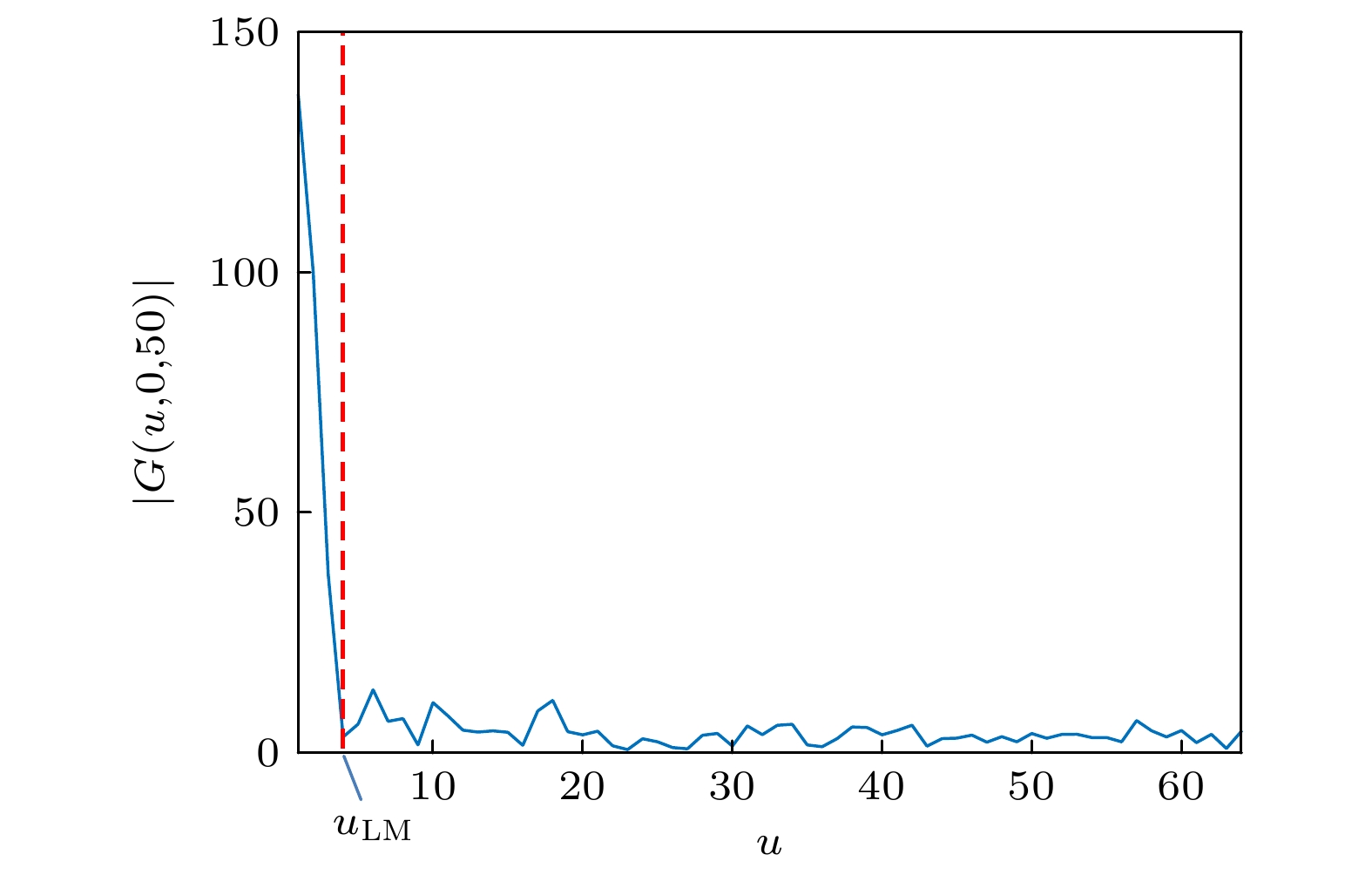
-
非视域成像是对探测器视线外被遮挡的物体进行光学成像的新兴技术, 基于光锥变换反演法的非视域成像可以看作是一个反卷积的过程, 传统维纳滤波反卷积方法是使用经验值或者反复尝试得到瞬态图像的功率谱密度噪信比(power spectral density noise-to-signal ratio, PSDNSR)进行维纳滤波反卷积, 但非视域成像每个隐藏场景的PSDNSR都不同, 先验估计难以适用. 因此本文提出使用捕获瞬态图像的中频域信息来估计PSDNSR进行维纳滤波从而实现非视域成像. 实验表明, 基于中频域维纳滤波的非视域成像算法估计的PSDNSR能够落在一个重建效果较好的量级上. 相比其他方法, 本文算法能一步直接估计出PSDNSR, 没有迭代运算, 计算复杂度低, 能够在保证重建效果的前提下提升重建效率.Non-line-of-sight (NLOS) imaging is an emerging technology for optically imaging the objects blocked beyond the detector's line of sight. The NLOS imaging based on light-cone transform and inverted method can be regarded as a deconvolution process. The traditional Wiener filtering deconvolution method uses the empirical values or the repeated attempts to obtain the power spectral density noise-to-signal ratio (PSDNSR) of the transient image: each hidden scene has a different PSDNSR for NLOS imaging, so the prior estimation is not appropriate and repeated attempts make it difficult to quickly find the optimal value. Therefore, in this work proposed is a method of estimating the PSDNSR by using the mid-frequency information of captured transient images for Wiener filtering to achieve NLOS imaging. In this method, the turning points between the mid-frequency domain and the high-frequency domain of the transient image amplitude spectrum are determined, and then the PSDNSR value is solved by analyzing the characteristics and relationship among the noise power spectra at the low, middle and high frequency. Experiments show that the PSDNSR estimated by NLOS imaging algorithm based on Wiener filtering of mid-frequency domain has a better reconstruction effect. Compared with other methods, the algorithm in this work can directly estimate PSDNSR in one step, without iterative operations, and the computational complexity is low, therebysimplifying the parameter adjustment steps of the Wiener filtering deconvolution NLOS imaging algorithm based on light-cone transform. Therefore the reconstruction efficiency can be improved on the premise of ensuring the reconstruction effect.
-
Keywords:
- non-line-of-sight imaging /
- light-cone transform /
- deconvolution /
- mid-frequency
[1] Laurenzis M, Velten A 2014 J. Electron. Imaging 23 063003
Google Scholar
[2] Chan S, Warburton R E, Gariepy G, Leach J, Faccio D 2017 Opt. Express 25 10109
Google Scholar
[3] Bouman K L, Ye V, Yedidia A B, Durand F, Wornell G W, Torralba A, Freeman W T 2017 Proceedings of the IEEE International Conference on Computer Vision Venice, Italy, October 22–29, 2017 pp2270–2278
[4] Musarra G, Lyons A, Conca E, Altmann Y, Villa F, Zappa F, Padgett M J, Faccio D 2019 Phys. Rev. Appl. 12 011002
Google Scholar
[5] Liu X C, Guillén I, La Manna M, Nam J H, Reza S A, Huu Le T, Jarabo A, Gutierrez D, Velten A 2019 Nature 572 620
Google Scholar
[6] Xin S, Nousias S, Kutulakos K N, et al. 2019 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Long Beach, CA, USA, June 15–20, 2019 pp6800–6809
[7] Wang B, Zheng M Y, Han J J, Huang X, Xie X P, Xu F H, Zhang Q, Pan J W 2021 Phys. Rev. Lett. 127 053602
Google Scholar
[8] Kirmani A, Hutchison T, Davis J, Raskar R 2009 2009 IEEE 12 th International Conference on Computer Vision Kyoto, Japan, September 29–Octorber 2, 2009 pp159–166
[9] Velten A, Willwacher T, Gupta O, Veeraraghavan A, Bawendi M G, Raskar R 2012 Nat. Commun. 3 1
[10] Klein J, Laurenzis M, Hullin M 2016 Electro-Optical Remote Sensing X Edinburgh, UK, September 26–29, 2016 p998802
[11] O’Toole M, Lindell D B, Wetzstein G 2018 Nature 555 338
Google Scholar
[12] 任禹, 罗一涵, 徐少雄, 马浩统, 谭毅 2021 光电工程 48 200124
Ren Y, Luo Y H, Xu S X, Ma H T, Tan Y 2021 Opto-Electron. Eng. 48 200124 (in Chinese)
[13] Jin C F, Xie J H, Zhang S Q, Zhang Z, Zhao Y 2018 Opt. Express 26 20089
Google Scholar
[14] Arellano V, Gutierrez D, Jarabo A 2017 Opt. Express 25 11574
Google Scholar
[15] Wu C, Liu J J, Huang X, Li Z P, Yu C, Ye J T, Zhang J, Zhang Q, Dou X K, Goyal V K 2021 P. Natl. Acad. Sci. 118 e2024468118
Google Scholar
[16] Satat G, Tancik M, Gupta O, Heshmat B, Raskar R 2017 Opt. Express 25 17466
Google Scholar
[17] Caramazza P, Boccolini A, Buschek D, Hullin M, Higham C F, Henderson R, Murray-Smith R, Faccio D 2018 Sci. Rep-uk. 8 1
[18] Musarra G, Caramazza P, Turpin A, Lyons A, Higham C F, Murray-Smith R, Faccio D 2019 Advanced Photon Counting Techniques XIII Baltimore, Maryland, United States, May 13, 2019 p1097803
[19] Isogawa M, Yuan Y, O'Toole M, Kitani K M 2020 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Seattle, WA, USA, June 13–19, 2020 pp7013–7022
[20] Gariepy G, Tonolini F, Henderson R, Leach J, Faccio D 2016 Nat. Photonics 10 23
Google Scholar
[21] Hullin M B 2014 Optoelectronic Imaging and Multimedia Technology III Beijing, China, October 29, 2014 pp197–204
[22] Luo Y H, Fu C Y 2011 Opt Eng 50 047004
Google Scholar
[23] 许丽娜, 肖奇, 何鲁晓 2019 武汉大学学报(信息科学版) 44 546
Xu L N, Xiao Q, He L X 2019 Geomat. Inf. Sci. Wuhan Univ. 44 546
-
图 1 实验场景示意图, 激光通过振镜对中介面扫描, 探测器接收来自中介面反射的直接光和来自隐藏物体的间接光
Fig. 1. Experimental scene, the laser scans the intermediate surface through the galvanometer, and the detector receives direct light reflected from the intermediate surface and indirect light from a hidden object.
图 2
$ w = 50 $ 时瞬态图像的频谱图$ \left| {G(u, v, w)} \right| $ Fig. 2. Spectrum
$ \left| {G(u, v, w)} \right| $ of the transient image at$ w = 50 $ .
图 3 幅度
$ \left| {G(u, v, w)} \right| $ 中过原点的一条线$ \left| {G(u, 0, 50)} \right| $ Fig. 3. A line
$ \left| {G(u, 0, 50)} \right| $ through the origin in the spectral magnitude$ \left| {G(u, v, w)} \right| $ .
图 4 幅度
$ \ln \left| {G(u, 0, 50)} \right| $ 平滑之后的曲线$ {G_r}(u) $ Fig. 4. Curve
$ {G_r}(u) $ after amplitude$ \ln \left| {G(u, 0, 50)} \right| $ smoothing.
图 5
$ u = 0 $ 时瞬态图像的频谱图$ \left| {G(u, v, w)} \right| $ Fig. 5. Spectrum
$ \left| {G(u, v, w)} \right| $ of the transient image at$ u = 0 $ .
图 6 幅度
$ \left| {G(u, v, w)} \right| $ 中过原点的一条线$ \left| {G(0, 0, w)} \right| $ Fig. 6. A line
$ \left| {G(0, 0, w)} \right| $ through the origin in the spectral magnitude$ \left| {G(u, v, w)} \right| $ .
图 7 实验场景 (a)为在实验室搭建的共焦非视域成像场景; (b)为共焦非视域成像系统
Fig. 7. Experimental scene: (a) The confocal non-horizontal imaging scene built in the laboratory; (b) demonstrates the confocal non-horizontal imaging system.
图 8 隐藏场景 (a) T形纸板; (b)人偶模型手臂向下; (c)房屋形纸板; (d)C形纸板; (e)人偶模型手臂向上
Fig. 8. Hidden scene: (a) T-shaped cardboard; (b) puppet model with arms down; (c) house-shaped cardboard; (d) C- shaped cardboard; (e) puppet model with arms up.
图 9 隐藏物体T形纸板和基于中频域的维纳滤波的重建结果
Fig. 9. T-shaped cardboard and reconstruction results of NLOS imaging based on mid-frequency Wiener filtering.
图 10 传统维纳滤波的重建结果与基于中频域的维纳滤波的重建结果对比 (a)−(f) T形纸板的隐藏场景分别取K为0.01, 0.1, 1, 10, 100, 1000进行维纳滤波复原的结果; (h) T形纸板基于中频域的维纳滤波重建的结果, 估出K为2.8678
Fig. 10. Comparison between the reconstruction results of traditional Wiener filtering and the reconstruction results based on Wiener filtering in the mid-frequency domain: (a)−(f) The results of Wiener filtering reconstruction with K as 0.01, 0.1, 1, 10, 100, and 1000 for T-shaped cardboard respectively; (h) the reconstruction result of T-shaped cardboard using the NLOS imaging algorithm based on Wiener filtering of mid-frequency domain, and the estimated K is 2.8678.
图 11 隐藏场景人偶模型手臂向下和基于中频域的维纳滤波的重建结果
Fig. 11. Puppet model with arms down and reconstruction results of NLOS imaging based on mid-frequency Wiener filtering.
图 12 传统维纳滤波的重建结果与基于中频域的维纳滤波的重建结果对比 (a)−(f)人偶模型隐藏场景分别取K为0.01, 0.1, 1, 10, 100, 1000进行维纳滤波复原的结果; (h)人偶模型隐藏场景基于中频域的维纳滤波重建的结果, 估计出的K为1.2353
Fig. 12. Comparison between the reconstruction results of traditional Wiener filtering and the reconstruction results based on Wiener filtering in the mid-frequency domain: (a)−(f) The results of Wiener filtering reconstruction with K as 0.01, 0.1, 1, 10, 100, and 1000 for puppet model with arms down respectively; (h) the reconstruction result of puppet model with arms down using the NLOS imaging algorithm based on Wiener filtering of mid-frequency domain, and the estimated K is 1.2353.
图 13 隐藏场景房屋形纸板和基于中频域的维纳滤波的重建结果
Fig. 13. House-shaped cardboard and reconstruction results of NLOS imaging based on mid-frequency Wiener filtering.
图 14 传统维纳滤波的重建结果与基于中频域的维纳滤波的重建结果对比 (a)−(f)为房屋形纸板的隐藏场景分别取K为0.01, 0.1, 1, 10, 100, 1000进行维纳滤波复原的结果; (h)房屋形纸板隐藏场景基于中频域的维纳滤波重建的结果, 估计出的K为3.6711
Fig. 14. Comparison between the reconstruction results of traditional Wiener filtering and the reconstruction results based on Wiener filtering in the mid-frequency domain: (a)−(f) The results of Wiener filtering reconstruction with K as 0.01, 0.1, 1, 10, 100, and 1000 for House-shaped cardboard respectively; (h) the reconstruction result of house-shaped cardboard using the NLOS imaging algorithm based on Wiener filtering of mid-frequency domain, and the estimated K is 3.6711.
图 15 隐藏场景C形纸板和基于中频域的维纳滤波的重建结果
Fig. 15. C- shaped cardboard and reconstruction results of NLOS imaging based on mid-frequency Wiener filtering.
图 17 隐藏场景人偶模型手臂向上和基于中频域的维纳滤波的重建结果
Fig. 17. Puppet model with arms up and reconstruction results of NLOS imaging based on mid-frequency Wiener filtering.
图 18 传统维纳滤波的重建结果与基于中频域的维纳滤波的重建结果对比 (a)−(f)人偶模型手臂向上的隐藏场景分别取K为0.01, 0.1, 1, 10, 100, 1000进行维纳滤波复原的结果; (h)人偶模型手臂向上隐藏场景基于中频域的维纳滤波重建的结果, 估出的K为1.5939
Fig. 18. Comparison between the reconstruction results of traditional Wiener filtering and the reconstruction results based on Wiener filtering in the mid-frequency domain: (a)−(f) The results of Wiener filtering reconstruction with K as 0.01, 0.1, 1, 10, 100, and 1000 for puppet model with arms up respectively; (h) the reconstruction result of puppet model with arms up using the NLOS imaging algorithm based on Wiener filtering of mid-frequency domain, and the estimated K is 1.5939.
图 16 传统维纳滤波的重建结果与基于中频域的维纳滤波的重建结果对比 (a)−(f) C形纸板的隐藏场景分别取K为0.01, 0.1, 1, 10, 100, 1000进行维纳滤波复原的结果; (h) C形纸板隐藏场景基于中频域的维纳滤波重建的结果, 估出K值为0.8096
Fig. 16. Comparison between the reconstruction results of traditional Wiener filtering and the reconstruction results based on Wiener filtering in the mid-frequency domain: (a)−(f) The results of Wiener filtering reconstruction with K as 0.01, 0.1, 1, 10, 100, and 1000 for C-shaped cardboard respectively; (h) the reconstruction result of C- shaped cardboard using the NLOS imaging algorithm based on Wiener filtering of mid-frequency domain, and the estimated K is 0.8096.
图 19 重建图像综合质量评价, 其中蓝色线为设置不同K得到的重建图像的综合质量评价值, 红色圆圈为基于中频域的维纳滤波重建图像的综合质量评价值 (a) T形纸板; (b)人偶模型手臂向下; (c)房屋形纸板; (d) C形纸板; (e)人偶模型手臂向上
Fig. 19. Comprehensive quality evaluation of reconstructed images, the blue line is the comprehensive quality evaluation value of the reconstructed image obtained by setting different K, and the red circle is the comprehensive quality evaluation value of the reconstructed image based on the Wiener filter in the intermediate frequency domain: (a) The Eval of T-shaped cardboard, (b) the Eval of puppet model with arms down, (c) the Eval of house-shaped cardboard, (d) the Eval of C-shaped cardboard, (e) the Eval of puppet model with arms up.
-
[1] Laurenzis M, Velten A 2014 J. Electron. Imaging 23 063003
Google Scholar
[2] Chan S, Warburton R E, Gariepy G, Leach J, Faccio D 2017 Opt. Express 25 10109
Google Scholar
[3] Bouman K L, Ye V, Yedidia A B, Durand F, Wornell G W, Torralba A, Freeman W T 2017 Proceedings of the IEEE International Conference on Computer Vision Venice, Italy, October 22–29, 2017 pp2270–2278
[4] Musarra G, Lyons A, Conca E, Altmann Y, Villa F, Zappa F, Padgett M J, Faccio D 2019 Phys. Rev. Appl. 12 011002
Google Scholar
[5] Liu X C, Guillén I, La Manna M, Nam J H, Reza S A, Huu Le T, Jarabo A, Gutierrez D, Velten A 2019 Nature 572 620
Google Scholar
[6] Xin S, Nousias S, Kutulakos K N, et al. 2019 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Long Beach, CA, USA, June 15–20, 2019 pp6800–6809
[7] Wang B, Zheng M Y, Han J J, Huang X, Xie X P, Xu F H, Zhang Q, Pan J W 2021 Phys. Rev. Lett. 127 053602
Google Scholar
[8] Kirmani A, Hutchison T, Davis J, Raskar R 2009 2009 IEEE 12 th International Conference on Computer Vision Kyoto, Japan, September 29–Octorber 2, 2009 pp159–166
[9] Velten A, Willwacher T, Gupta O, Veeraraghavan A, Bawendi M G, Raskar R 2012 Nat. Commun. 3 1
[10] Klein J, Laurenzis M, Hullin M 2016 Electro-Optical Remote Sensing X Edinburgh, UK, September 26–29, 2016 p998802
[11] O’Toole M, Lindell D B, Wetzstein G 2018 Nature 555 338
Google Scholar
[12] 任禹, 罗一涵, 徐少雄, 马浩统, 谭毅 2021 光电工程 48 200124
Ren Y, Luo Y H, Xu S X, Ma H T, Tan Y 2021 Opto-Electron. Eng. 48 200124 (in Chinese)
[13] Jin C F, Xie J H, Zhang S Q, Zhang Z, Zhao Y 2018 Opt. Express 26 20089
Google Scholar
[14] Arellano V, Gutierrez D, Jarabo A 2017 Opt. Express 25 11574
Google Scholar
[15] Wu C, Liu J J, Huang X, Li Z P, Yu C, Ye J T, Zhang J, Zhang Q, Dou X K, Goyal V K 2021 P. Natl. Acad. Sci. 118 e2024468118
Google Scholar
[16] Satat G, Tancik M, Gupta O, Heshmat B, Raskar R 2017 Opt. Express 25 17466
Google Scholar
[17] Caramazza P, Boccolini A, Buschek D, Hullin M, Higham C F, Henderson R, Murray-Smith R, Faccio D 2018 Sci. Rep-uk. 8 1
[18] Musarra G, Caramazza P, Turpin A, Lyons A, Higham C F, Murray-Smith R, Faccio D 2019 Advanced Photon Counting Techniques XIII Baltimore, Maryland, United States, May 13, 2019 p1097803
[19] Isogawa M, Yuan Y, O'Toole M, Kitani K M 2020 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Seattle, WA, USA, June 13–19, 2020 pp7013–7022
[20] Gariepy G, Tonolini F, Henderson R, Leach J, Faccio D 2016 Nat. Photonics 10 23
Google Scholar
[21] Hullin M B 2014 Optoelectronic Imaging and Multimedia Technology III Beijing, China, October 29, 2014 pp197–204
[22] Luo Y H, Fu C Y 2011 Opt Eng 50 047004
Google Scholar
[23] 许丽娜, 肖奇, 何鲁晓 2019 武汉大学学报(信息科学版) 44 546
Xu L N, Xiao Q, He L X 2019 Geomat. Inf. Sci. Wuhan Univ. 44 546
下载:
计量
- 文章访问数: 3336
- PDF下载量: 62
- 被引次数: 0
