-
基于摄动理论和广义伯努利方程, 推导出单气泡在超声场中径向振动方程、平移方程和气泡形变方程. 数值计算这3个方程, 可以得到气泡半径、气泡中心的位移和气泡形变随时间的演化图. 计算结果表明: 当气泡初始半径和驱动声压不变时, 气泡中心初始平移速度增大, 气泡径向振动几乎不变, 但气泡中心位移和形变量增大, 气泡非球形振动愈加明显. 当初始平移速度比较小时, 气泡的
${R_{0}}\text {-}p_{\rm a}$ 相图中, 不稳定区域仅集中在高驱动声压区域. 随着气泡中心初始平移速度不断增大, 半径和驱动声压均较小的区域开始呈现不稳定性, 且整体不稳定空间范围逐渐增大. 另外, 气泡在声驻波场中不同位置呈现出不同的振动特征. 离波腹点越近的气泡, 其径向振动幅度越大, 但气泡的平移和形变量变化很小,${R_{0}}\text {-} p_{\rm a}$ 相图中不稳定性区域平面分数之间的误差小于4%.Based on the perturbation theory and generalized Bernoulli equation, the equations describing the radius, translation and deformation of a single gas bubble in ultrasonic field are derived. The evolutions of the radius, displacement and deformation of the bubble with time can be obtained by numerically calculating these equations. The calculation results show that when the initial radius of the bubble and the driving pressure both keep constant, the displacement and shape variable of the bubble increase with the augment of the initial translational velocity of the bubble’s center, and the non-spherical vibration of the bubble becomes more intense. However, the radial vibration of the bubble almost remains unchanged. When the initial translation velocity of the bubble is relatively small, the unstable region is concentrated only in the region of high driving sound pressure in the$R_{0}\text-p_{\rm a}$ phase diagram of the bubble. As the initial translational velocity increases, the region with small radius and driving sound pressure begins to show instability, and the overall unstable region gradually increases. In addition, a bubble presents different vibration characteristics at different positions in the acoustic standing wave field. The closer to the antinode of sound wave the bubble is, the greater the radial amplitude of the bubble’s vibration is. However, the variable of the translation and shape of the bubble are very small. The error between the plane fractions of the unstable region in the phase diagram of$R_{0}\text{-} p_ {\rm a}$ is less than 4%.-
Keywords:
- caviation bubble /
- translation /
- non-spherical oscillation /
- instability
[1] Leighton T G 1977 The Acoustic Bubble (San Diego: Academic Press) p72
[2] Frenzel H, Schultes H 1934 Z. Phys. Chem. Abt. B 27 421
Google Scholar
[3] Niemczewski B 2014 Ultrason. Sonochem. 21 354
Google Scholar
[4] Oshima R, Yamamoto T A, Mizukoshi Y, Nagata Y, Maeda Y 1999 Nanostruct. Mater. 12 111
Google Scholar
[5] Hussein E M, Khairou K S 2014 Rev. J. Chem. 4 221
Google Scholar
[6] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[7] Plesset M S 1954 J. Appl. Phys. 25 96
Google Scholar
[8] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[9] Hilgenfeldt S, Lohse D, Brenner M P 1996 Phys. Fluids 8 2808
Google Scholar
[10] An Y, Lu T, Yang B 2005 Phys. Rev. E 71 026310
Google Scholar
[11] Zhang W J, An Y 2013 Phys. Rev. E 87 053023
Google Scholar
[12] Liang J F, Chen W Z, Shao W H, Qi S B 2012 Chin. Phys. Lett. 29 074701
Google Scholar
[13] Liang J F, Wang X, Yang J, Gong L X 2017 Ultrasonics 75 58
Google Scholar
[14] Madrazo A, García N, Nieto-Vesperinas M 1998 Phys. Rev. Lett. 80 4590
Google Scholar
[15] Barbat T, Ashgriz N, Liu C S 1999 J. Fluid Mech. 389 137
Google Scholar
[16] Flannigan D J, Suslick K S 2007 Phys. Rev. Lett. 99 134301
Google Scholar
[17] Cui W C, Chen W Z, Qi S B, Zhou C, Tu J 2012 J. Acoust. Soc. Am. 132 138
Google Scholar
[18] Wu W H, Yang P F, Zhai W, Wei B B 2019 Chin. Phys. Lett. 36 084302
Google Scholar
[19] Wu W H, Eskin D G, Priyadarshi A, Subroto T, Tzanakis I, Zhai W 2021 Ultrason. Sonochem. 73 105501
Google Scholar
[20] Doinikov A A 2001 Phys. Rev. E 64 026301
Google Scholar
[21] Doinikov A A 2002 Phys. Fluids 14 1420
Google Scholar
[22] 沈壮 志 2015 64 124702
Google Scholar
Shen Z Z 2015 Acta Phys. Sin. 64 124702
Google Scholar
[23] 马艳, 林书玉, 徐洁 2018 67 034301
Google Scholar
Ma Y, Lin S Y, Xu J 2018 Acta Phys. Sin. 67 034301
Google Scholar
[24] Zhang L L, Chen W Z, Zhang Y Y, Wu Y R, Wang X, Zhao G Y 2020 Chin. Phys. B 29 034303
Google Scholar
[25] Feng Z C, Leal L G 1995 Phys. Fluids 7 1325
Google Scholar
[26] Reddy A J, Szeri A J 2002 Phys. Fluids 14 2216
Google Scholar
[27] Doinikov A A 2004 J. Fluid Mech. 501 1
Google Scholar
[28] Mettin R, Doinikov A A 2009 Appl. Acoust. 70 1330
Google Scholar
[29] 刘式适, 刘式达 2002 特殊函数 (第二版) (北京: 气象出版社) 第255, 237−240, 247−251页
Liu S S, Liu S D 2002 Special Function (2nd Ed.) (Beijing: Qixiang Press) pp255, 237−240, 247−251 (in Chinese)
[30] Franc J P, Michel J M 2004 Fundamentals of Cavitation (Nether- lands: Kluwer Academic Publisher) p341
[31] Plesset M S 1949 J. Appl. Mech. 16 277
Google Scholar
[32] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第250−253页
Chen W Z 2014 Physics of Acoustic Cavitation (Beijing: Science Press) pp250−253 (in Chinese)
[33] Tsiglifis K, Pelekasi N A 2005 Phys. Fluids 17 102101
Google Scholar
[34] Kostas T, Pelekasis N A 2007 Ultrason. Sonochem. 14 456
Google Scholar
-
图 1 含有气泡脉动、平移和形变的几何图形
Fig. 1. Geometry for single bubble with pulsation, translation and shape perturbation.
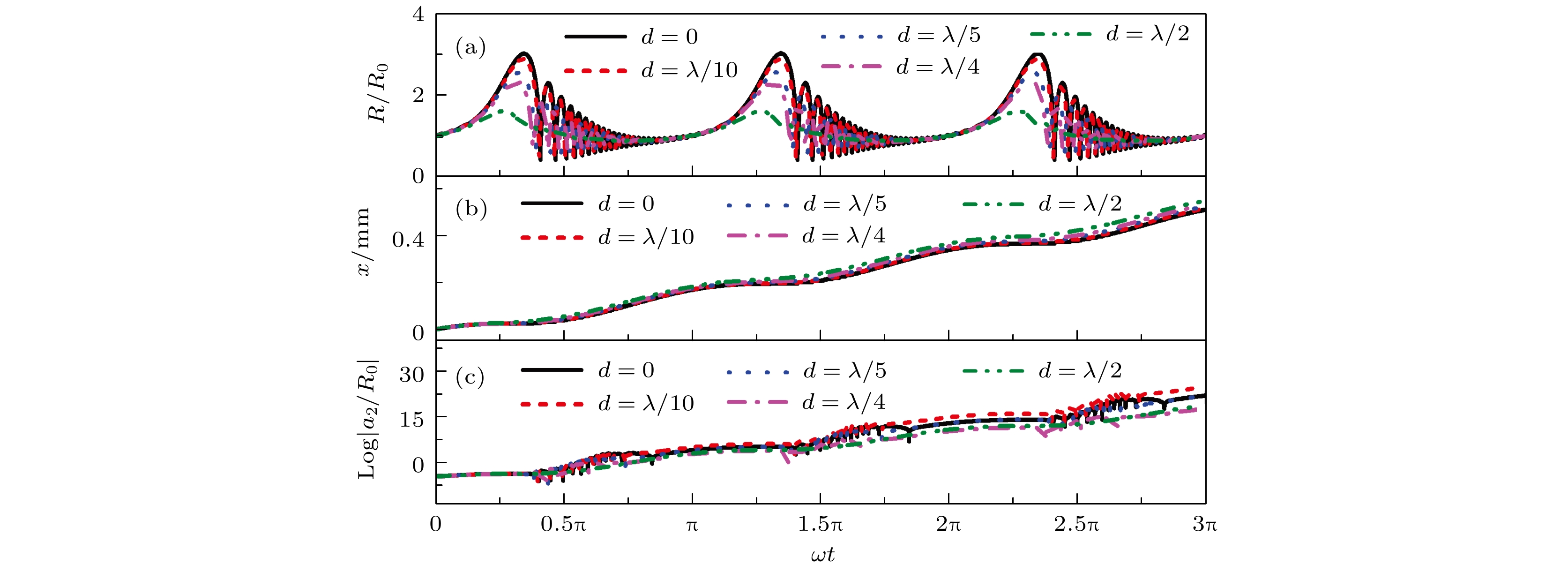
图 2 不同初始平移速度
$v_{x0}$ 下, (a)气泡径向半径、(b)气泡中心平移以及(c)气泡表面形变随时间的演化.$R_{0}$ = 4.5 µm,$p_{\rm a}$ = 1.15 × 105 PaFig. 2. Evolutions of (a) radius, (b) translation and (c) deformation with time for a cavitation bubble with different initial translational velocity (
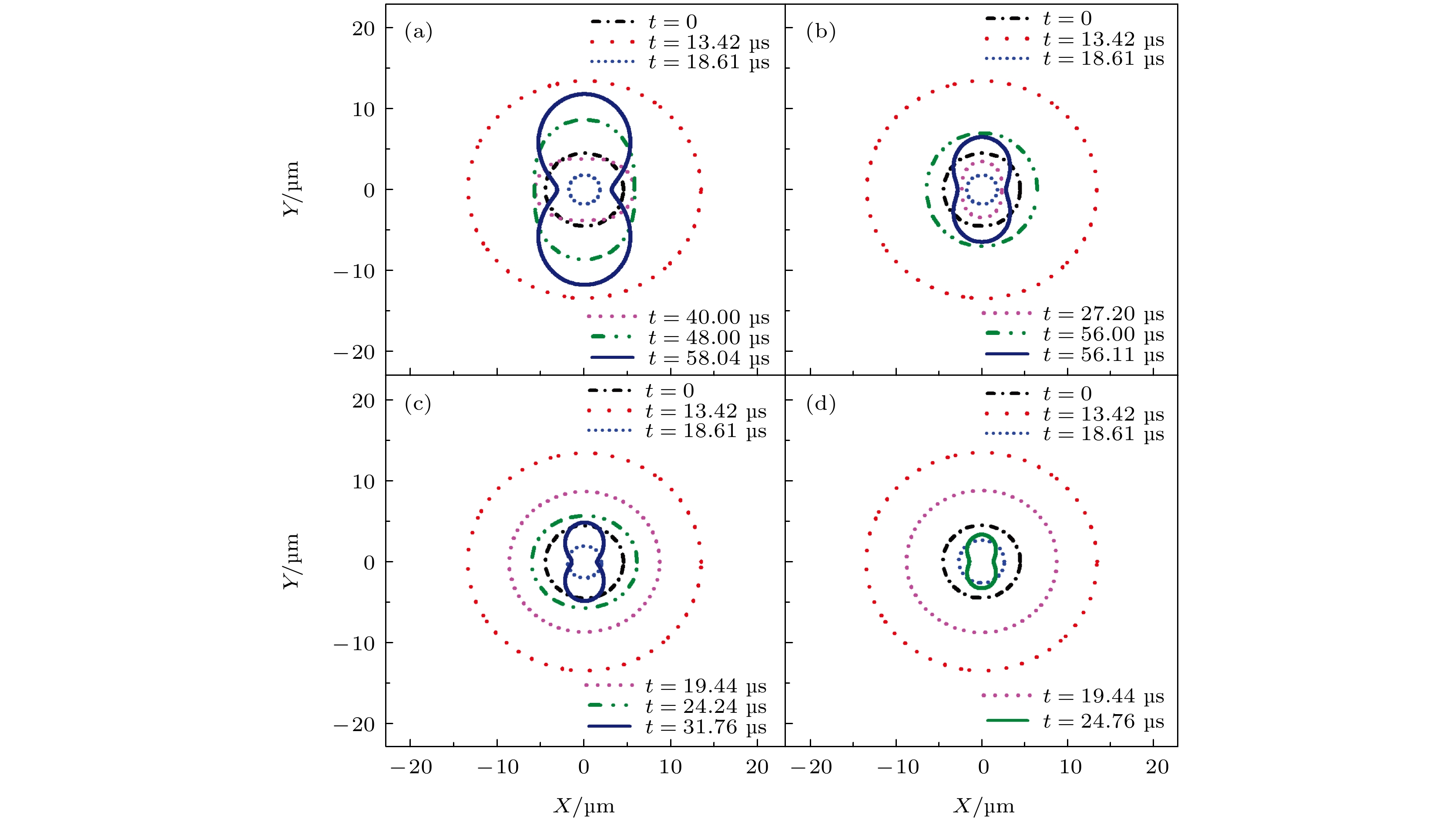
$v_{x0}$ ), respectively.$R_{0}$ = 4.5 µm,$p_{\rm a}$ = 1.15 × 105 Pa
图 3 不同初始平移速度条件下, 不同时刻气泡振动的形状 (a)
$v_{x0}$ = 0; (b)$v_{x0}$ = 1 m/s; (c)$v_{x0}$ = 3 m/s; (d)$v_{x0}$ = 5 m/s. 其中$R_{0}$ = 4.5 µm,$p_{\rm a}$ = 1.15 × 105 PaFig. 3. Simulations of shapes of a gas bubble’s oscillation at different times under different initial translational velocity: (a)
$v_{x0}$ = 0; (b)$v_{x0}$ = 1 m/s; (c)$v_{x0}$ = 3 m/s; (d)$v_{x0}$ = 5 m/s.$R_{0}$ = 4.5 µm,$p_{\rm a}$ = 1.15 × 105 Pa
图 4 不同初始平移速度下, 气泡的
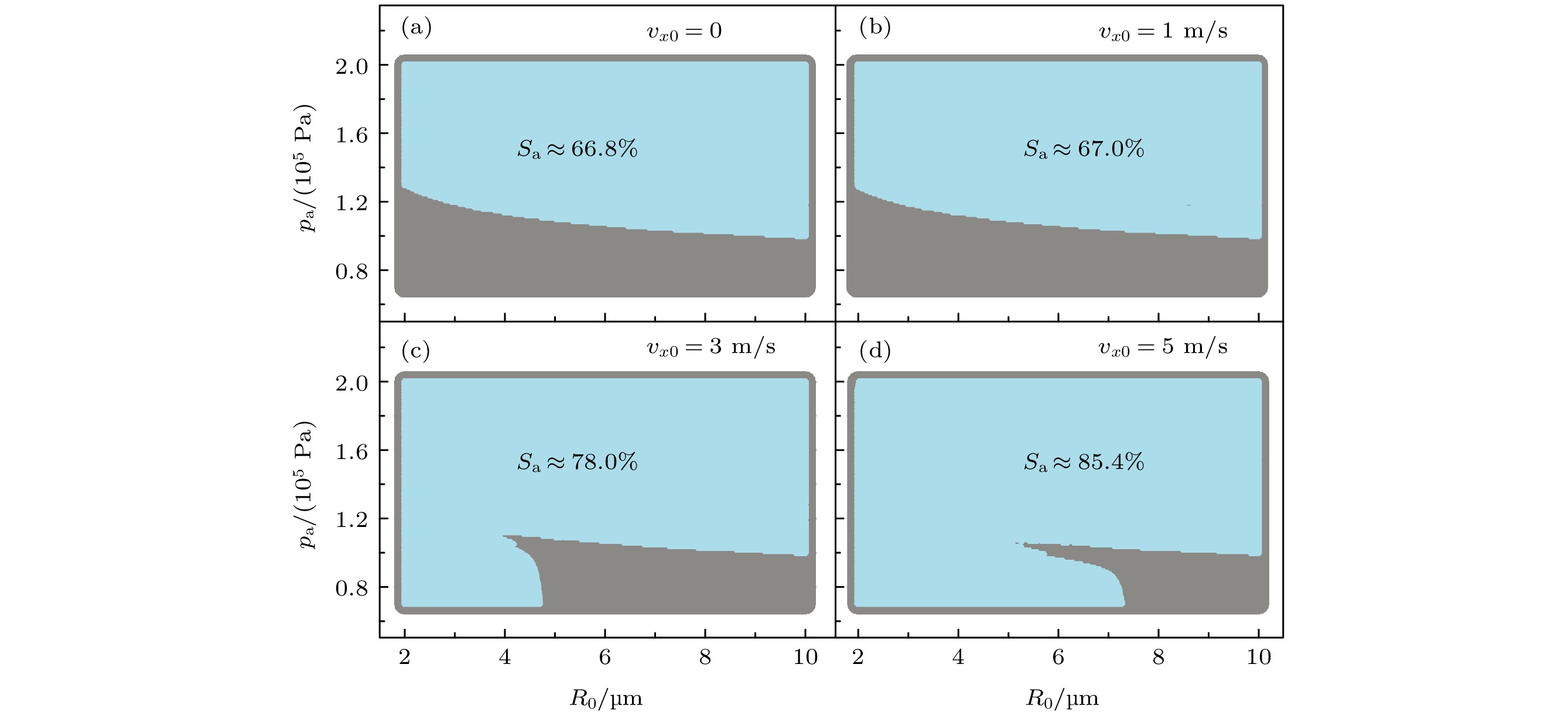
${R_{0}}\text {-}$ $p_{\rm a}$ 相图 (a)$v_{x0}$ = 0; (b)$v_{x0}$ = 1 m/s; (c)$v_{x0}$ = 3 m/s; (d)$v_{x0}$ = 5 m/s.$p_{\rm a}= $ $ 1.15$ × 105 Pa,$R_{0}$ = 4.5 µmFig. 4.
${R_{0}}\text {-}$ $p_{\rm a}$ phase diagram of a gas bubble under different initial translational velocity: (a)$v_{x0}$ = 0; (b)$v_{x0}$ = 1 m/s; (c)$v_{x0}$ = 3 m/s; (d)$v_{x0}$ = 5 m/s.$p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm
图 5 不同位置处, 气泡半径、平移位移和形变随时间的演化图像(
$p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm,$v_{x0}$ = 5 m/s)Fig. 5. Evolution of bubble’s radius, translation and deformation at different distance d from the antinodal point of acoustical wave.
$p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm,$v_{x0}$ = 5 m/s.
图 6 不同位置处, 不同时刻气泡振动的形状(
$p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm,$v_{x0}$ = 5 m/s) (a) d = 0; (b) d = λ/5; (c) d = λ/4; (d) d = λ/2Fig. 6. Simulations of shapes of a gas bubble’s oscillation at different times at different distances from the antinodal of acoustical wave: (a) d = 0; (b) d = λ/5; (c) d = λ/4; (d) d = λ/2.
$p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm,$v_{x0}$ = 5 m/s.
图 7 不同位置处, 气泡的
$R_{0}$ -$p_{\rm a}$ 相图($p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm,$v_{x0}$ = 5 m/s) (a) d = 0; (b) d = λ/5; (c) d = λ/4; (d) d = λ/2Fig. 7.
$R_{0}$ -$p_{\rm a}$ phase diagrams of a gas bubble at different distances from the antinodal of acoustical wave: (a) d = 0; (b) d = λ/5; (c) d = λ/4; (d) d = λ/2.$p_{\rm a}=1.15$ × 105 Pa,$R_{0}$ = 4.5 µm,$v_{x0}$ = 5 m/s.表 1 数值计算中使用的物理量参数
Table 1. Physical parameters used in the numerical calculation.
物理量 单位 数值 液体密度ρ kg/m3 1000 液体中声速c m/s 1481 液体表面张力系数σ N/m 0.072 液体粘度系数η Pa·s 0.001 超声频率f Hz 2.5 × 104 气泡内初始压强$ p_{0}$ Pa 1.013 × 105 环境压强$ p_{\infty}$ Pa 1.013 × 105 绝热指数γ 1.4 
下载: 导出CSV
-
[1] Leighton T G 1977 The Acoustic Bubble (San Diego: Academic Press) p72
[2] Frenzel H, Schultes H 1934 Z. Phys. Chem. Abt. B 27 421
Google Scholar
[3] Niemczewski B 2014 Ultrason. Sonochem. 21 354
Google Scholar
[4] Oshima R, Yamamoto T A, Mizukoshi Y, Nagata Y, Maeda Y 1999 Nanostruct. Mater. 12 111
Google Scholar
[5] Hussein E M, Khairou K S 2014 Rev. J. Chem. 4 221
Google Scholar
[6] Rayleigh L 1917 Philos. Mag. 34 94
Google Scholar
[7] Plesset M S 1954 J. Appl. Phys. 25 96
Google Scholar
[8] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[9] Hilgenfeldt S, Lohse D, Brenner M P 1996 Phys. Fluids 8 2808
Google Scholar
[10] An Y, Lu T, Yang B 2005 Phys. Rev. E 71 026310
Google Scholar
[11] Zhang W J, An Y 2013 Phys. Rev. E 87 053023
Google Scholar
[12] Liang J F, Chen W Z, Shao W H, Qi S B 2012 Chin. Phys. Lett. 29 074701
Google Scholar
[13] Liang J F, Wang X, Yang J, Gong L X 2017 Ultrasonics 75 58
Google Scholar
[14] Madrazo A, García N, Nieto-Vesperinas M 1998 Phys. Rev. Lett. 80 4590
Google Scholar
[15] Barbat T, Ashgriz N, Liu C S 1999 J. Fluid Mech. 389 137
Google Scholar
[16] Flannigan D J, Suslick K S 2007 Phys. Rev. Lett. 99 134301
Google Scholar
[17] Cui W C, Chen W Z, Qi S B, Zhou C, Tu J 2012 J. Acoust. Soc. Am. 132 138
Google Scholar
[18] Wu W H, Yang P F, Zhai W, Wei B B 2019 Chin. Phys. Lett. 36 084302
Google Scholar
[19] Wu W H, Eskin D G, Priyadarshi A, Subroto T, Tzanakis I, Zhai W 2021 Ultrason. Sonochem. 73 105501
Google Scholar
[20] Doinikov A A 2001 Phys. Rev. E 64 026301
Google Scholar
[21] Doinikov A A 2002 Phys. Fluids 14 1420
Google Scholar
[22] 沈壮 志 2015 64 124702
Google Scholar
Shen Z Z 2015 Acta Phys. Sin. 64 124702
Google Scholar
[23] 马艳, 林书玉, 徐洁 2018 67 034301
Google Scholar
Ma Y, Lin S Y, Xu J 2018 Acta Phys. Sin. 67 034301
Google Scholar
[24] Zhang L L, Chen W Z, Zhang Y Y, Wu Y R, Wang X, Zhao G Y 2020 Chin. Phys. B 29 034303
Google Scholar
[25] Feng Z C, Leal L G 1995 Phys. Fluids 7 1325
Google Scholar
[26] Reddy A J, Szeri A J 2002 Phys. Fluids 14 2216
Google Scholar
[27] Doinikov A A 2004 J. Fluid Mech. 501 1
Google Scholar
[28] Mettin R, Doinikov A A 2009 Appl. Acoust. 70 1330
Google Scholar
[29] 刘式适, 刘式达 2002 特殊函数 (第二版) (北京: 气象出版社) 第255, 237−240, 247−251页
Liu S S, Liu S D 2002 Special Function (2nd Ed.) (Beijing: Qixiang Press) pp255, 237−240, 247−251 (in Chinese)
[30] Franc J P, Michel J M 2004 Fundamentals of Cavitation (Nether- lands: Kluwer Academic Publisher) p341
[31] Plesset M S 1949 J. Appl. Mech. 16 277
Google Scholar
[32] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第250−253页
Chen W Z 2014 Physics of Acoustic Cavitation (Beijing: Science Press) pp250−253 (in Chinese)
[33] Tsiglifis K, Pelekasi N A 2005 Phys. Fluids 17 102101
Google Scholar
[34] Kostas T, Pelekasis N A 2007 Ultrason. Sonochem. 14 456
Google Scholar
下载:
计量
- 文章访问数: 4157
- PDF下载量: 117
- 被引次数: 0
