-
Rydberg原子在微波和太赫兹频段具有极大的电偶极矩, 利用量子干涉效应可实现对该频段电磁波场强的高灵敏探测, 理论上灵敏度可达到远高于现有探测技术的水平. 基于Rydberg原子量子效应的电磁场探测及精密测量技术在太赫兹的场强和功率计量、太赫兹通信和太赫兹成像等方面有着巨大的应用前景. 本文回顾了基于Rydberg原子量子干涉效应实现电磁波电场自校准和可溯源测量的基本理论和实验技术, 详细介绍了基于Rydberg原子的高灵敏太赫兹场强测量、太赫兹近场高速成像和太赫兹数字通信的基本原理和技术方案. 最后简单介绍了本研究团队正在开展的基于Rydberg原子的太赫兹探测工作.Rydberg atoms have large electric dipole moments in the microwave and terahertz frequency band. The detection of electromagnetic field intensity in this frequency band can be achieved by using quantum interference effects. Theoretically, this detection method can have a sensitivity much higher than the traditional detection methods. Therefore, electromagnetic field detection and precision measurement technology based on Rydberg atomic quantum effects has great application prospects in terahertz field strength and power measurement, terahertz communication and imaging. In this paper, we review the basic theory and experimental methods to realize the self-calibration and traceability measurement of electromagnetic field based on Rydberg atomic quantum effects. The principle and technical scheme of high-sensitivity terahertz field strength measurement, terahertz near-field high-speed imaging and terahertz digital communication based on Rydberg atom are introduced in detail. Finally, the processing terahertz detection work based on Rydberg atom by our research team is also mentioned briefly.
-
Keywords:
- Rydberg atom /
- precise measurement of electromagnetic field /
- terahertz imaging /
- terahertz communication
[1] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press) pp38−49
[2] Sedlacek J A, Schwettmann A, Kübler H, Low R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
Google Scholar
[3] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
Google Scholar
[4] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003
Google Scholar
[5] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
Google Scholar
[6] Fan H Q, Kumar S, Daschner R, Kübler H, Shaffer J P 2014 Opt. Lett. 39 3030
Google Scholar
[7] Holloway C L, Gordon J A, Jeerts S, Schwarzkopf A, Anderson D A, Miller S A, Thaicharoen N, Raithel G 2014 IEEE Trans. Antenn. Propag. 62 6169
Google Scholar
[8] Gordon J A, Holloway C L, Schwarzkopf A, Anderson D A, Miller S, Thaicharoen N, Raithel G 2014 Appl. Phys. Lett. 105 024104
Google Scholar
[9] Holloway C L, Gordon J A, Schwarzkopf A, Anderson D A, Miller S A, Thaicharoen N, Raithel G 2014 Appl. Phys. Lett. 104 244102
Google Scholar
[10] Fan H Q, Kumar S, Sheng J T, Shaffer J P 2015 Phys. Rev. Appl. 4 044015
Google Scholar
[11] Fan H Q, Kumar S, Kübler H, Shaffer J P 2016 J. Phys. B 49 104004
Google Scholar
[12] Kumar S, Fan H Q, Kübler H, Jahangiri A J, Shaffer J P 2017 Opt. Express 25 8625
Google Scholar
[13] Kumar S, Fan H Q, Kübler H, Sheng J T, Shaffer J P 2017 Sci. Rep. 7 42981
Google Scholar
[14] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030
Google Scholar
[15] Song Z F, Liu H P, Liu X C, Zhang W F, Zou H Y, Zhang J, Qu J F 2019 Opt. Express 27 8848
Google Scholar
[16] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[17] Liao K Y, Tu H T, Yang S Z, Chen C J, Liu X H, Liang J, Zhang X D, Yan H, Zhu S L 2020 Phys. Rev. A 101 053432
Google Scholar
[18] Hafez H A, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, Ozaki T 2016 J. Opt. 18 093004
Google Scholar
[19] Holloway C L, Simons M T, Haddab A H, Gordon J A, Anderson D A, Raithel G, Voran S D 2020 IEEE Antennas Propag. Mag.
Google Scholar
[20] 黄巍, 梁振涛, 杜炎雄, 颜辉, 朱诗亮 2015 64 160702
Google Scholar
Huang W, Liang Z T, Du Y X, Yan H, Zhu S L 2015 Acta Phys. Sin. 64 160702
Google Scholar
[21] 焦月春, 赵建明, 贾锁堂 2018 67 073201
Google Scholar
Jiao Y C, Zhao J M, Jia S T 2018 Acta Phys. Sin. 67 073201
Google Scholar
[22] Wade C G 2018 Terahertz Wave Detection and Imaging with a Hot Rydberg Vapour (Switzerland: Springer Theses) pp55−63
[23] Hughes I, Hase T 2010 Measurements and Their Uncertainties (Oxford: Oxford University Press) pp74−83
[24] Šibalić N, Pritchard J D, Adams C S, Weatherill K J 2017 Comput. Phys. Commun. 220 319
Google Scholar
[25] Raimond J M, Goy P, Vitrant G, Haroche S 1981 J. Phys. Colloques 42 C8-37
Google Scholar
[26] Drabbels M, Noordam L D 1999 Appl. Phys. Lett. 74 1797
Google Scholar
[27] Gurtler A, Meijer A S, Van der Zande W J 2003 Appl. Phys. Lett. 83 222
Google Scholar
[28] Wade C G, Šibalić N, De Melo N R, Kondo J M, Adams C S, Weatherill K J 2016 Nat. Photonics 11 40
Google Scholar
[29] Mitrofanov O, Tan T, Mark P R, Bowden B, Harrington J A 2009 Appl. Phys. Lett. 94 171104
Google Scholar
[30] Bitzer A, Walther M 2008 Appl. Phys. Lett. 92 231101
Google Scholar
[31] Seo M A, Adam A J L, Kang J H, Lee J W, Jeoung S C, Park Q H, Planken P C M, Kim D S 2007 Opt. Express 15 11781
Google Scholar
[32] Downes L A, MacKellar A T, Whiting D J, Bourgenot C, Adams C S, Weatherill K J 2020 Phys. Rev. X 10 011027
Google Scholar
[33] Jansen C, Wietzke S, Peters O, Scheller M, Vieweg N, Salhi M, Krumbholz N, Jrdens C, Hochrein T, Koch M 2010 Appl. Opt. 49 E48
Google Scholar
[34] Jepsen P, Cooke D, Koch M 2011 Laser Photonics Rev. 5 124
Google Scholar
[35] Mittleman D M 2018 Opt. Express 26 9417
Google Scholar
[36] Hanzo L, Webb W T, keller T 2000 Single- and Multi-carrier Quadrature Amplitude Modulation: Principles and Applications for Personal Communications, WATM and Broadcasting (2nd Ed.) (Southampton: Wiley-IEEE Press) pp23−56
[37] Meyer D H, Cox K C, Fatemi F K, Kunz P D 2018 Appl. Phys. Lett. 112 211108
Google Scholar
-
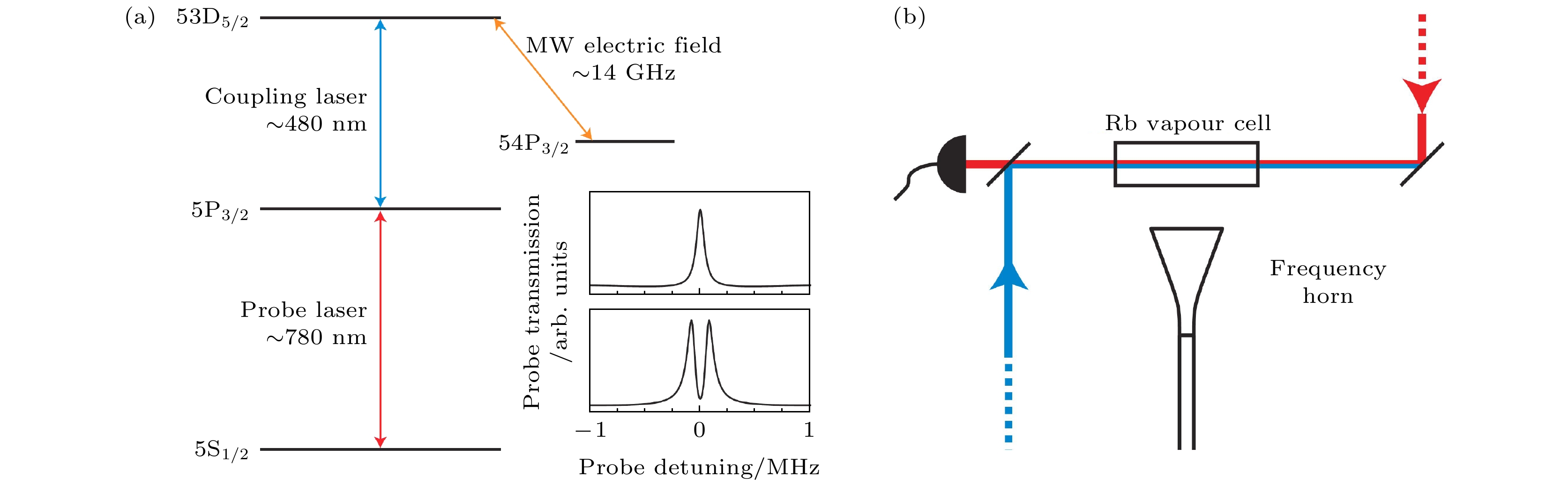
图 1 (a) Rydberg原子量子干涉法测量微波电场强度能级示意图, 以及微波场作用前后探测光透射峰(中下); (b) 实验测量装置图[2]
Fig. 1. (a) Energy level diagram for the four-level system. The top part of the inset shows an example EIT feature without a microwave electric field. The bottom part of the inset shows an example EIT-AT with a microwave electric field. (b) Experimental set-up used for the experiments[2].
图 2 电磁波光谱(太赫兹区域介于微波与红外之间)
Fig. 2. Electromagnetic spectrum (terahertz region between microwave and infrared).
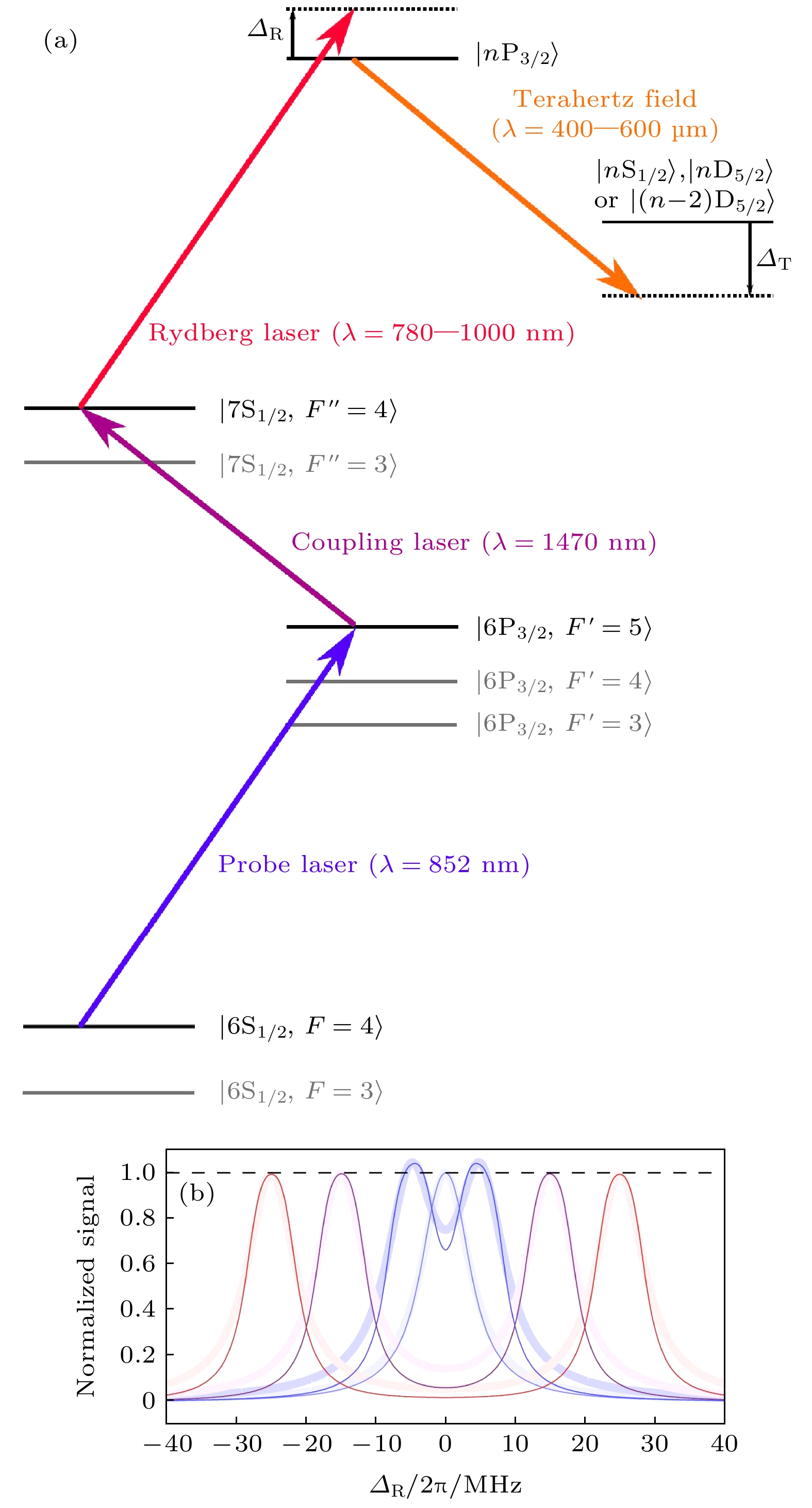
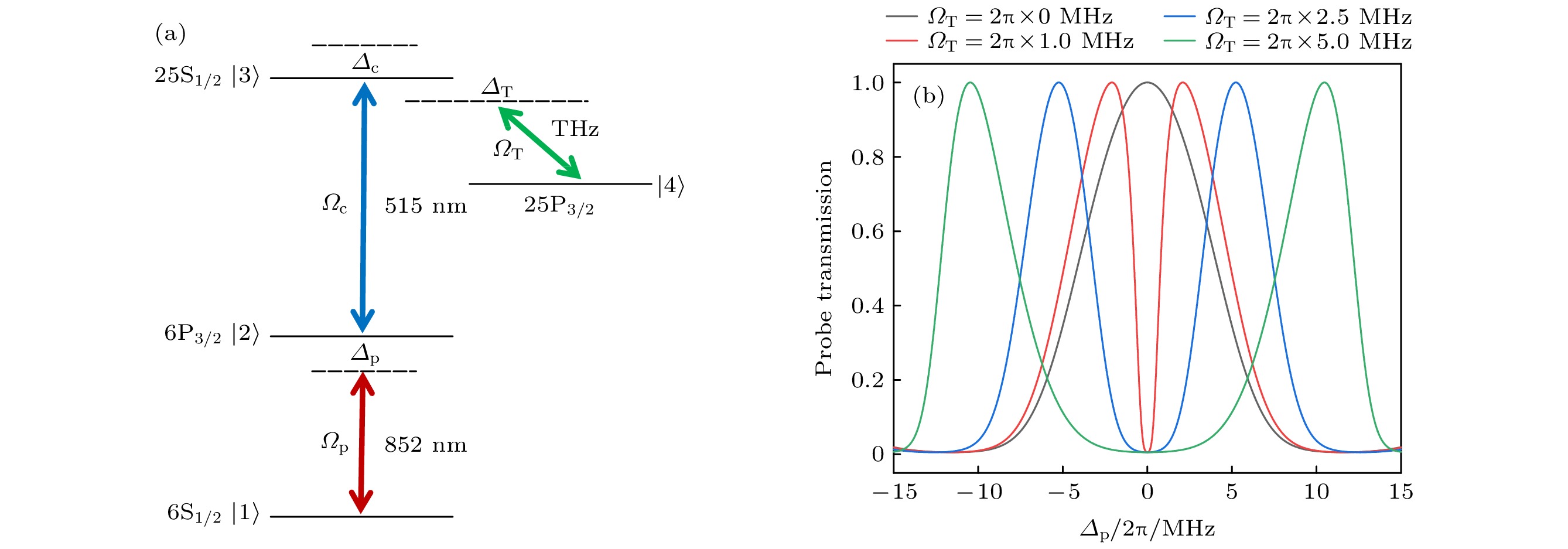
图 3 (a) Cs Rydberg态三步激发能级图; (b) 当
$\varOmega_{\rm{p}} = \varOmega_{\rm{c}} = $ $ 2 {\text {π}} \times5$ MHz,$ \varOmega_{\rm{R}} = 2 {\text {π}}\times8.4 $ MHz,$\varOmega_{\rm{T}} = 2 {\text {π}} \times[0,\;10,\;30, $ $ 50]$ MHz时, 利用5能级光学布洛赫模型拟合Rydberg EIT-AT分裂(彩实线)及对应的洛伦兹线性拟合(阴影线)[22]Fig. 3. (a) Three step ladder excitation scheme (Rydberg states in caesium); (b) when
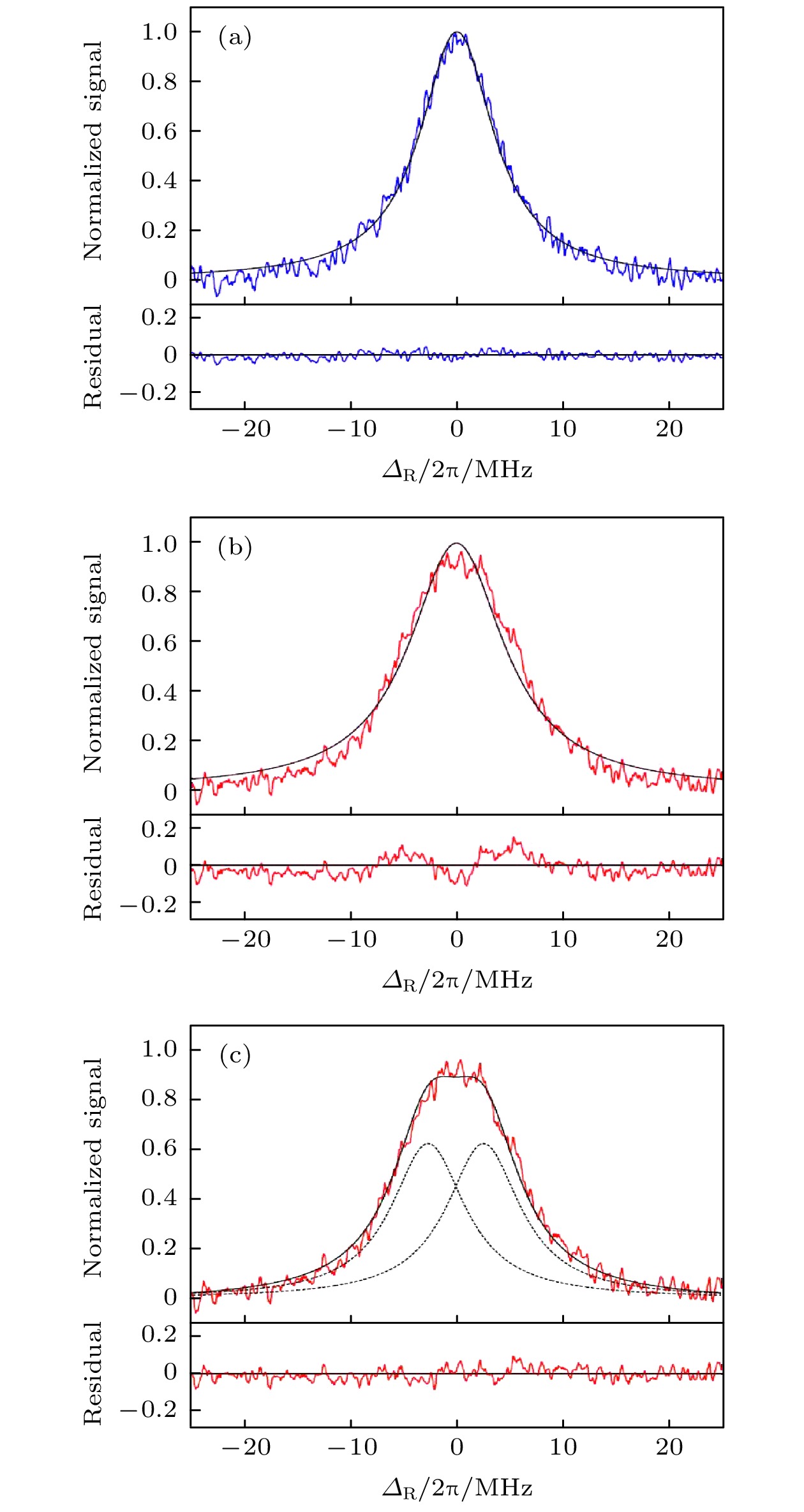
$ \varOmega_{\rm{p}} = \varOmega_{\rm{c}} = 2 {\text {π}} \times5 $ MHz,$ \varOmega_{\rm{R}} = 2 {\text {π}} \times8.4 $ MHz,$ \varOmega_{\rm{T}} = 2 {\text {π}} \times[0,\; 10,\;30,\;50]$ MHz, Autler-Townes splitting simulation for a 5-level optical Bloch model (coloured lines) with Lorenzian features (shaded lines)[22].
图 4 基于Rydberg EIT的THz场强测量 (a) 当
$ \varOmega_{\rm{T}} = 0 $ 时, 使用单洛伦兹线性拟合EIT透射峰; (b) 当$\varOmega_{\rm{T}}/2 {\text {π}}= $ $ (5.2 \pm 1.4)$ MHz时, 使用单洛伦兹线性拟合EIT-AT 分裂峰; (c) 当$\varOmega_{\rm{T}}/2 {\text {π}}= (5.2 \pm 1.4)$ MHz时, 使用双洛伦兹线性拟合EIT-AT分裂峰; 下方数据为各自对应的拟合残差[22]Fig. 4. THz electric field amplitude measurement: (a) Probe transmission line shape for
$ \varOmega_{\rm{T}} = 0 $ and best fit line (dashed) is a single Lorentzian; (b) probe transmission line shape for$\varOmega_{\rm{T}}/2 {\text {π}}= (5.2 \pm 1.4)$ MHz and best fit line (dashed) is a single Lorentzian; (c) probe transmission line shape for$\varOmega_{\rm{T}}/2 {\text {π}} = (5.2 \pm 1.4)$ MHz and a summed pair of Lorentzian peaks. Below datas are residuals for different models[22].
图 5 基于Rydberg原子太赫兹近场成像 (a) 实验系统装置; (b) 太赫兹荧光成像; (c) Rydberg原子在THz波段下共振跃迁频率对应的跃迁偶极矩; (d) 铯原子能级激发图; (e) 录制的视频[28]
Fig. 5. Real-time near-field THz imaging based on Rydberg atom: (a) Experimental layout; (b) spatially resolved THz intensity; (c) resonant transitions between Rydberg states in the THz band; (d) caesium atomic energy levels and laser excitation scheme; (e) real time video[28].
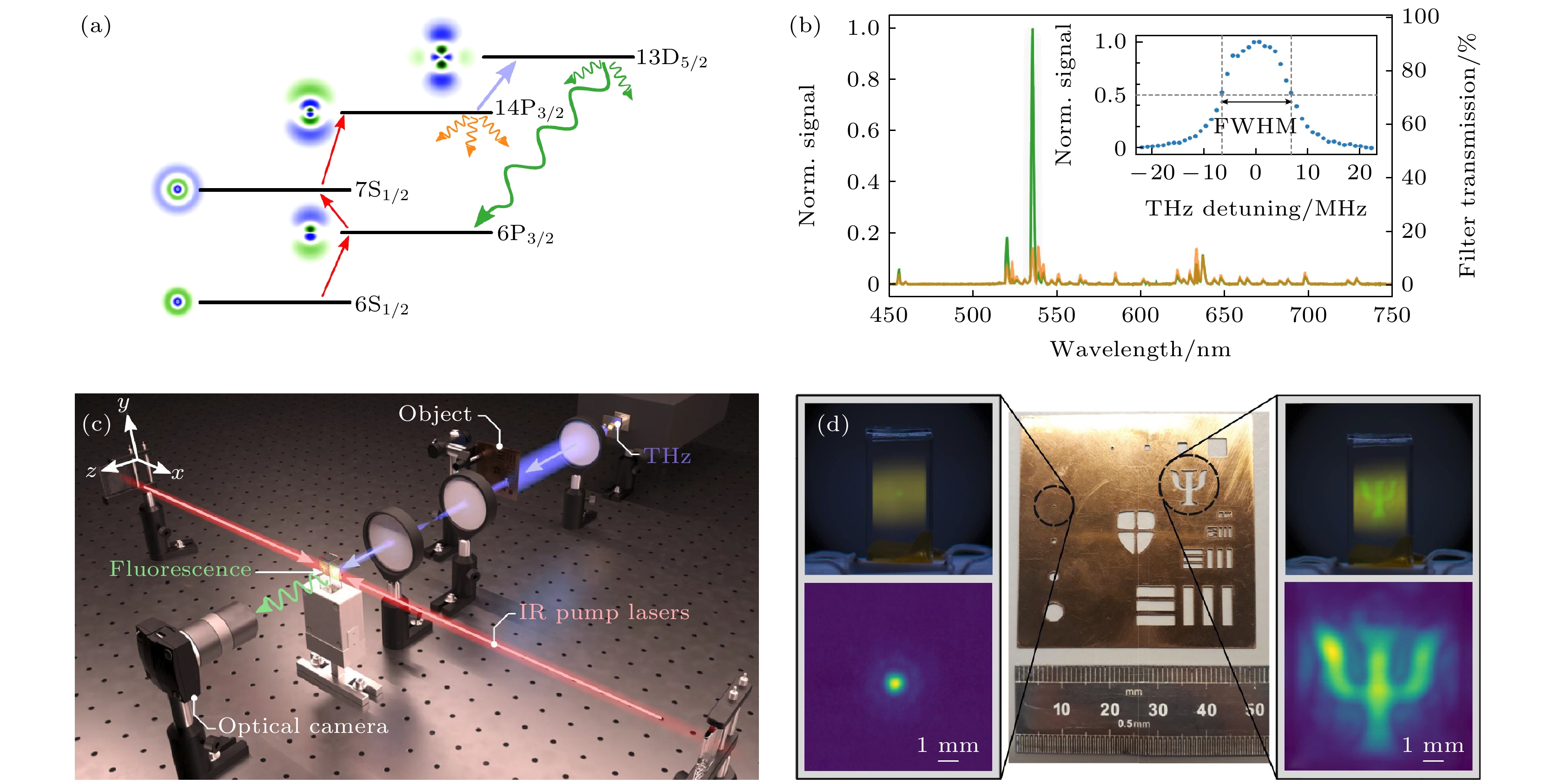
图 7 基于Rydberg原子太赫兹超高速成像 (a) 铯原子能级示意图; (b) THz场开启(绿色)和关闭(橙色)时的荧光光谱信号; (c) 实验装置图; (d) 放置在成像目标位置处的金属掩模[32]
Fig. 7. THz imaging at ultrahigh speed based on Rydberg atom: (a) Internal energy structure of caesium; (b) spectral characteristics of the fluorescence from the vapor, both with and without the THz field (green and orange lines, respectively); (c) diagram of the imaging setup described in this work; (d) metal mask (center) placed in the object plane of the system[32].
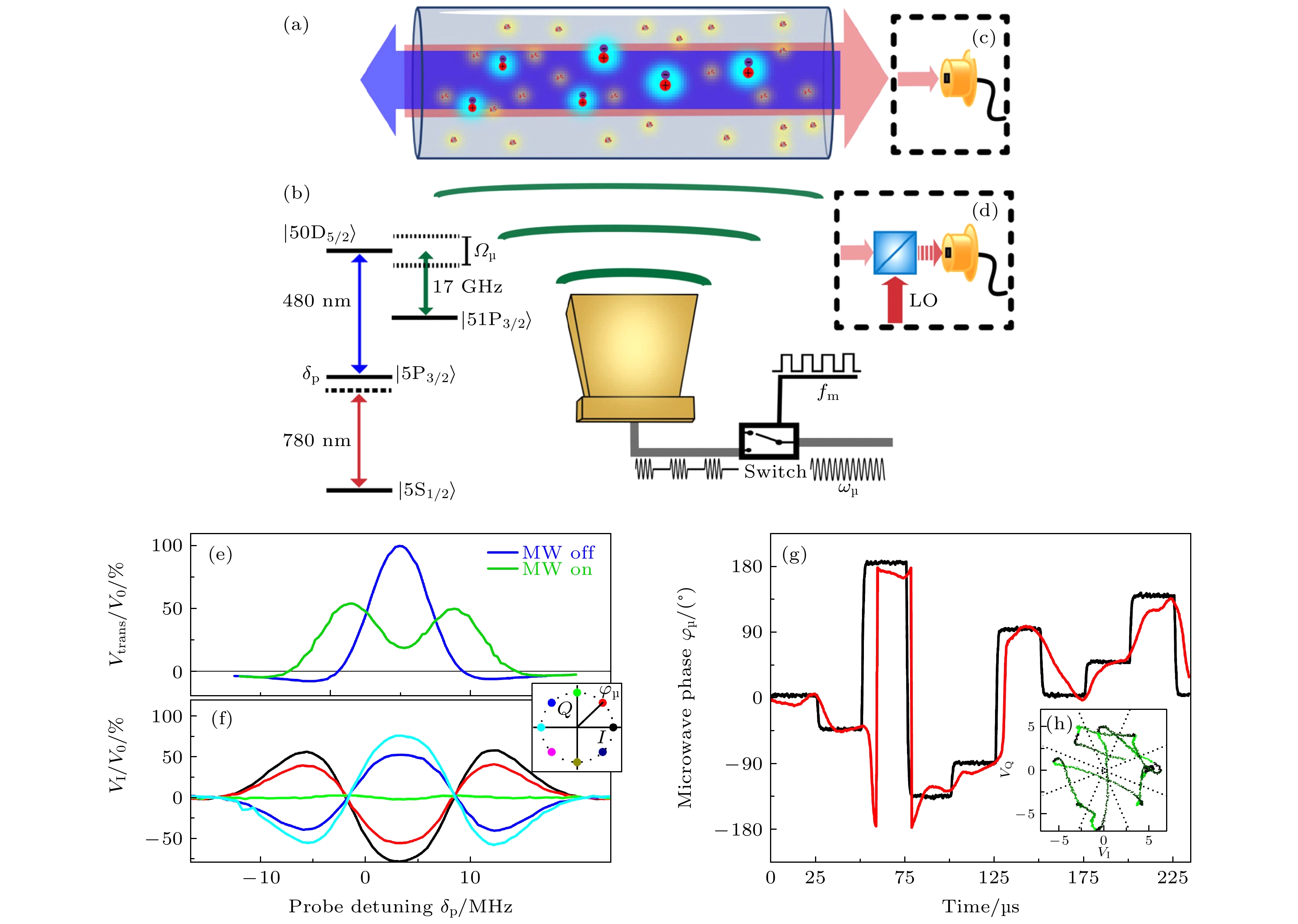
图 9 基于Rydberg原子天线的数字通信 (a) 实验装置图; (b) 能级示意图; (c) 使用光电探测器测量探测光; (d) 使用外差探头测量探测光; (e) Rydberg EIT (蓝色)和AT分裂(绿色); (f) 5种不同编码实例; (g) 接收到的8PSK相位信息; (h) 8PSK相位信息对应的相位轨迹[37]
Fig. 9. Digital communication based on Rydberg atom: (a) Experimental set-up used for the experiments; (b) energy level diagram for the a ladder-EIT system used for the experiments; (c) probe intensity modulation measured with a fast photodetector; (d) probe intensity modulation measured with an optical heterodyne; (e) Rydberg EIT (blue) and AT splitting (green) obtained by measuring probe transmission; (f) example demodulated transmission signals; (g) 8PSK sent and received phases; (h) phase constellation of the received phase in panel (g)[37].
图 10 (a) Rydberg四能级系统; (b) 当电磁场拉比频率为
$\varOmega_{\rm{T}} = 2 {\text {π}} \times[0,\; 1,\; 2.5,\; 5]$ MHz时, 分别对应的EIT-AT分裂模拟(黑色、红色、蓝色、绿色)Fig. 10. (a) Rydberg four-level system; (b) Autler-Townes splitting simulation for
$ \varOmega_{\rm{T}} = 2 {\text {π}} \times[0, \;1,\; 2.5,\; 5] $ MHz (black, red, blue and green solid line, respectively).
图 11 (a) Rydberg太赫兹实验装置示意图; (b) 实验中测到的不同太赫兹电场强度下的EIT信号(黑色实线, 太赫兹场关闭; 黄、粉、绿色实线, 增大信号源功率分别对应的AT分裂
$ \Delta $ f = 6.29, 12.44, 34.57 MHz)Fig. 11. (a) Schematic diagram of Rydberg terahertz experimental device; (b) transmission signal of probe laser (black solid line, without THz; yellow, pink and green solid line, with THz for
$ \Delta $ f = 6.29, 12.44, 34.57 MHz)表 1 铷和铯的Rydberg原子在THz频段的径向电偶极矩
Table 1. Radial part of electric dipole element between Rydberg states in the THz band for Rubidium and caesium.
铷原子 铯原子 径向电偶
极矩/$a_{0} e$对应跃迁
频率/THz径向电偶
极矩/$a_{0} e$对应跃迁
频率/THz509.687 0.342 513.125 0.339 424.780 0.449 421.685 0.456 376.294 0.542 379.324 0.535 336.314 0.642 339.203 0.634 302.964 0.750 301.320 0.759 266.916 0.909 275.101 0.861 263.079 0.933 265.677 0.919 233.146 1.116 232.273 1.127 229.824 1.145 208.101 1.315 201.655 1.392 201.108 1.404 
下载: 导出CSV
-
[1] Gallagher T F 1994 Rydberg Atoms (Cambridge: Cambridge University Press) pp38−49
[2] Sedlacek J A, Schwettmann A, Kübler H, Low R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
Google Scholar
[3] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
Google Scholar
[4] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003
Google Scholar
[5] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
Google Scholar
[6] Fan H Q, Kumar S, Daschner R, Kübler H, Shaffer J P 2014 Opt. Lett. 39 3030
Google Scholar
[7] Holloway C L, Gordon J A, Jeerts S, Schwarzkopf A, Anderson D A, Miller S A, Thaicharoen N, Raithel G 2014 IEEE Trans. Antenn. Propag. 62 6169
Google Scholar
[8] Gordon J A, Holloway C L, Schwarzkopf A, Anderson D A, Miller S, Thaicharoen N, Raithel G 2014 Appl. Phys. Lett. 105 024104
Google Scholar
[9] Holloway C L, Gordon J A, Schwarzkopf A, Anderson D A, Miller S A, Thaicharoen N, Raithel G 2014 Appl. Phys. Lett. 104 244102
Google Scholar
[10] Fan H Q, Kumar S, Sheng J T, Shaffer J P 2015 Phys. Rev. Appl. 4 044015
Google Scholar
[11] Fan H Q, Kumar S, Kübler H, Shaffer J P 2016 J. Phys. B 49 104004
Google Scholar
[12] Kumar S, Fan H Q, Kübler H, Jahangiri A J, Shaffer J P 2017 Opt. Express 25 8625
Google Scholar
[13] Kumar S, Fan H Q, Kübler H, Sheng J T, Shaffer J P 2017 Sci. Rep. 7 42981
Google Scholar
[14] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030
Google Scholar
[15] Song Z F, Liu H P, Liu X C, Zhang W F, Zou H Y, Zhang J, Qu J F 2019 Opt. Express 27 8848
Google Scholar
[16] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[17] Liao K Y, Tu H T, Yang S Z, Chen C J, Liu X H, Liang J, Zhang X D, Yan H, Zhu S L 2020 Phys. Rev. A 101 053432
Google Scholar
[18] Hafez H A, Chai X, Ibrahim A, Mondal S, Férachou D, Ropagnol X, Ozaki T 2016 J. Opt. 18 093004
Google Scholar
[19] Holloway C L, Simons M T, Haddab A H, Gordon J A, Anderson D A, Raithel G, Voran S D 2020 IEEE Antennas Propag. Mag.
Google Scholar
[20] 黄巍, 梁振涛, 杜炎雄, 颜辉, 朱诗亮 2015 64 160702
Google Scholar
Huang W, Liang Z T, Du Y X, Yan H, Zhu S L 2015 Acta Phys. Sin. 64 160702
Google Scholar
[21] 焦月春, 赵建明, 贾锁堂 2018 67 073201
Google Scholar
Jiao Y C, Zhao J M, Jia S T 2018 Acta Phys. Sin. 67 073201
Google Scholar
[22] Wade C G 2018 Terahertz Wave Detection and Imaging with a Hot Rydberg Vapour (Switzerland: Springer Theses) pp55−63
[23] Hughes I, Hase T 2010 Measurements and Their Uncertainties (Oxford: Oxford University Press) pp74−83
[24] Šibalić N, Pritchard J D, Adams C S, Weatherill K J 2017 Comput. Phys. Commun. 220 319
Google Scholar
[25] Raimond J M, Goy P, Vitrant G, Haroche S 1981 J. Phys. Colloques 42 C8-37
Google Scholar
[26] Drabbels M, Noordam L D 1999 Appl. Phys. Lett. 74 1797
Google Scholar
[27] Gurtler A, Meijer A S, Van der Zande W J 2003 Appl. Phys. Lett. 83 222
Google Scholar
[28] Wade C G, Šibalić N, De Melo N R, Kondo J M, Adams C S, Weatherill K J 2016 Nat. Photonics 11 40
Google Scholar
[29] Mitrofanov O, Tan T, Mark P R, Bowden B, Harrington J A 2009 Appl. Phys. Lett. 94 171104
Google Scholar
[30] Bitzer A, Walther M 2008 Appl. Phys. Lett. 92 231101
Google Scholar
[31] Seo M A, Adam A J L, Kang J H, Lee J W, Jeoung S C, Park Q H, Planken P C M, Kim D S 2007 Opt. Express 15 11781
Google Scholar
[32] Downes L A, MacKellar A T, Whiting D J, Bourgenot C, Adams C S, Weatherill K J 2020 Phys. Rev. X 10 011027
Google Scholar
[33] Jansen C, Wietzke S, Peters O, Scheller M, Vieweg N, Salhi M, Krumbholz N, Jrdens C, Hochrein T, Koch M 2010 Appl. Opt. 49 E48
Google Scholar
[34] Jepsen P, Cooke D, Koch M 2011 Laser Photonics Rev. 5 124
Google Scholar
[35] Mittleman D M 2018 Opt. Express 26 9417
Google Scholar
[36] Hanzo L, Webb W T, keller T 2000 Single- and Multi-carrier Quadrature Amplitude Modulation: Principles and Applications for Personal Communications, WATM and Broadcasting (2nd Ed.) (Southampton: Wiley-IEEE Press) pp23−56
[37] Meyer D H, Cox K C, Fatemi F K, Kunz P D 2018 Appl. Phys. Lett. 112 211108
Google Scholar
下载:
计量
- 文章访问数: 10816
- PDF下载量: 655
- 被引次数: 0
