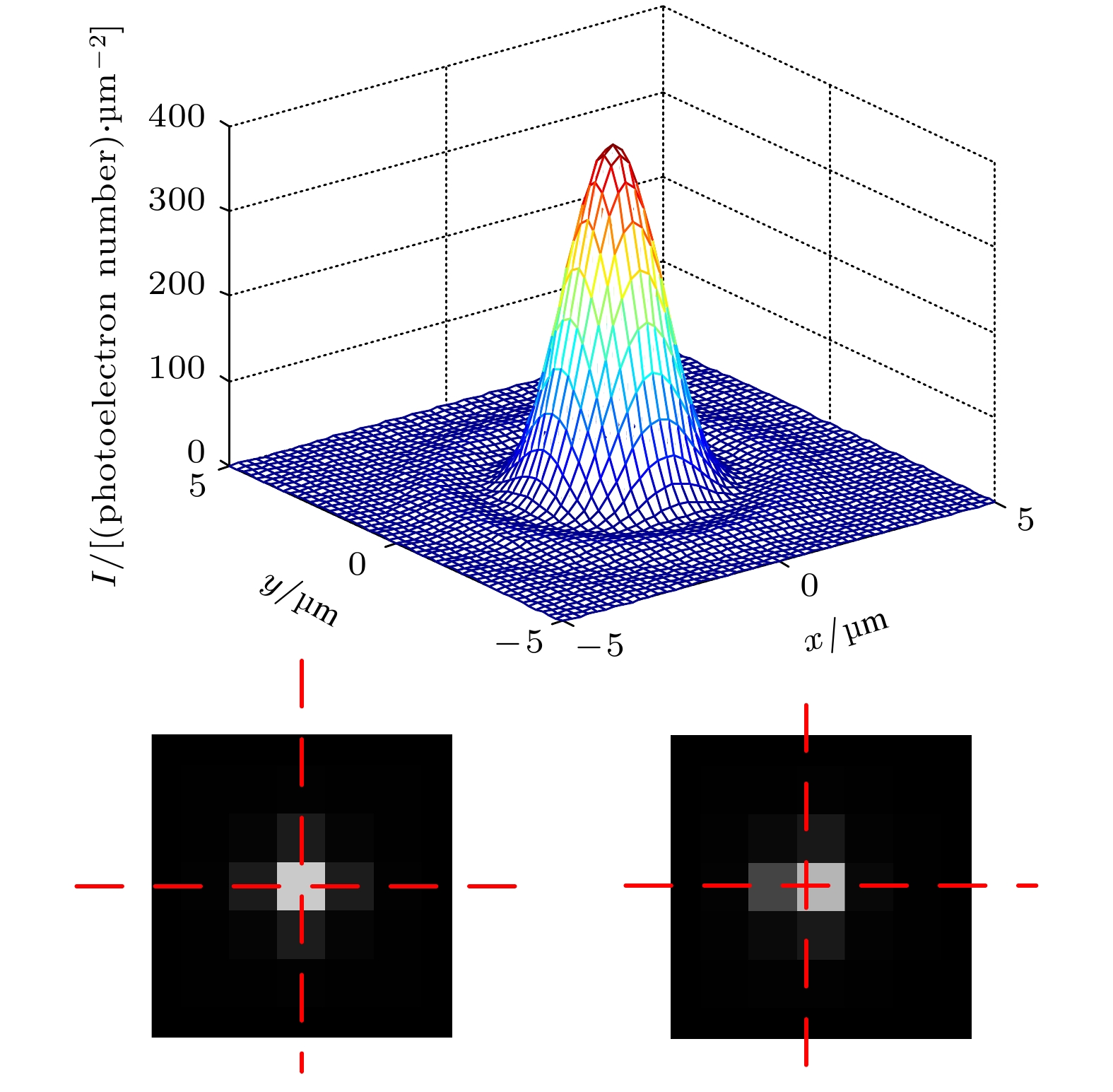
-
纳米级乃至更高精度的测量是原子及近原子尺度制造技术发展的基础和保障. 光学测量具有精度高、测量范围广、测量直观等优点, 其对单个成像光斑中心的定位可达远超衍射极限的精度. 但由于光本身散粒噪声、探测器暗电流噪声等随机性的存在, 光学测量存在精度极限. 本文基于克拉美罗下界理论发展了可适用于任意强度分布像斑的精度极限计算方法, 并以典型艾里斑为例, 分析了成像过程中反映信噪比、能量集中度、计算方式的参数对定位精度极限的影响规律并给出提高精度的建议和结论. 对实验所得像斑进行了精度极限计算, 验证了所得结论对类似艾里斑的像斑的适用性. 研究为原子及近原子尺度制造过程中光学测量的应用和优化提供了分析方法和理论指导.Measurement technology with nanometer scale or higher level precision is the basis and guarantee for developing atomic and close-to-atomic scale manufacturing. Optical measurement has the advantages of high precision, wide range and real-time measurement. The precision of localizing a single imaging spot’s center is not limited by the diffraction limit and could reach nanometer scale. However, the shot noise of light and the dark current noise of the detector bring about a precision limit for optical measurement. Based on the Cramer-Rao lower bound theory, a precision limit estimation method for general imaging profiles is developed in this paper. Taking the typical Airy spot for example, the influences of the parameters such as signal-to-noise ratio, energy concentration and processing method on the positioning precision limit are analyzed, and suggestions and conclusions for improving the measurement precision are given. The precision limit of a laboratory imaging spot is calculated, which verifies that the conclusions are also suitable for the imaging profiles similar to the Airy spot. The research provides the analytical method and theoretical guidance for the application and optimization of optical measurement in atomic and close-to-atomic scale manufacturing.
[1] Fang F Z, Zhang N, Guo D M, Kornel E, Benny C, Liu K, Kazuya Y 2019 Int. J. Extrem. Manuf. 1 012001
Google Scholar
[2] 房丰洲 2020 中国机械工程 537 5
Fang F Z 2020 China Mech. Eng. 537 5
[3] Betzig E, Patterson G H, Sougrat R, Lindwasser O W, Olenych S, Bonifacino J S, Davidson M W, Lippincott-Schwartz J, Hess H F 2006 Science 313 1642
Google Scholar
[4] Manley S, Gillette J M, Patterson G H, Shroff H, Hess H F, Betzig E, Lippincott-Schwartz J 2008 Nat. Methods 5 155
Google Scholar
[5] Patterson G, Davidson M, Manley S, Lippincott-Schwartz J 2010 Annu. Rev. Phys. Chem. 61 345
Google Scholar
[6] Bates M, Huang B, Dempsey G T, Zhuang X 2007 Science 317 1749
Google Scholar
[7] Schmidt R, Wurm C A, Punge A, Egner A, Jakobs S, Hell S W 2009 Nano Lett. 9 2508
Google Scholar
[8] Folling J, Bossi M, Bock H, Medda R, Wurm C A, Hein B, Jakobs S, Eggeling C, Hell S W 2008 Nat. Methods 5 943
Google Scholar
[9] Hess S T, Gould T J, Gudheti M V, Maas S A, Mills K D, Zimmerberg J 2007 Proc. Natl. Acad. Sci. 104 17370
Google Scholar
[10] Shroff H, Galbraith C G, Galbraith J A, Betzig E 2008 Nat. Methods 5 417
Google Scholar
[11] Yildiz A, Forkey J N, McKinney S A, Ha T, Goldman Y E, Selvin P R 2003 Science 300 2061
Google Scholar
[12] Hidaka Y, Ishikawa M 2012 US Patent 8 223 345
[13] Shaklan S, Sharman M C, Pravdo S H 1995 Appl. Opt. 34 6672
Google Scholar
[14] Shao M, Nemati B, Zhai R, Goullioud R, Malbet F, Leger A 2011 Proc. SPIE. 8151 81510V
Google Scholar
[15] Malbet F, Crouzier A, Leger A, Shao M, Goullioud R, Lagage P, Delpech M 2013 Proc. SPIE 8864 88641D
Google Scholar
[16] Joonhyung K, Jeawan H, Yong-Seok K, Dong-Youn L, Kyumin L, Sang-min L, Sang-il P 2003 Rev. Sci. Instrum. 74 4378
Google Scholar
[17] Wang Y L, Wang H M, Bi S S 2014 AIP Adv. 4 057130
Google Scholar
[18] EMVA https://www.emva.org/wp-content/uploads/EMVA1288-3.1 a.pdf [2020-11-15]
[19] Winick K A, 1986 J. Opt. Soc. Am. A 3 1809
Google Scholar
[20] Wang Y L, Li X L, Bi S S, Zhu X F, Liu J H 2017 Meas. Sci. Technol. 28 015402
Google Scholar
[21] Fisher R A 1922 Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 222 309
[22] Rao C R 1992 Breakthroughs in Statistics (New York: Springer) p235
[23] Rao C R 1947 Math. Proc. Camb. Philos. Soc. 43 280
Google Scholar
[24] Janesick J, Klaasen K, Elliott T 1985 Proc. SPIE 570 7
Google Scholar
-
图 1 艾里斑的光强分布函数及相应的像素灰度响应示例
Fig. 1. Intensity function of an Airy spot and its corresponding pixel response.
图 2 精度极限-像素相位曲面 (a) 中心强度为400, 暗电流噪声为0; (b) 中心强度为400, 暗电流噪声为25
Fig. 2. Relationship of the precision limit to the x and y pixel phase: (a) The central intensity is 400, the dark current noise is 0; (b) the central intensity is 400, the dark current noise is 25.
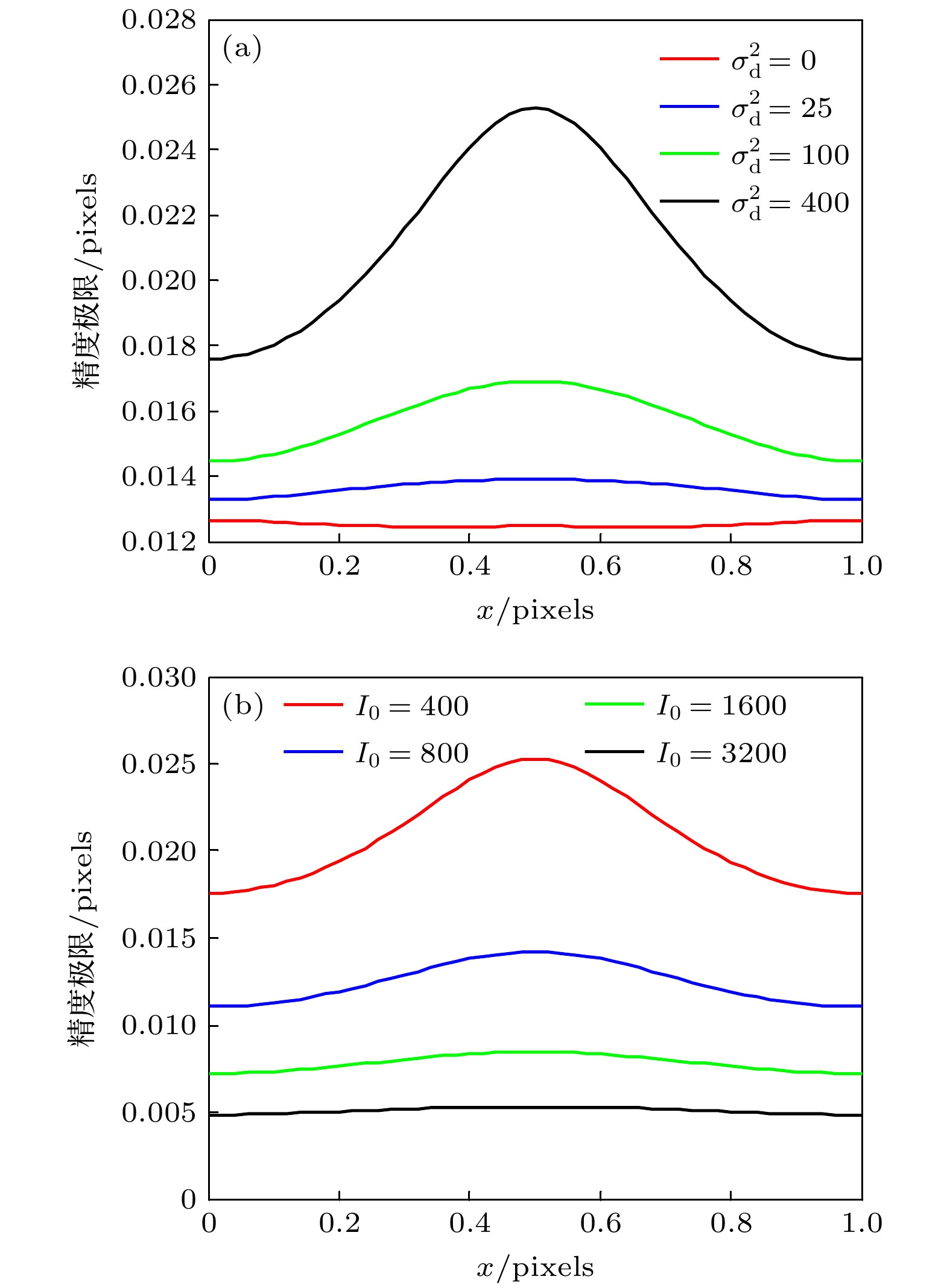
图 3 y像素相位为0.5时的精度极限-x像素相位曲线 (a) 中心强度为400, 暗电流噪声分别取0, 25, 100, 400; (b) 暗电流噪声为400, 中心强度分别取400, 800, 1600, 3200
Fig. 3. Relationship of the precision limit and the x pixel phase when the y pixel phase is 0.5: (a) The central intensity is 400, the dark current noise is 0, 25, 100, 400, respectively; (b) the dark current noise is 400, the central intensity is 400, 800, 1600, 3200, respectively.
图 4 精度极限-像素相位曲面 (a) F数为2; (b) F数为8
Fig. 4. Relationship of the precision limit to the x and y pixel phase: (a) The F of the optical system is 2; (b) the F of the optical system is 8.
图 5 y像素相位为0.5时的精度极限-x像素相位曲线
Fig. 5. Relationship of the precision limit and the x pixel phase when the y pixel phase is 0.5.
图 6 精度极限-像素相位曲面 (a) 计算窗口为3 × 3; (b) 计算窗口为5 × 5
Fig. 6. Relationship of the precision limit to the x and y pixel phase: (a) The size of the window used for localization is 3 × 3; (b) the size of the window is 5 × 5.
图 8 实验室像斑的精度极限-x像素相位曲线 (a) 能量较集中强度分布; (b) 能量较发散强度分布
Fig. 8. Relationship of the precision limit and the x pixel phase for laboratory obtained image spots: (a) The precision limit for a energy concentrated spot; (b) the precision limit for a spot with lower energy concentration.
表 1 不同能量和噪声条件下σall和Δstd结果(保留小数点后四位)
Table 1. Results of σall and Δstd under different levels of spot energy and noise.
σall (Δstd)/pixels $\sigma _{\rm{d}}^{\rm{2}}$ = 0 $\sigma _{\rm{d}}^{\rm{2}}$ = 25 $\sigma _{\rm{d}}^{\rm{2}}$ = 100 $\sigma _{\rm{d}}^{\rm{2}}$ = 400 ${I_{\rm{0}}} = {\rm{400}}$ 0.0125 (0.0001) 0.0136 (0.0003) 0.0157 (0.0011) 0.0217 (0.0033) ${I_{\rm{0}}} = {\rm{800}}$ 0.0088 (0.0001) 0.0093 (0.0001) 0.0102 (0.0004) 0.0127 (0.0014) ${I_{\rm{0}}} = {\rm{1600}}$ 0.0062 (0.0001) 0.0064 (0.0000) 0.0068 (0.0001) 0.0079 (0.0006) ${I_{\rm{0}}} = {\rm{3200}}$ 0.0044 (0.0000) 0.0045 (0.0000) 0.0046 (0.0000) 0.0051 (0.0002) 
下载: 导出CSV
表 2 不同能量集中度条件下精度极限结果
Table 2. Results of the precision limit under different levels of spot energy concentration
RF = 0.25 RF = 0.50 RF = 1.00 RF = 2.00 σall/pixels 0.0335 0.0192 0.0136 0.0247 Δstd/pixels 0.0211 0.0122 0.0003 0.0002 最优精度/pixels 0.0033 (边缘) 0.0065 (边缘) 0.0130 (边缘) 0.0244 (边缘) 最差精度/pixels 0.0803 (中心) 0.0566 (中心) 0.0139 (中心) 0.0250 (中心) 衍射极限/pixels 0.3050 0.6100 1.2200 2.4400
下载: 导出CSV
-
[1] Fang F Z, Zhang N, Guo D M, Kornel E, Benny C, Liu K, Kazuya Y 2019 Int. J. Extrem. Manuf. 1 012001
Google Scholar
[2] 房丰洲 2020 中国机械工程 537 5
Fang F Z 2020 China Mech. Eng. 537 5
[3] Betzig E, Patterson G H, Sougrat R, Lindwasser O W, Olenych S, Bonifacino J S, Davidson M W, Lippincott-Schwartz J, Hess H F 2006 Science 313 1642
Google Scholar
[4] Manley S, Gillette J M, Patterson G H, Shroff H, Hess H F, Betzig E, Lippincott-Schwartz J 2008 Nat. Methods 5 155
Google Scholar
[5] Patterson G, Davidson M, Manley S, Lippincott-Schwartz J 2010 Annu. Rev. Phys. Chem. 61 345
Google Scholar
[6] Bates M, Huang B, Dempsey G T, Zhuang X 2007 Science 317 1749
Google Scholar
[7] Schmidt R, Wurm C A, Punge A, Egner A, Jakobs S, Hell S W 2009 Nano Lett. 9 2508
Google Scholar
[8] Folling J, Bossi M, Bock H, Medda R, Wurm C A, Hein B, Jakobs S, Eggeling C, Hell S W 2008 Nat. Methods 5 943
Google Scholar
[9] Hess S T, Gould T J, Gudheti M V, Maas S A, Mills K D, Zimmerberg J 2007 Proc. Natl. Acad. Sci. 104 17370
Google Scholar
[10] Shroff H, Galbraith C G, Galbraith J A, Betzig E 2008 Nat. Methods 5 417
Google Scholar
[11] Yildiz A, Forkey J N, McKinney S A, Ha T, Goldman Y E, Selvin P R 2003 Science 300 2061
Google Scholar
[12] Hidaka Y, Ishikawa M 2012 US Patent 8 223 345
[13] Shaklan S, Sharman M C, Pravdo S H 1995 Appl. Opt. 34 6672
Google Scholar
[14] Shao M, Nemati B, Zhai R, Goullioud R, Malbet F, Leger A 2011 Proc. SPIE. 8151 81510V
Google Scholar
[15] Malbet F, Crouzier A, Leger A, Shao M, Goullioud R, Lagage P, Delpech M 2013 Proc. SPIE 8864 88641D
Google Scholar
[16] Joonhyung K, Jeawan H, Yong-Seok K, Dong-Youn L, Kyumin L, Sang-min L, Sang-il P 2003 Rev. Sci. Instrum. 74 4378
Google Scholar
[17] Wang Y L, Wang H M, Bi S S 2014 AIP Adv. 4 057130
Google Scholar
[18] EMVA https://www.emva.org/wp-content/uploads/EMVA1288-3.1 a.pdf [2020-11-15]
[19] Winick K A, 1986 J. Opt. Soc. Am. A 3 1809
Google Scholar
[20] Wang Y L, Li X L, Bi S S, Zhu X F, Liu J H 2017 Meas. Sci. Technol. 28 015402
Google Scholar
[21] Fisher R A 1922 Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 222 309
[22] Rao C R 1992 Breakthroughs in Statistics (New York: Springer) p235
[23] Rao C R 1947 Math. Proc. Camb. Philos. Soc. 43 280
Google Scholar
[24] Janesick J, Klaasen K, Elliott T 1985 Proc. SPIE 570 7
Google Scholar
下载:
计量
- 文章访问数: 7122
- PDF下载量: 299
- 被引次数: 0
