-
利用Rydberg原子作为微波传感器实现了微弱场的测量与通信. 在铯原子蒸气池中, 相向传输的探测光(852 nm)和耦合光(510 nm)与铯原子相互作用形成阶梯型三能级电磁感应透明光谱, 用于实现Rydberg原子的光学探测. 频率约为 2.19 GHz的强微波场作为本地场
$ (E_{{\rm{L}}}) $ , 共振耦合相邻的两个Rydberg能级$|68{\rm{D}}_{5/2}\rangle$ 和$|69{\rm{P}}_{3/2}\rangle$ , 与具有一定失谐$ {\text {δ}} f $ 的待测微弱信号场$(E_{{\rm{S}}})$ 同时作用于Rydberg原子. Rydberg原子作为微波混频器可直接读出两束微波的差频信号, 实现待测信号场的高灵敏探测, 对应的最小测量值为$E_{0} = 1.7\;$ μV/cm, 频率分辨率小于1 Hz. 在此基础上, 对微弱信号场进行编码, 实验上很好地还原了加载到微波弱场上的基带信号, 测量的传输带宽达200 MHz, 实现了微弱场条件下的通信.We present a high-sensitivity weak microwave measurement and communication technology by employing the Rydberg beat technique. The Rydberg cascade three-level system is composed of a cesium ground state$6{\rm{S}}_{1/2}$ , an excited state$6{\rm{P}}_{3/2}$ , and a Rydberg state$n{\rm{D}}_{5/2}$ in a room-temperature cesium cell. A two-photon resonant Rydberg electromagnetic induced transparency (EIT) is used to optically detect the Rydberg level, in which a weak probe laser is locked at the resonant transition of$|6{\rm{S}}_{1/2}\rangle \rightarrow |6{\rm{P}}_{3/2}\rangle$ , and a strong coupling laser drives the transition of$|6{\rm{P}}_{3/2}\rangle \rightarrow |n{\rm{D}}_{5/2}\rangle$ . Both lasers are locked with a high-precision Fabry-Perot cavity. Two E-fields are incident into the vapor cell to interact with Rydberg atoms via a microwave horn, one is a strong microwave field with frequency 2.19 GHz, acting as a local field ($E_{{\rm{L}}}$ ) and resonantly coupling with two Rydberg energy levels,$|68{\rm{D}}_{5/2}\rangle$ and$|69{\rm{P}}_{3/2}\rangle$ , and the other is a weak signal field ($E_{{\rm{S}}}$ ) with frequency difference${\text{δ}} f$ , interacting with the same Rydberg levels. The wave-absorbing material is placed around the vapor cell to reduce the reflection of microwave field. In the presence of the local field, the Rydberg atoms are employed as a microwave mixer for reading out the difference frequency${\text{δ}}f$ oscillation signal, which is proportional to the amplitude of weak signal field. The minimum detectable field of$E_{0} = 1.7$ μV/cm is obtained when the lock-in output reaches the base noise. We also measure the frequency resolution of the Rydberg mixer by changing the${\text{δ}} f$ with fixed$ f_{\rm ref} $ , thus achieving a frequency resolution better than 1 Hz. For neighboring fields with 1 Hz away from the signal field, an isolation of 60 dB is achieved. Furthermore, we use the Rydberg atom as an antenna to receive the baseband signals encoded into the weak microwave field, demonstrating that the receiver has a transmission bandwidth of about 200 MHz. The demonstration of sensitivity of Rydberg atoms to microwave field is particularly useful in many areas, such as quantum precise measurement and quantum communications. In general, this technique can be extended to the detection of electromagnetic radiation from the radio-frequency regime to the tera-hertz range and is feasible for fabricating a miniaturized devices, thereby providing us with a way to receive the information encoded in tera-hertz carriers in future work.-
Keywords:
- Rydberg atom /
- weak electromagnetic field measurement /
- communication
[1] Levanon N 1988 Radar Principles (New York: John Wiley & Sons) pp120−145
[2] Doviak R J, Zrnic D S 1993 Doppler Radar And Weather Observations (2nd Ed.) (New York: Academic Press) pp64−85
[3] Carr J J 1996 Microwave and Wireless Communications Technology (Newton: Butterworth-Heinemann) pp406−427
[4] Kanda M, Driver L D 1987 IEEE Trans. Antennas Propag. 35 33
Google Scholar
[5] Kanda M, Driver L D 1987 IEEE Trans. Microwave Theory Tech. 35 124
[6] Kanda M 1993 IEEE Trans. Antennas Propag. 41 1349
Google Scholar
[7] Stock M 2018 Meas. Tech. 60 1169
Google Scholar
[8] Gallagher T F 1994 Rydberg Atom (Cambridge: Cambridge University Press) pp11–47
[9] Jiao Y C, Hao L P, Han X X, Bai S Y, Raithel G, Zhao J M, Jia S T 2017 Phys. Rev. Appl. 8 014028
Google Scholar
[10] Harris S E 1997 Phys. Today 50 36
[11] Xiao M, Li Y Q, Jin S Z, Banacloche J G 1995 Phys. Rev. Lett. 74 666
Google Scholar
[12] Banacloche J G, Li Y Q, Jin S Z, Xiao M 1995 Phys. Rev. A 51 576
Google Scholar
[13] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003
Google Scholar
[14] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
Google Scholar
[15] Mohapatra A K, Bason M G, Butscher B, Weatherill K J, Adams C S 2008 Nat. Phys. 4 890
Google Scholar
[16] Autler S H, Townes C H 1955 Phys. Rev. 100 703
Google Scholar
[17] Cahuzac Ph, Vetter R 1976 Phys. Rev. A 14 270
Google Scholar
[18] Picqué J L, Pinard J 1976 J. Phys. B 9 L77
Google Scholar
[19] Kumar S, Fan H Q, Kübler H, Sheng J T, Shaffer J P 2017 Sci. Rep. 7 42981
Google Scholar
[20] Huang W, Liang Z T, Du Y X, Yan H, Zhu S L 2015 Acta Phys. Sin. 64 160702
Google Scholar
[21] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
Google Scholar
[22] Osterwalder A, Merkt F 1999 Phys. Rev. Lett. 82 1831
Google Scholar
[23] Downes L A, MacKellar A R, Whiting D J, Bourgenot C, Adams C S, Weatherill K J 2020 Phys. Rev. X 10 011027
Google Scholar
[24] Liao K Y, Tu H T, Yang S Z, Chen C J, Liu X H, Liang J, Zhang X D, Yan H, Zhu S L 2020 Phys. Rev. A 101 053432
Google Scholar
[25] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[26] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030
Google Scholar
[27] Hao L P, Xue Y M, Fan J B, Bai J X, Jiao Y C, Zhao J M 2020 Chin. Phys. B 29 033201
Google Scholar
[28] Deb A B, Kjærgaard N 2018 Appl. Phys. Lett. 112 211106
Google Scholar
[29] Meyer D H, Cox K C, Fatemi F K, Kunz P D 2018 Appl. Phys. Lett. 112 211108
Google Scholar
[30] Jiao Y C, Han X X, Fan J B, Georg R, Zhao J M, Jia S T 2019 Appl. Phys. Express 12 126002
Google Scholar
[31] Song Z F, Liu H P, Liu X C, Zhang W F, Zou H Y, Zhang J, Qu J F 2019 Opt. Express 27 8848
Google Scholar
[32] Anderson D A, Sapiro R E, Raithel G 2020 IEEE Trans. Antennas Propag. 10 1109
Google Scholar
[33] Holloway C L, Simons M T, Gordon J A, Novotny D 2019 IEEE Antennas Wirel. Propag. Lett. 18 1853
Google Scholar
[34] 樊佳蓓, 焦月春, 郝丽萍, 薛咏梅, 赵建明, 贾锁堂 2018 67 093201
Google Scholar
Fan J B, Jiao Y C, Hao L P, Xue Y M, Zhao J M, Jia S T 2018 Acta Phys. Sin. 67 093201
Google Scholar
[35] Bai J X, Fan J B, Hao L P, Spong N L R, Jiao Y C, Zhao J M 2019 Appl. Sci. 9 4895
Google Scholar
-
图 1 (a) 实验装置图.
$\lambda_{{\rm{p}}}$ = 852 nm的探测光与$\lambda_{{\rm{c}}}$ = 510 nm的耦合光相向作用于铯原子蒸气池中, 两束激光偏振相同. 探测光经偏振分光棱镜(PBS)分为两束, 一束与耦合光重合形成EIT, 另一束作为背景光通过蒸气池, 两束光经样品池后进入平衡零拍探测器(PDB), 以减小由于功率起伏引起的噪声. 较强的本地场$(E_{{\rm{L}}})$ 与待测信号场$(E_{{\rm{S}}})$ 合束后通过微波喇叭出射作用于铯原子. 吸波材料(WAM)置于蒸气池周围以减少由光学元件引起微波反射而产生的测量误差. 当此装置用于通信信号的传输时, 将基带信号由幅度调制方式加载到弱信号场. (b) 四能级原子示意图. 探测光$\lambda_{\rm p}$ 共振作用于铯原子基态$|6 {\rm{S}}_{1/2}\rangle$ 至激发态$|6 {\rm{P}}_{3/2}\rangle$ 的跃迁. 耦合光$\lambda_{\rm{c}}$ 作用于$|6 {\rm{P}}_{3/2}\rangle \rightarrow |68 {\rm{D}}_{5/2}\rangle$ 的Rydberg跃迁. 本地场$(E_{{\rm{L}}})$ 共振耦合相邻的Rydberg能级$|68 {\rm{D}}_{5/2}\rangle$ 与$|69 {\rm{P}}_{3/2}\rangle$ , 待测弱场$(E_{{\rm{S}}})$ 与本地场相差频率${\text{δ}} f$ Fig. 1. (a) Sketch of the experimental setup. A probe laser,
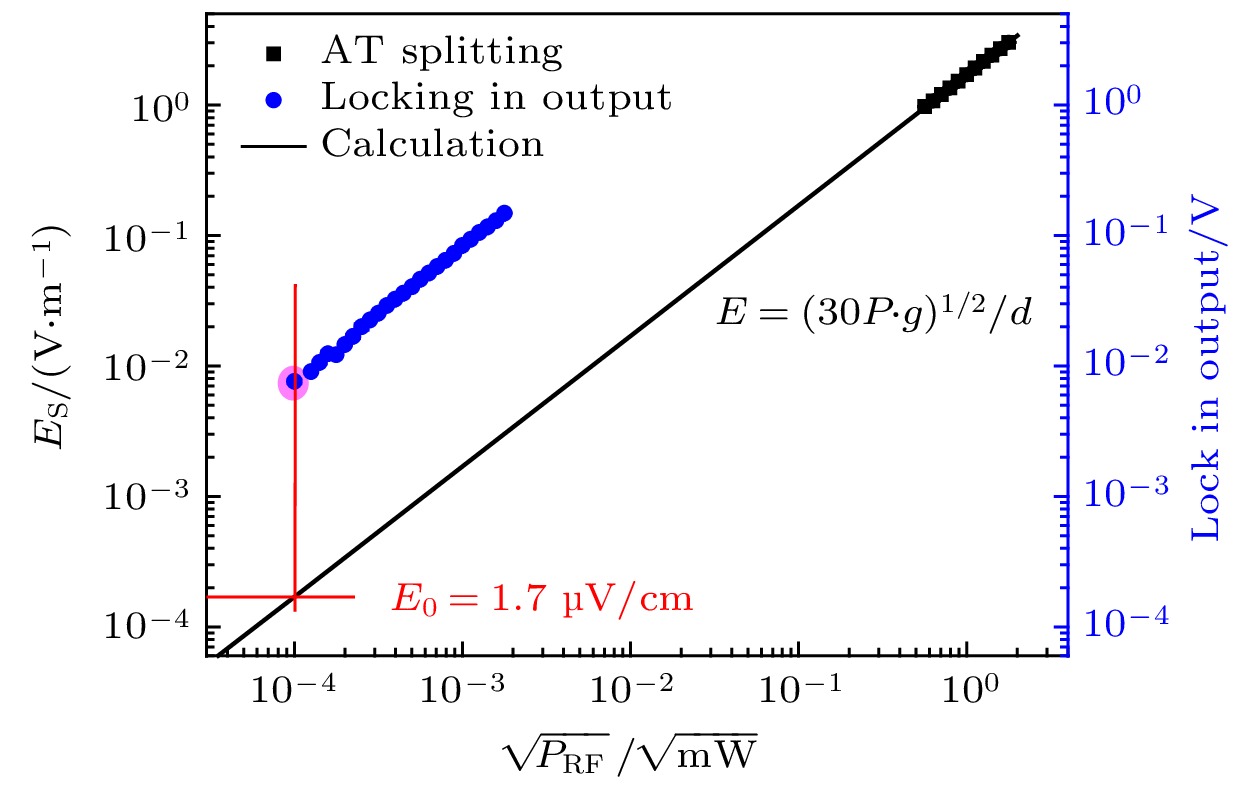
$\lambda_{{\rm{p}}}$ = 852 nm, and a coupling laser,$\lambda_{{\rm{c}}}$ = 510 nm, are counter-propagated through a cesium room-temperature cell with same polarization. An 852 nm laser is separated into two with a PBS, one is counter-propagated with the coupling laser forming EIT, while the other passes through the vapor cell as a reference beam. Both are detected with a PDB to reduce the background noise caused by laser power fluctuation. A strong local field$(E_{{\rm{L}}})$ and the weak signal field$(E_{{\rm{S}}})$ are combined by a power combiner and coupled to free space to interact with Rydberg atoms via a microwave horn. The WAM is placed around the vapor cell to reduce reflection of microwave field. The baseband signal is encoded into the weak signal field with amplitude modulation when communication signals are transferred. PBS, polarizing beam splitter; PDB, balanced amplified photo-detectors; WAM, wave-absorbing material. (b) Diagram of four-level scheme. A probe laser is resonant with the ground transition,$|6 {\rm{S}}_{1/2}\rangle$ $\rightarrow$ $|6 {\rm{P}}_{3/2}\rangle$ , and the coupling laser drives the Rydberg transition,$|6 {\rm{P}}_{3/2}\rangle \rightarrow |68 {\rm{D}}_{5/2}\rangle$ . The local field$(E_{{\rm{L}}})$ is resonant with two Rydberg levels$|68 {\rm{D}}_{5/2}\rangle$ and$|69 {\rm{P}}_{3/2}\rangle$ , the weak signal field$(E_{{\rm{S}}})$ has frequency difference${\text{δ}} f$ with local field
图 2 测量的微波场强与信号源输出功率的依赖关系, 黑色方点表示EIT-AT分裂测量的结果, 蓝色圆点表示拍频测量的结果. 黑色实线表示由(5)式计算的电场值与微波输出功率的关系, 与实验测量相符. 最小测量电场为
$E_{0}=1.7$ μV/cm, 如图中红色阴影圈所示Fig. 2. Microwave field measurements as a function of square root of the output power. The black squares show EIT-AT measurements and blue circles for beat method. The black solid line shows the calculation of Eq. (5). The measurable minimum field is
$E_{0}=1.7$ μV/cm, as shown with the red shadow circle
图 3 拍频的隔离特性和频率分辨率测量. 设置时间常数为1 s, 分别
$f_{{\rm{ref}}}$ 与${\text{δ}} f$ 的频率差为 0.1, 0.5, 1, 10 Hz时, 测量锁相放大器的输出电平信号. 1 Hz的频差对应60 dB的隔离, 0.5 Hz的频差可以实现40 dB信号的隔离. 拍频微波测量技术可实现亚赫兹的频率分辨, 最小的频率分辨率达0.1 Hz. 灰色阴影部分表示基底噪声信号, 约为–15 dBFig. 3. Measurements of the isolation and frequency resolution. The lock-in output levels are obtained with the time constant 1 s and the difference of
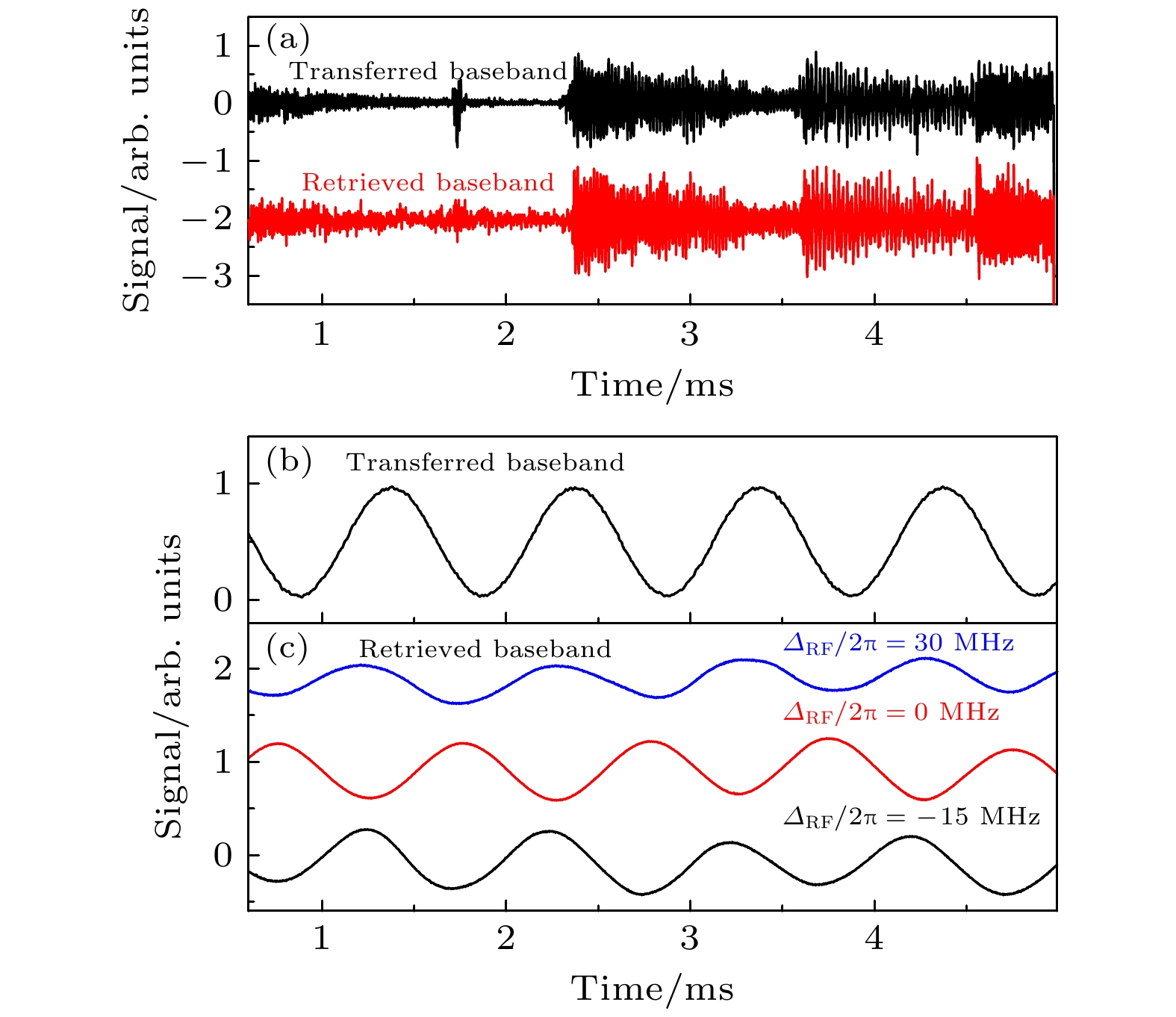
$f_{{\rm{ref}}}$ and${\text{δ}} f$ are 0.1, 0.5, 1, and 10 Hz, respectively. The frequency difference of 1 Hz (0.5 Hz) corresponds to the isolation of 60 dB (40 dB). The beat frequency microwave measurement can realize the frequency resolution of sub-Hz, with the minimum frequency resolution up to 0.1 Hz. The grey area around –15 dB is base noise
图 4 (a)基于Rydberg原子拍频技术实现的音频信号的传输与提取. 将音频信号加载到弱信号场(160 µV/cm)上, Rydberg原子实现了信号的直接提取. 黑色实线表示传输的音频信号, 红色线表示Rydberg原子直接读取的音频信号. (b) 传输的调制频率为1 kHz的基带信号. (c) 在信号场为50 μV/cm时, 微波场失谐
$\varDelta_{{\rm{RF}}}/2{\text{π}}$ 分别为30, 0, –15 MHz 时的Rydberg 原子读出的信号Fig. 4. (a) Demonstration of transfer and readout of the baseband signal based on Rydberg beat method. The audio signal is amplitude modulated into the weak carrier field of 160 μV/cm, Rydberg atoms are used to readout the transferred audio signal. The top line represents the original transferred signal, and the bottom line displays the retrieved signal. (b) A 1 kHz baseband signal is encoded into the weak carrier field (50 μV/cm) with the amplitude modulation method. (c) The retrieved baseband signals based on Rydberg atoms for
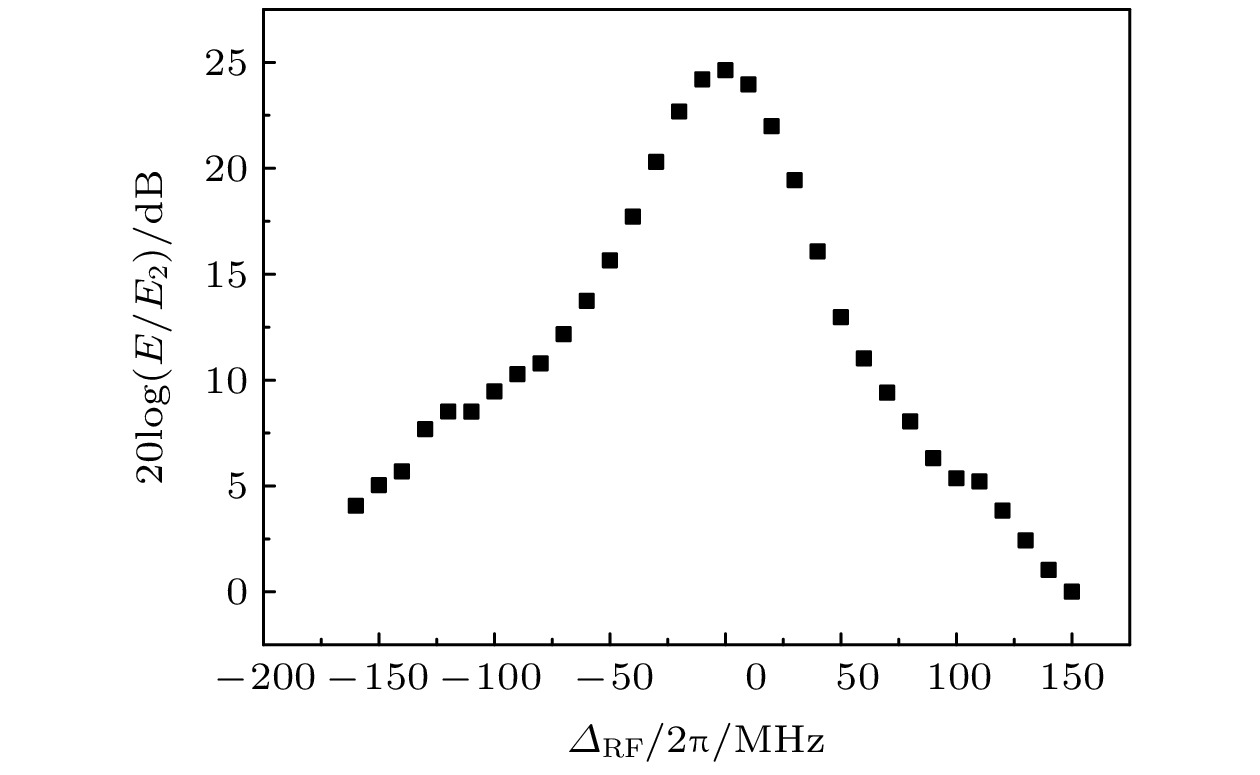
$\varDelta_{{\rm{RF}}}/2{\text{π}}$ = 30, 0, –15 MHz, respectively
图 5 传输带宽的测量. 改变信号微波场失谐, 测得不同失谐时的电平信号, 以电平最低(即
$\Delta_{RF}/2\pi = 150$ MHz)为零点归一化, 实现了调谐带宽大于200 MHz. 其中本地场强度为$E_{0} = 3.9$ mV/cm, 信号场强度为$E_{0}=1.7$ mV/cmFig. 5. Measurements of bandwidth. The obtained transmission bandwidth is larger than 200 MHz. Lock-in signal is normalized by minimum level (
$\varDelta_{\rm RF}/2\pi = 150$ MHz). The Local field strength is$E_{0}$ = 3.9 mV/cm and the signal field strength is$E_{0}$ = 1.7 mV/cm -
[1] Levanon N 1988 Radar Principles (New York: John Wiley & Sons) pp120−145
[2] Doviak R J, Zrnic D S 1993 Doppler Radar And Weather Observations (2nd Ed.) (New York: Academic Press) pp64−85
[3] Carr J J 1996 Microwave and Wireless Communications Technology (Newton: Butterworth-Heinemann) pp406−427
[4] Kanda M, Driver L D 1987 IEEE Trans. Antennas Propag. 35 33
Google Scholar
[5] Kanda M, Driver L D 1987 IEEE Trans. Microwave Theory Tech. 35 124
[6] Kanda M 1993 IEEE Trans. Antennas Propag. 41 1349
Google Scholar
[7] Stock M 2018 Meas. Tech. 60 1169
Google Scholar
[8] Gallagher T F 1994 Rydberg Atom (Cambridge: Cambridge University Press) pp11–47
[9] Jiao Y C, Hao L P, Han X X, Bai S Y, Raithel G, Zhao J M, Jia S T 2017 Phys. Rev. Appl. 8 014028
Google Scholar
[10] Harris S E 1997 Phys. Today 50 36
[11] Xiao M, Li Y Q, Jin S Z, Banacloche J G 1995 Phys. Rev. Lett. 74 666
Google Scholar
[12] Banacloche J G, Li Y Q, Jin S Z, Xiao M 1995 Phys. Rev. A 51 576
Google Scholar
[13] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003
Google Scholar
[14] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
Google Scholar
[15] Mohapatra A K, Bason M G, Butscher B, Weatherill K J, Adams C S 2008 Nat. Phys. 4 890
Google Scholar
[16] Autler S H, Townes C H 1955 Phys. Rev. 100 703
Google Scholar
[17] Cahuzac Ph, Vetter R 1976 Phys. Rev. A 14 270
Google Scholar
[18] Picqué J L, Pinard J 1976 J. Phys. B 9 L77
Google Scholar
[19] Kumar S, Fan H Q, Kübler H, Sheng J T, Shaffer J P 2017 Sci. Rep. 7 42981
Google Scholar
[20] Huang W, Liang Z T, Du Y X, Yan H, Zhu S L 2015 Acta Phys. Sin. 64 160702
Google Scholar
[21] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
Google Scholar
[22] Osterwalder A, Merkt F 1999 Phys. Rev. Lett. 82 1831
Google Scholar
[23] Downes L A, MacKellar A R, Whiting D J, Bourgenot C, Adams C S, Weatherill K J 2020 Phys. Rev. X 10 011027
Google Scholar
[24] Liao K Y, Tu H T, Yang S Z, Chen C J, Liu X H, Liang J, Zhang X D, Yan H, Zhu S L 2020 Phys. Rev. A 101 053432
Google Scholar
[25] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[26] Gordon J A, Simons M T, Haddab A H, Holloway C L 2019 AIP Adv. 9 045030
Google Scholar
[27] Hao L P, Xue Y M, Fan J B, Bai J X, Jiao Y C, Zhao J M 2020 Chin. Phys. B 29 033201
Google Scholar
[28] Deb A B, Kjærgaard N 2018 Appl. Phys. Lett. 112 211106
Google Scholar
[29] Meyer D H, Cox K C, Fatemi F K, Kunz P D 2018 Appl. Phys. Lett. 112 211108
Google Scholar
[30] Jiao Y C, Han X X, Fan J B, Georg R, Zhao J M, Jia S T 2019 Appl. Phys. Express 12 126002
Google Scholar
[31] Song Z F, Liu H P, Liu X C, Zhang W F, Zou H Y, Zhang J, Qu J F 2019 Opt. Express 27 8848
Google Scholar
[32] Anderson D A, Sapiro R E, Raithel G 2020 IEEE Trans. Antennas Propag. 10 1109
Google Scholar
[33] Holloway C L, Simons M T, Gordon J A, Novotny D 2019 IEEE Antennas Wirel. Propag. Lett. 18 1853
Google Scholar
[34] 樊佳蓓, 焦月春, 郝丽萍, 薛咏梅, 赵建明, 贾锁堂 2018 67 093201
Google Scholar
Fan J B, Jiao Y C, Hao L P, Xue Y M, Zhao J M, Jia S T 2018 Acta Phys. Sin. 67 093201
Google Scholar
[35] Bai J X, Fan J B, Hao L P, Spong N L R, Jiao Y C, Zhao J M 2019 Appl. Sci. 9 4895
Google Scholar
下载:
计量
- 文章访问数: 6524
- PDF下载量: 299
- 被引次数: 0
