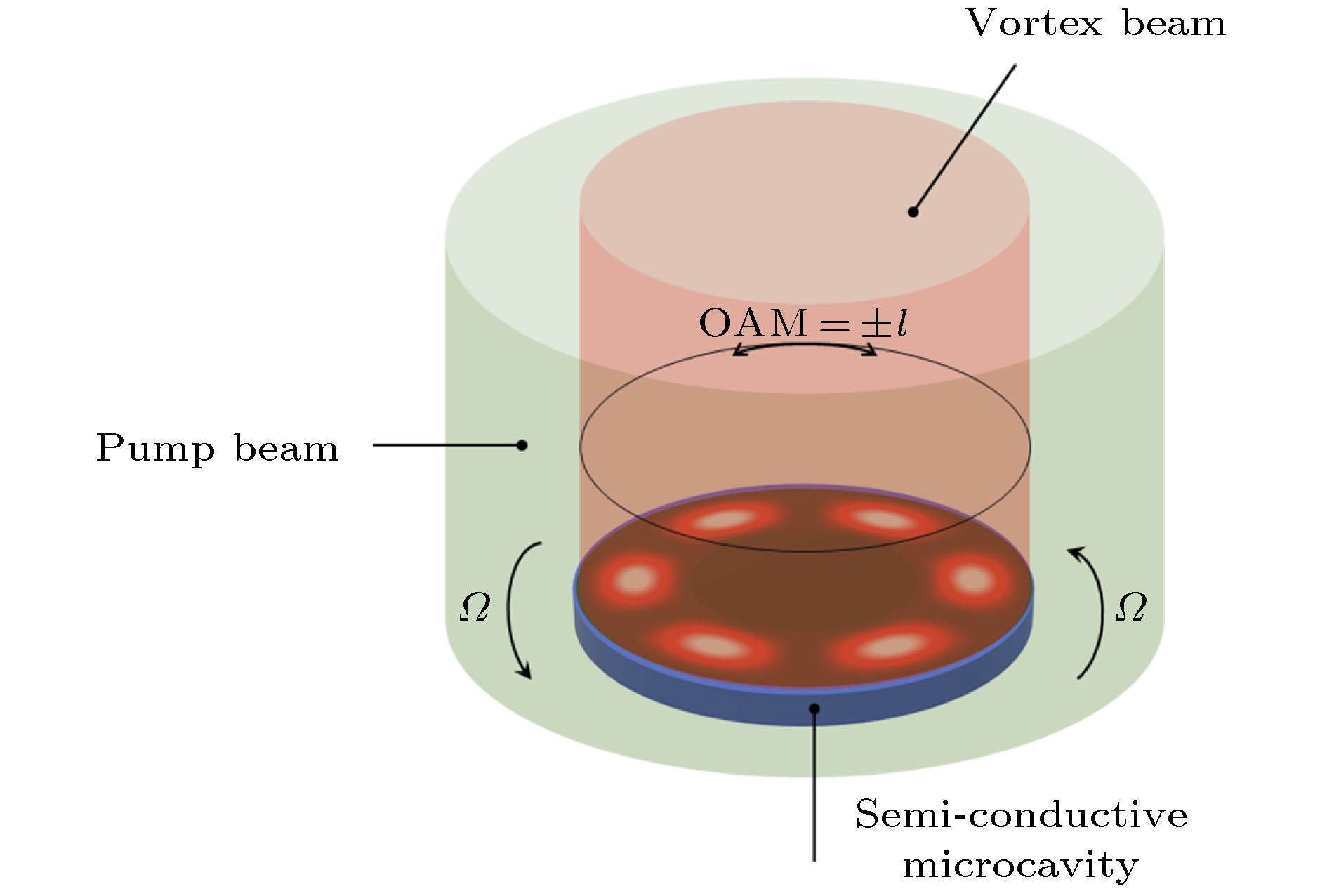
-
研究了二维激子极化激元凝聚正反涡旋叠加态在半导体微腔极化激元波色爱因斯坦凝聚(Bose–Einstein condensate, BEC)体系旋转情形下的稳定性和动力学特性. 在体系旋转情形下对单分量Gross-Pitaevskii方程进行重构, 利用四阶龙格库塔方法和时域有限差分方法构建数值模型. 利用实时演化方法研究在体系旋转的情况下, 不同拓扑荷数的正反涡旋叠加态的实时演化过程及稳态局域粒子数和体系旋转角速率之间的关系. 研究了涡旋叠加态激发区域的旋转速率与体系旋转速率的关系, 并阐明了体系的旋转速率对涡旋叠加态相位稳定性的影响机理.研究表明, 半导体微腔极化激元BEC体系的旋转速率对激子极化激元凝聚叠加态的演化过程及其动力学特性有重要影响.The gyroscope established on quantization vortices formed from exciton-polariton Bose-Einstein condensate has important potential applications in the field of quantum guidance. Thus, we assume a concept of quantum gyroscope based on Sagnac effect of the superposition states of quantum vortices existing in exciton-polariton condensates. To study the gyroscopic effect of superimposed vortices, which is the core issue of the project, it is essential to study the dynamic characteristics in the case of system rotating. Therefore, in this paper, the stability and dynamics of positive-negative vortex superposed states of two-dimensional exciton-polariton condensate in the disordered potential are studied under the rotation of the semiconductor microcavity, thereby laying a foundation for studying the gyroscopic effect of the superposed state of exciton-polariton condensates in the semiconductor microcavity. On the basis of reconstructing the mono-component Gross-Pitaevskii equation under the rotational situation, a numerical model with Coriolis items is constructed by the Runge-Kutta method and the finite difference time domain method, which is capable of depicting the rotation of the system. Moreover, the real-time evolution process of positive-negative vortex superposed states with different topological charges and the relationship between the number of steady-state local particles and the angular speed of the rotation of semiconductor microcavity are investigated by the real-time evolution method when the semiconductor microcavity is rotated. In the meantime, the relationship between the rotation speed in the excitation of vortex superposed states and the rotation speed of the semiconductor microcavity is also studied in the presence of the influence of the rotation speed of the semiconductor microcavity on the phase stability of vortex superposed states. According to the study, the rotation speed of the semiconductor microcavity has a significant influence on the evolution process and dynamic characteristics of vortex superposed states of exciton-polariton condensates. The rotation of the exciton-polariton system will accelerate the evolution of superimposed vortices, and overly rapid rotary rate will signalize the fluctuation of the local particle number thus the system unstability occurs. Moreover, along with the system rotation, the exciton-polariton superimposed vortices begin to rotate when the evolution approaches to saturation. It is noticeable that the angular acceleration of superimposed vortices is positively associated with the system rotary rate. Further, the topological charge has a significant influence on the rotation rate of exciation region of superposition state of vortices that it rotates more slowly when the topological charge increases but lower evolution stability simultaneously. These findings possess important guiding significance for establishing the quantum gyroscope in the future.
-
Keywords:
- quantum vortex gyroscope /
- exciton polariton /
- superposition state of vortices /
- rotational dynamics
[1] Zhang Y Y, Zou B 2012 Phys. Lett. A 376 3332
Google Scholar
[2] Shelykh I A, Rubo Y G, Kavokin A V 2007 Superlattices Microstruct. 41 313
Google Scholar
[3] Abdalla A S, Bingsuo Z, Ren Y, Liu T, Zhang Y Y 2018 Opt. Express 26 22273
Google Scholar
[4] 刘妮 2013 62 013402
Google Scholar
Liu N 2013 Acta Phys. Sin. 62 013402
Google Scholar
[5] 张用友, 金国钧 2009 物理 38 536
Zhang Y Y, Jin G J 2009 Physics 38 536 (in Chinese)
[6] 刘文楷, 安艳伟, 林世鸣 2005 光子学报 34 793
Google Scholar
Liu W K, An Y W, Lin S M, Zhang C S, Zhang C N 2005 Acta Photon. Sin. 34 793
Google Scholar
[7] Liu W K, Lin S M, An Y W 2004 J. Semicond. 025 1319
Google Scholar
[8] Lidzey D G, Bradley D D C, Skolnick M S, Virgili T, Walker S, Whittaker D M 1998 Nature 395 53
Google Scholar
[9] Kéna-Cohen S, Davanço M, Forrest S R 2008 Phys. Rev. Lett. 101 116401
Google Scholar
[10] Kéna-Cohen S, Forrest S R 2010 Nat. Photonics 4 371
Google Scholar
[11] Das A, Heo J, Jankowski M, Guo W, Zhang L, Deng H 2011 Phys. Rev. Lett. 107 227
Google Scholar
[12] Daskalakis K S, Maier S A, Murray R, S KénaCohen 2014 Nat. Mater. 13 271
Google Scholar
[13] Plumhof J D, Stöferle T, Mai L, Scherf U, Mahrt R F 2014 Nat. Mater. 13 247
Google Scholar
[14] Gao T, Estrecho E, Bliokh K Y, Liew T C H, Fraser M D, Brodbeck S 2015 Nature 526 554
Google Scholar
[15] Khan S, Türeci H E 2016 Phys. Rev. A 94 053856
Google Scholar
[16] Ma X, Berger B, Assmann M, Driben R, Meier T, Schneider C 2020 Nat. Commun. 11 897
Google Scholar
[17] Ma X K, Schumacher S 2017 Phys. Rev. B 95 235301
Google Scholar
[18] Chen T W, Hsieh W F, Cheng S C 2014 Frontiers in Optics 2014 Tucson, Arizona United States, October 19−23, 2014 pFW5C.4
[19] Iii F I M, Dowling J P, Dai W, Byrnes T 2015 Phys. Rev. A 93 053603
Google Scholar
[20] Kwon M S, Oh B Y, Gong S H, Kim J H, Kang H K, Kang S 2019 Phys. Rev. Lett. 122 045302
Google Scholar
[21] Zambon N C, St-Jean P, Lemaître A, Harouri A, Gratiet L L, Sagnes I 2018 Opt. Lett. 44 4531
Google Scholar
[22] 任元 中国专利 2016103181578 [2019-2-1]
Ren Y Chinese Patent 2016103181578 [2019-2-1] (in Chinese)
[23] Thanvanthri S, Kapalek K T, Dowling J P 2012 J. Mod. Opt. 59 1180
Google Scholar
[24] Padhi B, Duboscq R, Niranjan A, Soni R 2015 Eur. Phys. J. B 88 1
Google Scholar
[25] 陈海军, 任元, 王华 2019 原子与分子 36 124
Google Scholar
Chen H J, Ren Y, Wang H 2019 J. At. Mol. Phys. 36 124
Google Scholar
[26] 张用友 2009 博士学位论文 (南京: 南京大学)
Zhang Y Y 2009 Ph. D. Dissertation (Nanjing: Nanjing University) (in Chinese)
[27] Kartashov Y V, Zezyulin D A 2019 Opt. Lett. 44 4805
Google Scholar
-
图 1 旋转状态下的激子极化激元涡旋叠加态体系
Fig. 1. System of exciton polariton condensates on the rotational state.
图 2
$ l = \pm 2$ 时不同旋转角速率对激发场分布的影响 (a)$ \varOmega = 0$ ,$ t=80\hbar /{\rm{meV}}$ ; (b)$ \varOmega = 4.{\rm{0}} \times {10^{ - 7}}$ ,$ t=80\hbar /{\rm{meV}}$ ; (c)$\varOmega = 8.{\rm{0}} \times {10^{ - 7}}$ ,$ t=80\hbar /{\rm{meV}}$ ; (d)$ \varOmega = 1.2 \times {10^{ - {\rm{6}}}}$ ,$ t=80\hbar /{\rm{meV}}$ Fig. 2. Effects of different angular velocities of the rotation on the exciton field when
$l = \pm 2$ : (a)$\varOmega = 0$ ,$ t=80\hbar /{\rm{meV}}$ ; (b)$\varOmega = 4.{\rm{0}} \times {10^{ - 7}}$ ,$ t=80\hbar /{\rm{meV}}$ ; (c)$\varOmega = 8.{\rm{0}} \times {10^{ - 7}}$ ,$ t=80\hbar /{\rm{meV}}$ ; (d)$\varOmega = 1.2 \times {10^{ - {\rm{6}}}}$ ,$ t=80\hbar /{\rm{meV}}$ .
图 3 转动角速率与涡旋叠加态演化的关系 (a) 当
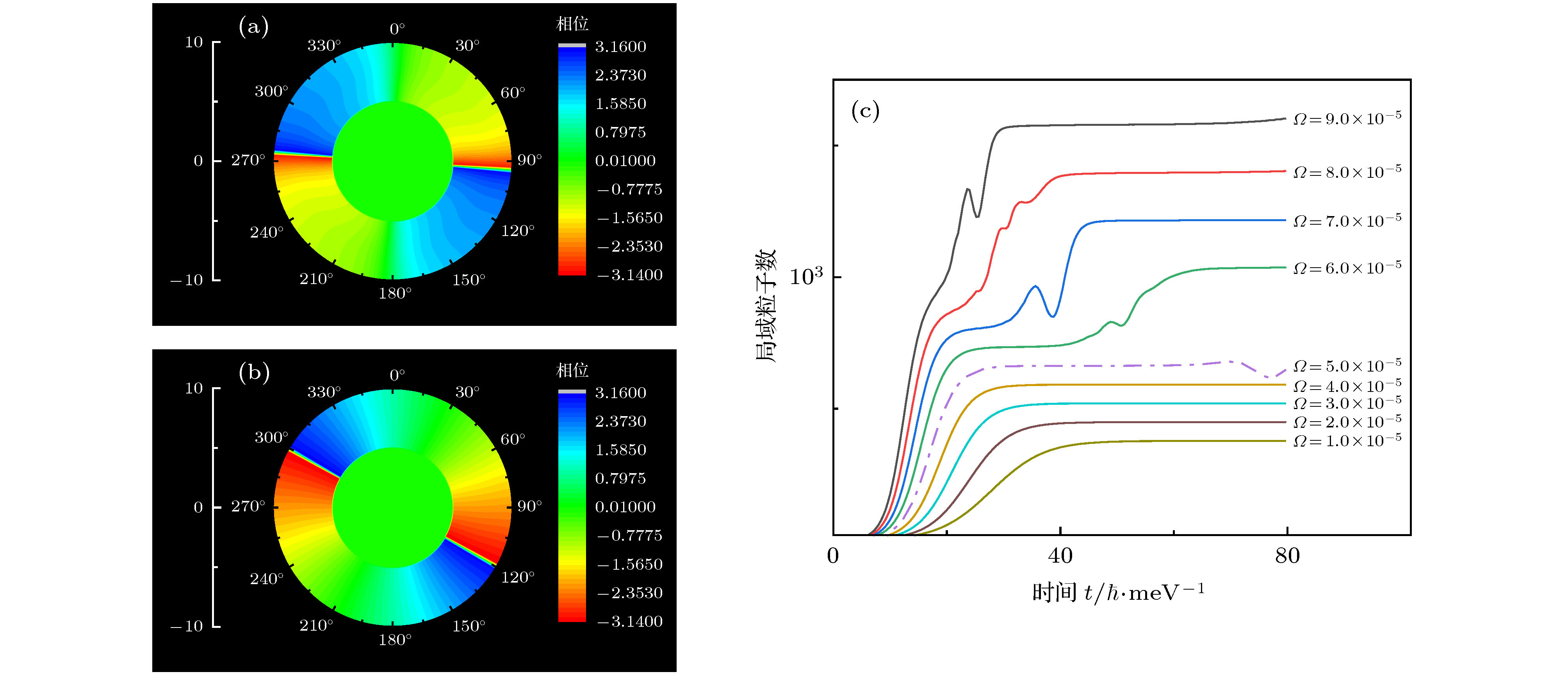
${\varOmega _1} = 1.{\rm{0}} \times {10^{ - 5}}$ ,$ t=80\hbar /{\rm{meV}}$ 时, 激子极化激元涡旋叠加态的相位分布; (b) 当${\varOmega _9} = {\rm{9}}.{\rm{0}} \times {10^{ - 5}}$ ,$ t=80\hbar /{\rm{meV}}$ 时, 激子极化激元涡旋叠加态的相位分布; (c) 当体系处于不同转速时激发区域内局域粒子数随时间的变化Fig. 3. The relationship between angular velocities of the rotation and the evolution of superposition state of vortexes: (a) The phase distribution of the superposition state of exciton polariton vortexes when
${\varOmega _1} = 1.{\rm{0}} \times {10^{ - 5}}$ and$ t=80\hbar /{\rm{meV}}$ ; (b) the phase distribution of superposition state of exciton polariton vortexes when${\varOmega _9} = {\rm{9}}.{\rm{0}} \times {10^{ - 5}}$ and$ t=80\hbar /{\rm{meV}}$ ; (c) the description curve of the relationship between time and quasi-particle number on various speeds of rotation of the system.
图 4 旋转状态下不同时刻的激子场分布 (a)
$ t=0\hbar /{\rm{meV}}$ ; (b)$ t=15\hbar /{\rm{meV}}$ ; (c)$ t=30\hbar /{\rm{meV}}$ ; (d)$ t=45\hbar /{\rm{meV}}$ ; (e)$t= 60\hbar /{\rm{meV}}$ ; (f)$ t=75\hbar /{\rm{meV}}$ Fig. 4. The exciton field distribution at different moments in the rotational state: (a)
$ t=0\hbar /{\rm{meV}}$ ; (b)$ t=15\hbar /{\rm{meV}}$ ; (c)$t= 30\hbar /{\rm{meV}}$ ; (d)$ t=45\hbar /{\rm{meV}}$ ; (e) t$t= 60\hbar /{\rm{meV}}$ ; (f)$ t=75\hbar /{\rm{meV}}$ .
图 5 激子极化激元涡旋叠加态瞬时转动角速率与体系转速的关系
Fig. 5. The relationship between the instantaneous angular rate of the superposition state of exciton polariton vortexes and the rotate speed of the system.
图 6 转动角速率对不同拓扑荷数激子极化激元涡旋叠加态的影响 (a)体系旋转角速率
$\varOmega \in (2.{\rm{0}} \times {{10}^{ - 7}}, 1.{\rm{0}} \times {{10}^{ - 6}})$ , t = 80ћ/meV时刻, 拓扑荷数分别为$l = \pm 4$ 和$l = \pm 12$ 的涡旋叠加态相对于初态转过的角度; (b)不同拓扑荷数情况下, 体系旋转角速率对演化过程产生的影响Fig. 6. Effects of the angular velocities on the superposition state of exciton polariton vortexes with different topological charge number: (a) Angle of rotation of superposition state vortexes to the initial state at the moment of t = 80ћ/meV with different topological charge of
$l = \pm 4$ and$l = \pm 12$ in the angular rate range of$\varOmega \in (2.{\rm{0}} \times {{10}^{ - 7}}, 1.{\rm{0}} \times {{10}^{ - 6}} )$ ; (b) effect of the system angular rate on the evolution process with different topological charges. -
[1] Zhang Y Y, Zou B 2012 Phys. Lett. A 376 3332
Google Scholar
[2] Shelykh I A, Rubo Y G, Kavokin A V 2007 Superlattices Microstruct. 41 313
Google Scholar
[3] Abdalla A S, Bingsuo Z, Ren Y, Liu T, Zhang Y Y 2018 Opt. Express 26 22273
Google Scholar
[4] 刘妮 2013 62 013402
Google Scholar
Liu N 2013 Acta Phys. Sin. 62 013402
Google Scholar
[5] 张用友, 金国钧 2009 物理 38 536
Zhang Y Y, Jin G J 2009 Physics 38 536 (in Chinese)
[6] 刘文楷, 安艳伟, 林世鸣 2005 光子学报 34 793
Google Scholar
Liu W K, An Y W, Lin S M, Zhang C S, Zhang C N 2005 Acta Photon. Sin. 34 793
Google Scholar
[7] Liu W K, Lin S M, An Y W 2004 J. Semicond. 025 1319
Google Scholar
[8] Lidzey D G, Bradley D D C, Skolnick M S, Virgili T, Walker S, Whittaker D M 1998 Nature 395 53
Google Scholar
[9] Kéna-Cohen S, Davanço M, Forrest S R 2008 Phys. Rev. Lett. 101 116401
Google Scholar
[10] Kéna-Cohen S, Forrest S R 2010 Nat. Photonics 4 371
Google Scholar
[11] Das A, Heo J, Jankowski M, Guo W, Zhang L, Deng H 2011 Phys. Rev. Lett. 107 227
Google Scholar
[12] Daskalakis K S, Maier S A, Murray R, S KénaCohen 2014 Nat. Mater. 13 271
Google Scholar
[13] Plumhof J D, Stöferle T, Mai L, Scherf U, Mahrt R F 2014 Nat. Mater. 13 247
Google Scholar
[14] Gao T, Estrecho E, Bliokh K Y, Liew T C H, Fraser M D, Brodbeck S 2015 Nature 526 554
Google Scholar
[15] Khan S, Türeci H E 2016 Phys. Rev. A 94 053856
Google Scholar
[16] Ma X, Berger B, Assmann M, Driben R, Meier T, Schneider C 2020 Nat. Commun. 11 897
Google Scholar
[17] Ma X K, Schumacher S 2017 Phys. Rev. B 95 235301
Google Scholar
[18] Chen T W, Hsieh W F, Cheng S C 2014 Frontiers in Optics 2014 Tucson, Arizona United States, October 19−23, 2014 pFW5C.4
[19] Iii F I M, Dowling J P, Dai W, Byrnes T 2015 Phys. Rev. A 93 053603
Google Scholar
[20] Kwon M S, Oh B Y, Gong S H, Kim J H, Kang H K, Kang S 2019 Phys. Rev. Lett. 122 045302
Google Scholar
[21] Zambon N C, St-Jean P, Lemaître A, Harouri A, Gratiet L L, Sagnes I 2018 Opt. Lett. 44 4531
Google Scholar
[22] 任元 中国专利 2016103181578 [2019-2-1]
Ren Y Chinese Patent 2016103181578 [2019-2-1] (in Chinese)
[23] Thanvanthri S, Kapalek K T, Dowling J P 2012 J. Mod. Opt. 59 1180
Google Scholar
[24] Padhi B, Duboscq R, Niranjan A, Soni R 2015 Eur. Phys. J. B 88 1
Google Scholar
[25] 陈海军, 任元, 王华 2019 原子与分子 36 124
Google Scholar
Chen H J, Ren Y, Wang H 2019 J. At. Mol. Phys. 36 124
Google Scholar
[26] 张用友 2009 博士学位论文 (南京: 南京大学)
Zhang Y Y 2009 Ph. D. Dissertation (Nanjing: Nanjing University) (in Chinese)
[27] Kartashov Y V, Zezyulin D A 2019 Opt. Lett. 44 4805
Google Scholar
下载:
计量
- 文章访问数: 5863
- PDF下载量: 94
- 被引次数: 0
