-
神经元的自突触结构具有自反馈的作用, 神经递质量子形式的释放使得自突触的自反馈作用容易受到扰动, 本文重点研究了化学自突触的电导扰动对FHN神经元电生理活动的影响. 首先, 恰当的化学自突触参数能够产生动力学行为的分岔现象, 诱导不同周期峰放电模式之间的转迁. 特别地, 自突触的自反馈功能会引起从混沌放电状态到周期的峰放电或准周期的簇放电状态的转迁. 其次, 基于神经递质释放的量子特征, 借助放电频率和变异系数两个指标定量地研究自突触电导的随机扰动对神经元放电活动的影响. 数值结果表明自突触电导的扰动在自反馈的作用下能够改变离子通道的活性, 不仅提高FHN神经元对外加激励信号的编码效率, 而且改变神经元放电活动的规则性, 诱导显著的相干或随机双共振现象, 其内在机制是电导扰动所引起的神经元系统不稳定的动力学分岔. 本文的研究进一步揭示了自突触结构对神经元放电活动自我调节的作用, 有待为生理操控自突触结构提供理论参考.The autaptic structure of neurons has the function of self-feedback, which is easily disturbed due to the quantum characteristics of neurotransmitter release. This paper focuses on the effect of conductance disturbance of chemical autapse on the electrophysiological activities of FHN neuron. First, the frequency encoding of FHN neuron to periodic excitation signals exhibits a nonlinear change characteristic, and the FHN neuron without autapse has chaotic discharge behavior according to the maximum Lyapunov exponent and the sampled time series. Secondly, the chemical autaptic function can change the dynamics of FHN neuronal system, and appropriate autaptic parameters can cause the dynamic bifurcation, which corresponds to the transition between different periodic spiking modes. In particular, the self-feedback function of chemical autapse can induce a transition from a chaotic discharge state to a periodic spiking or a quasi-periodic bursting discharge state. Finally, based on the quantum characteristics of neurotransmitter release, the effect of random disturbance from autaptic conductance on the firing activities is quantitatively studied with the help of the discharge frequency and the coefficient of variation of inter-spike interval series. The numerical results show that the disturbance of autaptic conductance can change the activity of ion channels under the action of self-feedback, which not only improves the encoding efficiency of FHN neuron to external excitation signals, but also changes the regularity of neuronal firing activities and induces significant coherent or stochastic bi-resonance. The coherent or stochastic bi-resonance phenomenon is closely related to the dynamic bifurcation of FitzHugh-Nagumo(FHN) neuronal system, and its underlying mechanism is that the disturbance of autaptic conductance leads to the unstable dynamic behavior of neuronal system, and the corresponding neuronal firing activity may transit between the resting state, the single-cycle and the multicycle spike states, thereby providing the occurring possibility for coherent or stochastic bi-resonance. This study further reveals the self-regulatory effect of the autaptic structure on neuronal firing activities, and could provide theoretical guidance for physiological manipulation of autapses. In addition, according to the pronounced self-feedback function of autaptic structure, a recurrent spiking neural network with local self-feedback can be constructed to improve the performance of machine learning by applying a synaptic plasticity rule.
-
Keywords:
- chemical autapse /
- conductance disturbance /
- bifurcation /
- bi-resonance
[1] van der Loos H, Glaser E M 1972 Brain Res. 48 355
Google Scholar
[2] Wang H T, Chen Y 2015 Chin. Phys. B 24 128709
Google Scholar
[3] Lübke J, Markram H, Frotscher M, Sakmann B 1996 J. Neurosci. 16 3209
Google Scholar
[4] Wang C N, Guo S L, Xu Y, Ma J, Tang J, Alzahrani F, Hobiny A 2017 Complexity 2017 5436737
Google Scholar
[5] Li Y Y, Schmid G, Hänggi P, Schimansky-Geier L 2010 Phys. Rev. E 82 061907
Google Scholar
[6] 华洪涛, 陆博, 古华光 2020 69 090502
Google Scholar
Hua H T, Lu B, Gu H G 2020 Acta Phys. Sin. 69 090502
Google Scholar
[7] Hashemi M, Valizadeh A, Azizi Y 2012 Phys. Rev. E 85 021917
Google Scholar
[8] Qu L H, Du L, Deng Z C, Cao Z L, Hu H W 2018 Chin. Phys. B 27 118707
Google Scholar
[9] Bekkers J M 2003 Curr. Biol. 13 433
Google Scholar
[10] Xu Y, Ying H P, Jia Y, Ma J, Hayat T 2017 Sci. Rep. 7 43452
Google Scholar
[11] Guo D Q, Chen M M, Perc M, Wu S D, Xia C, Zhang Y S, Xu P, Xia Y, Yao D Z 2016 Europhys. Lett. 114 30001
Google Scholar
[12] Zhao Z G, Li L, Gu H G 2020 Commun. Nonlinear Sci. Numer. Simulat. 85 105250
Google Scholar
[13] Ren G D, Zhou P, Ma J, Cai N, Alsaedi A, Ahmad B 2017 Int. J. Bifurcat. Chaos 27 1750187
Google Scholar
[14] Song X L, Wang H T, Chen Y 2018 Nonlinear Dyn. 94 141
Google Scholar
[15] Yilmaz E, Ozer M, Baysal V, Perc M 2016 Sci. Rep. 6 30914
Google Scholar
[16] Wang H T, Wang L F, Chen Y L, Chen Y 2014 Chaos 24 033122
Google Scholar
[17] Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760
Google Scholar
[18] Yue Y, Liu L W, Liu Y J, Chen Y, Chen Y L, Yu L C 2017 Nonlinear Dyn. 90 2893
Google Scholar
[19] Ma J, Song X L, Jin W Y, Wang C N 2015 Chaos Soliton. Fract. 80 31
Google Scholar
[20] Wu Y N, Gong Y B, Wang Q 2015 Chaos 25 043113
Google Scholar
[21] Kim Y 2017 J. Korean Phys. Soc. 71 63
Google Scholar
[22] Wiles L, Gu S, Pasqualetti F, Parvesse B, Gabrieli D, Bassett D S, Meaney D F 2017 Sci. Rep. 7 44006
Google Scholar
[23] Mao X C 2018 Int. J. Bifurcat. Chaos 28 1850071
Google Scholar
[24] Ma J, Song X L, Tang J, Wang C N 2015 Neurocomputing 167 378
Google Scholar
[25] 黄志精, 李倩昀, 白婧, 唐国宁 2019 68 110503
Google Scholar
Huang Z J, Li Q Y, Bai J, Tang G N 2019 Acta Phys. Sin. 68 110503
Google Scholar
[26] Wang R, Li J J, Du M M, Lei J Z, Wu Y 2016 Commun. Nonlinear Sci. Numer. Simulat. 40 80
Google Scholar
[27] Wang Q Y, Perc M, Duan Z S, Chen G R 2009 Phys. Rev. E 80 026206
Google Scholar
[28] Qin H X, Ma J, Wang C N, Wu Y 2014 PLoS One 9 e100849
Google Scholar
[29] Qin H X, Ma J, Wang C N, Chu R T 2014 Sci. China Phys. Mech. 57 1918
Google Scholar
[30] Ma J, Tang J 2017 Nonlinear Dyn. 89 1569
Google Scholar
[31] Yang X L, Yu Y H, Sun Z K 2017 Chaos 27 083117
Google Scholar
[32] Yilmaz E, Baysal V, Perc M, Ozer M 2016 Sci. China Technol. Sci. 59 364
Google Scholar
[33] 李国芳, 孙晓娟 2017 66 240501
Google Scholar
Li G F, Sun X J 2017 Acta Phys. Sin. 66 240501
Google Scholar
[34] Xie H J, Gong Y B, Wang B Y 2018 Chaos Soliton. Fract. 108 1
Google Scholar
[35] Yilmaz E, Baysal V, Ozer M, Perc M 2016 Physica A 444 538
Google Scholar
[36] Xu Y, Jia Y, Kirunda J B, Shen J, Ge M Y, Lu L L, Pei Q M 2018 Complexity 2018 3012743
Google Scholar
[37] Fan H W, Wang Y F, Wang H T, Lai Y C, Wang X G 2018 Sci. Rep. 8 580
Google Scholar
[38] Qu L H, Du L, Zhang H H, Cao Z L, Deng Z C 2019 Int. J. Bifurcat. Chaos 29 1950202
Google Scholar
[39] Izhikevich E M, FitzHugh R 2006 Scholarpedia 1 1349
Google Scholar
[40] Izhikevich E M 2007 Dynamical Systems in Neuroscience: the Geometry of Excitability and Bursting (Cambridge: MIT Press) p106
[41] Shipshina M S, Veselovsky N S, Fedulova S A 2009 Neurophysiology 41 165
Google Scholar
[42] Georgiev D D, Glazebrook J F 2018 Prog. Biophys. Mol. Bio. 135 16
Google Scholar
[43] Branco T, Staras K 2009 Nat. Rev. Neurosci. 10 373
Google Scholar
[44] Valenti O, Cifelli P, Gill K M, Grace A A 2011 J. Neurosci. 31 12330
Google Scholar
[45] Jia B, Gu H G 2017 Int. J. Bifurcat. Chaos 27 1750113
Google Scholar
[46] Goldwyn J H, Shea-Brown E 2011 PLoS Comput. Biol. 7 e1002247
Google Scholar
[47] Du L, Cao Z L, Lei Y M, Deng Z C 2019 Sci. China Technol. Sci. 62 1141
Google Scholar
[48] Honeycutt R L 1992 Phys. Rev. A 45 600
Google Scholar
-
图 1 FHN神经元系统的脉冲放电频率(a)及其最大Lyapunov指数(b)对周期振荡的外加激励的依赖关系示意图, 其中(b)中周期激励的振幅为
$A = 0.6$ Fig. 1. Dependence of (a) spike discharge frequency and (b) maximum Lyapunov exponent on external periodic excitation, where the amplitudes of periodic excitation are
$A = 0.6$ in the subfigure (b).
图 2 外加周期激励的作用下FHN神经元放电活动的时间历程图 (a)
$A = 0.6$ ,$f = 1.0$ ; (b)$A = 0.6$ ,$f = 29.0$ Fig. 2. Sampled time series of neuronal membrane potentials under different periodic excitation: (a)
$A = 0.6$ ,$f = 1.0$ ; (b)$A = 0.6$ ,$f = 29.0$ .
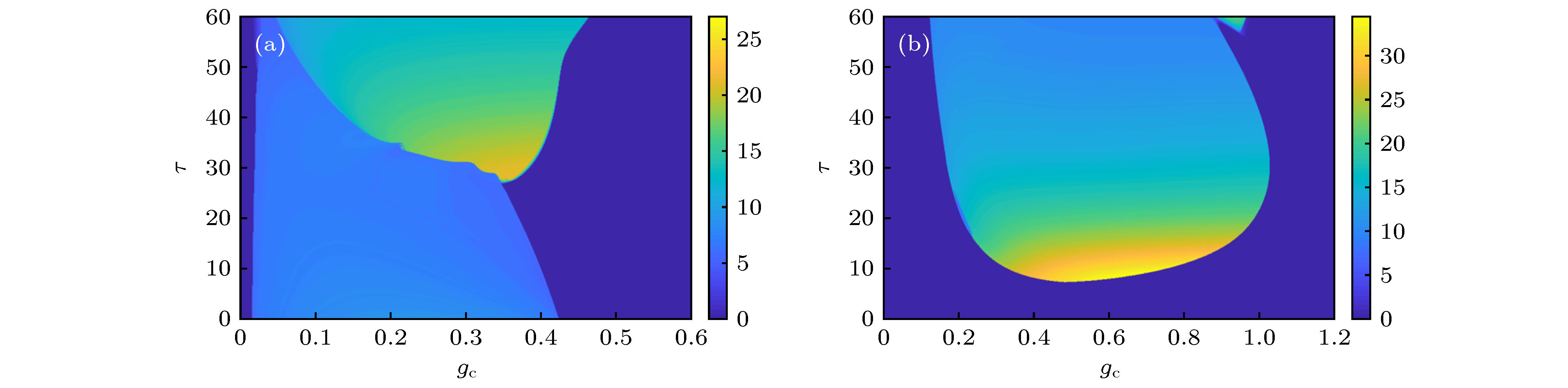
图 3 不同外加激励和突触反转电位条件下FHN神经元脉冲放电的频率对自突触功能两个参数的依赖关系示意图 (a)
${I_{{\rm{ext}}}} = 0.05$ ,${V_{{\rm{syn}}}} = 1.2$ ; (b)${I_{{\rm{ext}}}} = 0.6$ ,${V_{{\rm{syn}}}} = - 0.2$ Fig. 3. Dependence of spike discharge frequency of FHN neurons on two autaptic parameters under different applied excitation and synaptic reversal potential: (a)
${I_{{\rm{ext}}}} = 0.05$ ,${V_{{\rm{syn}}}} = 1.2$ ; (b)${I_{{\rm{ext}}}} = 0.6$ ,${V_{{\rm{syn}}}} = - 0.2$ .
图 4 FHN神经元脉冲放电的峰峰间期对不同的自突触结构参数的依赖关系示意图 (a)
${I_{{\rm{ext}}}} = 0.05$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (b)${I_{{\rm{ext}}}} = 0.05$ ,${g_{\rm{c}}} = 0.3$ ,${V_{{\rm{syn}}}} = 1.2$ ; (c)${I_{{\rm{ext}}}} = 0.6$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = - 0.2$ ; (d)${I_{{\rm{ext}}}} = 0.6$ ,${g_{\rm{c}}} = 0.3$ ,${V_{{\rm{syn}}}} = - 0.2$ Fig. 4. Dependence of neuronal firing inter-spike intervals on different autaptic parameters: (a)
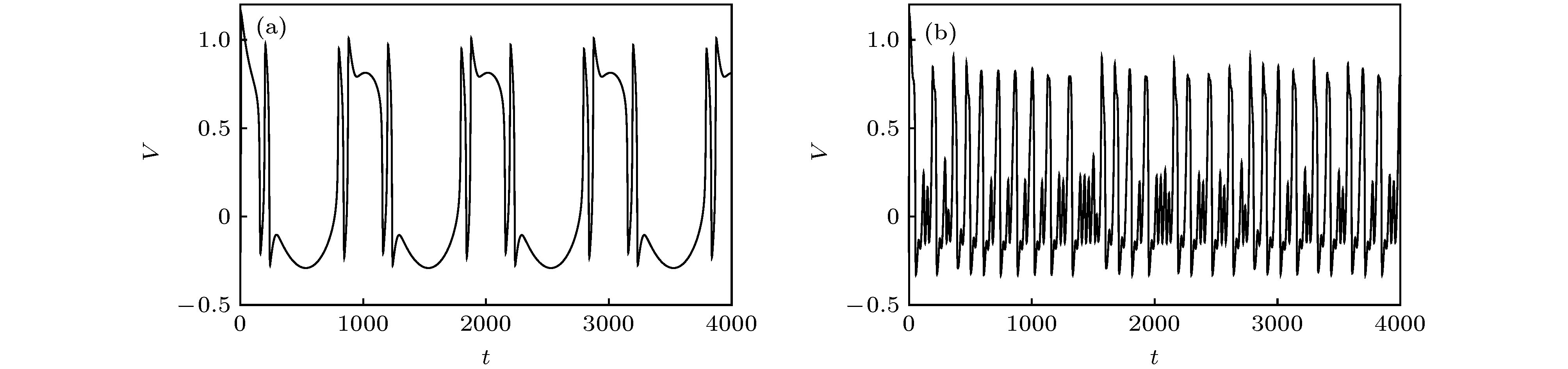
${I_{{\rm{ext}}}} = 0.05$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (b)${I_{{\rm{ext}}}} = 0.05$ ,${g_{\rm{c}}} = 0.3$ ,${V_{{\rm{syn}}}} = 1.2$ ; (c)${I_{{\rm{ext}}}} = 0.6$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = - 0.2$ ; and (d)${I_{{\rm{ext}}}} = 0.6$ ,${g_{\rm{c}}} = 0.3$ ,${V_{{\rm{syn}}}} = - 0.2$ .
图 5 具有自突触结构的FHN神经元放电活动的时间历程图, 其中自突触参数
${g_{\rm{c}}} = 0.3$ ,$\tau = 30.0$ , 且自突触功能在$t = 300$ 时被激活 (a)$A = 0.05$ ,$f = 0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (b)$A = 0.6$ ,$f = 0$ ,${V_{{\rm{syn}}}} = - 0.2$ ; (c)$A = 0.6$ ,$f = 16.0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (d)$A = 0.6$ ,$f = 29.0$ ,${V_{{\rm{syn}}}} = 1.2$ Fig. 5. Sampled time series of neuronal membrane potentials under excitatory or inhibitory autaptic function, where
${g_{\rm{c}}} = 0.3$ ,$\tau = 30.0$ , and the autaptic function is activated at$t = 300$ : (a)$A = 0.05$ ,$f = 0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (b)$A = 0.6$ ,$f = 0$ ,${V_{{\rm{syn}}}} = - 0.2$ ; (c)$A = 0.6$ ,$f = 16.0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (d)$A = 0.6$ ,$f = 29.0$ ,${V_{{\rm{syn}}}} = 1.2$ .
图 6 在自突触电导随机扰动的作用下FHN神经元的放电频率和峰峰间期序列的变异系数对噪声强度的依赖关系示意图 (a), (b)
$A = 0.05$ ,$f = 0$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (c), (d)$A = 0.05$ ,$f = 10.0$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ Fig. 6. Dependence of spike discharge frequency and coefficient of variation on noise intensity under disturbance of autaptic conductance, where (a), (b)
$A = 0.05$ ,$f = 0$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ ; (c), (d)$A = 0.05$ ,$f = 10.0$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ .
图 7 具有自突触结构的FHN神经元放电活动的时间历程图, 其中
$A = 0.05$ ,$f = 10.0$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ , 且自突触功能在$t = 300$ 时被激活 (a)${g_{\rm{c}}} = 0.037$ ,$D = 0.0001$ ; (b)${g_{\rm{c}}} = 0.037$ ,$D = 0.016$ ; (c)${g_{\rm{c}}} = 0.448$ ,$D = 0.0007$ ; (d)${g_{\rm{c}}} = 0.448$ , D = 0.005Fig. 7. Sampled time series of neuronal membrane potentials under autaptic function, where
$A = 0.05$ ,$f = 10.0$ ,$\tau = 30.0$ ,${V_{{\rm{syn}}}} = 1.2$ , and the autaptic function is activated at$t = 300$ : (a)${g_{\rm{c}}} = 0.037$ ,$D = 0.0001$ ; (b)${g_{\rm{c}}} = 0.037$ ,$D = 0.016$ ; (c)${g_{\rm{c}}} = 0.448$ ,$D = 0.0007$ ; (d)${g_{\rm{c}}} = 0.448$ ,$D = 0.005$ . -
[1] van der Loos H, Glaser E M 1972 Brain Res. 48 355
Google Scholar
[2] Wang H T, Chen Y 2015 Chin. Phys. B 24 128709
Google Scholar
[3] Lübke J, Markram H, Frotscher M, Sakmann B 1996 J. Neurosci. 16 3209
Google Scholar
[4] Wang C N, Guo S L, Xu Y, Ma J, Tang J, Alzahrani F, Hobiny A 2017 Complexity 2017 5436737
Google Scholar
[5] Li Y Y, Schmid G, Hänggi P, Schimansky-Geier L 2010 Phys. Rev. E 82 061907
Google Scholar
[6] 华洪涛, 陆博, 古华光 2020 69 090502
Google Scholar
Hua H T, Lu B, Gu H G 2020 Acta Phys. Sin. 69 090502
Google Scholar
[7] Hashemi M, Valizadeh A, Azizi Y 2012 Phys. Rev. E 85 021917
Google Scholar
[8] Qu L H, Du L, Deng Z C, Cao Z L, Hu H W 2018 Chin. Phys. B 27 118707
Google Scholar
[9] Bekkers J M 2003 Curr. Biol. 13 433
Google Scholar
[10] Xu Y, Ying H P, Jia Y, Ma J, Hayat T 2017 Sci. Rep. 7 43452
Google Scholar
[11] Guo D Q, Chen M M, Perc M, Wu S D, Xia C, Zhang Y S, Xu P, Xia Y, Yao D Z 2016 Europhys. Lett. 114 30001
Google Scholar
[12] Zhao Z G, Li L, Gu H G 2020 Commun. Nonlinear Sci. Numer. Simulat. 85 105250
Google Scholar
[13] Ren G D, Zhou P, Ma J, Cai N, Alsaedi A, Ahmad B 2017 Int. J. Bifurcat. Chaos 27 1750187
Google Scholar
[14] Song X L, Wang H T, Chen Y 2018 Nonlinear Dyn. 94 141
Google Scholar
[15] Yilmaz E, Ozer M, Baysal V, Perc M 2016 Sci. Rep. 6 30914
Google Scholar
[16] Wang H T, Wang L F, Chen Y L, Chen Y 2014 Chaos 24 033122
Google Scholar
[17] Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760
Google Scholar
[18] Yue Y, Liu L W, Liu Y J, Chen Y, Chen Y L, Yu L C 2017 Nonlinear Dyn. 90 2893
Google Scholar
[19] Ma J, Song X L, Jin W Y, Wang C N 2015 Chaos Soliton. Fract. 80 31
Google Scholar
[20] Wu Y N, Gong Y B, Wang Q 2015 Chaos 25 043113
Google Scholar
[21] Kim Y 2017 J. Korean Phys. Soc. 71 63
Google Scholar
[22] Wiles L, Gu S, Pasqualetti F, Parvesse B, Gabrieli D, Bassett D S, Meaney D F 2017 Sci. Rep. 7 44006
Google Scholar
[23] Mao X C 2018 Int. J. Bifurcat. Chaos 28 1850071
Google Scholar
[24] Ma J, Song X L, Tang J, Wang C N 2015 Neurocomputing 167 378
Google Scholar
[25] 黄志精, 李倩昀, 白婧, 唐国宁 2019 68 110503
Google Scholar
Huang Z J, Li Q Y, Bai J, Tang G N 2019 Acta Phys. Sin. 68 110503
Google Scholar
[26] Wang R, Li J J, Du M M, Lei J Z, Wu Y 2016 Commun. Nonlinear Sci. Numer. Simulat. 40 80
Google Scholar
[27] Wang Q Y, Perc M, Duan Z S, Chen G R 2009 Phys. Rev. E 80 026206
Google Scholar
[28] Qin H X, Ma J, Wang C N, Wu Y 2014 PLoS One 9 e100849
Google Scholar
[29] Qin H X, Ma J, Wang C N, Chu R T 2014 Sci. China Phys. Mech. 57 1918
Google Scholar
[30] Ma J, Tang J 2017 Nonlinear Dyn. 89 1569
Google Scholar
[31] Yang X L, Yu Y H, Sun Z K 2017 Chaos 27 083117
Google Scholar
[32] Yilmaz E, Baysal V, Perc M, Ozer M 2016 Sci. China Technol. Sci. 59 364
Google Scholar
[33] 李国芳, 孙晓娟 2017 66 240501
Google Scholar
Li G F, Sun X J 2017 Acta Phys. Sin. 66 240501
Google Scholar
[34] Xie H J, Gong Y B, Wang B Y 2018 Chaos Soliton. Fract. 108 1
Google Scholar
[35] Yilmaz E, Baysal V, Ozer M, Perc M 2016 Physica A 444 538
Google Scholar
[36] Xu Y, Jia Y, Kirunda J B, Shen J, Ge M Y, Lu L L, Pei Q M 2018 Complexity 2018 3012743
Google Scholar
[37] Fan H W, Wang Y F, Wang H T, Lai Y C, Wang X G 2018 Sci. Rep. 8 580
Google Scholar
[38] Qu L H, Du L, Zhang H H, Cao Z L, Deng Z C 2019 Int. J. Bifurcat. Chaos 29 1950202
Google Scholar
[39] Izhikevich E M, FitzHugh R 2006 Scholarpedia 1 1349
Google Scholar
[40] Izhikevich E M 2007 Dynamical Systems in Neuroscience: the Geometry of Excitability and Bursting (Cambridge: MIT Press) p106
[41] Shipshina M S, Veselovsky N S, Fedulova S A 2009 Neurophysiology 41 165
Google Scholar
[42] Georgiev D D, Glazebrook J F 2018 Prog. Biophys. Mol. Bio. 135 16
Google Scholar
[43] Branco T, Staras K 2009 Nat. Rev. Neurosci. 10 373
Google Scholar
[44] Valenti O, Cifelli P, Gill K M, Grace A A 2011 J. Neurosci. 31 12330
Google Scholar
[45] Jia B, Gu H G 2017 Int. J. Bifurcat. Chaos 27 1750113
Google Scholar
[46] Goldwyn J H, Shea-Brown E 2011 PLoS Comput. Biol. 7 e1002247
Google Scholar
[47] Du L, Cao Z L, Lei Y M, Deng Z C 2019 Sci. China Technol. Sci. 62 1141
Google Scholar
[48] Honeycutt R L 1992 Phys. Rev. A 45 600
Google Scholar
下载:
计量
- 文章访问数: 6167
- PDF下载量: 132
- 被引次数: 0
