激子极化激元凝聚体中的二维亮孤子

黄轶凡; 梁兆新

doi:10.7498/aps.72.20230425

摘要

在非保守非线性系统中, 产生孤子的基本物理机理是系统的动能与非线性、以及增益与耗散达到双动力学平衡. 如何在该系统中产生稳定的自由高维孤子是目前孤子理论具有挑战性的前沿课题. 本文提出了一种在激子极化激元玻色-爱因斯坦凝聚体中实现二维自由亮孤子理论方案, 即通过时间周期调制相互作用以及增益与耗散双平衡的物理机理产生稳定的二维自由空间亮孤子. 为此, 首先通过拉格朗日量变分法得到了二维亮孤子参数的动力学方程, 得到其动力学稳定的参数空间. 其次, 数值模拟广义增益耗散Gross-Pitaveskii方程的含时演化, 验证了二维亮孤子的稳定性. 最后, 加入高斯噪声模拟真实实验环境, 发现在实验可观测的时间范围内, 二维亮孤子是稳定的. 本文的实验方案打开了在非保守系统中研究高维自由空间亮孤子的大门.

关键词:

Abstract

In non-conservative nonlinear systems, the basic physical mechanics of soliton generation is that the kinetic energy and nonlinear terms of the system, as well as the gain and dissipation terms reach a double dynamic balance. How to generate stable free high-dimensional solitons in such a system is currently a challenging topic in soliton theory. In this article, we propose a theoretical scheme for realizing two-dimensional free bright solitons in exciton-polariton Bose-Einstein condensates, which proposes a physical mechanism for generating stable two-dimensional free space bright solitons through time periodic modulation interactions and a dual balance between gain and dissipation. In this end, firstly, we obtain the dynamic equations of two-dimensional bright soliton parameters through the Lagrange variational method, and obtain its dynamically stable parameter space. Secondly, the evolution of the generalized dissipative Gross-Pitaveskii equation is numerically simulated to verify the stability of two-dimensional bright solitons. Finally, we add Gaussian noise to simulate a real experimental environment and find that two-dimensional bright solitons are also stable within the observable time range of the experiment. Our experimental scheme opens the door to the study of bright solitons in high-dimensional free space in non-conservative systems.

Keywords:

作者及机构信息

浙江师范大学物理系, 金华　321004

通信作者: 梁兆新, zhxliang@zjnu.edu.cn

基金项目: 浙江省自然科学基金重点项目(批准号: LZ21A040001)和国家自然科学基金(批准号: 12074344)资助的课题

Authors and contacts

Department of Physics, Zhejiang Normal University, Jinhua 321004, China

Corresponding author: Liang Zhao-Xin, zhxliang@zjnu.edu.cn

Funds: Project supported by the Key Program of the Natural Science Foundation of Zhejiang Province, China (Grant No. LZ21A040001) and the National Natural Science Foundation of China (Grant No. 12074344)

文章全文 : translate this paragraph

参考文献

[1]	Saito H, Ueda M 2003 Phys. Rev. Lett. 90 040403 Google Scholar
[2]	Zhang Y C, Zhou Z W, Malomed B A, Pu H 2015 Phys. Rev. Lett. 115 253901 Google Scholar
[3]	Dalfovo F, Stringari S 1996 Phys. Rev. A 53 2477 Google Scholar
[4]	Carr L D, Clark C W 2006 Phys. Rev. Lett. 97 010403 Google Scholar
[5]	Kartashov Y V, Malomed B A, Torner L 2011 Rev. Mod. Phys. 83 247 Google Scholar
[6]	Maucher F, Henkel N, Saffman M, Królikowski W, Skupin S, Pohl T 2011 Phys. Rev. Lett. 106 170401 Google Scholar
[7]	Tikhonenkov I, Malomed B A, Vardi A 2008 Phys. Rev. Lett. 100 090406 Google Scholar
[8]	Kippenberg T J, Gaeta A L, Lipson M, Gorodetsky M L 2018 Science 361 567 Google Scholar
[9]	Smirnov L A, Smirnova D A, Ostrovskaya E A, Kivshar Y S 2014 Phys. Rev. B 89 235310 Google Scholar
[10]	Xu X R, Chen L, Zhang Z D, Liang Z X 2019 J. Phys. B 52 025303 Google Scholar
[11]	Jia C Y, Liang Z X 2020 Chin. Phys. Lett. 37 040502 Google Scholar
[12]	Jia C Y, Wu R K, Hu Y, Liu W M, Liang Z X 2021 Front. Phys. 9 805841 Google Scholar
[13]	Zhang Y L, Jia C Y, Liang Z X 2022 Chin. Phys. Lett. 39 020501 Google Scholar
[14]	Jia C Y, Liang Z X 2022 Entropy 24 1789 Google Scholar
[15]	余超凡, 梁国栋, 曹锡金 2008 57 4402 Google Scholar Yu C F, Liang G D, Cao X J 2008 Acta Phys. Sin. 57 4402 Google Scholar
[16]	陈礼元, 高超, 林机, 李慧军 2022 71 181101 Google Scholar Chen L Y, Gao C, Lin J, Li H J 2022 Acta Phys. Sin. 71 181101 Google Scholar
[17]	Kasprzak J, Richard M, Kundermann S, et al. 2006 Nature 443 409 Google Scholar
[18]	Balili R, Hartwell V, Snoke D, Pfeiffer L, West K 2007 Science 316 1007 Google Scholar
[19]	Deng H, Weihs G, Santori C, Bloch J, Yamamoto Y 2002 Science 298 199 Google Scholar
[20]	Carusotto I, Ciuti C 2013 Rev. Mod. Phys. 85 299 Google Scholar
[21]	Byrnes T, Kim N Y, Yamamoto Y 2014 Nat. Phys. 10 803 Google Scholar
[22]	Plumhof J D, Stöferle T, Mai L, Scherf U, Mahrt R F 2014 Nat. Mater. 13 247 Google Scholar
[23]	Su R, Ghosh S, Wang J, Liu S, Diederichs C, Liew T C H, Xiong Q H 2020 Nat. Phys. 16 301 Google Scholar
[24]	李峰, 熊启华 2022 物理 51 445 Google Scholar Li F, Xiong Q H 2022 Physics 51 445 Google Scholar
[25]	Sieberer L M, Buchhold M, Diehl S 2016 Rep. Prog. Phys. 79 096001 Google Scholar
[26]	Ciuti C, Schwendimann P, Quattropani A 2001 Phys. Rev. B 63 041303(R Google Scholar
[27]	Klass M, Flayac H, Amthor M, Savenko I G, Brodbeck S, Ala-Nissila T, Klembt S, Schneider C, Höfling S 2018 Phys. Rev. Lett. 120 017401 Google Scholar
[28]	Schneider C, Winkler K, Fraser M D, Kamp M, Yamamoto Y, Ostrovskaya E A, Höfling S 2016 Rep. Prog. Phys. 80 016503 Google Scholar
[29]	Shelykh I A, Kavokin A V, Rubo Y G, Liew T C H, Malpuech G 2010 Semicond. Sci. Technol. 25 013001 Google Scholar
[30]	Sanvitto D, Kéna-Cohen S 2016 Nat. Mater. 15 1061 Google Scholar
[31]	Takemura N, Trebaol S, Wouters M, Portella-Oberli M T, Deveaud B 2014 Nat. Phys. 10 500 Google Scholar
[32]	Sun Y, Yoon Y, Steger M, Liu G, Pfeiffer L N, West K, Snoke D W, Nelson K A 2017 Nat. Phys. 13 870 Google Scholar
[33]	Navadeh-Toupchi M, Takemura N, Anderson M D, Oberli D Y, Portella-Oberli M T 2019 Phys. Rev. Lett. 122 047402 Google Scholar
[34]	Lai C W, Kim N Y, Utsunomiya S, et al. 2007 Nature 450 529 Google Scholar
[35]	St-Jean P, Goblot V, Galopin E, Lemaître A, Ozawa T, Le Gratiet T, Sagnes I, Bloch J, Amo A 2017 Nat. Photonics 11 651 Google Scholar
[36]	Manni F, Lagoudakis K G, Pietka B, Fontanesi L, Wouters M, Savona V, André R, Deveaud-Plédran B 2011 Phys. Rev. Lett. 106 176401 Google Scholar
[37]	Thunert M, Janot A, Franke H, Sturm C, Michalsky T, Martín T, Viña L, Rosenow B, Grundmann M, Schmidt-Grund R 2016 Phys. Rev. B 93 064203 Google Scholar
[38]	Sala V G, Solnyshkov D D, Carusotto I, et al. 2015 Phys. Rev. X 5 011034 Google Scholar
[39]	Whittaker C E, Cancellieri E, Walker P M, et al. 2018 Phys. Rev. Lett. 120 097401 Google Scholar
[40]	Klembt S, Harder T H, Egorov O A, et al. 2018 Nature 562 552 Google Scholar
[41]	Lim H T, Togan E, Kroner M, Miguel-Sanchez J, Imamoğlu A 2017 Nat. Commun. 8 14540 Google Scholar
[42]	陈海军, 任元, 王华 2022 71 056701 Google Scholar Chen H J, Ren Y, Wang H 2022 Acta Phys. Sin. 71 056701 Google Scholar
[43]	郭慧, 王雅君, 王林雪, 张晓斐 2020 69 010302 Google Scholar Guo H, Wang Y J, Wang L X, Zhang X F 2020 Acta Phys. Sin. 69 010302 Google Scholar
[44]	Kivshar Y S, Królikowski W 1995 Opt. Commun. 114 353 Google Scholar
[45]	Frantzeskakis D J 2010 J. Phys. A: Math. Theor. 43 213001 Google Scholar
[46]	Tran P 1998 Phys. Rev. E 58 8049 Google Scholar

施引文献

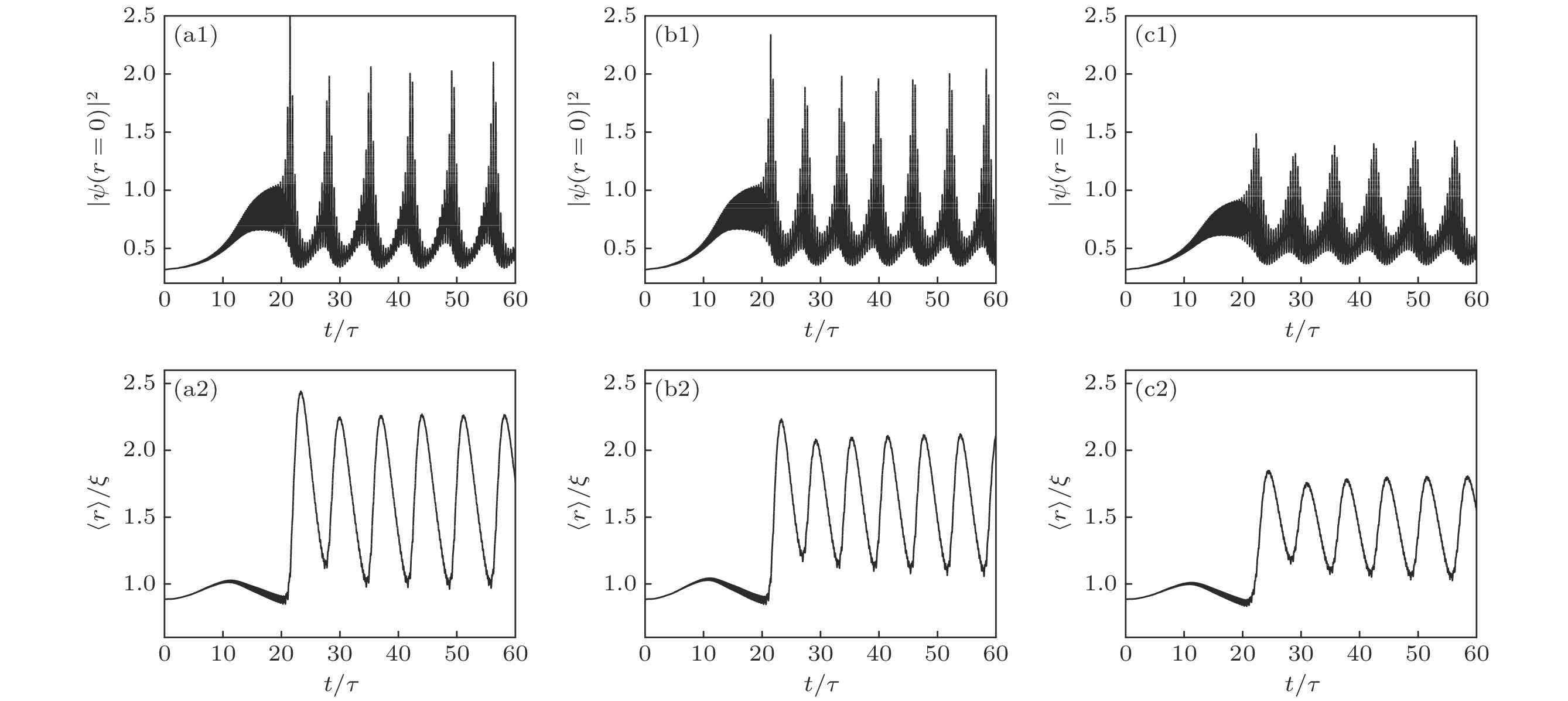
图 1 峰值密度$\left|\psi\left(r=0\right)\right|^{2}$和单极矩$\left\langle r\right\rangle = \displaystyle\int r\left|\psi\right|^{2}\mathrm{d}\boldsymbol{r}$随时间t演化的图像　(a1), (a2) $\gamma_{{\rm{C}}}=0.60$, $\gamma_{{\rm{R}}}=3.00$, $P_{0}=1.271$; (b1), (b2) $\gamma_{{\rm{C}}}=0.70$, $\gamma_{{\rm{R}}}=3.00$, $P_{0}=1.484$; (c1), (c2) $\gamma_{{\rm{C}}}=0.60$, $\gamma_{{\rm{R}}}=2.60$, $P_{0}=1.142$. 周期振荡相互作用强度取为$g(t)= $$ -2\pi+ 8\pi\sin(\varOmega t)$, 含时演化的前段$t=0$—20, 逐渐打开热源极化子间的相互作用, 同时缓慢减弱径向约束势到零. 其他参数为$R=2.40$, $\omega=2.00$, $\varOmega=30$, $g_{{\rm{R}}}=0$

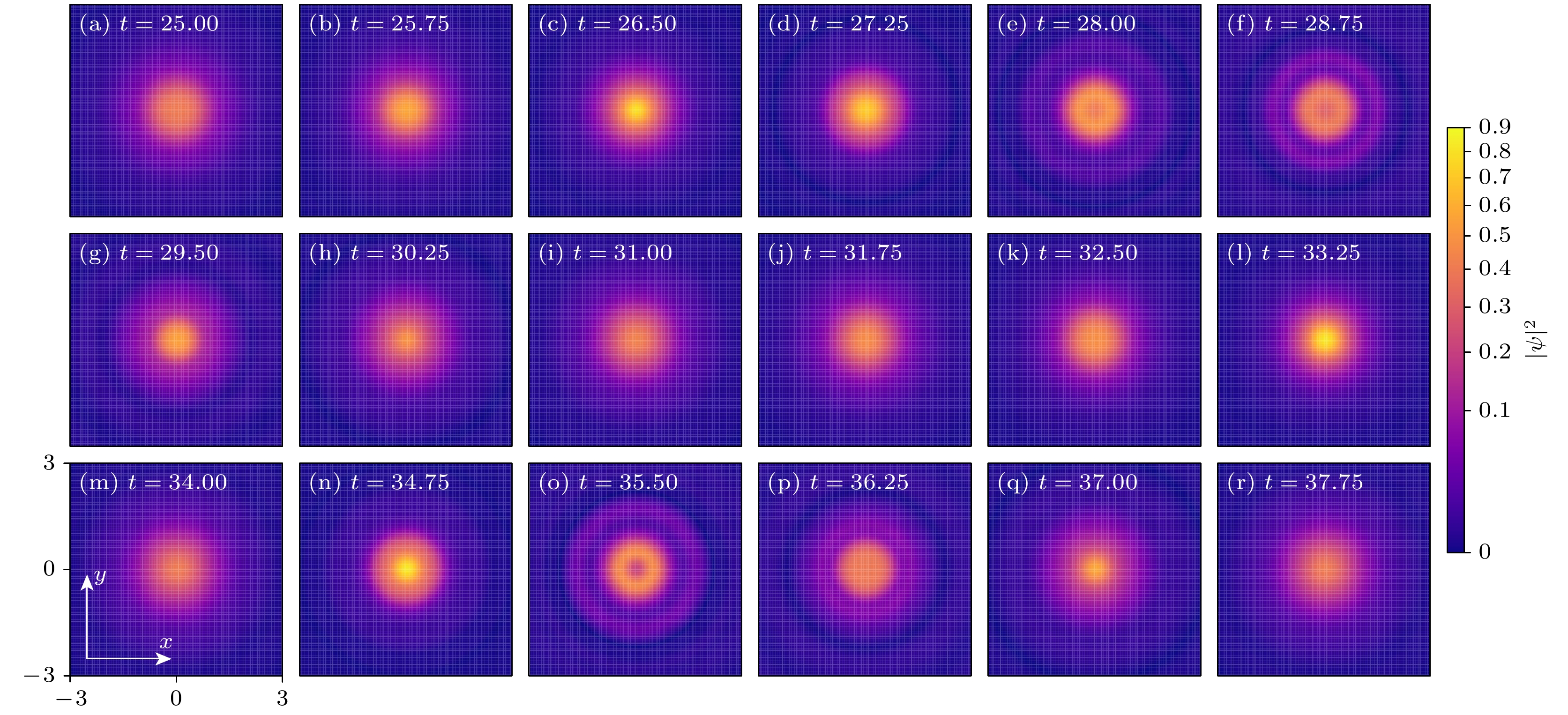
Fig. 1. Time evolution of the peak density $\left|\psi\left(r=0\right)\right|^{2}$ and the monopole moment $\left\langle r\right\rangle = \displaystyle\int r\left|\psi\right|^{2}\mathrm{d}\boldsymbol{r}$: (a1), (a2) $\gamma_{{\rm{C}}}=0.60$, $\gamma_{{\rm{R}}}=3.00$, $P_{0}=1.271$; (b1), (b2) $\gamma_{{\rm{C}}}=0.70$, $\gamma_{{\rm{R}}}=3.00$, $P_{0}=1.484$; (c1), (c2) $\gamma_{{\rm{C}}}=0.60$, $\gamma_{{\rm{R}}}=2.60$, $P_{0}=1.142$. The interaction $g(t)=-2\pi+8\pi\sin(\varOmega t)$ is switched on a little bit at a time while the radial confinement potential is switched off from $t=0$ to 20. Values of other parameters are $R=2.40$, $\omega=2.00$, $\varOmega=30$, $g_{{\rm{R}}}=0$

下载: 全尺寸图片幻灯片

图 2 图1(a)所描述系统中, 概率密度分布随时间演化的图像. 图中颜色明暗代表概率密度的大小, 颜色越亮表示对应的概率密度越大

Fig. 2. Time evolution of the the odds density distribution for the system depicted in Fig. 1(a). The brighter and darker colors in the figure represent the magnitude of the density, and the brighter color indicates the corresponding higher density

下载: 全尺寸图片幻灯片

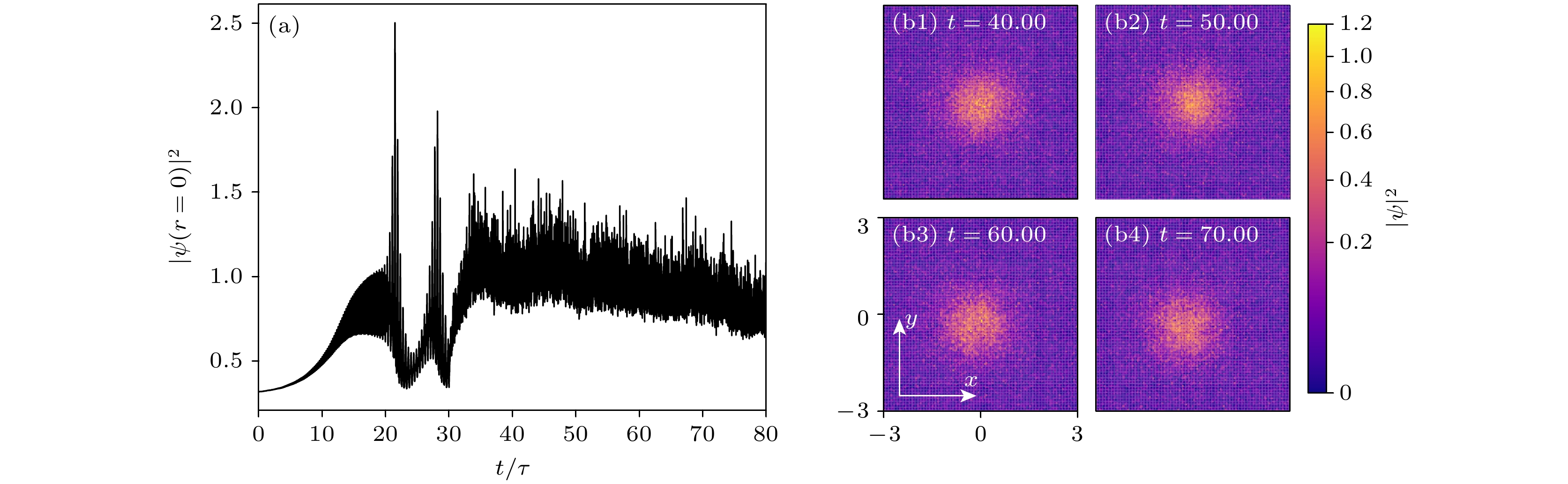
图 3 考虑噪声的快热库极限下, 峰值密度$\left|\psi\left(r=0\right)\right|^{2}$(a)随时间演化图像和(b)概率密度分布图像. 周期振荡相互作用强度取为$g(t)=-2\pi+8\pi\sin(\varOmega t)$, 噪音强度为$D=0.01$, 其他参数为$R=2.40$, $\gamma_{{\rm{C}}}=0.60$, $\gamma_{{\rm{R}}}=3.00$, $P_{0}=1.274$, $\omega=2.00$, $\varOmega=30$, $g_{{\rm{R}}}=0$. 图中颜色明暗代表概率密度的大小, 颜色越亮表示对应的概率密度越大

Fig. 3. (a) Time evolution of the peak density $\left|\psi\left(r=0\right)\right|^{2}$ and (b) the density distribution in the limit of fast reservoir considering the noise. The interaction $g(t)=-2\pi+8\pi\sin(\varOmega t)$ is switched on a little bit at a time while the radial confinement potential is switched off from $t=0$ to 20. The noise intensity is $D=0.01$. Values of other parameters are $R=2.40$, $\gamma_{{\rm{C}}}=0.60$, $\gamma_{{\rm{R}}}=3.00$, $P_{0}=1.274$, $\omega=2.00$, $\varOmega=30$, $g_{{\rm{R}}}=0$. The brighter and darker colors in the figure represent the magnitude of the density, and the brighter color indicates the corresponding higher density

下载: 全尺寸图片幻灯片

图 4 根据演化耦合方程(4)和方程(5), 峰值密度$\left|\psi\left(r=0\right)\right|^{2}$和概率密度分布图像　(a1)快热库参数空间中峰值密度$\left|\psi\left(r=0\right)\right|^{2}$随时间演化的图像, $R=2.40$, $\gamma_{{\rm{R}}}=3.00$; (b1)在图(a1)基础上再加入强度为$D=0.01$的弱噪声; (c1), (d1)考虑噪声的快热库参数空间中的概率密度分布图; (a2)非快热库参数空间中峰值密度$\left|\psi\left(r=0\right)\right|^{2}$随时间演化的图像, $R=0.24$, $\gamma_{{\rm{R}}}=0.30$; (b2)在图(a2)基础上再加入强度为$D=0.01$的弱噪声; (c2), (d2)考虑噪声的非快热库参数空间中的分叉率密度分布图. 周期振荡相互作用强度取为$g(t)=-2\pi+8\pi\sin(\varOmega t)$, 在$t=30$时加入高斯白噪声, 其他参数为$\gamma_{{\rm{C}}}=0.60$, $P_{0}=1.265$, $\omega=2.20$, $\varOmega=30$, $g_{{\rm{R}}}=0$. 图中颜色明暗代表概率密度的大小, 颜色越亮表示对应的概率密度越大

Fig. 4. Time evolution of the peak density $\left|\psi\left(r=0\right)\right|^{2}$ and the monopole moment $\left\langle r\right\rangle =\int r\left|\psi\right|^{2}\mathrm{d}\boldsymbol{r}$ while evolving the coupled equations (4) and (5): (a1) Image of peak density $\left|\psi\left(r=0\right)\right|^{2}$ in the parameter space of fast reservoir with time evolution, $R=2.40$, $\gamma_{{\rm{R}}}=3.00$; (b1) adding a weak noise with intensity D=0.01 to panel (a1); (c1), (d1) image of density distribution in the parameter space of fast reservoir considering the noise; (a2) image of peak density $\left|\psi\left(r=0\right)\right|^{2}$ in the parameter space of non-fast reservoir with time evolution, $R=0.24$, $\gamma_{{\rm{R}}}=0.30$; (b2) adding a weak noise with intensity D = 0.01 to panel (a2); (c2), (d2) image of density distribution in the parameter space of non-fast reservoir considering the noise. The interaction $g(t)=-2\pi+8\pi\sin(\varOmega t)$ is switched on a little bit at a time while the radial confinement potential is switched off from $t=0$ to 20. Gaussian white noise is added at the moment $t=30$, and the other parameters are $\gamma_{{\rm{C}}}=0.60$, $P_{0}=1.265$, $\omega=2.20$, $\varOmega=30$, $g_{{\rm{R}}}=0$. The brighter and darker colors in the figure represent the magnitude of the density, and the brighter color indicates the corresponding higher density

下载: 全尺寸图片幻灯片

map

[1]	Saito H, Ueda M 2003 Phys. Rev. Lett. 90 040403 Google Scholar
[2]	Zhang Y C, Zhou Z W, Malomed B A, Pu H 2015 Phys. Rev. Lett. 115 253901 Google Scholar
[3]	Dalfovo F, Stringari S 1996 Phys. Rev. A 53 2477 Google Scholar
[4]	Carr L D, Clark C W 2006 Phys. Rev. Lett. 97 010403 Google Scholar
[5]	Kartashov Y V, Malomed B A, Torner L 2011 Rev. Mod. Phys. 83 247 Google Scholar
[6]	Maucher F, Henkel N, Saffman M, Królikowski W, Skupin S, Pohl T 2011 Phys. Rev. Lett. 106 170401 Google Scholar
[7]	Tikhonenkov I, Malomed B A, Vardi A 2008 Phys. Rev. Lett. 100 090406 Google Scholar
[8]	Kippenberg T J, Gaeta A L, Lipson M, Gorodetsky M L 2018 Science 361 567 Google Scholar
[9]	Smirnov L A, Smirnova D A, Ostrovskaya E A, Kivshar Y S 2014 Phys. Rev. B 89 235310 Google Scholar
[10]	Xu X R, Chen L, Zhang Z D, Liang Z X 2019 J. Phys. B 52 025303 Google Scholar
[11]	Jia C Y, Liang Z X 2020 Chin. Phys. Lett. 37 040502 Google Scholar
[12]	Jia C Y, Wu R K, Hu Y, Liu W M, Liang Z X 2021 Front. Phys. 9 805841 Google Scholar
[13]	Zhang Y L, Jia C Y, Liang Z X 2022 Chin. Phys. Lett. 39 020501 Google Scholar
[14]	Jia C Y, Liang Z X 2022 Entropy 24 1789 Google Scholar
[15]	余超凡, 梁国栋, 曹锡金 2008 57 4402 Google Scholar Yu C F, Liang G D, Cao X J 2008 Acta Phys. Sin. 57 4402 Google Scholar
[16]	陈礼元, 高超, 林机, 李慧军 2022 71 181101 Google Scholar Chen L Y, Gao C, Lin J, Li H J 2022 Acta Phys. Sin. 71 181101 Google Scholar
[17]	Kasprzak J, Richard M, Kundermann S, et al. 2006 Nature 443 409 Google Scholar
[18]	Balili R, Hartwell V, Snoke D, Pfeiffer L, West K 2007 Science 316 1007 Google Scholar
[19]	Deng H, Weihs G, Santori C, Bloch J, Yamamoto Y 2002 Science 298 199 Google Scholar
[20]	Carusotto I, Ciuti C 2013 Rev. Mod. Phys. 85 299 Google Scholar
[21]	Byrnes T, Kim N Y, Yamamoto Y 2014 Nat. Phys. 10 803 Google Scholar
[22]	Plumhof J D, Stöferle T, Mai L, Scherf U, Mahrt R F 2014 Nat. Mater. 13 247 Google Scholar
[23]	Su R, Ghosh S, Wang J, Liu S, Diederichs C, Liew T C H, Xiong Q H 2020 Nat. Phys. 16 301 Google Scholar
[24]	李峰, 熊启华 2022 物理 51 445 Google Scholar Li F, Xiong Q H 2022 Physics 51 445 Google Scholar
[25]	Sieberer L M, Buchhold M, Diehl S 2016 Rep. Prog. Phys. 79 096001 Google Scholar
[26]	Ciuti C, Schwendimann P, Quattropani A 2001 Phys. Rev. B 63 041303(R Google Scholar
[27]	Klass M, Flayac H, Amthor M, Savenko I G, Brodbeck S, Ala-Nissila T, Klembt S, Schneider C, Höfling S 2018 Phys. Rev. Lett. 120 017401 Google Scholar
[28]	Schneider C, Winkler K, Fraser M D, Kamp M, Yamamoto Y, Ostrovskaya E A, Höfling S 2016 Rep. Prog. Phys. 80 016503 Google Scholar
[29]	Shelykh I A, Kavokin A V, Rubo Y G, Liew T C H, Malpuech G 2010 Semicond. Sci. Technol. 25 013001 Google Scholar
[30]	Sanvitto D, Kéna-Cohen S 2016 Nat. Mater. 15 1061 Google Scholar
[31]	Takemura N, Trebaol S, Wouters M, Portella-Oberli M T, Deveaud B 2014 Nat. Phys. 10 500 Google Scholar
[32]	Sun Y, Yoon Y, Steger M, Liu G, Pfeiffer L N, West K, Snoke D W, Nelson K A 2017 Nat. Phys. 13 870 Google Scholar
[33]	Navadeh-Toupchi M, Takemura N, Anderson M D, Oberli D Y, Portella-Oberli M T 2019 Phys. Rev. Lett. 122 047402 Google Scholar
[34]	Lai C W, Kim N Y, Utsunomiya S, et al. 2007 Nature 450 529 Google Scholar
[35]	St-Jean P, Goblot V, Galopin E, Lemaître A, Ozawa T, Le Gratiet T, Sagnes I, Bloch J, Amo A 2017 Nat. Photonics 11 651 Google Scholar
[36]	Manni F, Lagoudakis K G, Pietka B, Fontanesi L, Wouters M, Savona V, André R, Deveaud-Plédran B 2011 Phys. Rev. Lett. 106 176401 Google Scholar
[37]	Thunert M, Janot A, Franke H, Sturm C, Michalsky T, Martín T, Viña L, Rosenow B, Grundmann M, Schmidt-Grund R 2016 Phys. Rev. B 93 064203 Google Scholar
[38]	Sala V G, Solnyshkov D D, Carusotto I, et al. 2015 Phys. Rev. X 5 011034 Google Scholar
[39]	Whittaker C E, Cancellieri E, Walker P M, et al. 2018 Phys. Rev. Lett. 120 097401 Google Scholar
[40]	Klembt S, Harder T H, Egorov O A, et al. 2018 Nature 562 552 Google Scholar
[41]	Lim H T, Togan E, Kroner M, Miguel-Sanchez J, Imamoğlu A 2017 Nat. Commun. 8 14540 Google Scholar
[42]	陈海军, 任元, 王华 2022 71 056701 Google Scholar Chen H J, Ren Y, Wang H 2022 Acta Phys. Sin. 71 056701 Google Scholar
[43]	郭慧, 王雅君, 王林雪, 张晓斐 2020 69 010302 Google Scholar Guo H, Wang Y J, Wang L X, Zhang X F 2020 Acta Phys. Sin. 69 010302 Google Scholar
[44]	Kivshar Y S, Królikowski W 1995 Opt. Commun. 114 353 Google Scholar
[45]	Frantzeskakis D J 2010 J. Phys. A: Math. Theor. 43 213001 Google Scholar
[46]	Tran P 1998 Phys. Rev. E 58 8049 Google Scholar

[1]	杨佳奇, 刘文军. 基于变系数3+1维三次-五次复金兹堡-朗道方程的亮孤子及混合孤子传输特性. , 2023, 72(10): 100504. doi: 10.7498/aps.72.20222430
[2]	邱旭, 王林雪, 陈光平, 胡爱元, 文林. 自旋张量-动量耦合玻色-爱因斯坦凝聚的动力学性质. , 2023, 72(18): 180304. doi: 10.7498/aps.72.20231076
[3]	李新月, 祁娟娟, 赵敦, 刘伍明. 自旋-轨道耦合二分量玻色-爱因斯坦凝聚系统的孤子解. , 2023, 72(10): 106701. doi: 10.7498/aps.72.20222319
[4]	陈逸熙, 蔡晓妍, 刘彬, 江迅达, 黎永耀. 准二维空间中的隐秘涡旋量子液滴. , 2022, 71(20): 200302. doi: 10.7498/aps.71.20220709
[5]	吴昊, 任元, 刘通, 王元钦, 刑朝洋. 旋转二维激子极化激元凝聚涡旋叠加态的动力学特性. , 2020, 69(23): 230303. doi: 10.7498/aps.69.20200697
[6]	徐昕, 金雪莹, 高浩然, 程杰, 陆洋, 陈东, 于连栋. 耦合光学微腔的频率调谐过程分析. , 2020, 69(18): 184207. doi: 10.7498/aps.69.20200530
[7]	任金莲, 任恒飞, 陆伟刚, 蒋涛. 基于分裂格式有限点集法对孤立波二维非线性问题的模拟. , 2019, 68(14): 140203. doi: 10.7498/aps.68.20190340
[8]	文林, 梁毅, 周晶, 余鹏, 夏雷, 牛连斌, 张晓斐. 线性塞曼劈裂对自旋-轨道耦合玻色-爱因斯坦凝聚体中亮孤子动力学的影响. , 2019, 68(8): 080301. doi: 10.7498/aps.68.20182013
[9]	张解放, 戴朝卿. 非自治物质畸形波的传播操控. , 2016, 65(5): 050501. doi: 10.7498/aps.65.050501
[10]	党婷婷, 王娟芬, 安亚东, 刘香莲, 张朝霞, 杨玲珍. 亮孤子在宇称时间对称波导中的传输和控制. , 2015, 64(6): 064211. doi: 10.7498/aps.64.064211
[11]	徐园芬. 一维Tonks-Girardeau原子气区域中 Gross-Pitaevskii方程简化模型的精确行波解. , 2013, 62(10): 100202. doi: 10.7498/aps.62.100202
[12]	何章明, 王登龙, 丁建文, 颜晓红. 二元凝聚体中亮-亮孤子的振荡-局域转变行为. , 2012, 61(23): 230508. doi: 10.7498/aps.61.230508
[13]	宗丰德, 杨阳, 张解放. 外势场作用下的玻色-爱因斯坦凝聚啁啾孤子的演化与操控. , 2009, 58(6): 3670-3678. doi: 10.7498/aps.58.3670
[14]	宗丰德, 张解放. 装载于外势场中的玻色-爱因斯坦凝聚N-孤子间的相互作用. , 2008, 57(5): 2658-2668. doi: 10.7498/aps.57.2658
[15]	何章明, 王登龙. 凝聚体中亮孤子和暗孤子的交替演化. , 2007, 56(6): 3088-3091. doi: 10.7498/aps.56.3088
[16]	徐志君, 施建青, 李珍, 蔡萍根. 基于Gross-Pitaevskii能量泛函求解谐振势阱中玻色凝聚气体基态波函数. , 2006, 55(7): 3265-3271. doi: 10.7498/aps.55.3265
[17]	江德生, 佘卫龙. 多个光伏空间亮孤子相互作用研究. , 2005, 54(5): 2090-2095. doi: 10.7498/aps.54.2090
[18]	欧阳世根, 佘卫龙. 亮-暗复色光伏孤子. , 2004, 53(9): 3042-3048. doi: 10.7498/aps.53.3042
[19]	江德生, 欧阳世根, 佘卫龙. 暗-暗与亮-暗光伏孤子相互作用. , 2004, 53(11): 3777-3785. doi: 10.7498/aps.53.3777
[20]	李向正, 张金良, 王跃明, 王明亮. 非线性Schr?dinger方程的包络形式解. , 2004, 53(12): 4045-4051. doi: 10.7498/aps.53.4045

计量

文章访问数: 3135
PDF下载量: 124
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

激子极化激元凝聚体中的二维亮孤子