非规则形状介质内辐射-导热耦合传热的间断有限元求解

王存海; 郑树; 张欣欣

doi:10.7498/aps.69.20191185

摘要

采用间断有限元法(discontinuous finite element method, DFEM)求解非规则形状介质内的辐射导热耦合传热问题, 得到了典型非规则形状介质内辐射导热耦合传热问题的高精度数值结果. 和传统连续型有限元方法不同, DFEM将计算区域划分成相互独立的离散单元, 形函数的构造、未知量的加权近似以及控制方程的求解均在每一个离散单元上进行. 通过在单元之间施加迎风格式的数值通量, DFEM保证了整个计算区域的连续性, 因此这种方法兼具良好的几何灵活性和局部守恒性. 推导了辐射传输方程和能量扩散方程的DFEM离散格式, 验证了DFEM求解辐射导热耦合传热问题的正确性; 同时研究了不同几何形状介质内辐射导热耦合传热问题, 得到了典型非规则形状介质内辐射导热耦合传热的高精度数值结果.

关键词:

Abstract

The discontinuous finite element method (DFEM) is used to investigate the coupled radiation-conduction heat transfer in an irregular medium, and the highly accurate solutions for several typical media are numerically obtained. Comparing with the traditional continuous finite element method, the computational domain in the DFEM application is discretized into unstructured meshes that are assumed to be separated from each other. The shape function construction, field variable approximation, and numerical solutions are obtained for every single element. The continuity of the computational domain is maintained by modeling a numerical flux with the up-winding scheme. Thus the DFEM has the salient feature of geometry flexibility and simultaneously supports locally conservative solutions. The DFEM discretization for the radiative transfer equation and the energy diffusion equation are first presented, and the accuracies of the DFEM for coupled radiation-conduction heat transfer problems are verified. Combined radiation-conduction heat transfer problems in several irregular media are afterward solved, and the highly accurate DFEM solutions are presented.

Keywords:

作者及机构信息

1.
北京科技大学能源与环境工程学院, 北京　100083

2.
冶金工业节能减排北京市重点实验室, 北京　100083

3.
华北电力大学能源动力与机械工程学院, 北京　102206

通信作者: 王存海, wangcunhai@ustb.edu.cn ; 郑树, shuzheng@ncepu.edu.cn ;

基金项目: 国家自然科学基金(批准号: 51906014, 51890891)、中国博士后科学基金(批准号: 2018M641196)和中央高校基本科研业务费专项资金(批准号: FRF-TP-18-072A1)资助的课题

Authors and contacts

1.
School of Energy and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China

2.
Beijing Key Laboratory of Energy Conservation and Emission Reduction for Metallurgical Industry, Beijing 100083, China

3.
School of Energy, Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China

Corresponding author: Wang Cun-Hai, wangcunhai@ustb.edu.cn ; Zheng Shu, shuzheng@ncepu.edu.cn ;

Funds: the National Natural Science Foundation of China (Grant Nos. 51906014, 51890891), the China Postdoctoral Science Foundation (Grant No. 2018M641196), and the Fundamental Research Funds for the Central Universities (Grant No. FRF-TP-18-072A1)

文章全文 : translate this paragraph

参考文献

[1]	Viskanta R 1965 J. Heat Transf. 87 143 Google Scholar
[2]	Viskanta R, Incropera F P 1985 J. Sol. Energy Eng. 107 29 Google Scholar
[3]	Wang P Y, Tan H P, Liu L H, Tong T W 2000 J. Thermophys. Heat Transf. 14 512 Google Scholar
[4]	Zhang J Q, Nie L R, Chen C Y, Zhang X Y 2016 AIP Adv. 6 075212 Google Scholar
[5]	Chen R Y, Pan W L, Zhang J Q, Nie L R 2016 Chaos 26 093113 Google Scholar
[6]	Chen R Y, Tong L M, Nie L R, Wang C J, Pan W L 2017 Physica A 468 532 Google Scholar
[7]	李树, 李刚, 田东风, 邓力 2013 62 249501 Google Scholar Li S, Li G, Tian D F, Deng L 2013 Acta Phys. Sin. 62 249501 Google Scholar
[8]	Sun B, Wang H, Sun X B, Hong J, Zhang Y J 2012 Chin. Phys. B 21 129501 Google Scholar
[9]	Chen R Y, Nie L R, Chen C Y, Wang C J 2017 J. Stat. Mech.- Theory Exp. 013201 Google Scholar
[10]	Chen R Y, Nie L R, Chen C Y 2018 Chaos 28 053115 Google Scholar
[11]	梁子长, 金亚秋 2003 52 1319 Google Scholar Liang Z C, Jin Y Q 2003 Acta Phys. Sin. 52 1319 Google Scholar
[12]	Ben X, Yi H L, Tan H P 2014 Chin. Phys. B 23 099501 Google Scholar
[13]	赵军明 2007 博士学位论文 (哈尔滨: 哈尔滨工业大学) Zhao J M 2007 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[14]	赵军明, 刘林华 2007 化工学报 58 1110 Zhao J M, Liu L H 2007 J. Chem. Ind. Eng. 58 1110
[15]	胡帅, 高太长, 刘磊, 易红亮, 贲勋 2015 64 094201 Google Scholar Hu S, Gao T C, Liu L, Yi H L, Ben X 2015 Acta Phys. Sin. 64 094201 Google Scholar
[16]	Wang C H, Yi H L, Tan H P 2017 J. Quant. Spectrosc. Radiat. Transf. 189 383 Google Scholar
[17]	高效伟, 王静, 崔苗 2011 中国科学: 物理学力学天文学 41 302 Google Scholar Gao X W, Wang J, Cui M 2011 Sci. Sin. Phys. Mech. Astron. 41 302 Google Scholar
[18]	孙杰 2016 博士学位论文 (哈尔滨: 哈尔滨工业大学) Sun J 2016 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[19]	Wang C H, Feng Y Y, Yue K, Zhang X X 2019 Int. Commun. Heat Mass Transf. 108 104287 Google Scholar
[20]	Sun Y J, Zheng S Jiang B, Tang J C, Liu F S 2019 Int. J. Heat Mass Transf. 145 118777 Google Scholar
[21]	Tan J Y, Liu L H, Li B X 2006 Numer. Heat Transf. Part B-Fundam. 49 179 Google Scholar
[22]	Wang C H, Qu L, Zhang Y, Yi H L 2018 J. Quant. Spectrosc. Radiat. Transf. 208 108 Google Scholar
[23]	Liu L H, Tan J Y, Li B X 2006 J. Quant. Spectrosc. Radiat. Transf. 101 237 Google Scholar
[24]	Wang C H, Feng Y Y, Ben X, Yue K, Zhang X X 2019 Opt. Express 27 A981 Google Scholar
[25]	Sun S C, Wang G J, Chen H, Zhang D Q 2019 Int. J. Heat Mass Transf. 134 574 Google Scholar
[26]	Zheng S, Yang Y, Zhou H 2019 Int. J. Heat Mass Transf. 129 1232 Google Scholar
[27]	张克瑾, 刘磊, 曾庆伟, 高太长, 胡帅, 陈鸣 2019 68 194207 Google Scholar Zhang K J, Liu L, Zeng Q W, Gao T C, Hu S, Chen M 2019 Acta Phys. Sin. 68 194207 Google Scholar
[28]	Mishra S C, Krishna C H, Kim M Y 2011 Numer. Heat Transf. Part A-Appl. 60 254 Google Scholar
[29]	Mishra S C, Roy H K 2007 J. Comput. Phys. 223 89 Google Scholar
[30]	Howell J R, Menguc M P 2018 J. Quant. Spectrosc. Radiat. Transf. 221 253 Google Scholar
[31]	Zabihi M, Lari K, Amiri H 2017 J. Braz. Soc. Mech. Sci. Eng. 39 2847 Google Scholar
[32]	Hesthaven J S, Warburton T 2007 Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications (New York: Springer Science & Business Media)
[33]	Cui X, Li B Q 2005 J. Quant. Spectrosc. Radiat. Transf. 96 383 Google Scholar
[34]	Liu L H, Liu L J 2007 J. Quant. Spectrosc. Radiat. Transf. 105 377 Google Scholar
[35]	王存海, 易红亮, 谈和平 2017 工程热 38 833 Wang C H, Yi H L, Tan H P 2017 J. Eng. Thermophys. 38 833
[36]	Wang C H, Yi H L, Tan H P 2017 Appl. Opt. 56 1861 Google Scholar
[37]	Wang C H, Yi H L, Tan H P 2017 Opt. Express 25 14621 Google Scholar
[38]	Feng Y Y, Wang C H 2018 Int. J. Heat Mass Transf. 126 783 Google Scholar
[39]	Mishra S C, Talukdar P, Trimis D, Durst F 2003 Int. J. Heat Mass Transf. 46 3083 Google Scholar
[40]	Sun Y, Zhang X 2018 Int. J. Heat Mass Transf. 121 1039 Google Scholar

施引文献

图 1 (a)空间网格; (b)相邻单元间数值通量示意图

Fig. 1. (a) Spatial mesh; (b) sketch of numerical flux across the adjacent elements.

下载: 全尺寸图片幻灯片

图 2 方形介质对称线x/L = 0.5上无量纲温度T/T_b分布　(a)不同空间网格划分; (b)不同角度划分

Fig. 2. Dimensionless temperature T/T_b along the symmetry line x/L = 0.5 for the cases: (a) Different spatial discretization schemes; (b) different angular discretization schemes.

下载: 全尺寸图片幻灯片

图 3 方形介质对称线x/L = 0.5上无量纲温度的DFEM结果和DTM结果对比　(a)不同普朗克数; (b)不同散射反照率

Fig. 3. Comparison of dimensionless temperature along the square medium symmetry line x/L = 0.5 obtained by DFEM and DTM for the cases: (a) Different Planck numbers; (b) different scattering albedos.

下载: 全尺寸图片幻灯片

图 4 不同数值方法得到的方形介质对称线上的无量纲温度对比

Fig. 4. Comparison of dimensionless temperature along the square medium symmetry line x/L = 0.5 obtained by different numerical methods.

下载: 全尺寸图片幻灯片

图 5 内含圆形热壁面的半圆形介质　(a)结构示意图; (b)网格划分

Fig. 5. Semicircle medium with an inner circle hot boundary: (a) Geometry sketch; (b) spatial discretization.

下载: 全尺寸图片幻灯片

图 6 不同数值方法得到的半圆介质对称线上温度分布　(a) y = [0.0, 0.2]; (b) y = [0.6, 1.0]

Fig. 6. Temperature distributions along the symmetric line of the semicircle medium obtained by different numerical algorithms: (a) y = [0.0, 0.2]; (b) y = [0.6, 1.0].

下载: 全尺寸图片幻灯片

图 7 不同普朗克数条件下半圆介质底边上总热流密度分布　(a) N_pl = 0.1, (b) N_pl = 1.0

Fig. 7. Total flux distributions along the bottom boundary of the semicircle medium under the situations with different Plank numbers: (a) N_pl = 0.1; (b) N_pl = 1.0.

下载: 全尺寸图片幻灯片

图 8 内含圆形热边界的非规则形状介质　(a)结构示意图; (b)网格划分

Fig. 8. Irregular medium with an inner hot boundary: (a) Geometry sketch; (b) spatial discretization.

下载: 全尺寸图片幻灯片

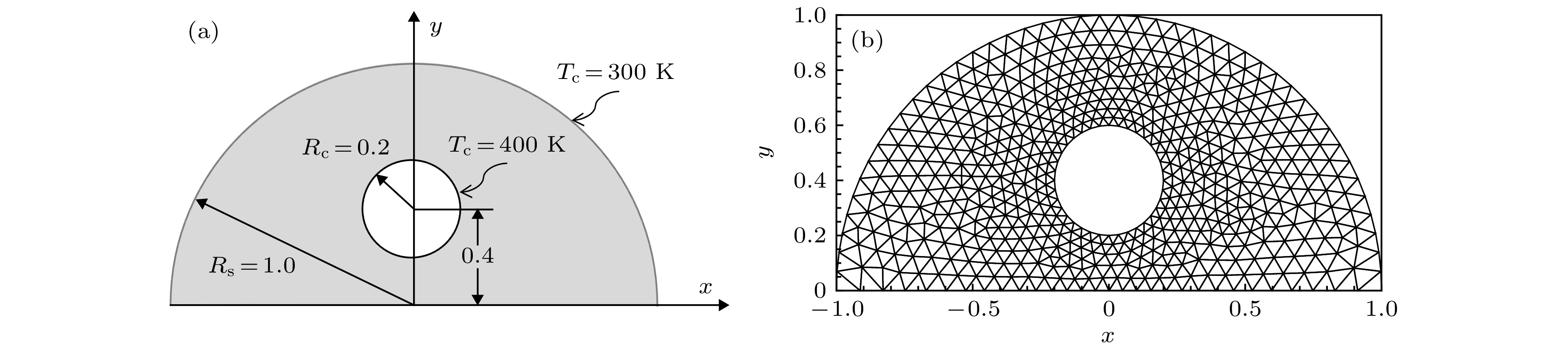
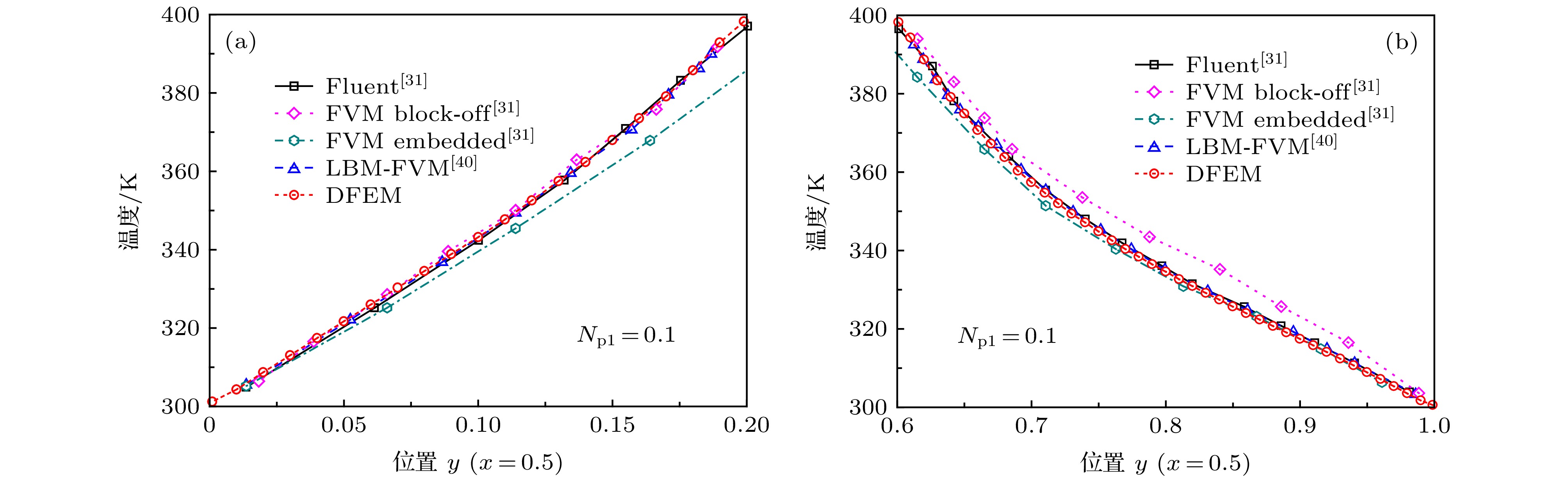
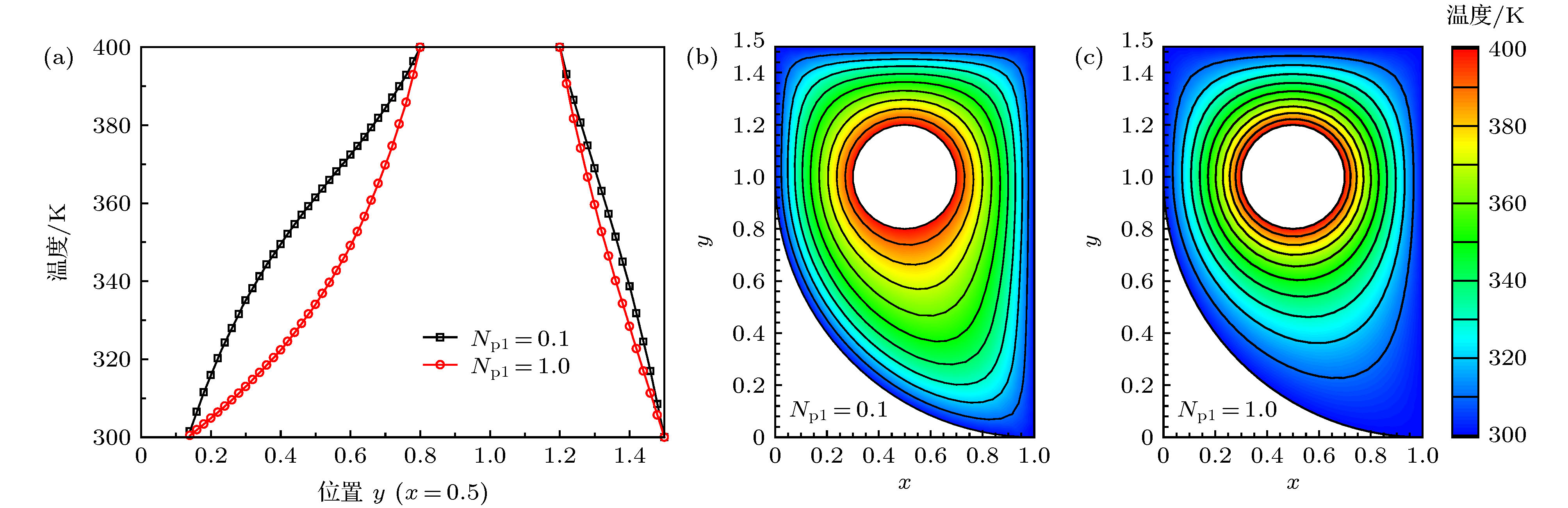
图 9 (a)普朗克数N_pl = 0.1和1.0时内含圆形热边界的非规则形状介质中线上温度分布; (b) N_pl = 0.1时介质温度分布; (c) N_pl = 1.0时介质温度分布

Fig. 9. (a) Temperature distributions along the centerline of the irregular medium with an inner hot boundary; (b) temperature distribution within the computation domain for the case of N_pl = 0.1; (c) temperature distribution within the computation domain for the case of N_pl = 1.0.

下载: 全尺寸图片幻灯片

图 10 内含两个圆形热边界的矩形介质　(a)结构示意图; (b)网格划分

Fig. 10. The medium the square medium with two circular hot boundaries: (a) Geometry sketch; (b) spatial discr etization.

下载: 全尺寸图片幻灯片

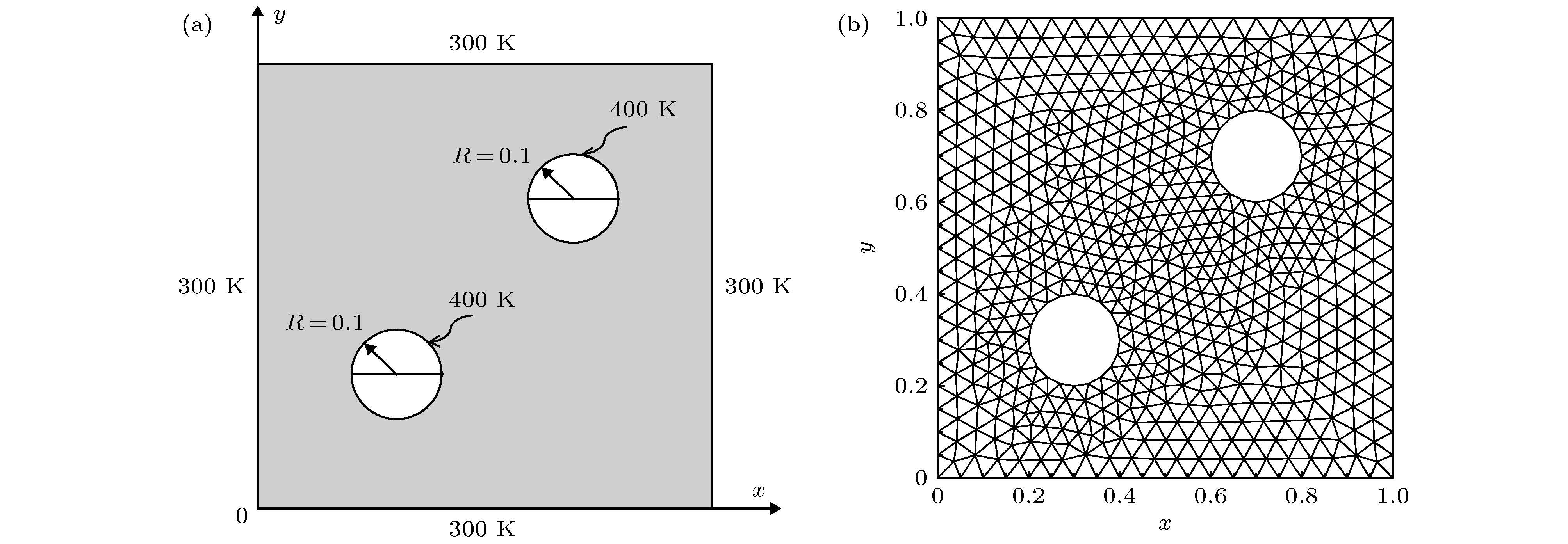
图 11 (a)普朗克数N_pl = 0.1和1.0时内含两个圆形热边界的矩形介质中线上温度分布; (b) N_pl = 0.1时介质温度分布; (c) N_pl = 1.0时介质温度分布

Fig. 11. (a) Temperature distributions along the centerline of the square medium with two circular hot boundaries; (b) temperature distribution within the computation domain for the case of N_pl = 0.1; (c) temperature distribution within the computation domain for the case of N_pl = 1.0

下载: 全尺寸图片幻灯片

map

[1]	Viskanta R 1965 J. Heat Transf. 87 143 Google Scholar
[2]	Viskanta R, Incropera F P 1985 J. Sol. Energy Eng. 107 29 Google Scholar
[3]	Wang P Y, Tan H P, Liu L H, Tong T W 2000 J. Thermophys. Heat Transf. 14 512 Google Scholar
[4]	Zhang J Q, Nie L R, Chen C Y, Zhang X Y 2016 AIP Adv. 6 075212 Google Scholar
[5]	Chen R Y, Pan W L, Zhang J Q, Nie L R 2016 Chaos 26 093113 Google Scholar
[6]	Chen R Y, Tong L M, Nie L R, Wang C J, Pan W L 2017 Physica A 468 532 Google Scholar
[7]	李树, 李刚, 田东风, 邓力 2013 62 249501 Google Scholar Li S, Li G, Tian D F, Deng L 2013 Acta Phys. Sin. 62 249501 Google Scholar
[8]	Sun B, Wang H, Sun X B, Hong J, Zhang Y J 2012 Chin. Phys. B 21 129501 Google Scholar
[9]	Chen R Y, Nie L R, Chen C Y, Wang C J 2017 J. Stat. Mech.- Theory Exp. 013201 Google Scholar
[10]	Chen R Y, Nie L R, Chen C Y 2018 Chaos 28 053115 Google Scholar
[11]	梁子长, 金亚秋 2003 52 1319 Google Scholar Liang Z C, Jin Y Q 2003 Acta Phys. Sin. 52 1319 Google Scholar
[12]	Ben X, Yi H L, Tan H P 2014 Chin. Phys. B 23 099501 Google Scholar
[13]	赵军明 2007 博士学位论文 (哈尔滨: 哈尔滨工业大学) Zhao J M 2007 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[14]	赵军明, 刘林华 2007 化工学报 58 1110 Zhao J M, Liu L H 2007 J. Chem. Ind. Eng. 58 1110
[15]	胡帅, 高太长, 刘磊, 易红亮, 贲勋 2015 64 094201 Google Scholar Hu S, Gao T C, Liu L, Yi H L, Ben X 2015 Acta Phys. Sin. 64 094201 Google Scholar
[16]	Wang C H, Yi H L, Tan H P 2017 J. Quant. Spectrosc. Radiat. Transf. 189 383 Google Scholar
[17]	高效伟, 王静, 崔苗 2011 中国科学: 物理学力学天文学 41 302 Google Scholar Gao X W, Wang J, Cui M 2011 Sci. Sin. Phys. Mech. Astron. 41 302 Google Scholar
[18]	孙杰 2016 博士学位论文 (哈尔滨: 哈尔滨工业大学) Sun J 2016 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[19]	Wang C H, Feng Y Y, Yue K, Zhang X X 2019 Int. Commun. Heat Mass Transf. 108 104287 Google Scholar
[20]	Sun Y J, Zheng S Jiang B, Tang J C, Liu F S 2019 Int. J. Heat Mass Transf. 145 118777 Google Scholar
[21]	Tan J Y, Liu L H, Li B X 2006 Numer. Heat Transf. Part B-Fundam. 49 179 Google Scholar
[22]	Wang C H, Qu L, Zhang Y, Yi H L 2018 J. Quant. Spectrosc. Radiat. Transf. 208 108 Google Scholar
[23]	Liu L H, Tan J Y, Li B X 2006 J. Quant. Spectrosc. Radiat. Transf. 101 237 Google Scholar
[24]	Wang C H, Feng Y Y, Ben X, Yue K, Zhang X X 2019 Opt. Express 27 A981 Google Scholar
[25]	Sun S C, Wang G J, Chen H, Zhang D Q 2019 Int. J. Heat Mass Transf. 134 574 Google Scholar
[26]	Zheng S, Yang Y, Zhou H 2019 Int. J. Heat Mass Transf. 129 1232 Google Scholar
[27]	张克瑾, 刘磊, 曾庆伟, 高太长, 胡帅, 陈鸣 2019 68 194207 Google Scholar Zhang K J, Liu L, Zeng Q W, Gao T C, Hu S, Chen M 2019 Acta Phys. Sin. 68 194207 Google Scholar
[28]	Mishra S C, Krishna C H, Kim M Y 2011 Numer. Heat Transf. Part A-Appl. 60 254 Google Scholar
[29]	Mishra S C, Roy H K 2007 J. Comput. Phys. 223 89 Google Scholar
[30]	Howell J R, Menguc M P 2018 J. Quant. Spectrosc. Radiat. Transf. 221 253 Google Scholar
[31]	Zabihi M, Lari K, Amiri H 2017 J. Braz. Soc. Mech. Sci. Eng. 39 2847 Google Scholar
[32]	Hesthaven J S, Warburton T 2007 Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications (New York: Springer Science & Business Media)
[33]	Cui X, Li B Q 2005 J. Quant. Spectrosc. Radiat. Transf. 96 383 Google Scholar
[34]	Liu L H, Liu L J 2007 J. Quant. Spectrosc. Radiat. Transf. 105 377 Google Scholar
[35]	王存海, 易红亮, 谈和平 2017 工程热 38 833 Wang C H, Yi H L, Tan H P 2017 J. Eng. Thermophys. 38 833
[36]	Wang C H, Yi H L, Tan H P 2017 Appl. Opt. 56 1861 Google Scholar
[37]	Wang C H, Yi H L, Tan H P 2017 Opt. Express 25 14621 Google Scholar
[38]	Feng Y Y, Wang C H 2018 Int. J. Heat Mass Transf. 126 783 Google Scholar
[39]	Mishra S C, Talukdar P, Trimis D, Durst F 2003 Int. J. Heat Mass Transf. 46 3083 Google Scholar
[40]	Sun Y, Zhang X 2018 Int. J. Heat Mass Transf. 121 1039 Google Scholar

[1]	于博文, 何孝天, 徐进良. 超临界CO₂池式传热流固耦合传热特性数值模拟. , 2024, 73(10): 104401. doi: 10.7498/aps.73.20231953
[2]	牛越, 包为民, 李小平, 刘彦明, 刘东林. 大功率热平衡感应耦合等离子体数值模拟及实验研究. , 2021, 70(9): 095204. doi: 10.7498/aps.70.20201610
[3]	庄晓如, 徐心海, 杨智, 赵延兴, 余鹏. 高温吸热管内超临界CO₂传热特性的数值模拟. , 2021, 70(3): 034401. doi: 10.7498/aps.70.20201005
[4]	林茜, 谢普初, 胡建波, 张凤国, 王裴, 王永刚. 不同晶粒度高纯铜层裂损伤演化的有限元模拟. , 2021, 70(20): 204601. doi: 10.7498/aps.70.20210726
[5]	闫晨帅, 徐进良. 超临界压力CO₂在水平圆管内流动传热数值分析. , 2020, 69(4): 044401. doi: 10.7498/aps.69.20191513
[6]	喻明浩. 非平衡感应耦合等离子体流场与电磁场作用机理的数值模拟. , 2019, 68(18): 185202. doi: 10.7498/aps.68.20190865
[7]	张忠宇, 姚熊亮, 张阿漫. 基于间断有限元方法的并列圆柱层流流动特性. , 2016, 65(8): 084701. doi: 10.7498/aps.65.084701
[8]	高新强, 沈俊, 和晓楠, 唐成春, 戴巍, 李珂, 公茂琼, 吴剑峰. 耦合高压斯特林制冷效应的复合磁制冷循环的数值模拟. , 2015, 64(21): 210201. doi: 10.7498/aps.64.210201
[9]	王平, 尹玉真, 沈胜强. 三维有序排列多孔介质对流换热的数值研究. , 2014, 63(21): 214401. doi: 10.7498/aps.63.214401
[10]	高启, 张传飞, 周林, 李正宏, 吴泽清, 雷雨, 章春来, 祖小涛. Z箍缩Al等离子体X特征辐射谱线数值模拟及考虑叠加效应后的修正. , 2014, 63(12): 125202. doi: 10.7498/aps.63.125202
[11]	殷鹏飞, 张蓉, 熊江涛, 李京龙. 搅拌摩擦焊准稳态热力耦合过程数值模拟研究. , 2013, 62(1): 018102. doi: 10.7498/aps.62.018102
[12]	王新鑫, 樊丁, 黄健康, 黄勇. 双钨极耦合电弧数值模拟. , 2013, 62(22): 228101. doi: 10.7498/aps.62.228101
[13]	刘磊, 费建芳, 黄小刚, 程小平. 大气-海浪-海流耦合模式的建立和一次台风过程的初步试验. , 2012, 61(14): 149201. doi: 10.7498/aps.61.149201
[14]	白占国, 董丽芳, 李永辉, 范伟丽. 双层耦合Lengel-Epstein模型中的超点阵斑图. , 2011, 60(11): 118201. doi: 10.7498/aps.60.118201
[15]	王蓬, 田修波, 汪志健, 巩春志, 杨士勤. 有限尺寸方靶等离子体离子注入动力学的三维粒子模拟研究. , 2011, 60(8): 085206. doi: 10.7498/aps.60.085206
[16]	赵啦啦, 刘初升, 闫俊霞, 徐志鹏. 颗粒分层过程三维离散元法模拟研究. , 2010, 59(3): 1870-1876. doi: 10.7498/aps.59.1870
[17]	胡玥, 饶海波. 单层有机器件的电子传输特性的数值模拟. , 2009, 58(5): 3474-3478. doi: 10.7498/aps.58.3474
[18]	胡玥, 饶海波, 李君飞. ITO/有机半导体/金属结构OLED器件的数值模拟. , 2008, 57(9): 5928-5932. doi: 10.7498/aps.57.5928
[19]	朱昌盛, 王智平, 荆涛, 肖荣振. 二元合金微观偏析的相场法数值模拟. , 2006, 55(3): 1502-1507. doi: 10.7498/aps.55.1502
[20]	张旭, 沈柯. 时空混沌的单向耦合同步. , 2002, 51(12): 2702-2706. doi: 10.7498/aps.51.2702

计量

文章访问数: 8341
PDF下载量: 115
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

非规则形状介质内辐射-导热耦合传热的间断有限元求解