-
混合型量子点系统是研究热电转换机制的良好平台. 本文提出了一个含自旋-轨道作用的双量子点耦合金属和超导体构成的混合型系统模型, 并对其电荷以及自旋热电输运特征进行研究. 深入讨论了热电系数与系统参数之间的关系, 结果发现系统存在显著的维德曼-弗兰兹定律违背现象, 这有助于增强热电转换效率. 更重要的是, 由于存在超导体能隙外的准粒子隧穿, 这个混合型热电器件能够产生纯自旋塞贝克效应. 在实践上, 该效应可以被利用设计和制造一个纯自旋流发生器. 在线性响应机制下, 本文也讨论了该混合型热电系统作为一个热机的热力学性能. 本研究结果对于理解混合型热电系统的热电转换特征及其热力学性能具有理论和实践意义.The normal metal-quantum dots-superconductor hybrid system is a good platform for studying the mechanism of thermoelectric conversion. In terms of non-equilibrium Keldysh Green’s function formalism and linear response theory, the charge and spin thermoelectric transport characteristics of a normal-double quantum dot-superconductor hybrid system with spin-orbit coupling are studied in this work. We delve into the relationship between thermoelectric coefficients and the system parameters, and find both charge and spin thermoelectric coefficients exhibit distinct symmetry in the parameter space composed of temperature and energy. The increase in temperature leads to a decrease in conductance within the energy gap, which is attributed to the reduction in Andreev transport. However, outside the energy gap, the conductance gradually increases, and the thermal conductance is gradually enhanced. This is because more quasiparticles outside the energy gap participate in thermoelectric transport, and a large charge thermopower is generated in the region far from the energy gap. It is found that the thermoelectric figure of merit is greater than 1, indicating a strong violation of the Wiedemann-Franz law. With the increase of temperature, the large spin thermopower as well as spin thermoelectric figure of merit can be obtained outside the energy gap. The charge (spin) thermopower and the thermoelectric figure of merit show the rich evolutionary characteristics as functions of energy level and Zeeman energy. With the disappearance of the charge thermopower, the spin thermopower still has a finite value, which leads to the emergence of a pure spin Seebeck effect. This is helpful for designing a pure spin current thermoelectric generator. Due to a competitive mechanism between the spin-orbit coupling effect and the Zeeman field, thermoelectric coefficients decrease with the strength of spin-orbit interaction increasing, but one still can obtain the spin thermoelectric quantities which meet the practical needs by regulating the strength of spin-orbit coupling and the Zeeman energy. The evolution pattern of the thermoelectric coefficientss in the energy space indicates that the enhancement of thermoelectric conversion efficiency can be achieved by modulating the energy levels of double quantum dots. In addition, this hybrid system can act as a heat engine to achieve the conversion of heat into work. Although its power and efficiency do not evolve synchronously, thermodynamic performance that meets practical needs can still be obtained in certain parameter regions. The research results of this work hold theoretical and practical significance for understanding the thermoelectric transport and thermodynamic performance of hybrid thermoelectric systems.
-
Keywords:
- hybrid quantum dot system /
- spin-orbit coupling /
- thermoelectric transport /
- power and efficiency
[1] 陈晓彬, 段文晖 2015 64 186302
 Google Scholar
Google Scholar
Chen X B, Duan W H 2015 Acta Phys. Sin. 64 186302
 Google Scholar
Google Scholar
[2] Mahan G D, Sofo J O 1996 Proc. Natl. Acad. Sci. USA 93 7436
 Google Scholar
Google Scholar
[3] Liu J, Sun Q F, Xie X C 2010 Phys. Rev. B 81 245323
 Google Scholar
Google Scholar
[4] Swirkowicz R, Wierzbicki M, Barnas J 2009 Phys. Rev. B 80 195409
 Google Scholar
Google Scholar
[5] Mazal Y, Meir Y, Dubi Y 2019 Phys. Rev. B 99 075433
 Google Scholar
Google Scholar
[6] Chida K, Fujiwara A, Nishiguchi K 2022 Appl. Phys. Lett. 121 183501
 Google Scholar
Google Scholar
[7] Sanduleac I, Pflaum J, Casian A 2019 J. Appl. Phys. 126 175501
 Google Scholar
Google Scholar
[8] Gomes T C S C, Marchal N, Araujo F A, Piraux L 2019 Appl. Phys. Lett. 115 242402
 Google Scholar
Google Scholar
[9] Wierzbicki M, Swirkowicz R 2010 J. Phys.: Condens. Matter 22 185302
 Google Scholar
Google Scholar
[10] Wang R Q, Shen L, Shen R, Wang B G, Xing D Y 2010 Phys. Rev. Lett. 105 057202
 Google Scholar
Google Scholar
[11] Bao W S, Liu Y S, Lei X L 2010 J. Phys.: Condens. Matter 22 315502
 Google Scholar
Google Scholar
[12] Ghawri B, Mahapatra P S, Garg M, Mandal S, Jayaraman A, Watanabe K, Taniguchi T, Jain M, Chandni U, Ghosh A 2024 Phys. Rev. B 109 045436
 Google Scholar
Google Scholar
[13] Anderson L E, Laitinen A, Zimmerman A, Werkmeister T, Shackleton H, Kruchkov A, Taniguchi T, Watanabe K, Sachdev S, Kim P 2024 Phys. Rev. Lett. 132 246502
 Google Scholar
Google Scholar
[14] Li J, Niquet Y M, Delerue C 2023 Phys. Rev. B 107 245417
 Google Scholar
Google Scholar
[15] Xu Y, Gan Z X, Zhang S C 2014 Phys. Rev. Lett. 112 226801
 Google Scholar
Google Scholar
[16] Blasi G, Taddei F, Arrachea L, Carrega M, Braggio A 2020 Phys. Rev. Lett. 124 227701
 Google Scholar
Google Scholar
[17] Sebastian Bergeret F, Silaev M, Virtanen P, Heikkilä T T 2018 Rev. Mod. Phys. 90 041001
 Google Scholar
Google Scholar
[18] Hwang S Y, Lopez R, Sanchez D 2016 Phys. Rev. B 94 054506
 Google Scholar
Google Scholar
[19] Hwang S Y, Sanchez D, Lopez R 2016 New. J. Phys. 18 093024
 Google Scholar
Google Scholar
[20] Trocha P, Barnas J 2017 Phys. Rev. B 95 165439
 Google Scholar
Google Scholar
[21] Michaek G, Urbaniak M, Bulka B R, Domanski T, Wysokinski K I 2016 Phys. Rev. B 93 235440
 Google Scholar
Google Scholar
[22] Dutta P, Alves K R, Black-Schaffer A M 2020 Phys. Rev. B 102 094513
 Google Scholar
Google Scholar
[23] Linder J, Balatsky A V 2019 Rev. Mod. Phys. 91 045005
 Google Scholar
Google Scholar
[24] Kubala B, Konig J 2002 Phys. Rev. B 65 245301
 Google Scholar
Google Scholar
[25] Chi F, Li S S 2006 J. Appl. Phys. 100 113703
 Google Scholar
Google Scholar
[26] Kang K, Cho S Y 2004 J. Phys.: Condens. Matter 16 117
 Google Scholar
Google Scholar
[27] Lu H Z, Lü R, Zhu B F 2005 Phys. Rev. B 71 235320
 Google Scholar
Google Scholar
[28] Kubo T, Tokura Y, Tarucha S 2011 Phys. Rev. B 83 115310
 Google Scholar
Google Scholar
[29] Pan H, Lin T H 2006 Phys. Rev. B 74 235312
 Google Scholar
Google Scholar
[30] Bordoloi A, Zannier V, Sorba L, Schrnenberger C, Baumgartner A 2020 Commun. Phys. 3 135
 Google Scholar
Google Scholar
[31] Bittermann L, Dominguez F, Recher P 2024 Phys. Rev. B 110 045429
 Google Scholar
Google Scholar
[32] Bułka B R 2022 Phys. Rev. B 106 085424
 Google Scholar
Google Scholar
[33] Yao H, Zhang C, Li Z J, Nie Y H, Niu P B 2018 J. Phys. D: Appl. Phys. 51 175301
 Google Scholar
Google Scholar
[34] Bai L, Zhang L, Tang F R, Zhang R 2023 J. Appl. Phys. 134 184304
 Google Scholar
Google Scholar
[35] Hussein R, Governale M, Sigmund Kohler S, Belzig W, Giazotto F, Alessandro Braggio A 2019 Phys. Rev. B 99 075429
 Google Scholar
Google Scholar
[36] Tabatabaei S M, Sánchez D, Yeyati A L, Sánchez R 2022 Phys. Rev. B 106 115419
 Google Scholar
Google Scholar
[37] Sánchez R, Burset P, Yeyati A L 2018 Phys. Rev. B 98 241414
 Google Scholar
Google Scholar
[38] Gresta D, Real M, Arrachea L 2019 Phys. Rev. Lett. 123 186801
 Google Scholar
Google Scholar
-
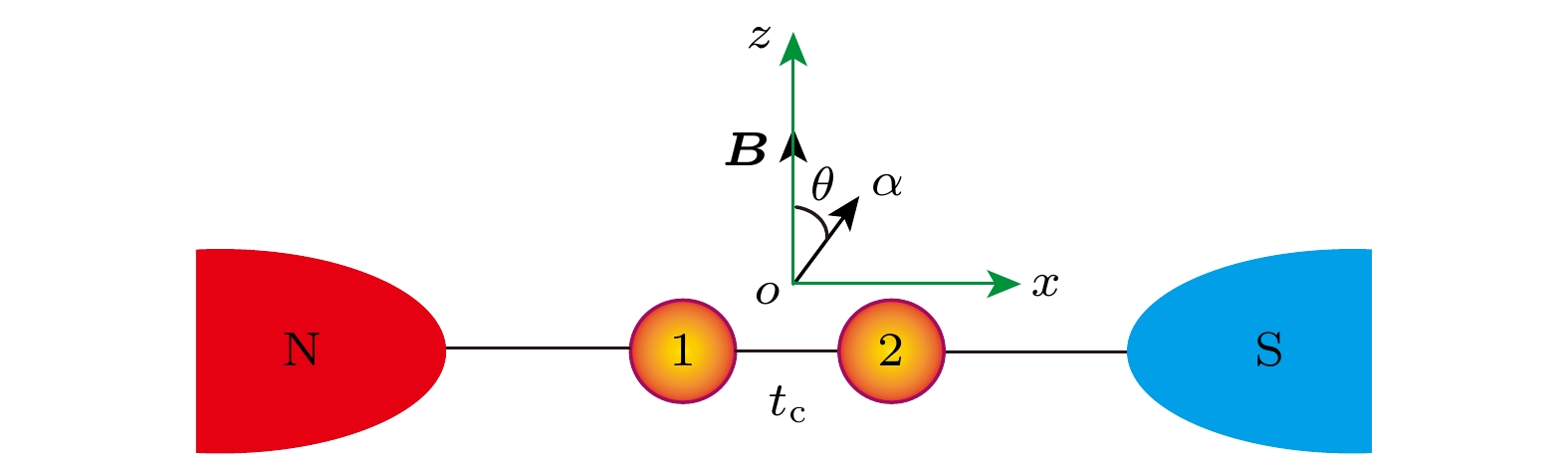
图 1 混合型双量子点结构模型, N表示与量子点1连接的金属电极, S表示与量子点2连接的超导电极, $t_{{\mathrm{c}}}$为量子点之间的耦合强度, θ为自旋-轨道耦合场${\alpha}$与z轴方向的外磁场B 之间的夹角
Fig. 1. Model of hybrid double quantum dots, where N is a normal-metal electrode that is attached to the quantum dot 1, and S represents the superconducting electrode that is connected with the quantum dot 2, $t_{{\mathrm{c}}}$ is the interdot coupling strength, and θ denotes the included angle between the spin-orbit coupling field ${\alpha}$ and the external field B along the z axis.
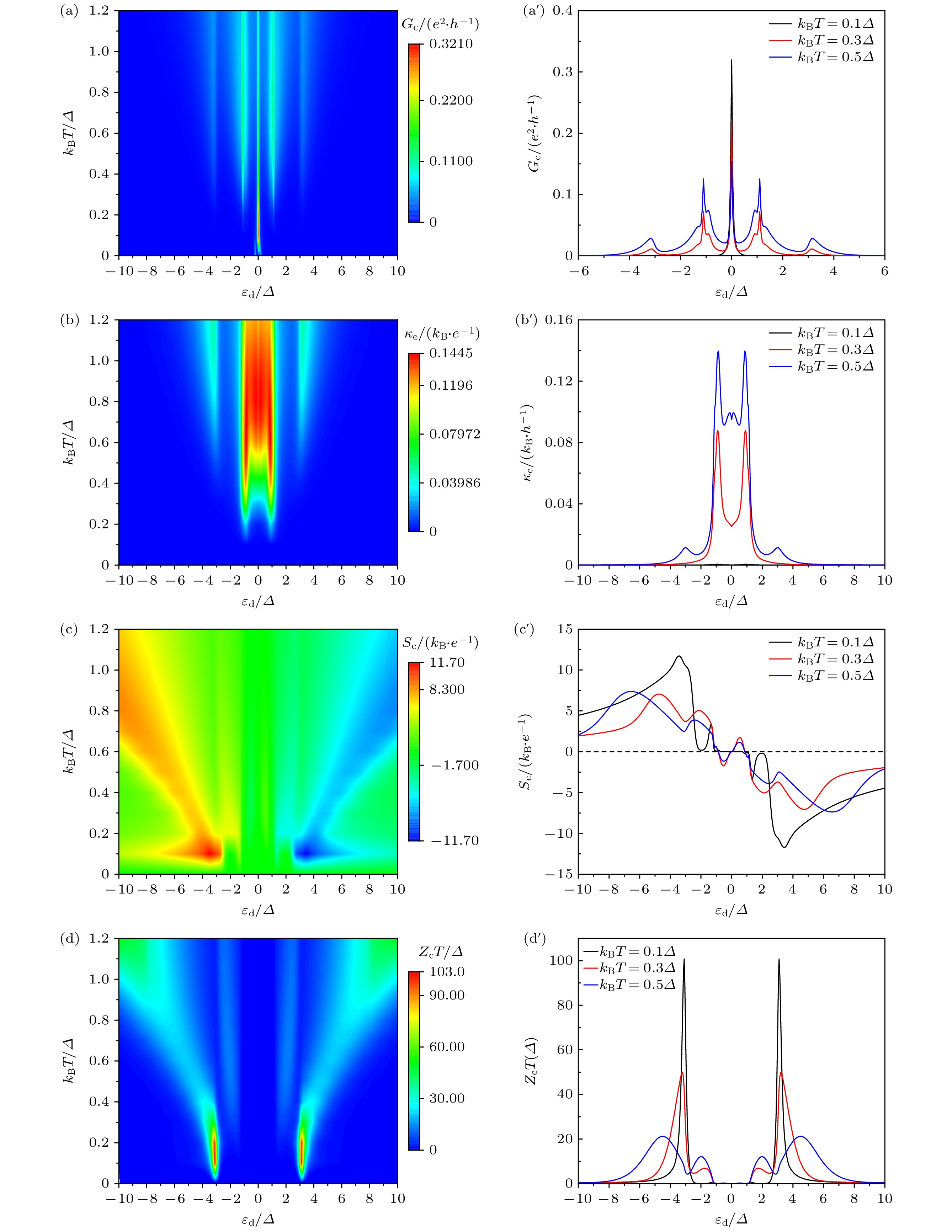
图 2 (a)电导$G_{{\mathrm{c}}}$、(b)热导$\kappa_{{\mathrm{e}}}$、(c)热功率$S_{{\mathrm{c}}}$和 (d)品质因子$Z_{{\mathrm{c}}}T$作为能级$\varepsilon_{{\mathrm{d}}}$与温度$k_{{\mathrm{B}}}T$的函数; 不同温度条件下, (a')电导$G_{{\mathrm{c}}}$、(b')热导$\kappa_{{\mathrm{e}}}$、(c')热功率$S_{c}$和 (d')品质因子$Z_{{\mathrm{{\mathrm{c}}}}}T$的截面图; 其他参数$\alpha=0.2\varDelta$, $\varDelta_{z}=\varDelta$以及$\theta=\pi/2$
Fig. 2. (a) Conductance $G_{{\mathrm{c}}}$, (b) heat conductance $\kappa_{{\mathrm{e}}}$, (c) thermopower $S_{{\mathrm{c}}}$ and (d) figure of merit $Z_{{\mathrm{c}}}T$ as a function of the energy level $\varepsilon_{d}$ and temperature $k_{{\mathrm{B}}}T$ (left column); for different temperatures, the cross sections of (a') conductance $G_{{\mathrm{c}}}$, (b') heat conductance $\kappa_{{\mathrm{e}}}$, (c') thermopower $S_{{\mathrm{c}}}$ and (d') figure of merit $Z_{{\mathrm{c}}}T$ are shown; the other parameters are $\alpha=0.2\varDelta$, $\varDelta_{z}=\varDelta$, and $\theta=\pi/2$.
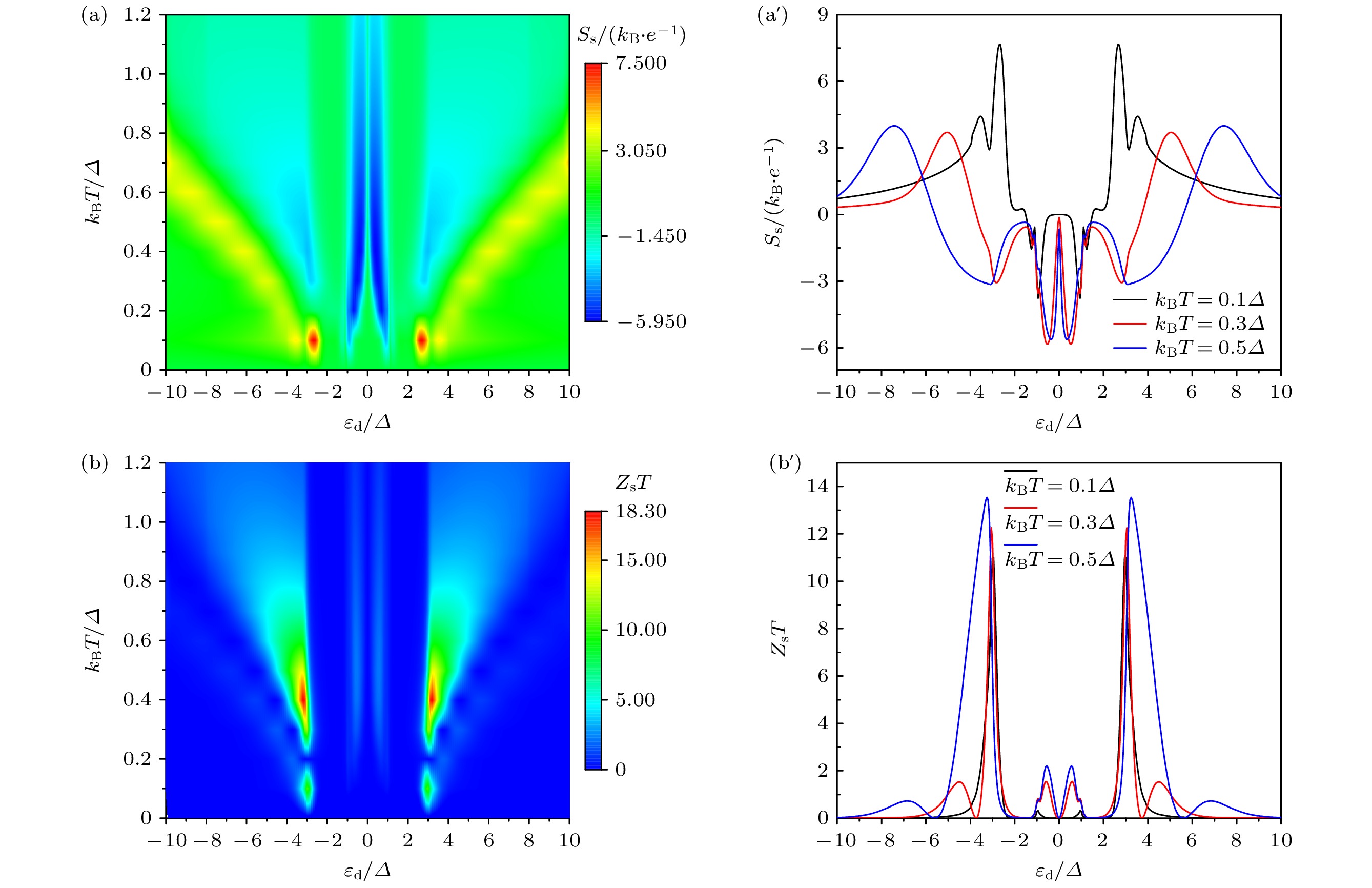
图 3 自旋热电系数(a)热功率$S_{{\mathrm{s}}}$和 (b)品质因子$Z_{{\mathrm{s}}}T$作为能级$\varepsilon_{{\mathrm{d}}}$与温度$k_{{\mathrm{B}}}T$的函数. 不同温度条件下, (a')热功率$S_{{\mathrm{s}}}$和 (b') 品质因子$Z_{{\mathrm{s}}}T$的截面图; 其他参数$\alpha=0.2\varDelta$, $\varDelta_{z}=\varDelta$以及$\theta=\pi/2$
Fig. 3. Spin thermoelectric coefficients (a) thermopower $S_{{\mathrm{s}}}$ and (b) figure of merit $Z_{{\mathrm{s}}}T$ as a function of the energy level $\varepsilon_{{\mathrm{d}}}$ and temperature $k_{{\mathrm{B}}}T$(left column). For different temperatures, the cross sections of (a') thermopower $S_{{\mathrm{c}}}$ and (b') figure of merit $Z_{{\mathrm{s}}}T$ are shown in the right column; the other parameters are $\alpha=0.2\varDelta$, $\varDelta_{z}=1\varDelta$, and $\theta=\pi/2$.
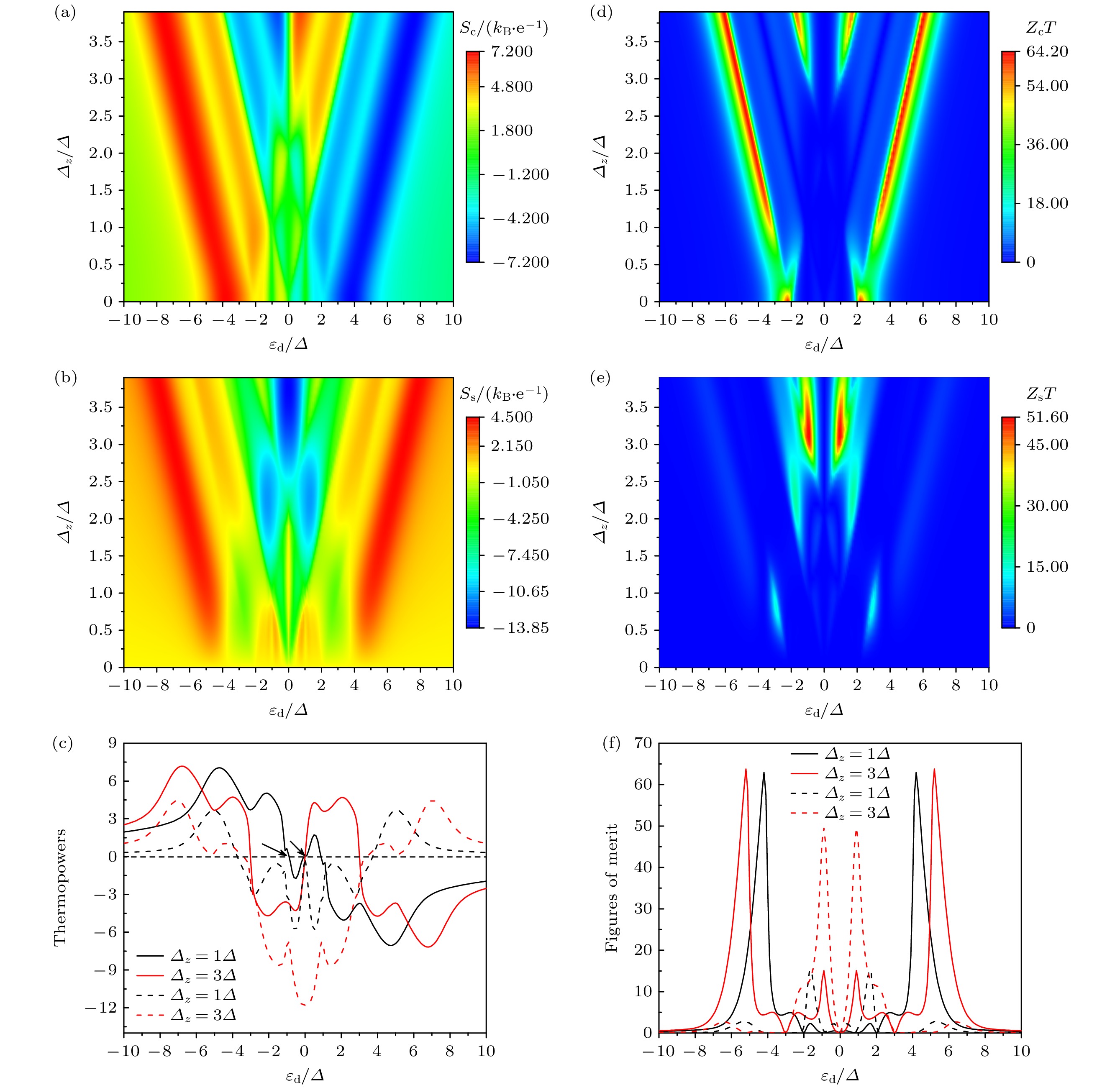
图 4 (a)电荷热功率$S_{{\mathrm{c}}}$和(b)自旋热功率$S_{{\mathrm{s}}}$作为能级$\varepsilon_{{\mathrm{d}}}$与塞曼能$\varDelta_{z}$的函数; (c)不同塞曼能条件下, $S_{{\mathrm{c}}}$(实线)和$S_{{\mathrm{s}}}$(虚线)作为$\varepsilon_{{\mathrm{d}}}$的函数; (d)电荷品质因子$Z_{{\mathrm{c}}}T$和(e)自旋品质因子$Z_{{\mathrm{s}}}T$作为能级$\varepsilon_{{\mathrm{d}}}$与塞曼能$\varDelta_{z}$的函数; (f)不同塞曼能条件下, $Z_{{\mathrm{c}}}T$(实线)和$Z_{{\mathrm{s}}}T$(虚线)作为$\varepsilon_{{\mathrm{d}}}$的函数; 其他参数$\alpha=0.2\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$以及$\theta=\pi/2$
Fig. 4. (a) Charge thermopower $S_{{\mathrm{c}}}$ and (b) spin thermopower $S_{{\mathrm{s}}}$ as a function of the energy level$\varepsilon_{{\mathrm{d}}}$ and the Zeeman energy $\varDelta_{z}$; (c) for different Zeeman energies, $S_{{\mathrm{c}}}$ and $S_{{\mathrm{s}}}$ as a function of the energy level$\varepsilon_{{\mathrm{d}}}$; (d) charge figure of merit $Z_{{\mathrm{c}}}T$ and (e) spin figure of merit $Z_{{\mathrm{s}}}T$ as a function of the energy level $\varepsilon_{{\mathrm{d}}}$ and the Zeeman energy $\varDelta_{z}$; (f) for different Zeeman energies, $Z_{{\mathrm{c}}}T$ and $Z_{{\mathrm{s}}}T$) as a function of the energy level $\varepsilon_{{\mathrm{d}}}$; the other parameters are $\alpha=0.2\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$, and $\theta=\pi/2$.
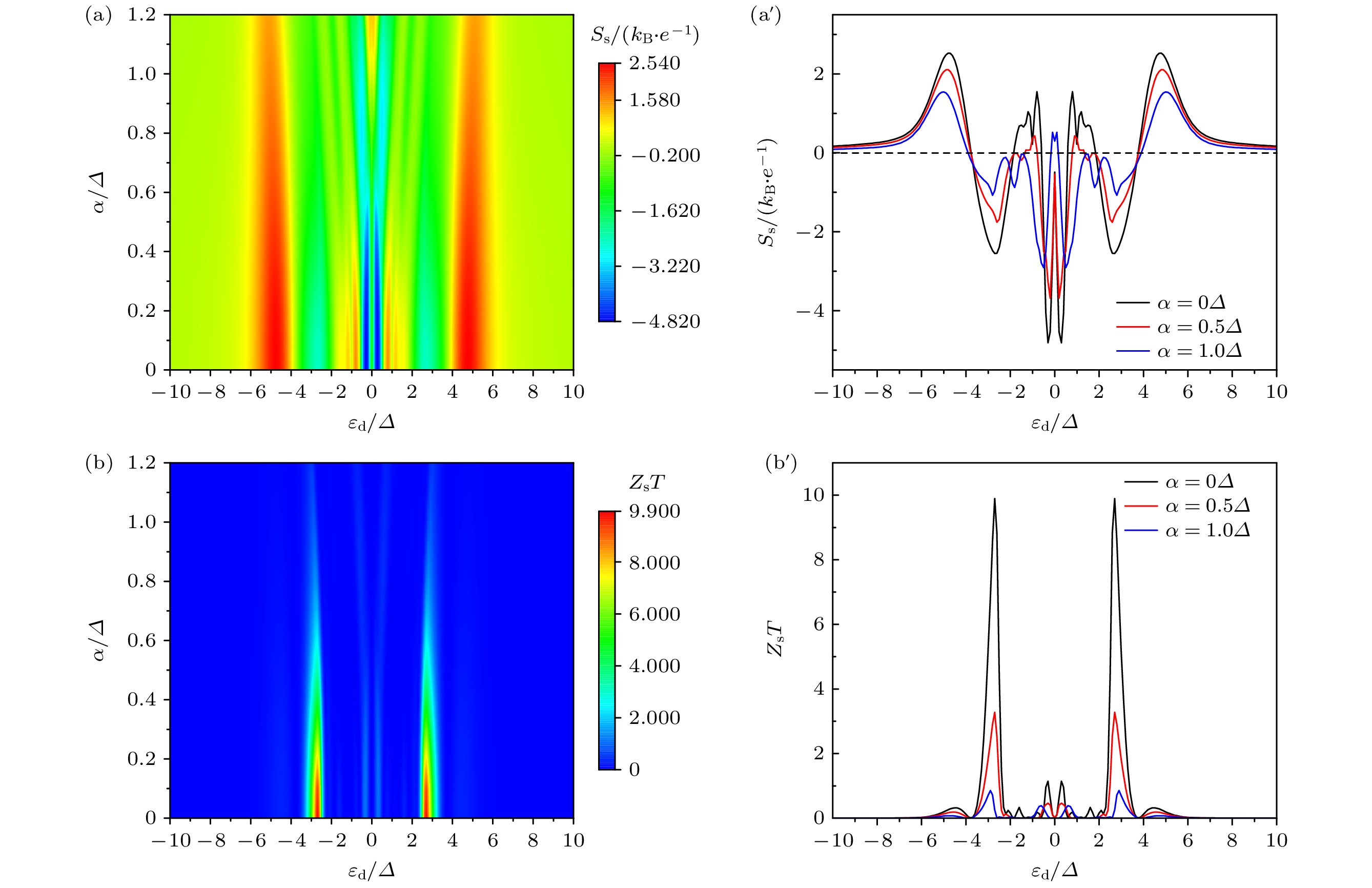
图 5 自旋热电系数(a)热功率$S_{{\mathrm{s}}}$和 (b)品质因子$Z_{{\mathrm{s}}}T$作为能级$\varepsilon_{{\mathrm{d}}}$与自旋-轨道耦合强度α的函数; 不同α条件下, (a')热功率$S_{{\mathrm{s}}}$和 (b') 品质因子$Z_{{\mathrm{s}}}T$的截面图; 其他参数$\varDelta_{z}=0.5\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$以及$\theta=\pi/2$
Fig. 5. Spin thermoelectric coefficients (a) thermopower $S_{{\mathrm{s}}}$ and (b) figure of merit $Z_{{\mathrm{s}}}T$ as a function of the energy level $\varepsilon_{{\mathrm{d}}}$ and spin-orbit coupling strength α (left column); for different temperatures, the cross sections of (a') thermopower $S_{{\mathrm{c}}}$ and (b') figure of merit $Z_{{\mathrm{s}}}T$ are shown, the other parameters are $\varDelta_{z}=0.5\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$, and $\theta=\pi/2$.
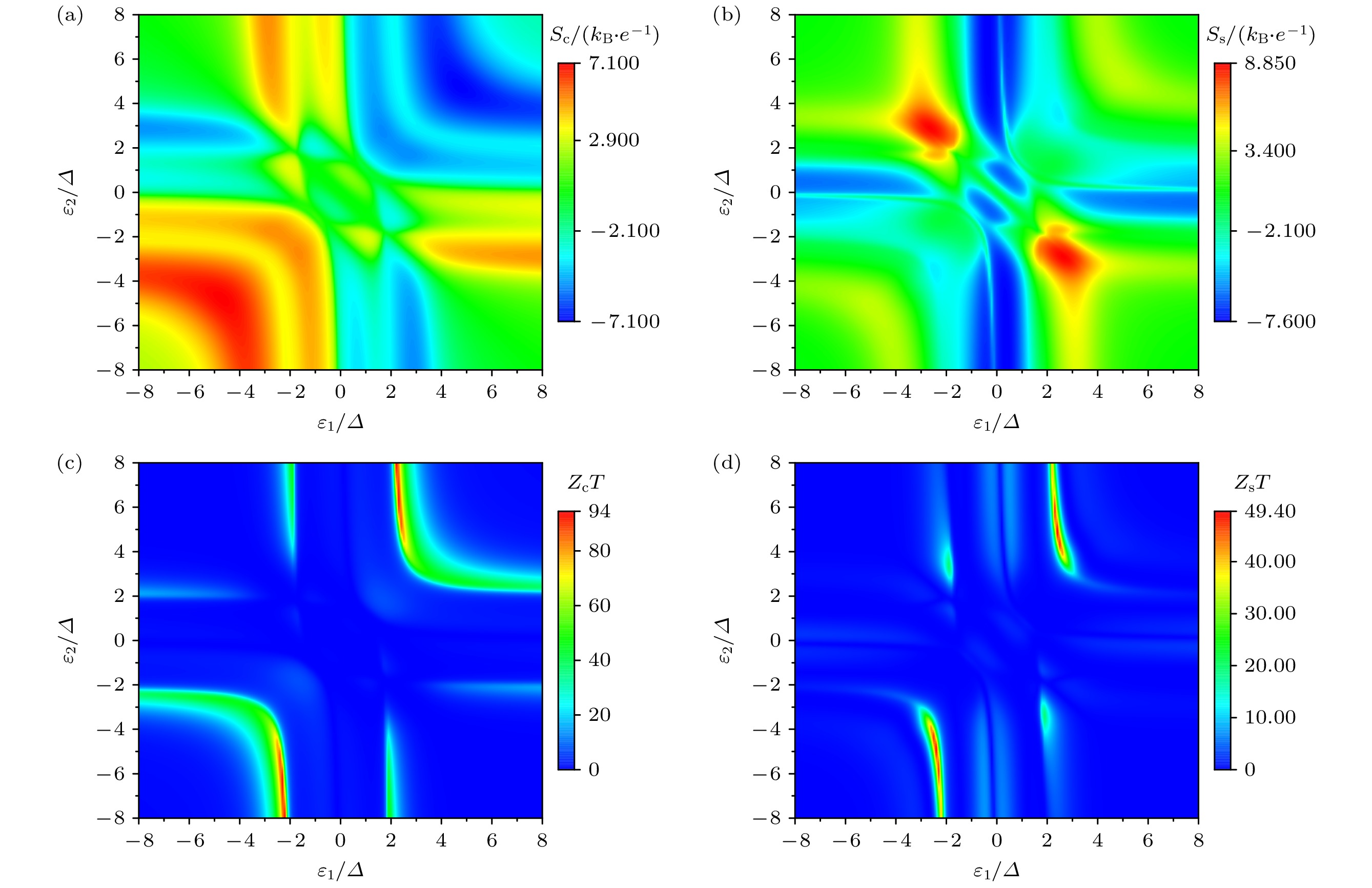
图 6 电荷热电系数(a)热功率$S_{{\mathrm{c}}}$和 (b)品质因子$Z_{{\mathrm{c}}}T$作为量子点能级$\varepsilon_{1}$与$\varepsilon_{2}$的函数; 自旋热电系数 (c)热功率$S_{{\mathrm{s}}}$和 (d) 品质因子$Z_{{\mathrm{s}}}T$作为量子点能级$\varepsilon_{1}$与$\varepsilon_{2}$的函数; 其他参数为$\alpha=0.2\varDelta$, $\varDelta_{z}=\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$以及$\theta=\pi/2$
Fig. 6. Charge thermoelectric coefficients (a) thermopower $S_{{\mathrm{c}}}$ and (c) figure of merit $Z_{{\mathrm{c}}}T$ as a function of the quantum dot’s levels $\varepsilon_{1}$ and $\varepsilon_{2}$; spin thermoelectric coefficients (b) thermopower $S_{{\mathrm{s}}}$ and (d) figure of merit $Z_{{\mathrm{s}}}T$ as a function of the quantum dot’s levels $\varepsilon_{1}$ and $\varepsilon_{2}$; the other parameters are $\alpha=0.2\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$, and $\theta=\pi/2$.
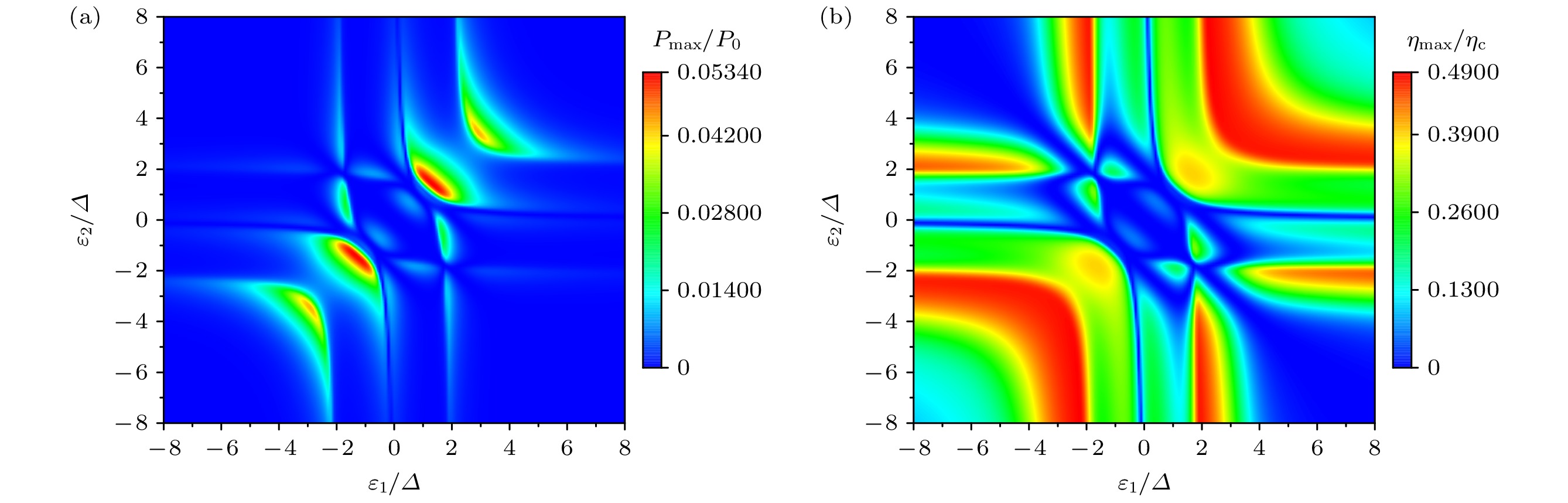
图 7 (a)最大功率$P_{{\mathrm{max}}}$ (以$P_{0}=(k_{{\mathrm{B}}}\varDelta T)^{2}/h$为单位)和(b)最大功率时的效率$\eta_{{\mathrm{max}}P}$ (以卡诺效率$\eta_{{\mathrm{c}}}$为单位) 作为量子点能级$\varepsilon_{1}$与$\varepsilon_{2}$的函数, 其他参数为$\alpha=0.2\varDelta$, $\varDelta_{z}=\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$以及$\theta=\pi/2$
Fig. 7. (a) Maximum power $P_{{\mathrm{max}}}$ (in units of $P_{0}=(k_{{\mathrm{B}}}\varDelta T)^{2}/h$) and (b) efficiency at maximum power $ \eta_{{\mathrm{max}}P}$ (in units of Carnot efficiency $\eta_{{\mathrm{c}}}$) as a function of the quantum dot’s levels $\varepsilon_{1}$ and $\varepsilon_{2}$; the other parameters are $\alpha=0.2\varDelta$, $\varDelta_{z}=\varDelta$, $k_{{\mathrm{B}}}T=0.3\varDelta$ and $\theta=\pi/2$.
-
[1] 陈晓彬, 段文晖 2015 64 186302
 Google Scholar
Google Scholar
Chen X B, Duan W H 2015 Acta Phys. Sin. 64 186302
 Google Scholar
Google Scholar
[2] Mahan G D, Sofo J O 1996 Proc. Natl. Acad. Sci. USA 93 7436
 Google Scholar
Google Scholar
[3] Liu J, Sun Q F, Xie X C 2010 Phys. Rev. B 81 245323
 Google Scholar
Google Scholar
[4] Swirkowicz R, Wierzbicki M, Barnas J 2009 Phys. Rev. B 80 195409
 Google Scholar
Google Scholar
[5] Mazal Y, Meir Y, Dubi Y 2019 Phys. Rev. B 99 075433
 Google Scholar
Google Scholar
[6] Chida K, Fujiwara A, Nishiguchi K 2022 Appl. Phys. Lett. 121 183501
 Google Scholar
Google Scholar
[7] Sanduleac I, Pflaum J, Casian A 2019 J. Appl. Phys. 126 175501
 Google Scholar
Google Scholar
[8] Gomes T C S C, Marchal N, Araujo F A, Piraux L 2019 Appl. Phys. Lett. 115 242402
 Google Scholar
Google Scholar
[9] Wierzbicki M, Swirkowicz R 2010 J. Phys.: Condens. Matter 22 185302
 Google Scholar
Google Scholar
[10] Wang R Q, Shen L, Shen R, Wang B G, Xing D Y 2010 Phys. Rev. Lett. 105 057202
 Google Scholar
Google Scholar
[11] Bao W S, Liu Y S, Lei X L 2010 J. Phys.: Condens. Matter 22 315502
 Google Scholar
Google Scholar
[12] Ghawri B, Mahapatra P S, Garg M, Mandal S, Jayaraman A, Watanabe K, Taniguchi T, Jain M, Chandni U, Ghosh A 2024 Phys. Rev. B 109 045436
 Google Scholar
Google Scholar
[13] Anderson L E, Laitinen A, Zimmerman A, Werkmeister T, Shackleton H, Kruchkov A, Taniguchi T, Watanabe K, Sachdev S, Kim P 2024 Phys. Rev. Lett. 132 246502
 Google Scholar
Google Scholar
[14] Li J, Niquet Y M, Delerue C 2023 Phys. Rev. B 107 245417
 Google Scholar
Google Scholar
[15] Xu Y, Gan Z X, Zhang S C 2014 Phys. Rev. Lett. 112 226801
 Google Scholar
Google Scholar
[16] Blasi G, Taddei F, Arrachea L, Carrega M, Braggio A 2020 Phys. Rev. Lett. 124 227701
 Google Scholar
Google Scholar
[17] Sebastian Bergeret F, Silaev M, Virtanen P, Heikkilä T T 2018 Rev. Mod. Phys. 90 041001
 Google Scholar
Google Scholar
[18] Hwang S Y, Lopez R, Sanchez D 2016 Phys. Rev. B 94 054506
 Google Scholar
Google Scholar
[19] Hwang S Y, Sanchez D, Lopez R 2016 New. J. Phys. 18 093024
 Google Scholar
Google Scholar
[20] Trocha P, Barnas J 2017 Phys. Rev. B 95 165439
 Google Scholar
Google Scholar
[21] Michaek G, Urbaniak M, Bulka B R, Domanski T, Wysokinski K I 2016 Phys. Rev. B 93 235440
 Google Scholar
Google Scholar
[22] Dutta P, Alves K R, Black-Schaffer A M 2020 Phys. Rev. B 102 094513
 Google Scholar
Google Scholar
[23] Linder J, Balatsky A V 2019 Rev. Mod. Phys. 91 045005
 Google Scholar
Google Scholar
[24] Kubala B, Konig J 2002 Phys. Rev. B 65 245301
 Google Scholar
Google Scholar
[25] Chi F, Li S S 2006 J. Appl. Phys. 100 113703
 Google Scholar
Google Scholar
[26] Kang K, Cho S Y 2004 J. Phys.: Condens. Matter 16 117
 Google Scholar
Google Scholar
[27] Lu H Z, Lü R, Zhu B F 2005 Phys. Rev. B 71 235320
 Google Scholar
Google Scholar
[28] Kubo T, Tokura Y, Tarucha S 2011 Phys. Rev. B 83 115310
 Google Scholar
Google Scholar
[29] Pan H, Lin T H 2006 Phys. Rev. B 74 235312
 Google Scholar
Google Scholar
[30] Bordoloi A, Zannier V, Sorba L, Schrnenberger C, Baumgartner A 2020 Commun. Phys. 3 135
 Google Scholar
Google Scholar
[31] Bittermann L, Dominguez F, Recher P 2024 Phys. Rev. B 110 045429
 Google Scholar
Google Scholar
[32] Bułka B R 2022 Phys. Rev. B 106 085424
 Google Scholar
Google Scholar
[33] Yao H, Zhang C, Li Z J, Nie Y H, Niu P B 2018 J. Phys. D: Appl. Phys. 51 175301
 Google Scholar
Google Scholar
[34] Bai L, Zhang L, Tang F R, Zhang R 2023 J. Appl. Phys. 134 184304
 Google Scholar
Google Scholar
[35] Hussein R, Governale M, Sigmund Kohler S, Belzig W, Giazotto F, Alessandro Braggio A 2019 Phys. Rev. B 99 075429
 Google Scholar
Google Scholar
[36] Tabatabaei S M, Sánchez D, Yeyati A L, Sánchez R 2022 Phys. Rev. B 106 115419
 Google Scholar
Google Scholar
[37] Sánchez R, Burset P, Yeyati A L 2018 Phys. Rev. B 98 241414
 Google Scholar
Google Scholar
[38] Gresta D, Real M, Arrachea L 2019 Phys. Rev. Lett. 123 186801
 Google Scholar
Google Scholar
计量
- 文章访问数: 1022
- PDF下载量: 55
- 被引次数: 0













 下载:
下载: