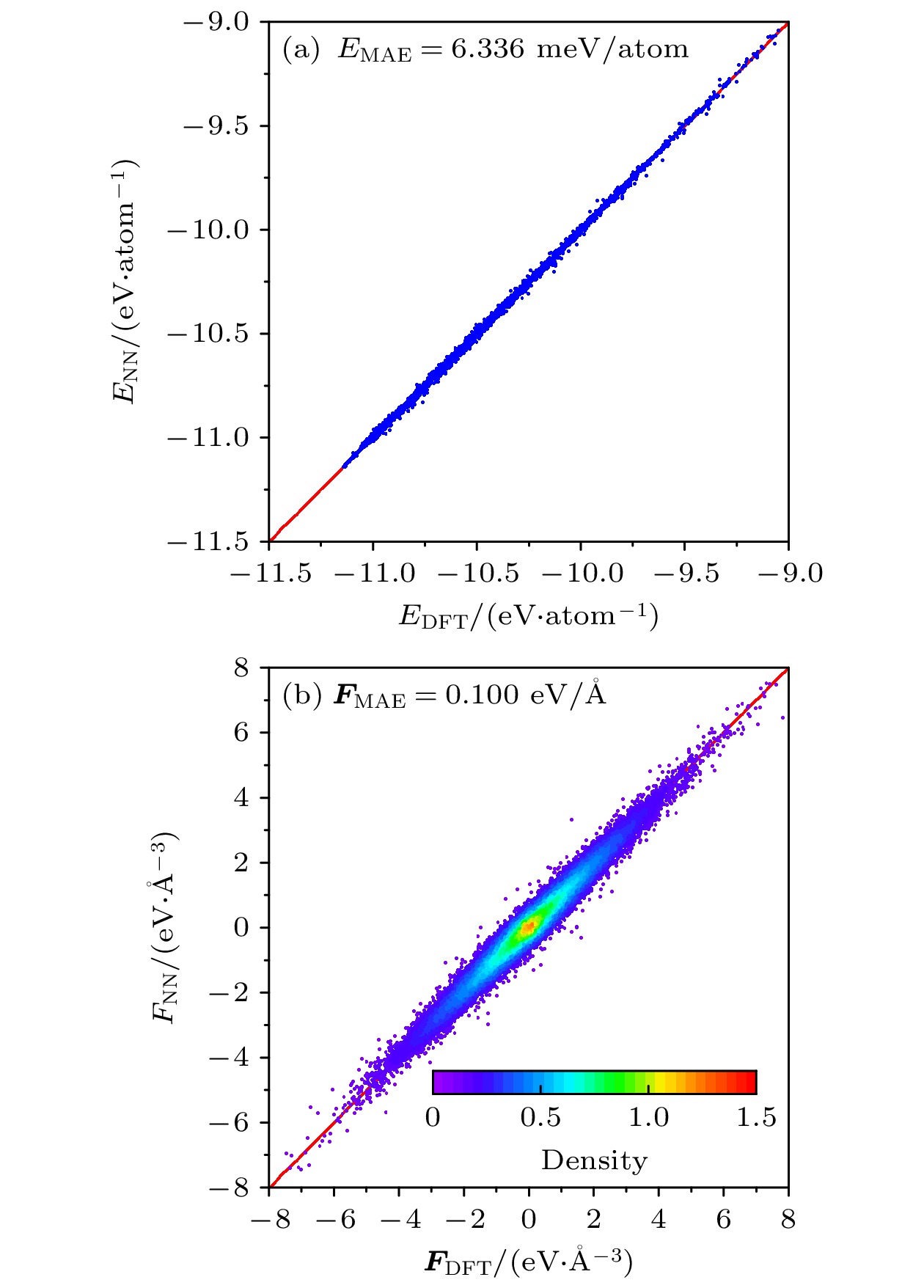
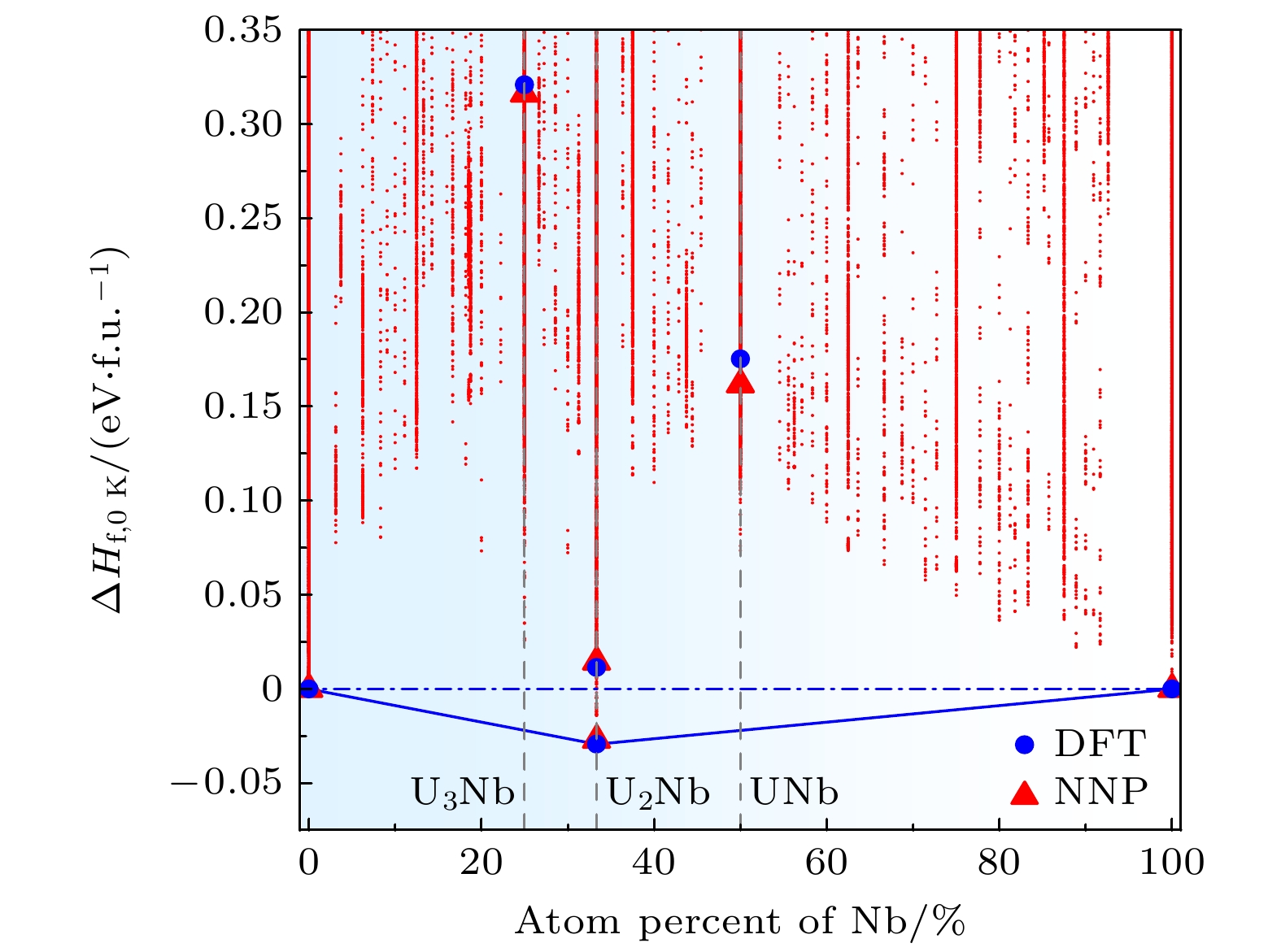
-
铀铌合金在不同实验环境中呈现出复杂的晶体相和独特的力学性能, 但原子尺度的相析出和形变损伤机制尚不清楚, 其根本原因是缺乏支撑大尺度分子动力学模拟的精确铀铌合金原子相互作用势. 本工作基于自主开发的神经网络势能函数及随机搜索方法, 构建了覆盖全化学空间的铀铌合金第一性原理计算数据库, 并基于神经网络框架建立了具有较高泛化性能和精度的铀铌二元体系机器学习势函数, 其能量和力的测试平均绝对误差分别为5.6 meV/atom和0.095 eV/Å, 可以精确地描述不同化学成分铀铌合金的晶体空间结构, 状态方程及热力学参量. 基于该势函数, 我们实现了低温时效下铀铌合金相失稳分解过程的原子尺度模拟, 初步阐明了Nb析出相对其合金力学性能的影响及原子响应机制.
Uranium-niobium alloys exhibit complex crystal phases and unique mechanical behaviors under various thermodynamic states and external loads. However, due to the lack of accurate interatomic potentials, the atomic-scale phase behaviors and dynamical processes in this important alloy are still unclear. In recent years, the development of machine-learning-based force fields has provided a systematic way to generate accurate interatomic potentials on large and complex first-principle-based datasets. However, this crucial nuclear material has received limited attention from researchers in the field of machine-learning potentials. In this work, based on our previous researches on the neural-network potential training and evaluation framework, which we called NNAP, a new neural network potential is constructed for the uranium-niobium alloy system. A combination of random structure search and active learning algorithms is utilized to enhance coverage of the chemical and structural space of the alloy system. Testing of the generated potential demonstrates high generalization performance and accuracy. On the testing set, the mean absolute error of the energy and the force are 5.6 meV/atom and 0.095 eV/Å, respectively. Further calculation results of crystal structure parameters, equation of state, and phonon dispersions coincide well with the results from the first-principle or experimental references. The atomic-scale evolution of the spinodal decomposition process in the U-Nb alloys is investigated based on the newly trained potential. It is shown that the atom-swapping hybrid Monte Carlo can be a powerful tool to understand the thermodynamic evolution of the systems. By using the atom-swapping hybrid Monte Carlo method, the decrease of potential energy due to phase segregation is observed within 5000 steps, while no significant energy reduction is found after 3-ns MD simulation. Finally, the stress-strain curves under shear load for different initial states are obtained. It is found that the Nb precipitation generates strengthened phases in the alloy and the deformation behavior of U-Nb alloys is significantly changed, where a disorder shear band emerges in the deformation path of the $ {\mathrm{\gamma }} $-phase alloys. Our work lays a foundation for understanding the mechanical processes in this important alloy system. 
-
Keywords:
- uranium-niobium alloys /
- neural network potential /
- molecular dynamics /
- mechanical properties
-
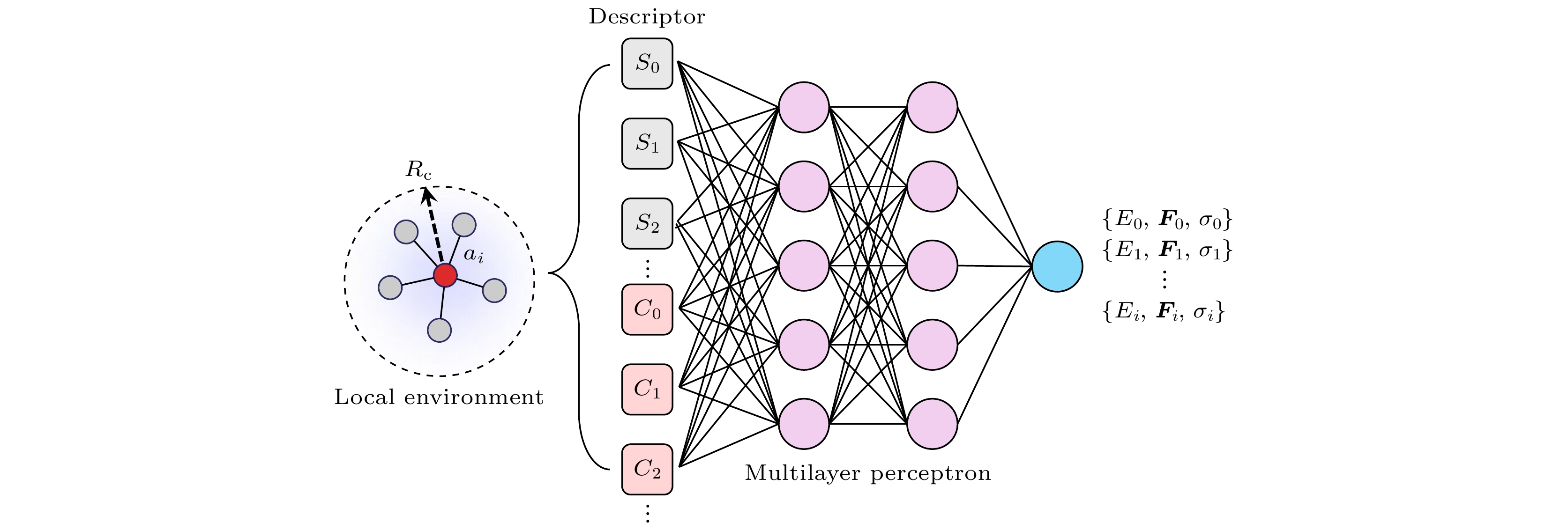
图 1 神经网络势能函数基本架构. $ {S}_{i} $和$ {C}_{i} $分别为未考虑和考虑化学权重后的局域原子描述符. 训练集中结构的原子局域环境描述符是包含多个隐藏层的多层感知机模型的输入参量, 在输出端可获得原子势能、力以及原子应力
Fig. 1. The basic architecture of the neural network potential function. $ {S}_{i} $ and $ {C}_{i} $ represent the local atomic descriptors before and after considering chemical weights, respectively. The atomic local environment descriptors of structures in the training set serve as input parameters to a multi-layer perceptron model with multiple hidden layers. The output provides the atomic potential energy, forces, and atomic stress.
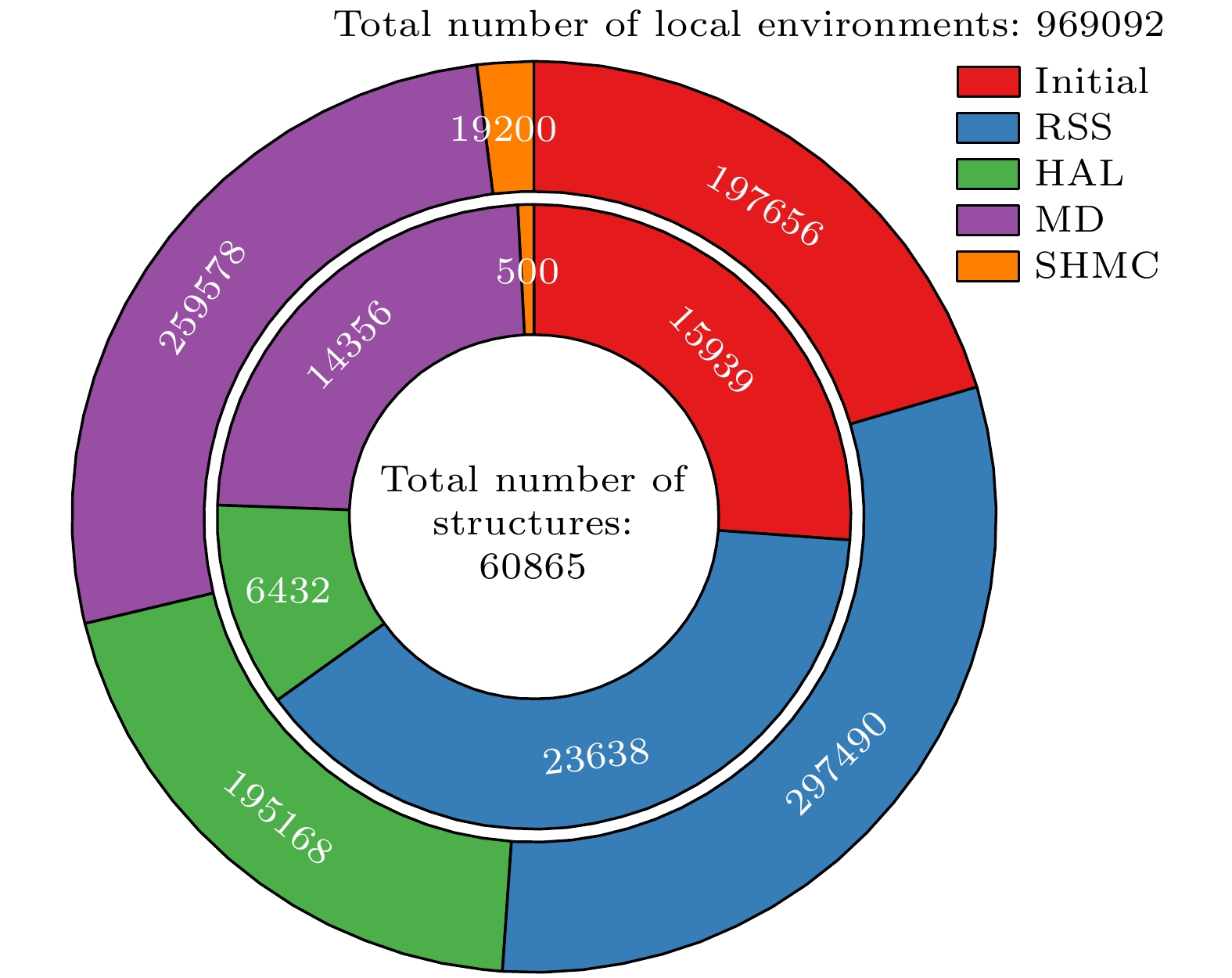
图 2 训练集中不同来源数据的占比及分布. 内圈为结构数目, 外圈为局域环境数目(原子数). Initial为初始数据集, RSS为随机结构搜索数据集, HAL为主动学习数据集, MD为分子动力学数据集, SHMC为原子交换蒙特卡洛数据集
Fig. 2. The proportion and distribution of data from different sources in the whole training set. The inner circle represents the number of structures, while the outer circle represents the number of local environments (atoms). Initial refers to the initial dataset, RSS to the random structure search dataset, HAL to the active learning dataset, MD to the molecular dynamics simulation dataset, and SHMC to the atomic swap Monte Carlo dataset.
图 3 铀铌合金势能函数测试精度 (a) 原子势能测试精度; (b) 力分量测试精度. 图(b)中数据点颜色代表局域数密度
Fig. 3. Test set accuracy of trained U-Nb potential: (a) MAE of potential energies; (b) MAE of force components. The color of each point in (b) represents the local density.
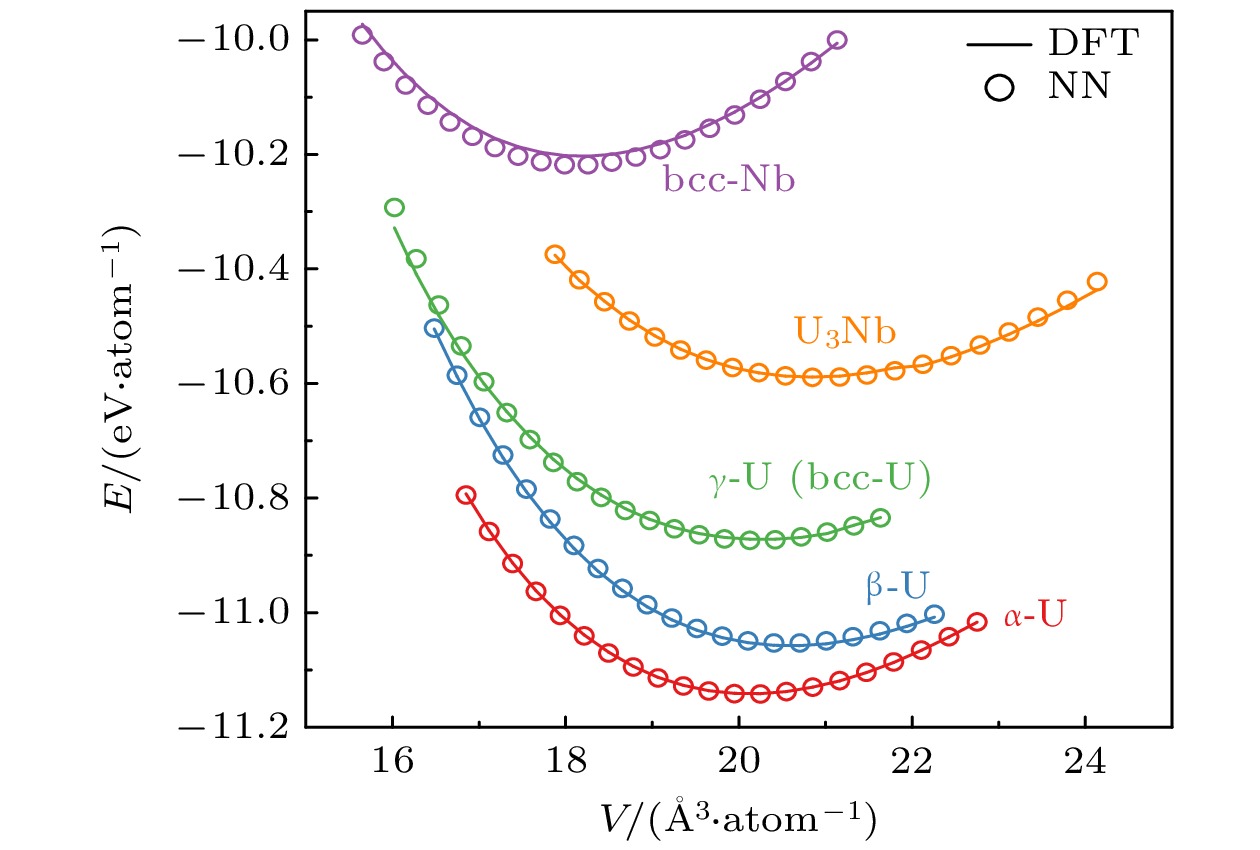
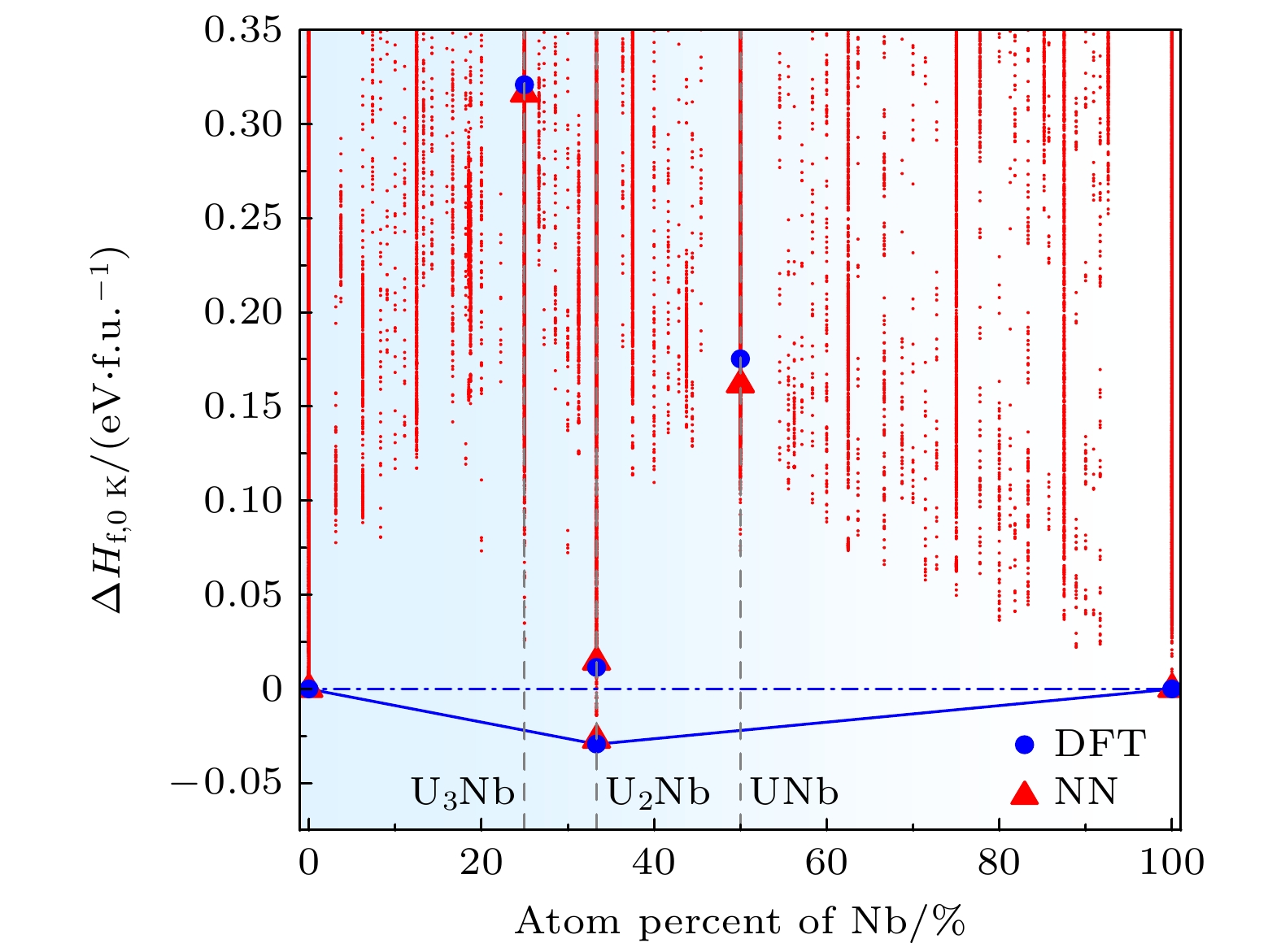
图 4 铀铌合金体系状态方程. 实线和空心圆圈分别代表DFT和NNP计算结果. $ {{\mathrm{U}}}_{3}{\mathrm{N}}{\mathrm{b}} $的结构取自Materials project网站, 结构编号为mp-972551
Fig. 4. Equation of states of U-Nb alloy. Solid and empty circles represent the DFT and NNP results, respectively. The U3Nb structure is obtained from the Materials project website with an id of mp-972551.
图 5 0 K下铀铌二元合金成分相图. 蓝色圆点为第一性原理计算结果, 红色三角形为NNP计算结果, 红色点为数据集中的结构能量
Fig. 5. Composition phase diagram of U-Nb phase diagram at 0 K. The blue filled circles and red filled triangles show the DFT and NNP results, respectively. The red points correspond to training structure energies in the training set.
图 6 DFT及NNP计算得到的晶体声子能带色散曲线
Fig. 6. Phonon dispersion curves of $ \alpha -{\mathrm{U}} $, $ \gamma -{\mathrm{U}} $ and $ \gamma -{\mathrm{N}}{\mathrm{b}} $ calculated by DFT (red lines) and NNP (blue lines).
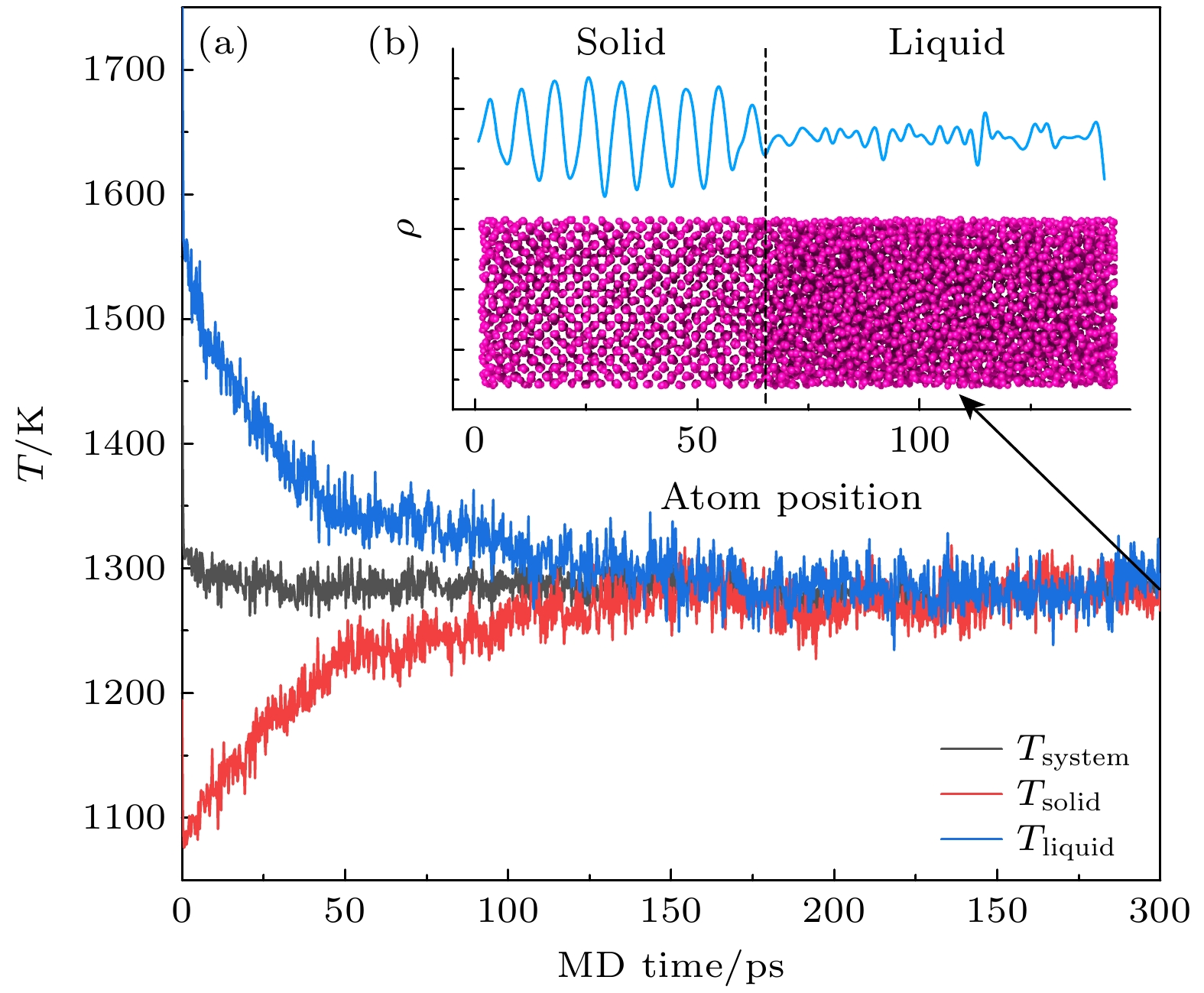
图 7 $ \gamma {\mathrm{铀}} $的相固-液相平衡模拟 (a)体系平均温度及固体和液体部分的温度; (b)平衡构型中x方向原子数密度的空间变化以及固-液界面原子结构. 计算得到的熔点(固-液平衡点)为(1286±9) K
Fig. 7. Calculated melting point of $ {\mathrm{\gamma }} $-U: (a) Temperature evolution of whole, liquid and solid part of system; (b) number density evolution along the x direction, showing a sharp solid-liquid interface in coordinate to the MD snapshot. The calculated melting point is (1286±9) K.
图 9 铀铌合金$ \alpha $相与$ \gamma $相的相对热力学稳定性. 实线为三次多项式拟合结果
Fig. 9. Relative phase stability of $ \alpha $ and $ \gamma $ phase against the atomic percentage of Nb element. Solid line shows the third order polynomial fitting.
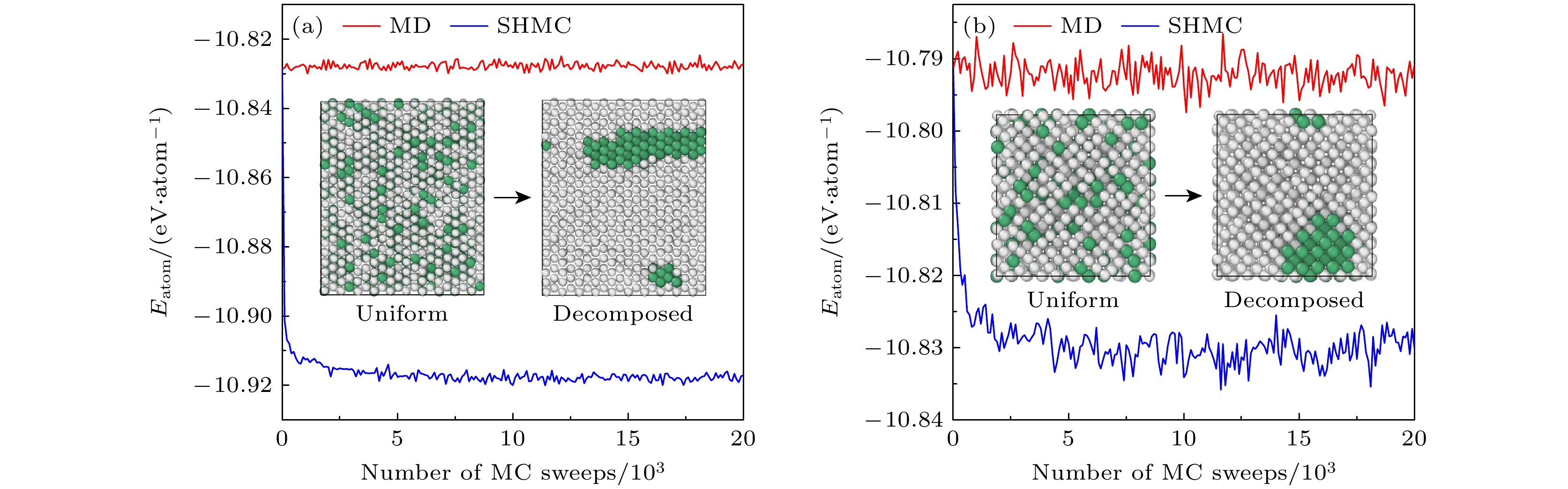
图 10 $ 600{\mathrm{ }}{\mathrm{K}} $模拟时效下Nb原子百分数为13%的铀铌合金的相失稳分离现象 (a) $ \alpha $-U相势能和结构的演化; (b) $ \gamma $-U相势能和结构的演化. 白色小球和绿色小球分别代表铀原子和铌原子
Fig. 10. Spinodal decomposition of U-Nb alloy with an atomic percentage content of 13% aged at $ T=600{\mathrm{K}} $ (a) Potential energy and structure evolutions of $ \alpha $-U phase; (b) potential energy and structure evolutions in $ \gamma $-U phase. The uranium and niobium atoms are shown as white and green balls, respectively.
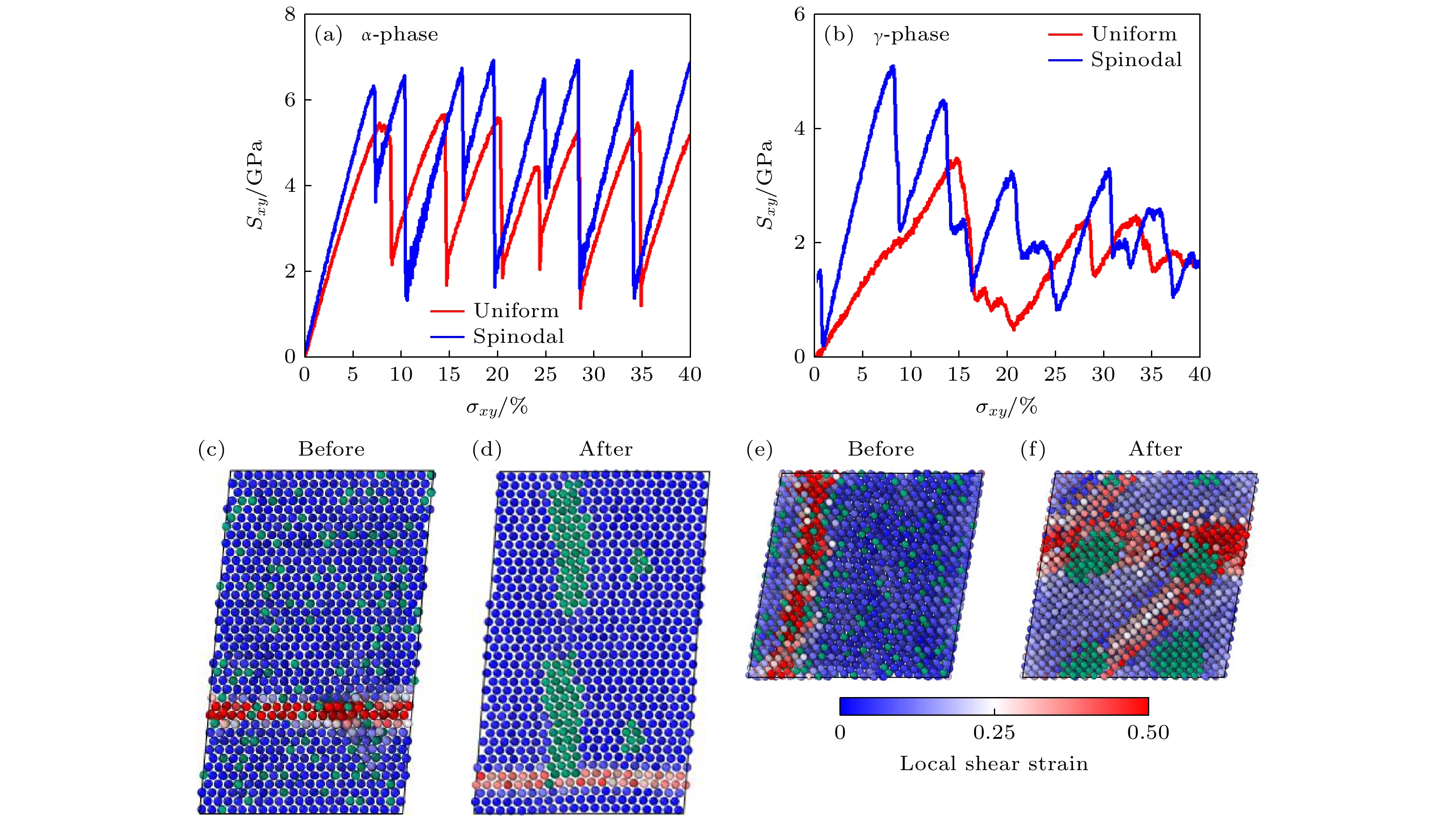
图 11 室温(300 K)下不同初始结构Nb原子百分数为13%的铀铌合金剪切应变下的变形损伤 (a), (b)均匀与相分离后$ \alpha $和$ \gamma $铀铌合金的应力应变关系; (c) $ \alpha $铀铌合金相分离前后塑性变形的原子机制; (d) $ \gamma $铀铌合金相分离前后塑性变形的原子响应机制. 其中Nb原子由绿色圆球表示, U原子的颜色代表局域剪切应变
Fig. 11. Deformation and damage of U-Nb alloys with a Nb atomic percentage content of 13% under shear strain at room temperature (300 K) with different initial structures: (a), (b) Stress-strain relationships of uniform and phase-separated α and γ uranium-niobium alloys; (c) atomic mechanisms of plastic deformation in α uranium-niobium alloy before and after phase decomposition; (d) atomic response mechanisms of plastic deformation in γ uranium-niobium alloy before and after phase decomposition. Niobium atoms are represented by green balls, and the color of uranium atoms indicates local shear strain[44].
表 1 NNP计算得到的晶格参数与第一性原理计算及实验测量结果的比较
Table 1. Computed lattice constants for various crystalline phases, compared with experimental results.
晶体相 晶格参数/Å DFT NNP Exp. $ \alpha -{\mathrm{U}} $ $ a $ 2.806 2.809 (+0.10%) 2.836[40] $ b $ 5.836 5.854 (+0.32%) 5.867[40] $ c $ 4.908 4.893 (–0.31%) 4.935[40] $ \gamma -{\mathrm{U}} $ $ a $ 3.435 3.431 (–0.12%) 3.47[41] $ \gamma -{\mathrm{N}}{\mathrm{b}} $ $ a $ 3.308 3.309 (+0.03%) 3.3063[42] $ {{\mathrm{U}}}_{2}{\mathrm{N}}{\mathrm{b}} $ $ a $ 4.806 4.799 (–0.15%) — $ c $ 5.903 5.914 (0.18%) — 
下载: 导出CSV
-
[1] Vandermeer R A 1980 Acta Metall. 28 383
Google Scholar
[2] Clarke A J, Field R D, Hackenberg R E, Thoma D J, Brown D W, Teter D F, Miller M K, Russell K F, Edmonds D V, Beverini G 2009 J. Nucl. Mater. 393 282
Google Scholar
[3] Vandermeer R A, Ogle J C, Snyder W B 1978 Scr. Metall. 12 243
Google Scholar
[4] Field R D, Brown D W, Thoma D J 2005 Philos. Mag. 85 2593
Google Scholar
[5] Zhang C, Wang H, Li J, Pang B, Xia Y, Liu Y, Sun G, Zhang X, Fa T, Wang X 2019 Mater. Des. 162 94
Google Scholar
[6] Choung S, Park W, Moon J, Han J W 2024 Chem. Eng. J. 494 152757
Google Scholar
[7] Ma S, Liu Z P 2020 ACS Catal. 10 13213
Google Scholar
[8] Su R, Yu J, Guan P, Wang W 2024 Sci. Chin. Mater. 67 3298
Google Scholar
[9] Shapeev A V 2016 Multiscale Model. Simul. 14 1153
Google Scholar
[10] Artrith N, Urban A, Ceder G 2018 J. Chem. Phys. 148 241711
Google Scholar
[11] Behler J, Parrinello M 2007 Phys. Rev. Lett. 98 146401
Google Scholar
[12] Chiriki S, Jindal S, Bulusu S S 2017 J. Chem. Phys. 146 084314
Google Scholar
[13] Zhao R, Wang S, Kong Z, Xu Y, Fu K, Peng P, Wu C 2023 Mater. Des. 231 112012
Google Scholar
[14] Young T A, Johnston-Wood T, Deringer V L, Duarte F 2021 Chem. Sci. 12 10944
Google Scholar
[15] Smith J S, Nebgen B, Lubbers N, Isayev O, Roitberg A E 2018 J. Chem. Phys. 148 241733
Google Scholar
[16] van der Oord C, Sachs M, Kovács D P, Ortner C, Csányi G 2023 npj Comput. Mater. 9 1
Google Scholar
[17] Kulichenko M, Barros K, Lubbers N, Li Y W, Messerly R, Tretiak S, Smith J S, Nebgen B 2023 Nat. Comput. Sci. 3 230
Google Scholar
[18] Deringer V L, Pickard C J, Csányi G 2018 Phys. Rev. Lett. 120 156001
Google Scholar
[19] Hao M S, Guan P F 2023 Chin. Phys. B 32 098401
Google Scholar
[20] Li F, Zhang Z, Liu H, Zhu W, Wang T, Park M, Zhang J, Bönninghoff N, Feng X, Zhang H, Luan J, Wang J, Liu X, Chang T, Chu J P, Lu Y, Liu Y, Guan P, Yang Y 2024 Nat. Mater. 23 52
Google Scholar
[21] Zhang Z, Zhang S, Wang Q, Lu A, Chen Z, Yang Z, Luan J, Su R, Guan P, Yang Y 2024 Proc. Natl. Acad. Sci. U. S. A. 121 e2400200121
Google Scholar
[22] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[23] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[24] Adak S, Nakotte H, de Châtel P F, Kiefer B 2011 Phys. B: Condens. Matter. 406 3342
Google Scholar
[25] Bartók A P, Kondor R, Csányi G 2013 Phys. Rev. B 87 184115
Google Scholar
[26] Jindal S, Chiriki S, Bulusu S S 2017 J. Chem. Phys. 146 204301
Google Scholar
[27] Gasteiger J, Groß J, Günnemann S 2022 arXiv: 2003.03123 [cs. LG]
[28] Artrith N, Urban A, Ceder G 2017 Phys. Rev. B 96 014112
Google Scholar
[29] Loshchilov I, Hutter F 2019 arXiv: 1711.05101 [cs. LG]
[30] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[31] Thompson A P, Aktulga H M, Berger R, Bolintineanu D S, Brown W M, Crozier P S, in ’t Veld P J, Kohlmeyer A, Moore S G, Nguyen T D, Shan R, Stevens M J, Tranchida J, Trott C, Plimpton S J 2022 Comput. Phys. Commun. 271 108171
Google Scholar
[32] Nosé S 1984 J. Chem. Phys. 81 511
Google Scholar
[33] Parrinello M, Rahman A 1980 Phys. Rev. Lett. 45 1196
Google Scholar
[34] Zhang L, Han J, Wang H, Car R, E W 2018 Phys. Rev. Lett. 120 143001
Google Scholar
[35] Wen T, Wang C Z, Kramer M J, Sun Y, Ye B, Wang H, Liu X, Zhang C, Zhang F, Ho K M, Wang N 2019 Phys. Rev. B 100 174101
Google Scholar
[36] Pickard C J, Needs R J 2011 J. Phys. Condens. Matter 23 053201
Google Scholar
[37] Imbalzano G, Anelli A, Giofré D, Klees S, Behler J, Ceriotti M 2018 J. Chem. Phys. 148 241730
Google Scholar
[38] Mahoney M W, Drineas P 2009 Proc. Natl. Acad. Sci. U. S. A. 106 697
Google Scholar
[39] Pan X L, Wang H, Zhang L L, Wang Y F, Chen X R, Geng H Y, Chen Y 2023 J. Nucl. Mater. 579 154394
Google Scholar
[40] Barrett C S, Mueller M H, Hitterman R L 1963 Phys. Rev. 129 625
Google Scholar
[41] Wilson A S, Rundle R E 1949 Acta Cryst. 2 126
Google Scholar
[42] Roberge R 1975 J. Less-Common Met. 40 161
Google Scholar
[43] Koike J, Kassner M E, Tate R E, Rosen R S 1998 J. Phase Equilib. 19 253
Google Scholar
[44] Shimizu F, Ogata S, Li J 2007 Mater. Trans. 48 2923
Google Scholar
下载:
计量
- 文章访问数: 382
- PDF下载量: 6
- 被引次数: 0
