-
利用数值模拟含时薛定谔方程的方法, 研究了氢原子在强激光场作用下产生的阈下高次谐波辐射. 在波长为608 nm激光作用下, 氢原子可以吸收5个光子, 由基态$\left|1s\right\rangle$ 共振跃迁至激发态$\left|2p\right\rangle$ 态; 氢原子也可以吸收更多光子发生电离, 某些连续态$\left|c\right\rangle$ 在激光缀饰下其能量可以和$\left|2p\right\rangle$ 态能量相当. 随后发生的$\left|2p\right\rangle$态到$\left|1s\right\rangle$ 态的复合, 或$\left|c\right\rangle$ 态到$\left|1s\right\rangle$ 态的复合, 可辐射出能量相同的光子. 这两个复合路径相互干涉, 在第五次谐波中形成典型的法诺线形. 进一步研究发现, 该法诺线形依赖于激光强度. 本研究表明, 即便是在单电子体系中, 法诺干涉也可以存在, 并可以通过控制激光参数改变法诺线形.We numerically solved the time-dependent Schrödinger equation (TDSE) for a hydrogen atom interacting with intense near-infrared laser fields to investigate the mechanism of below-threshold high-harmonic generation (HHG). The primary focus was on understanding the spectral features, particularly resonant structures, arising in the fifth harmonic region under specific driving conditions. Our simulations utilized a laser wavelength of 608 nm. At this wavelength, hydrogen atoms can resonantly absorb five photons, promoting electrons from the ground state $\left|1s\right\rangle$ to the excited state $\left|2p\right\rangle$. Concurrently, atoms can absorb additional photons leading to ionization. Crucially, due to the AC Stark shift induced by the intense laser field (laser dressing), certain laser-dressed continuum states $\left|c\right\rangle$ become energetically degenerate with the laser-dressed $\left|2p\right\rangle$ state. High-harmonic radiation at the fifth harmonic frequency can then be emitted via two distinct quantum paths: (1) Bound-bound recombination: Direct recombination from the laser-dressed $\left|2p\right\rangle$ state back to the ground state $\left|1s\right\rangle$. (2) Continuum-bound recombination: Recombination from the laser-dressed continuum states $\left|c\right\rangle$ (reached via ionization) back to $\left|1s\right\rangle$. Both pathways emit photons of identical energy corresponding to the fifth harmonic. Our key finding is the pronounced quantum interference between these two recombination channels. This interference manifests spectrally as a characteristic asymmetric Fano lineshape in the intensity profile of the fifth harmonic. Furthermore, we demonstrate that the shape of this Fano resonance exhibits a strong and controllable dependence on the intensity of the driving laser field. This study provides clear evidence that Fano quantum interference, typically associated with multi-electron correlations or autoionizing states in complex systems, can emerge in the fundamental single-electron hydrogen atom system under intense laser fields. The interference arises directly from the coherent superposition of the bound-bound and continuum-bound recombination pathways enabled by laser-induced degeneracy. Importantly, the spectral profile of the Fano resonance can be actively manipulated by tuning the laser intensity, highlighting a novel avenue for coherent control of harmonic emission in simple atomic systems.
-
Keywords:
- Hydrogen atom /
- Intense laser field /
- Below-threshold high-harmonic generation /
- Fano resonance
-
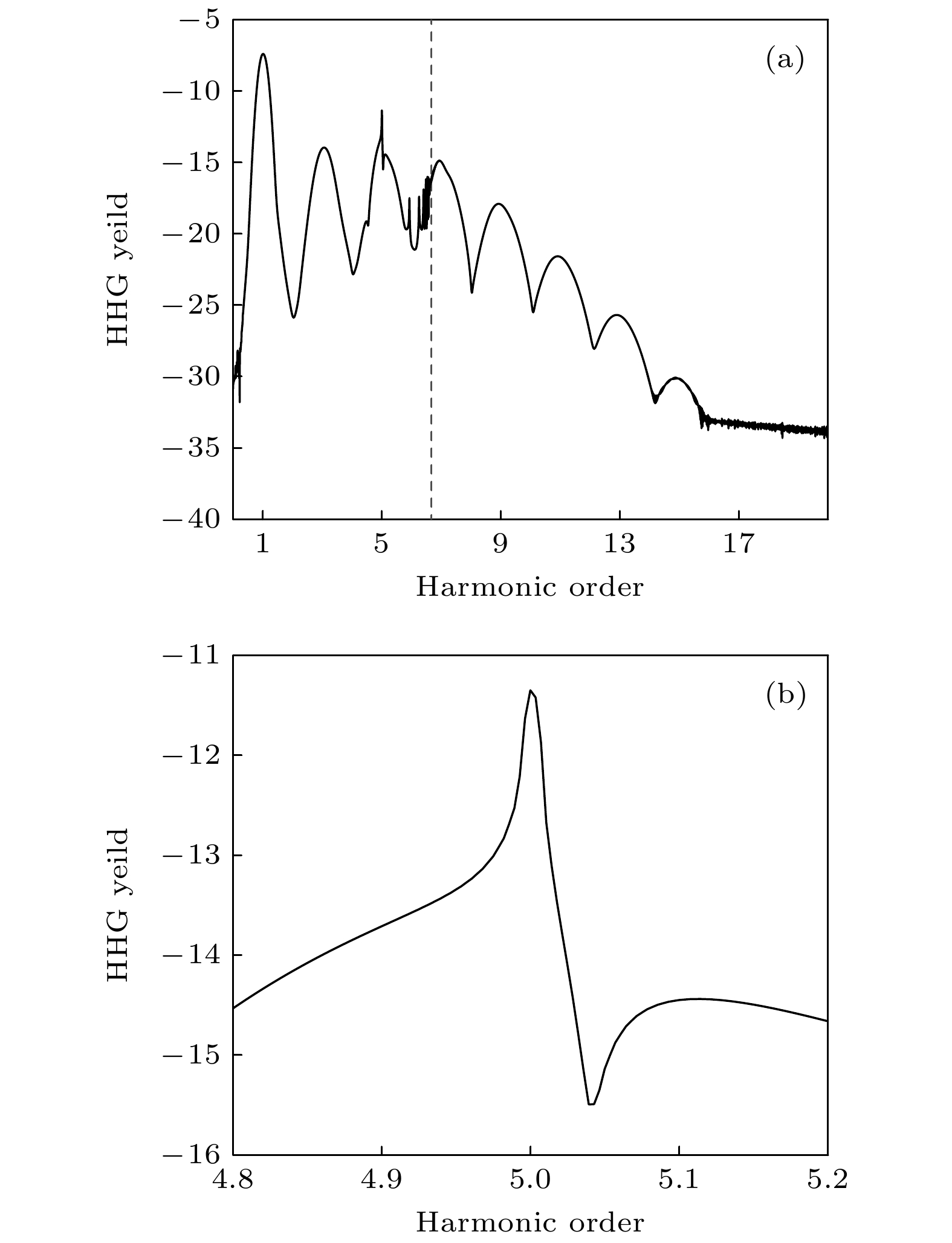
图 1 (a) 计算得到的高次谐波谱. 虚线标记了阈上和阈下谐波能量的分界点. (b) 为图(a)中第五次谐波的局部放大图. 激光波长为608 nm, 强度为5 × 1012 W cm–2
Fig. 1. (a) Calculated high-harmonic spectrum. The dashed line marks the boundary between above-threshold and below-threshold harmonic energies. (b) Partial enlarged view of the fifth harmonic in Fig. (a). The laser wavelength is 608 nm with an intensity of 5 × 1012 W cm–2.
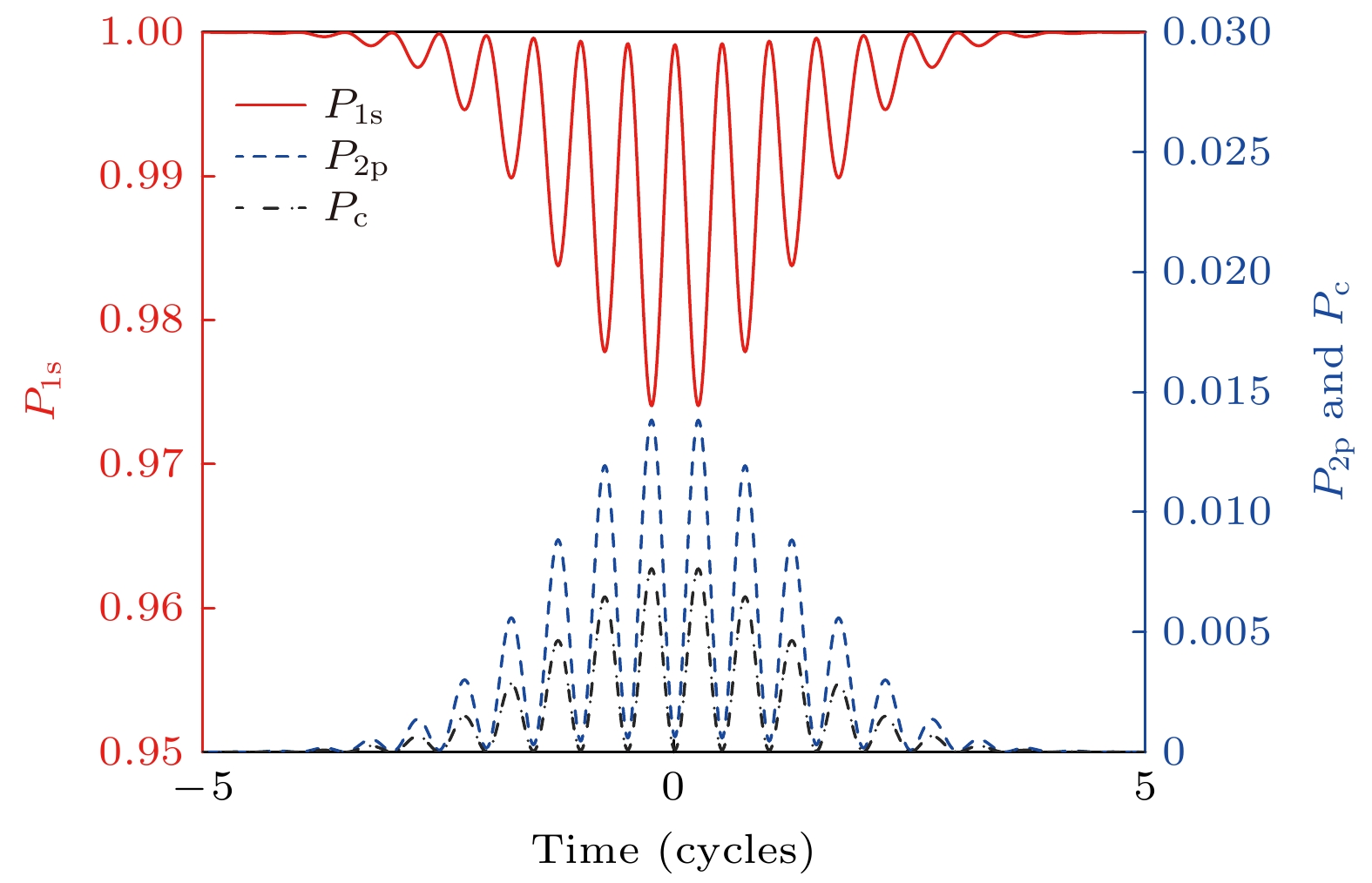
图 2 双纵轴图: 随时间演化的态概率. 左轴为基态$ \left |1 s \right \rangle $, 右轴为激发态$ \left | 2 p \right \rangle $与连续态$ \left | c \right \rangle $的概率分布
Fig. 2. Dual-axis plot: Time evolution of state probabilities. The left axis corresponds to the ground state $ \left |1 s \right \rangle $, and the right axis shows the probabilities of the excited state $ \left | 2 p \right \rangle $ and continuum state $ \left | c \right \rangle $.
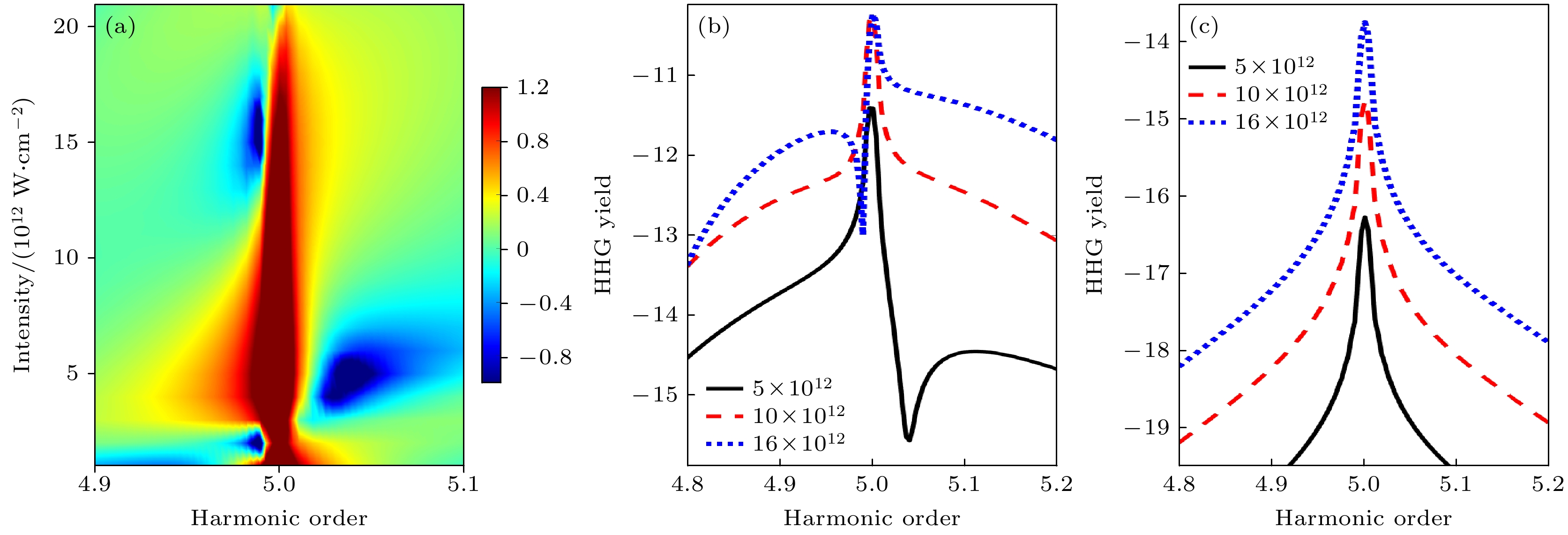
图 3 (a) 归一化的第五次谐波强度随激光强度变化的谱图, 激光强度从1012 W cm–2扫描至2 × 1013 W cm–2; (b) 对应三种典型强度(黑: 5 × 1012 W cm–2, 红: 1013 W cm–2, 蓝: 1.6 × 1013 W cm–2)下的谱线形; (c) 使用简化二能级模型所得结果, 仅包含$ \left | 1 s \right \rangle - $$ \left | 2 p \right \rangle $偶极路径
Fig. 3. (a) Spectral map of normalized fifth harmonic intensity versus laser intensity scanned from 1012 W cm–2 to 2 × 1013 W cm–2. (b) Spectral line shapes at three representative intensities (black: 5 × 1012 W cm–2, red: 1013 W cm–2, blue: 1.6 × 1013 W cm–2). (c) Results obtained using a simplified two-level model considering only the dipole $ \left | 1 s \right \rangle - \left | 2 p \right \rangle $ transition pathway.
-
[1] Fano U 1961 Phys. Rev. 124 1866
Google Scholar
[2] Kobayashi K, Aikawa H, Katsumoto S, Iye Y 2002 Phys. Rev. Lett. 88 256806
Google Scholar
[3] Wang Y, Liao L, Hu T, Luo S, Wu L, Wang J, Zhang Z, Xie W, Sun L, Kavokin A V, Shen X, Chen Z 2017 Phys. Rev. Lett. 118 063602
Google Scholar
[4] Karmakar S, Kumar D, Varshney R K, Chowdhury D R 2020 Opt. Lett. 45 3386
Google Scholar
[5] Ott C, Aufleger L, Ding T, Rebholz M, Magunia A, Hartmann M, Stooß V, Wachs D, Birk P, Borisova G D, Meyer K, Rupprecht P, da Costa Castanheira C, Moshammer R, Attar A R, Gaumnitz T, Loh Z H, Düsterer S, Treusch R, Ullrich J, Jiang Y, Meyer M, Lambropoulos P, Pfeifer T 2019 Phys. Rev. Lett. 123 163201
Google Scholar
[6] Fasshauer E, Madsen L B 2020 Phys. Rev. A 101 043414
Google Scholar
[7] Wickenhauser M, Burgdörfer J, Krausz F, Drescher M 2005 Phys. Rev. Lett. 94 023002
Google Scholar
[8] Themelis S I, Lambropoulos P, Meyer M 2004 Journal of Physics B: Atomic, Molecular and Optical Physics 37 4281
Google Scholar
[9] Tong X M, Lin C D 2005 Phys. Rev. A 71 033406
Google Scholar
[10] Zhao Z X, Lin C D 2005 Phys. Rev. A 71 060702
Google Scholar
[11] Wang H, Chini M, Chen S, Zhang C H, He F, Cheng Y, Wu Y, Thumm U, Chang Z 2010 Phys. Rev. Lett. 105 143002
Google Scholar
[12] Kaldun A, Ott C, Blättermann A, Laux M, Meyer K, Ding T, Fischer A, Pfeifer T 2014 Phys. Rev. Lett. 112 103001
Google Scholar
[13] Kaldun A, Blättermann A, Stooß V, Donsa S, Wei H, Pazourek R, Nagele S, Ott C, Lin C D, Burgdörfer J, Pfeifer T 2016 Science 354 738
Google Scholar
[14] Peng P, Marceau C, Hervé M, Corkum P B, Naumov A Y, Villeneuve D M 2019 Nature Communications 10 5269
Google Scholar
[15] Veit S, Paul B, Alexander B, Maximilian H, D B G, Christian O, Thomas P 2020 Phys. Rev. Res. 2 032041
Google Scholar
[16] Harkema N, Cariker C, Lindroth E, Argenti L, Sandhu A 2021 Phys. Rev. Lett. 127 023202
Google Scholar
[17] Peng P, Yonghao M, Marianna L, Mathew B, Xiaoyan D, Yu N A, B C P, M V D 2022 Nature Photonics 16 4551
[18] Serov V V, Kheifets A S 2024 Phys. Rev. A 110 043107
Google Scholar
[19] Han M, Liang H, Ji J B, Sum L C, Ueda K, Rost J M, Wörner H J 2025 Ultrafast Science 5 0091
Google Scholar
[20] Lewenstein M, Balcou P, Ivanov M Y, L'Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[21] Soifer H, Botheron P, Shafir D, Diner A, Raz O, Bruner B D, Mairesse Y, Pons B, Dudovich N 2010 Phys. Rev. Lett. 105 143904
Google Scholar
[22] C Y D, R S T, Jun Y, L T J, James H, B G M, J S K 2009 Nature Physics 5 815820
[23] Hostetter J A, Tate J L, Schafer K J, Gaarde M B 2010 Phys. Rev. A 82 023401
Google Scholar
[24] Xiong W H, Geng J W, Tang J Y, Peng L Y, Gong Q 2014 Phys. Rev. Lett. 112 233001
Google Scholar
[25] Xiong W H, Jin J Z, Peng L Y, Gong Q 2017 Phys. Rev. A 96 023418
Google Scholar
[26] Camp S, Schafer K J, Gaarde M B 2015 Phys. Rev. A 92 013404
Google Scholar
[27] Peng-Cheng L, Yae-Lin S, Cecil L, Shih-I C 2015 Nature Communications 6 7178
Google Scholar
[28] Chu W C, Travers J C, Russell P S J 2016 New Journal of Physics 18 023018
Google Scholar
[29] Beaulieu S, Camp S, Descamps D, Comby A, Wanie V, Petit S, Légaré F, Schafer K J, Gaarde M B, Catoire F, Mairesse Y 2016 Phys. Rev. Lett. 117 203001
Google Scholar
[30] Du L L, Wang G L, Li P C, Zhou X X, Zhao Z X 2018 Phys. Rev. A 97 023404
Google Scholar
[31] Guo Q L, Li P C, Zhou X X, Chu S I 2018 Optics Communications 410 262
Google Scholar
[32] Wang B, Zhang Y, Lan P, Zhai C, Li M, Zhu X, Chen J, Lu P, Lin C D 2021 Phys. Rev. A 103 053119
Google Scholar
[33] Jun P T, C L J 1986 The Journal of Chemical Physics 85 5870
Google Scholar
[34] Burnett K, Reed V C, Cooper J, Knight P L 1992 Phys. Rev. A 45 3347
Google Scholar
[35] Sundaram B, Milonni P W 1990 Phys. Rev. A 41 6571
Google Scholar
[36] Figueira de Morisson Faria C, Dörr M, Sandner W 1998 Phys. Rev. A 58 2990
Google Scholar
[37] Figueira de Morisson Faria C, Rotter I 2002 Phys. Rev. A 66 013402
Google Scholar
[38] Bickel W S, Goodman A S 1966 Phys. Rev. 148 1
Google Scholar
[39] Bo L, Rujiang L, Jiahui F, Qun W, Kuang Z, Wan C, Zhefei W, Ruyu M 2016 Scientific Reports 6 31884
Google Scholar
[40] Iizawa M, Kosugi S, Koike F, Azuma Y 2021 Physica Scripta 96 055401
Google Scholar
下载:
计量
- 文章访问数: 223
- PDF下载量: 10
- 被引次数: 0
