-
人工局域表面等离激元结构具有许多特殊的光学性质, 对于新一代光学元件的设计具有重要的意义. 本文设计了一种在硅盘中周期性嵌入金属条的结构, 从而使得物体在任意方向的光散射均被抑制, 实现了全方向隐身的效果. 通过理论分析与数值模拟, 发现这种空心的人工局域表面等离激元结构在一定频率下会出现强散射抑制现象, 这是由结构的散射波与背景波之间干涉相消产生的效果, 且由于结构是一种周期性环状结构, 因此可以在散射抑制的频率点下实现全方向的隐身效果. 这为分析人工局域表面等离激元结构的物理隐身和光学响应提供了一条新的途径. 此外, 本文还分析了结构在不同参数条件下对散射谱移动规律的影响. 本文的结果适用于微波到太赫兹波区域, 可以应用于各种先进的光学器件, 如雷达、隐身涂层、传感器和探测器等.
-
关键词:
- 人工局域表面等离激元 /
- 超构材料 /
- 结构散射 /
- 全向隐身
Surface plasmons include surface plasmon polaritons and localized surface plasmons, which are electromagnetic wave confined at the interface of the metal and dielectric. Spoof surface plasmonic structure has many special optical properties, which is of great significance for designing new-generation optical elements. In order to transfer the features of the surface plasmon polaritons and localized surface plasmons to microwave-terahertz region, Pendry et al. (Pendry J B, Martin-Moreno L, Garcia-Vidal F J 2004 Science 305 847) have proposed the spoof surface plasmon polaritons based on a metal structure with grooved stripes. In this paper, a hollow textured perfect electric conductor cylinder with periodic cut-through slits structure is designed to suppress the light scattering of the object in any direction and achieve the effect of omnidirectional cloaking while the transverse magnetic polarization wave propagates along the x direction. And the locations of the electrical and magnetic modes can be freely modulated by tailoring the structural geometric construction. In order to find the physical mechanism behind the abnormal phenomenon, through theoretical analysis and numerical simulation, we find that the strong scattering suppression of this spoof surface plasmonic polariton structure is caused by the interference between the background wave and Mie scattering of the structural unit, and it can be equivalent to a ring metamaterial due to the special structural design, in order to achieve the omnidirectional cloaking. It implies that we can hide objects in metal strips due to the fact that the metal in the microwave-to-terahertz region is equivalent to a perfect electrical conductor. This opens up a new way to analyzing the physical cloaking and optical response of spoof surface plasmonic polaritons structure. In addition, we also analyze the influence of the structure on the movement law of the scattering spectrum under different structural parameters. This enables us to have an in-depth understanding of the influence of structural parameters on the structural scattering spectrum. Our results can be applied to the microwave-to-terahertz region and a variety of advanced optic devices such as radars, cloaking coatings, sensors and detectors.-
Keywords:
- spoof surface plasmonic polaritons /
- metamaterial /
- structural scattering /
- omnidirectional cloaking
[1] Zheludev N I, Kivshar Y S 2012 Nat. Mater. 11 917
Google Scholar
[2] Cummer S. A, Popa B, Schuring D, Smith D. R, Pendry J 2006 Phys. Rev. E 74 036621
Google Scholar
[3] Cai W, Chettiar U K, Kildishev A V, Shalaev V M 2007 Nat. Photon. 1 224
Google Scholar
[4] Zhang S, Genov D A, Sun C, Zhang X 2008 Phys. Rev. Lett. 100 123002
Google Scholar
[5] Monticone F, Argyropoulos C, Alù A 2013 Phys. Rev. Lett. 110 113901
Google Scholar
[6] Kort-Kamp W J M, Rosa F S S, Pinheiro F A, Farina C 2013 Phys. Rev. Lett. 111 215504
Google Scholar
[7] Leonhardt U, Philbin T G 2006 New J. Phys. 8 247
Google Scholar
[8] Chen P Y, Soric J, Alù A 2012 Adv. Mater. 24 OP281
[9] Pendry J B, Schuring D, Simith D R 2006 Science 312 1780
Google Scholar
[10] Schuring D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F, Smith D R 2006 Science 314 977
[11] Liu R, Ji C, Mock J J, Chin J Y, Cui T J, Smith D R 2009 Science 323 366
Google Scholar
[12] Zharova N A, Shadriviv I V, Zharov A A, Kivshar Y S 2012 Opt. Express 20 14954
Google Scholar
[13] Stockman M I 2004 Phys. Rev. Lett. 93 137404
Google Scholar
[14] Prodan E, Radloff C, Halas N J, Nordlander P 2003 Science 302 419
Google Scholar
[15] Anker J N, Hall W P, Lyandres O, Shah N, Zhao J, Duyne R P V 2008 Nat. Mater. 7 442
Google Scholar
[16] Pors A, Moreno E, Martin-Moreno L, Pendry J B, Garcia-Vidal F J 2012 Phys. Rev. Lett. 108 223905
Google Scholar
[17] Sheng X P, Cui T J 2014 Laser Photon. Rev. 8 137
Google Scholar
[18] Gao Z, Gao F, Xu H, Zhang Y, Zhang B L 2016 Opt. Lett. 41 2181
Google Scholar
[19] Alù A, Engheta N 2009 Phys. Rev. Lett. 102 233901
Google Scholar
[20] Wu H W, Chen H J, Fan H Y, Li Y, Fang X W 2017 Opt. Lett. 42 791
Google Scholar
[21] 李梦君, 方晖, 李小明, 袁小聪 2016 65 057302
Google Scholar
Li M J, Fang H, Li X M, Yuan X C 2016 Acta Phys. Sin. 65 057302
Google Scholar
[22] 高东宝, 曾新吾 2012 61 184301
Google Scholar
Gao D B, Zeng X W 2012 Acta Phys. Sin. 61 184301
Google Scholar
[23] 汪会波, 罗孝阳, 董建峰 2015 64 154102
Google Scholar
Wang H B, Luo X Y, Dong J F 2015 Acta Phys. Sin. 64 154102
Google Scholar
[24] 王超, 李勇峰, 沈杨, 丰茂昌, 王甲富, 马华, 张介秋, 屈绍波 2018 67 204101
Google Scholar
Wang C, Li Y F, Shen Y, Feng M C, Wang J F, Ma H, Zhang J Q, Qu S B 2018 Acta Phys. Sin. 67 204101
Google Scholar
[25] Wu H W, Han Y Z, Chen H J, Zhou Y, Li X C, Gao J, Sheng Z Q 2017 Opt. Lett. 42 4521
Google Scholar
[26] Wu H W, Chen H J, Xu H F, Fan R H, Li Y 2018 Sci. Rep. 8 8817
Google Scholar
[27] Wu H W, Li Yang, Chen H J, Sheng Z Q, Jing H, Fan R H, Peng R W 2019 Appl. Nano Mater. 2 1045
Google Scholar
[28] Rybin M V, Samusev K B, Sinev I S, Semouchkin G, Semouchkina E, Kivshar Y S, Limonov M F 2013 Opt. Express 21 30107
Google Scholar
[29] Fano U 1961 Phys. Rev. 124 1866
Google Scholar
[30] Limonov M F, Rybin M V, Poddubny A N, Kivshar Y S 2017 Nat. Photon. 11 543
Google Scholar
[31] Liu X, Zhao Q, Lan C, Zhou J 2013 Appl. Phys. Lett. 103 031910
Google Scholar
[32] Wu H W, Wang F, Dong Y Q, Shu F Z, Zhang K, Peng R W, Xiong X, Wang M 2015 Opt. Express 23 32087
Google Scholar
[33] van de Hulst H C 1957 Light Scattering: by Small Particles (New York: Courier Dover Publications) p23
[34] Bohren C F, Huffman D R 1998 Absorption and Scattering of Light by Small Particles (New York: Wiley-VCH) p40
[35] Stratton J A 2007 Electromagnetic Theory (New York: Wiley) p67
[36] Rybin M V, Samusev K B, Kapitanova P V, Filonov D S, Belov P A, Kivshar Y S, Limonov M F 2017 Phys. Rev. B 95 165119
Google Scholar
[37] Fu T, Gao X, Xiao G L, Sun T Y, Li Q, Zhang F B, Chen Y H, Li H O, Deng Z L 2019 Opt. Mater. Express 9 944
Google Scholar
[38] Deng Z L, Li X P, Fu T, Wang G P 2017 IEEE Photon. J. 9 4801107
[39] Deng Z L, Yogesh N, Chen X D, Chen W J, Dong J W, Ouyang Z B, Wang G P 2015 Sci. Rep. 5 18461
-
图 1 (a)人工局域等离激元的结构设计; (b)放大结构的基本构成模块; (c)等效的超构材料; (d)超构材料空间介电常数分布; (e)磁导率的空间分布
Fig. 1. (a) Structural design of spoof localized surface plasmonic; (b) the basic building blocks of the amplifier structure; (c) equivalent metamaterial; (d) spatial dielectric constant distribution of metamaterial; (e) the spatial distribution of permeability.
图 2 (a)计算的空心人工局域表面等离激元结构的散射谱, 其中浅蓝色区域代表低阶模式, 砖红色区域代表高阶模式; (b)−(d)低阶模式区域中三个共振峰的场分布, 分别对应于磁偶极模式、电偶极模式和电四极模式
Fig. 2. (a) Calculated scattering cross section spectrum for the textured perfect electric conductor hollow cylinder. The light blue and brick red area represent the lower and higher order mode, respectively. (b)−(d) The field distribution of three resonant peaks in the lower mode region correspond to magnetic dipole mode, electric dipole mode and electric quadrupole mode.
图 3 计算的形变的具有完美电导体纹理的空心硅盘结构的散射谱 (a)改变内半径从0.1 m至0.2 m; (b)改变外半径从0.6 m至0.7 m; (c)裂缝a和周期d的比值从0.2至0.4; (d)电介质折射率大小从3改变至5
Fig. 3. Calculated scattering cross section of the textured perfect electric conductor hollow cylinder for changing: (a) Changing the inner radius from 0.1 m to 0.2 m; (b) outer radius from 0.6 m to 0.7 m; (c) the rations between the width of slit a and period d from a/d = 0.2 to a/d = 0.4; (d) the refractive index of the dielectric from n = 3 to n = 5.
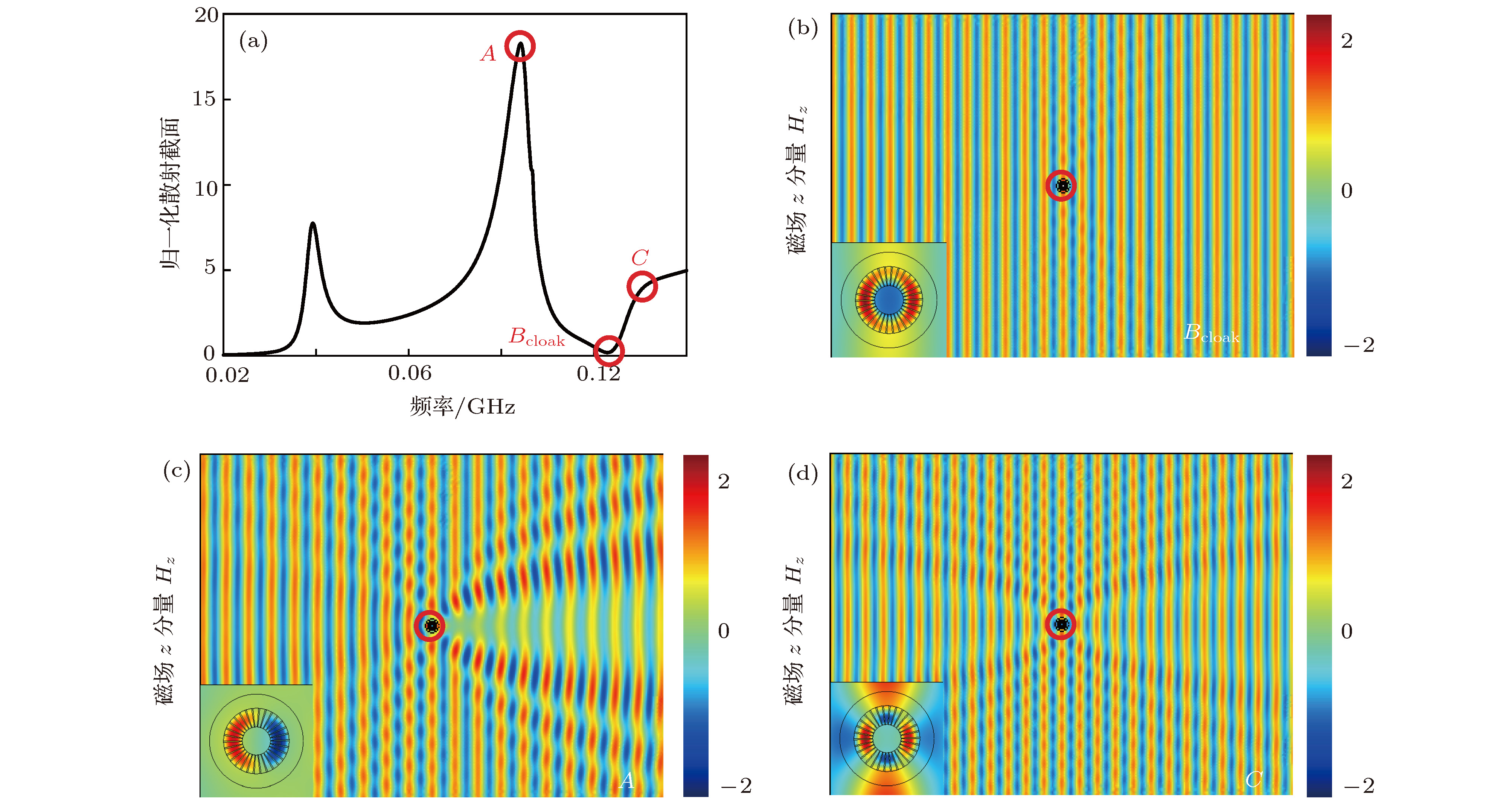
图 4 (a)计算的r = 0.3, R = 0.7时具有完美电导体纹理的空心硅盘结构的散射谱; (b)在B位置时的场分布图, (c)和(d)分别对应着A点和C点的场分布图, 图中内嵌的图为红色圆圈内结构的放大
Fig. 4. (a) Calculated scattering cross section of the textured perfect electric conductor hollow cylinder at r = 0.3 m and R = 0.7 m; (b) field distribution at position B, (c) and (d) correspond to the field distribution of point A and point C respectively, the figure embedded in (b)−(d) shows the enlargement of the structure in the red circle.
-
[1] Zheludev N I, Kivshar Y S 2012 Nat. Mater. 11 917
Google Scholar
[2] Cummer S. A, Popa B, Schuring D, Smith D. R, Pendry J 2006 Phys. Rev. E 74 036621
Google Scholar
[3] Cai W, Chettiar U K, Kildishev A V, Shalaev V M 2007 Nat. Photon. 1 224
Google Scholar
[4] Zhang S, Genov D A, Sun C, Zhang X 2008 Phys. Rev. Lett. 100 123002
Google Scholar
[5] Monticone F, Argyropoulos C, Alù A 2013 Phys. Rev. Lett. 110 113901
Google Scholar
[6] Kort-Kamp W J M, Rosa F S S, Pinheiro F A, Farina C 2013 Phys. Rev. Lett. 111 215504
Google Scholar
[7] Leonhardt U, Philbin T G 2006 New J. Phys. 8 247
Google Scholar
[8] Chen P Y, Soric J, Alù A 2012 Adv. Mater. 24 OP281
[9] Pendry J B, Schuring D, Simith D R 2006 Science 312 1780
Google Scholar
[10] Schuring D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F, Smith D R 2006 Science 314 977
[11] Liu R, Ji C, Mock J J, Chin J Y, Cui T J, Smith D R 2009 Science 323 366
Google Scholar
[12] Zharova N A, Shadriviv I V, Zharov A A, Kivshar Y S 2012 Opt. Express 20 14954
Google Scholar
[13] Stockman M I 2004 Phys. Rev. Lett. 93 137404
Google Scholar
[14] Prodan E, Radloff C, Halas N J, Nordlander P 2003 Science 302 419
Google Scholar
[15] Anker J N, Hall W P, Lyandres O, Shah N, Zhao J, Duyne R P V 2008 Nat. Mater. 7 442
Google Scholar
[16] Pors A, Moreno E, Martin-Moreno L, Pendry J B, Garcia-Vidal F J 2012 Phys. Rev. Lett. 108 223905
Google Scholar
[17] Sheng X P, Cui T J 2014 Laser Photon. Rev. 8 137
Google Scholar
[18] Gao Z, Gao F, Xu H, Zhang Y, Zhang B L 2016 Opt. Lett. 41 2181
Google Scholar
[19] Alù A, Engheta N 2009 Phys. Rev. Lett. 102 233901
Google Scholar
[20] Wu H W, Chen H J, Fan H Y, Li Y, Fang X W 2017 Opt. Lett. 42 791
Google Scholar
[21] 李梦君, 方晖, 李小明, 袁小聪 2016 65 057302
Google Scholar
Li M J, Fang H, Li X M, Yuan X C 2016 Acta Phys. Sin. 65 057302
Google Scholar
[22] 高东宝, 曾新吾 2012 61 184301
Google Scholar
Gao D B, Zeng X W 2012 Acta Phys. Sin. 61 184301
Google Scholar
[23] 汪会波, 罗孝阳, 董建峰 2015 64 154102
Google Scholar
Wang H B, Luo X Y, Dong J F 2015 Acta Phys. Sin. 64 154102
Google Scholar
[24] 王超, 李勇峰, 沈杨, 丰茂昌, 王甲富, 马华, 张介秋, 屈绍波 2018 67 204101
Google Scholar
Wang C, Li Y F, Shen Y, Feng M C, Wang J F, Ma H, Zhang J Q, Qu S B 2018 Acta Phys. Sin. 67 204101
Google Scholar
[25] Wu H W, Han Y Z, Chen H J, Zhou Y, Li X C, Gao J, Sheng Z Q 2017 Opt. Lett. 42 4521
Google Scholar
[26] Wu H W, Chen H J, Xu H F, Fan R H, Li Y 2018 Sci. Rep. 8 8817
Google Scholar
[27] Wu H W, Li Yang, Chen H J, Sheng Z Q, Jing H, Fan R H, Peng R W 2019 Appl. Nano Mater. 2 1045
Google Scholar
[28] Rybin M V, Samusev K B, Sinev I S, Semouchkin G, Semouchkina E, Kivshar Y S, Limonov M F 2013 Opt. Express 21 30107
Google Scholar
[29] Fano U 1961 Phys. Rev. 124 1866
Google Scholar
[30] Limonov M F, Rybin M V, Poddubny A N, Kivshar Y S 2017 Nat. Photon. 11 543
Google Scholar
[31] Liu X, Zhao Q, Lan C, Zhou J 2013 Appl. Phys. Lett. 103 031910
Google Scholar
[32] Wu H W, Wang F, Dong Y Q, Shu F Z, Zhang K, Peng R W, Xiong X, Wang M 2015 Opt. Express 23 32087
Google Scholar
[33] van de Hulst H C 1957 Light Scattering: by Small Particles (New York: Courier Dover Publications) p23
[34] Bohren C F, Huffman D R 1998 Absorption and Scattering of Light by Small Particles (New York: Wiley-VCH) p40
[35] Stratton J A 2007 Electromagnetic Theory (New York: Wiley) p67
[36] Rybin M V, Samusev K B, Kapitanova P V, Filonov D S, Belov P A, Kivshar Y S, Limonov M F 2017 Phys. Rev. B 95 165119
Google Scholar
[37] Fu T, Gao X, Xiao G L, Sun T Y, Li Q, Zhang F B, Chen Y H, Li H O, Deng Z L 2019 Opt. Mater. Express 9 944
Google Scholar
[38] Deng Z L, Li X P, Fu T, Wang G P 2017 IEEE Photon. J. 9 4801107
[39] Deng Z L, Yogesh N, Chen X D, Chen W J, Dong J W, Ouyang Z B, Wang G P 2015 Sci. Rep. 5 18461
下载:
计量
- 文章访问数: 9651
- PDF下载量: 180
- 被引次数: 0
