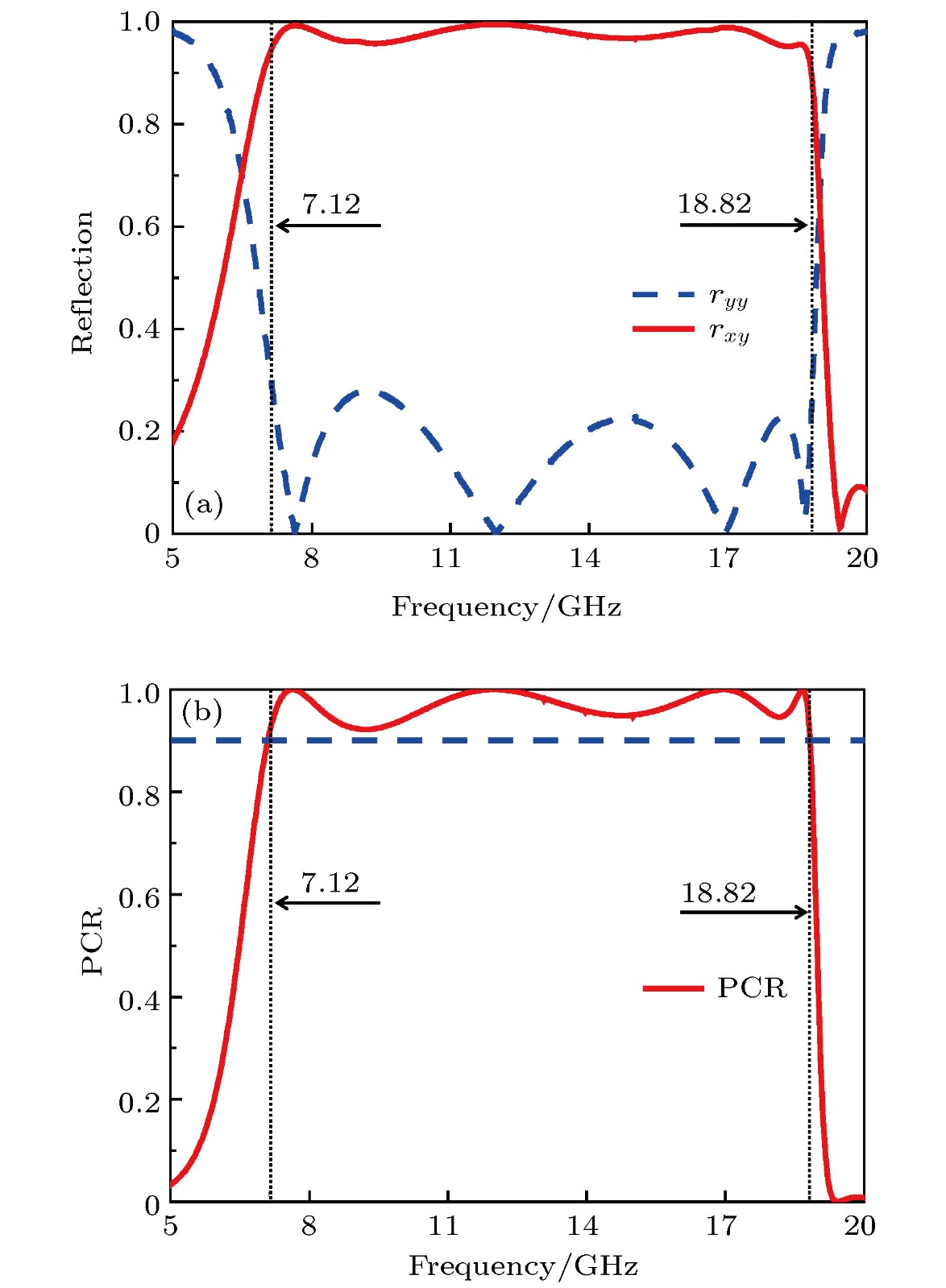
-
电磁波的极化调控在卫星通信、雷达探测以及立体显示成像等领域有重要的应用价值, 探索易于加工、转换效率高、工作频带宽的高性能极化转换器具有重要的研究意义. 本文提出了一种基于方形开口环超构表面的线性极化转换器, 该转换器具有各向异性特点, 反射电场沿两个对角线方向的分量振幅相等, 相位相差180°, 导致在反射模式下能够将入射波的极化方向旋转90°. 实验测试结果表明, 在7.12—18.82 GHz频带范围内极化转换率高于90%, 相对带宽达到90%. 频带的显著拓宽基于四个谐振频点, 每个谐振频点的转换效率都接近100%. 实验结果与模拟结果相符合, 验证了提出的超构表面可以在较宽的频带范围内实现电磁波的90°极化旋转.
Polarization state of electromagnetic wave has important applications in satellite communication, radar detection, and stereoscopic display imaging. Therefore, the control of polarization state of electromagnetic wave is an important direction in scientific research. The traditional method of manipulating the polarization state is mainly realized based on Faraday effect and birefringent crystal, which has a certain requirement for the material thickness (leading to large volume), and does not have broadband characteristics (leading to narrow band). Recently, metamaterial with subwavelength meta-atoms, has achieved many exotic phenomena and functionalities that cannot be found in nature. As an important branch of metamaterial-based devices, polarization converter has attracted great attention and achieved significant progress. However, most of them cannot realize ultra-broadband, high-efficiency, wide-angle, and simple geometry simultaneously. In this paper, a linear polarization converter based on a square split ring metasurface is proposed. Due to the anisotropic structure, the amplitudes of the reflected electric field along the two diagonal lines are equal, and their phase difference is 180°. As a result, the polarization direction of the incident wave can be rotated 90°. The simulation results show that the polarization conversion ratio (PCR) is higher than 90% in a frequency range from 7.12 to 18.82 GHz, which means that the relative bandwidth reaches 90%. The significant bandwidth expansion is attributed to the four electromagnetic resonances generated in a square-split-ring unit. We investigate the influence of geometric parameters on PCR in detail. We also examine the performance of the proposed structure under oblique incidence. It has little effect on the co-polarization and cross-polarization reflection coefficients when the incident angle is changed from 0° to 45°. Even if the incident angle reaches 45°, the mean PCR remains above 80%. The PCRs of the four electromagnetic resonant points are all close to 100%. Finally, we fabricate and measure the proposed polarization converter that contains $30\times30$ unit cells. The experimental results are in good agreement with the simulation results, and thus validating the design.In conclusion, we propose both theoretically and experimentally a linear polarization converter that possesses ultra-broadband, high-efficiency, wide-angle, and simple geometry simultaneously. The proposed scheme can be extended to terahertz and even optical frequencies. -
Keywords:
- polarization converter /
- metamaterials /
- metasurface /
- ultra-broadband /
- anisotropy
[1] Beruete M, Navarro-Cia M, Sorolla M, Campillo I 2008 J. Appl. Phys. 103 053102
Google Scholar
[2] Xu J, Li T, Lu F F, Wang S M, Zhu S N 2011 Opt. Express 19 748
Google Scholar
[3] Shi H J, Ma H F, Jiang W X, Cui T J 2012 Phys. Rev. B 86 035103
Google Scholar
[4] Smith D R, Pendry J B, Wiltshire M C K 2004 Science 305 788
Google Scholar
[5] Lee H, Xiong Y, Fang N, Srituravanich W, Durant S, Ambati M, Sun C, Zhang X 2005 New J. Phys. 7 255
Google Scholar
[6] Schurig D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F, Smith D R 2006 Science 314 977
Google Scholar
[7] Landy N I, Sajuyigbe S, Mock J J, Smith D R, Padilla W J 2008 Phys. Rev. Lett. 100 207402
Google Scholar
[8] Ye Y, He S 2010 Appl. Phys. Lett. 96 203501
Google Scholar
[9] Menzel C, Helgert C, Rockstuhl C, Kley E B, Tunnermann A, Pertsch T, Lederer F 2010 Phys. Rev. Lett. 104 253902
Google Scholar
[10] Shi H, Zhang A, Zheng S, Li J, Jiang Y 2014 Appl. Phys. Lett. 104 034102
Google Scholar
[11] Wang S, Liu W, Wen G 2018 Sci. Rep. 8 3791
Google Scholar
[12] Hao J, Yuan Y, Ran L, Jiang T, Kong J, Chan C T, Zhou L 2007 Phys. Rev. Lett. 99 063908
Google Scholar
[13] Feng M, Wang J, Ma H, Mo W, Ye H, Qu S 2013 J. Appl. Phys. 114 074508
Google Scholar
[14] Pu M, Chen P, Wang Y, Zhao Z, Huang C, Wang C, Ma X, Luo X 2013 Appl. Phys. Lett. 102 131906
Google Scholar
[15] Cheng Y Z, Withayachumnankul W, Upadhyay A, Headland D, Nie Y, Gong R Z, Bhaskaran M, Sriram S, Abbott D 2014 Appl. Phys. Lett. 105 181111
Google Scholar
[16] Zhang L, Zhou P, Chen H, Lu H, Xie J, Deng L 2015 Appl. Phys. B 120 617
Google Scholar
[17] Chen H, Wang J, Ma H, Qu S, Xu Z, Zhang A, Yan M, Li Y 2014 J. Appl. Phys. 115 154504
Google Scholar
[18] Ding J, Arigong B, Ren H, Zhou M, Shao J, Lin Y, Zhang H 2014 Opt. Express 22 29143
Google Scholar
[19] Shi H, Li J, Zhang A, Wang J, Xu Z 2014 Opt. Express 22 20973
Google Scholar
[20] Wen X, Zheng J 2014 Opt. Express 22 28292
Google Scholar
[21] 范亚, 屈绍波, 王甲富, 张介秋, 冯明德, 张安学 2015 64 184101
Google Scholar
Fan Y, Qu S B, Wang J F, Zhang J Q, Feng M D, Zhang A X 2015 Acta Phys. Sin. 64 184101
Google Scholar
[22] Gao X, Han X, Cao W, Li H, Ma H, Cui T 2015 IEEE Trans. Antennas Propag. 63 3522
Google Scholar
[23] Zhao J, Cheng Y 2017 Optik 136 52
Google Scholar
[24] 余积宝, 马华, 王甲富, 冯明德, 李勇峰, 屈绍波 2015 64 178101
Google Scholar
Yu J B, Ma H, Wang J F, Feng M D, Li Y F, Qu S B 2015 Acta Phys. Sin. 64 178101
Google Scholar
[25] Zhao J, Cheng Y 2016 Appl. Phys. B 122 255
[26] Ding F, Wang Z, He S, Shalaev V M, Kildishev A V 2015 ACS Nano 9 4111
Google Scholar
[27] Zhang L, Zhou P, Chen H, Lu H, Xie H, Zhang L, Li E, Xie J, Deng L 2016 Sci. Rep. 6 33826
Google Scholar
[28] Zhang L, Zhou P, Lu H, Zhang L, Xie J, Deng L 2016 Opt. Mater. Express 6 1393
Google Scholar
[29] Mei Z, Ma X, Lu C, Zhao Y 2017 AIP Adv. 7 125323
Google Scholar
[30] 方振华, 罗春荣, 赵晓鹏 2017 光子学报 46 1216001
Fang Z H, Luo C R, Zhao X P 2017 Acta Photon. Sin. 46 1216001
[31] Khan M I, Fraz Q, Tahir F A 2017 J. Appl. Phys. 121 045103
Google Scholar
[32] Li S, Cao X, Xu L, Zhou L, Yang H, Han J, Zhang Z, Zhang D, Liu X, Zhang C, Zheng Y, Zhao Y 2016 Sci. Rep. 5 37409
[33] Sui S, Ma H, Wang J, Feng M, Pang Y, Xia S, Xu Z, Qu S 2016 Appl. Phys. Lett. 109 014104
Google Scholar
[34] 韩江枫, 曹祥玉, 高军, 李思佳, 张晨 2016 65 044201
Google Scholar
Han J F, Cao X Y, Gao J, Li S J, Zhang C 2016 Acta Phys. Sin. 65 044201
Google Scholar
[35] Jia Y, Liu Y, Zhang W, Gong S 2016 Appl. Phys. Lett. 109 051901
Google Scholar
-
图 1 基本单元结构示意图 (a) 立体图; (b) 俯视图
Fig. 1. Schematic demonstration of the unit cell: (a) 3D view; (b) top view.
图 2 (a) 极化转换器的工作原理; (b) 反射波沿u和v方向的振幅及相位差
Fig. 2. (a) The working principle of the proposed polarization converter; (b) amplitudes and phase difference of reflected wave along u and v directions.
图 3 (a) 交叉极化和共极化反射系数; (b) 极化转换率
Fig. 3. (a) Reflection coefficients of cross-polarization and co-polarization; (b) polarization conversion ratio.
图 4 上下金属表面的电流分布 (a) 7.64 GHz; (b) 16.94 GHz
Fig. 4. Distributions of the surface current on the metallic surfaces: (a) 7.64 GHz; (b) 16.94 GHz.
图 5 (a) 共极化反射谱; (b) 交叉极化反射谱; (c) 平均极化转换效率随入射角的变化
Fig. 5. (a) Reflection spectra for co-polarization; (b) reflection spectra for cross-polarization; (c) mean PCR with the change of incident angle.
图 6 不同的结构参数对极化转换器的性能的影响
Fig. 6. Influence of different geometric parameters on the performance of polarization converter.
图 7 (a) 加工样品与测试系统; (b) rxy测试结果与仿真结果; (c) ryy测试结果与仿真结果
Fig. 7. (a) Fabricated sample and measurement system; (b) measured result and simulation result of rxy; (c) measured result and simulation result of ryy.
-
[1] Beruete M, Navarro-Cia M, Sorolla M, Campillo I 2008 J. Appl. Phys. 103 053102
Google Scholar
[2] Xu J, Li T, Lu F F, Wang S M, Zhu S N 2011 Opt. Express 19 748
Google Scholar
[3] Shi H J, Ma H F, Jiang W X, Cui T J 2012 Phys. Rev. B 86 035103
Google Scholar
[4] Smith D R, Pendry J B, Wiltshire M C K 2004 Science 305 788
Google Scholar
[5] Lee H, Xiong Y, Fang N, Srituravanich W, Durant S, Ambati M, Sun C, Zhang X 2005 New J. Phys. 7 255
Google Scholar
[6] Schurig D, Mock J J, Justice B J, Cummer S A, Pendry J B, Starr A F, Smith D R 2006 Science 314 977
Google Scholar
[7] Landy N I, Sajuyigbe S, Mock J J, Smith D R, Padilla W J 2008 Phys. Rev. Lett. 100 207402
Google Scholar
[8] Ye Y, He S 2010 Appl. Phys. Lett. 96 203501
Google Scholar
[9] Menzel C, Helgert C, Rockstuhl C, Kley E B, Tunnermann A, Pertsch T, Lederer F 2010 Phys. Rev. Lett. 104 253902
Google Scholar
[10] Shi H, Zhang A, Zheng S, Li J, Jiang Y 2014 Appl. Phys. Lett. 104 034102
Google Scholar
[11] Wang S, Liu W, Wen G 2018 Sci. Rep. 8 3791
Google Scholar
[12] Hao J, Yuan Y, Ran L, Jiang T, Kong J, Chan C T, Zhou L 2007 Phys. Rev. Lett. 99 063908
Google Scholar
[13] Feng M, Wang J, Ma H, Mo W, Ye H, Qu S 2013 J. Appl. Phys. 114 074508
Google Scholar
[14] Pu M, Chen P, Wang Y, Zhao Z, Huang C, Wang C, Ma X, Luo X 2013 Appl. Phys. Lett. 102 131906
Google Scholar
[15] Cheng Y Z, Withayachumnankul W, Upadhyay A, Headland D, Nie Y, Gong R Z, Bhaskaran M, Sriram S, Abbott D 2014 Appl. Phys. Lett. 105 181111
Google Scholar
[16] Zhang L, Zhou P, Chen H, Lu H, Xie J, Deng L 2015 Appl. Phys. B 120 617
Google Scholar
[17] Chen H, Wang J, Ma H, Qu S, Xu Z, Zhang A, Yan M, Li Y 2014 J. Appl. Phys. 115 154504
Google Scholar
[18] Ding J, Arigong B, Ren H, Zhou M, Shao J, Lin Y, Zhang H 2014 Opt. Express 22 29143
Google Scholar
[19] Shi H, Li J, Zhang A, Wang J, Xu Z 2014 Opt. Express 22 20973
Google Scholar
[20] Wen X, Zheng J 2014 Opt. Express 22 28292
Google Scholar
[21] 范亚, 屈绍波, 王甲富, 张介秋, 冯明德, 张安学 2015 64 184101
Google Scholar
Fan Y, Qu S B, Wang J F, Zhang J Q, Feng M D, Zhang A X 2015 Acta Phys. Sin. 64 184101
Google Scholar
[22] Gao X, Han X, Cao W, Li H, Ma H, Cui T 2015 IEEE Trans. Antennas Propag. 63 3522
Google Scholar
[23] Zhao J, Cheng Y 2017 Optik 136 52
Google Scholar
[24] 余积宝, 马华, 王甲富, 冯明德, 李勇峰, 屈绍波 2015 64 178101
Google Scholar
Yu J B, Ma H, Wang J F, Feng M D, Li Y F, Qu S B 2015 Acta Phys. Sin. 64 178101
Google Scholar
[25] Zhao J, Cheng Y 2016 Appl. Phys. B 122 255
[26] Ding F, Wang Z, He S, Shalaev V M, Kildishev A V 2015 ACS Nano 9 4111
Google Scholar
[27] Zhang L, Zhou P, Chen H, Lu H, Xie H, Zhang L, Li E, Xie J, Deng L 2016 Sci. Rep. 6 33826
Google Scholar
[28] Zhang L, Zhou P, Lu H, Zhang L, Xie J, Deng L 2016 Opt. Mater. Express 6 1393
Google Scholar
[29] Mei Z, Ma X, Lu C, Zhao Y 2017 AIP Adv. 7 125323
Google Scholar
[30] 方振华, 罗春荣, 赵晓鹏 2017 光子学报 46 1216001
Fang Z H, Luo C R, Zhao X P 2017 Acta Photon. Sin. 46 1216001
[31] Khan M I, Fraz Q, Tahir F A 2017 J. Appl. Phys. 121 045103
Google Scholar
[32] Li S, Cao X, Xu L, Zhou L, Yang H, Han J, Zhang Z, Zhang D, Liu X, Zhang C, Zheng Y, Zhao Y 2016 Sci. Rep. 5 37409
[33] Sui S, Ma H, Wang J, Feng M, Pang Y, Xia S, Xu Z, Qu S 2016 Appl. Phys. Lett. 109 014104
Google Scholar
[34] 韩江枫, 曹祥玉, 高军, 李思佳, 张晨 2016 65 044201
Google Scholar
Han J F, Cao X Y, Gao J, Li S J, Zhang C 2016 Acta Phys. Sin. 65 044201
Google Scholar
[35] Jia Y, Liu Y, Zhang W, Gong S 2016 Appl. Phys. Lett. 109 051901
Google Scholar
下载:
计量
- 文章访问数: 9715
- PDF下载量: 232
- 被引次数: 0
