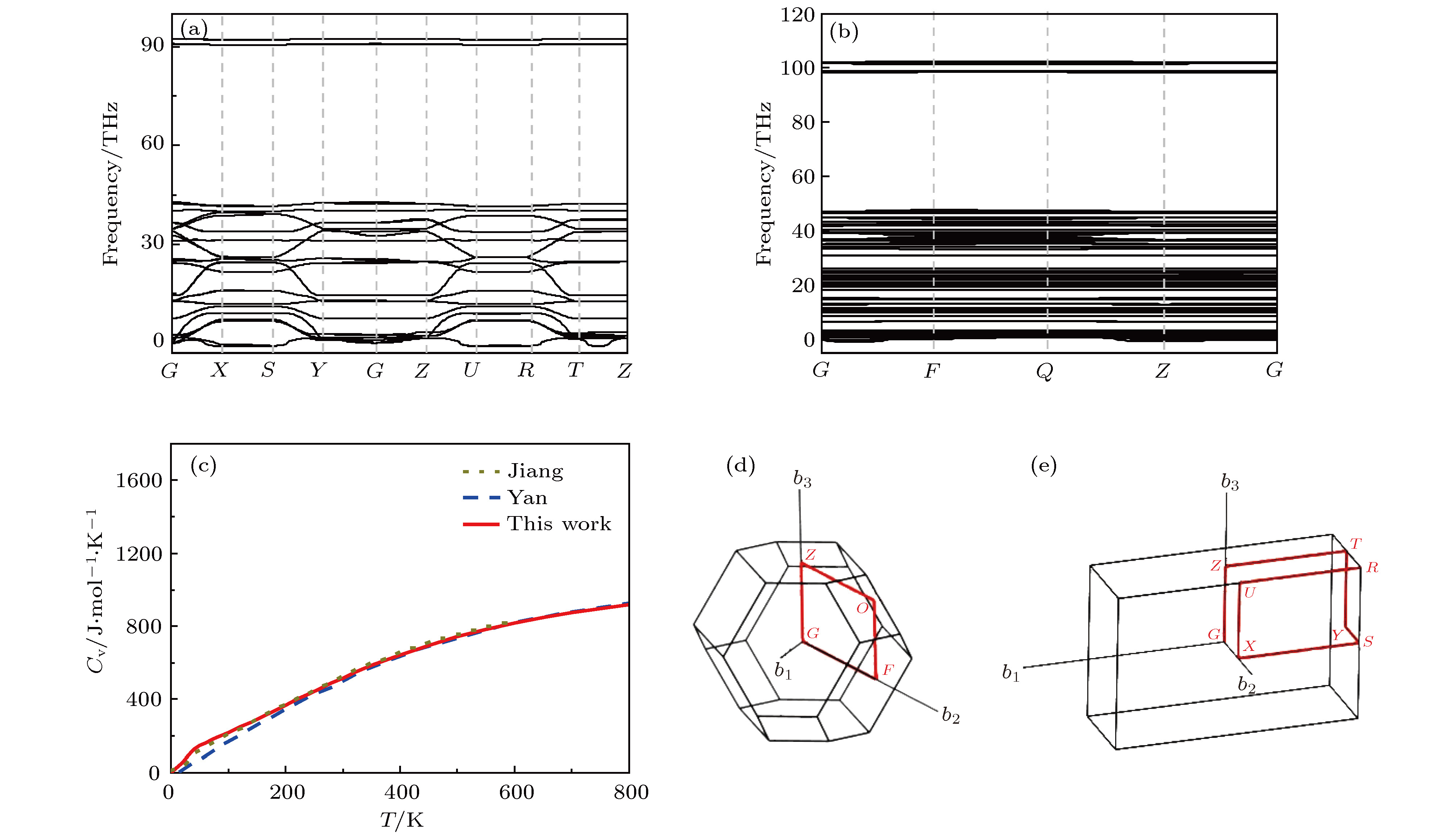
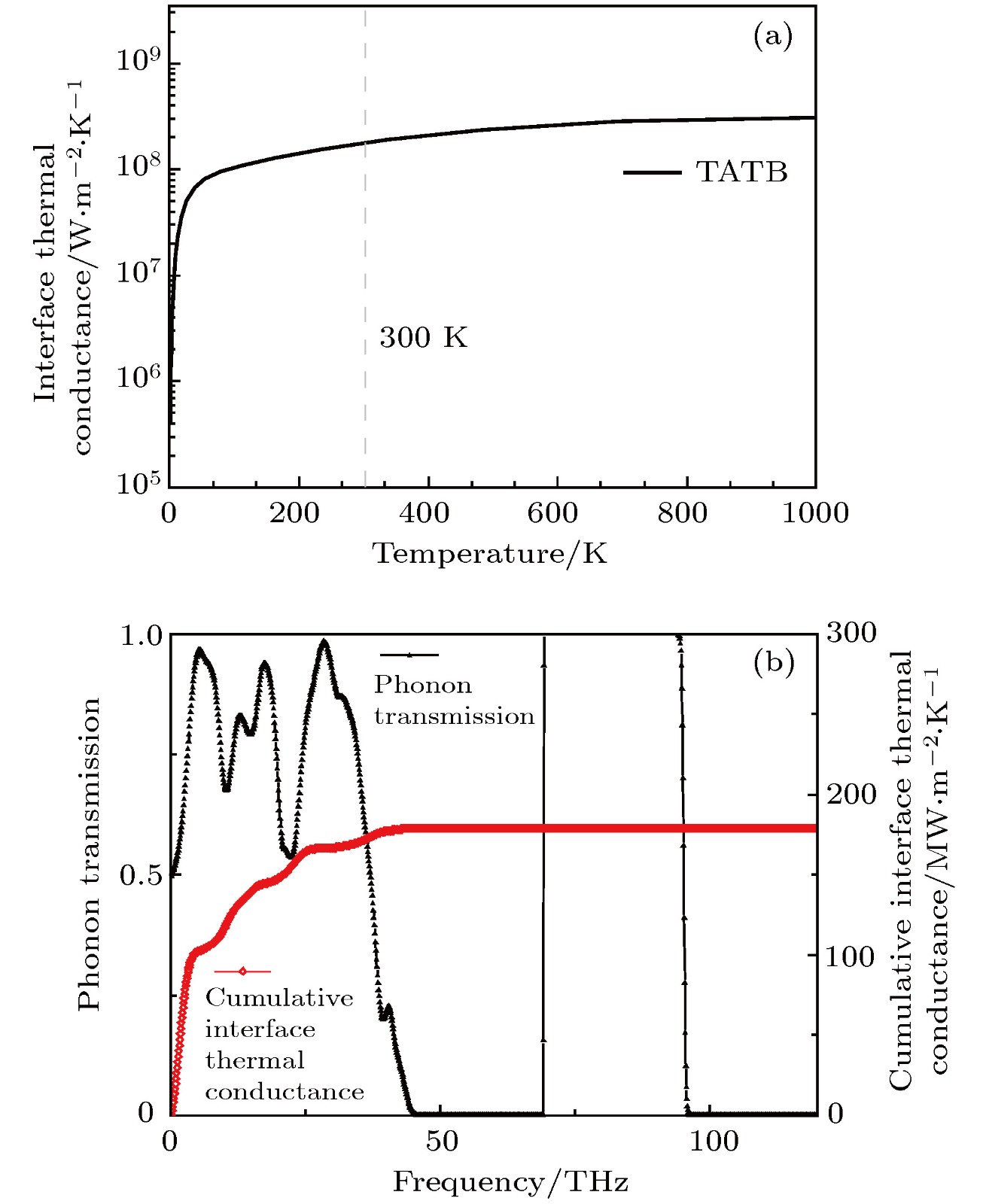
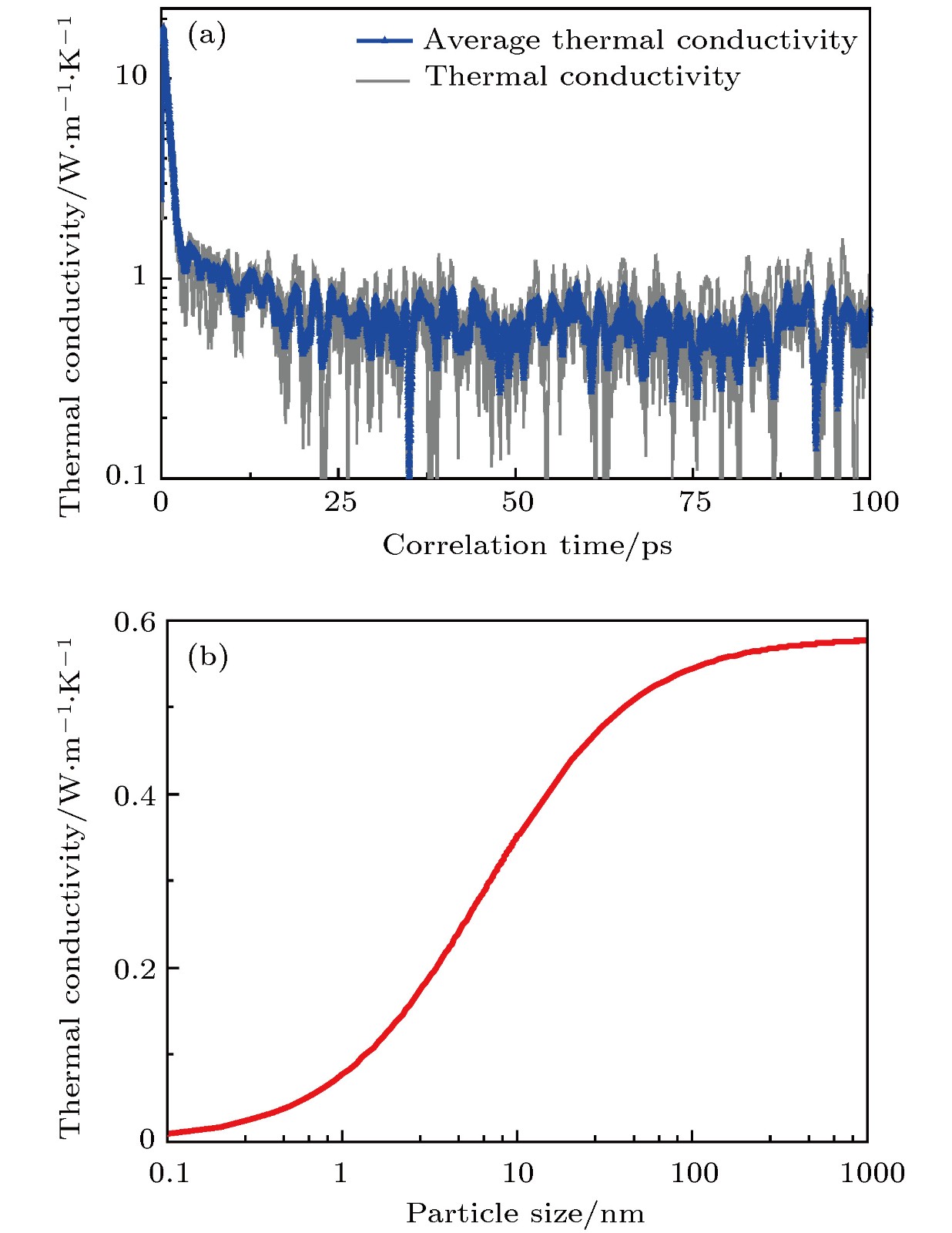
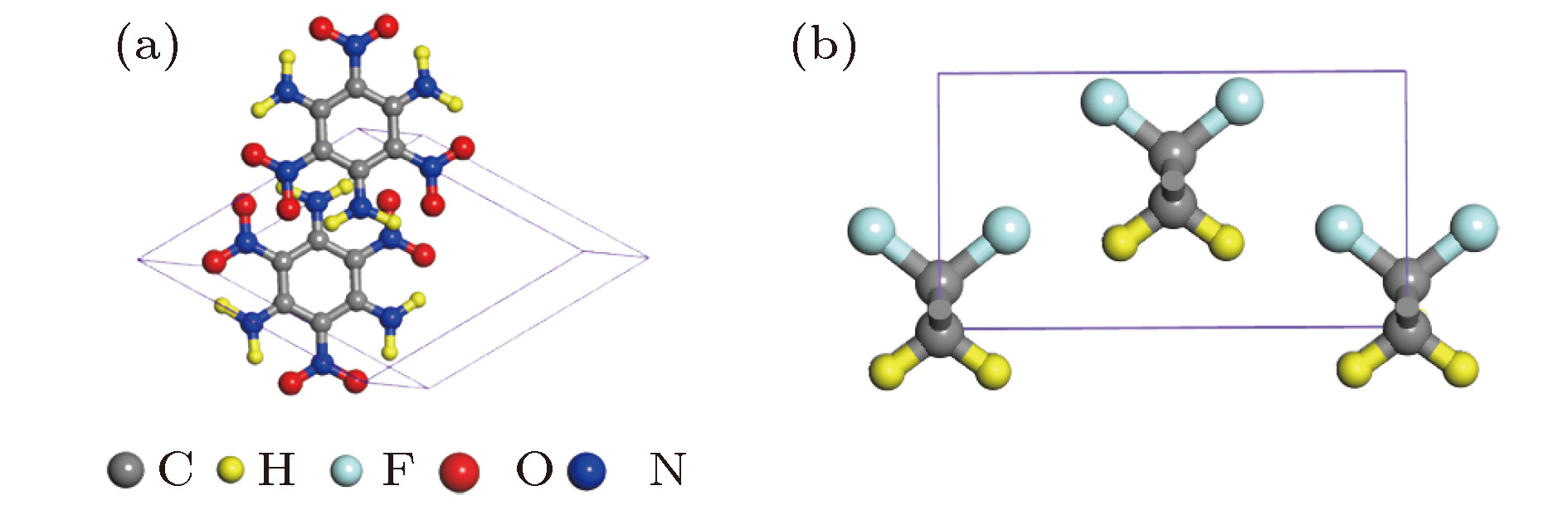
-
高聚物粘结炸药(PBX)的热力学性质是用于炸药结构响应、安全性评估、数值模拟分析等的重要参数. 由于PBX结构的多尺度特性, 完全采取实验方法精细表征这些参数存在巨大的挑战. 本文运用第一性原理和分子动力学计算的方法, 系统研究了三氨基三硝基苯(TATB)基高聚物粘结炸药的热力学参数和界面热传导性质. 利用散射失配模型研究了TATB与聚偏二氟乙烯(PVDF)界面的热传导过程, 发现热导率随温度升高而上升, 并且在高温情况下接近于定值. 基于分子动力学获得的TATB热导率并结合界面热导率, 分析了PBX炸药的热导与颗粒尺寸的关系, 当颗粒尺寸大于100 nm时, 界面热阻对于PBX热导率的影响有限.The thermodynamic properties of insensitive high explosive 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) based polymer bonded explosives (PBXs) are investigated by using first principle calculation and molecular dynamics simulation. The results include the phonon dispersion relations, interface thermal conductances, and thermal conductivities of TATB based PBXs. Both TATB and PVDF structures are optimized, in which the optimized lattice constants accord with previous results. The phonon dispersion relation of TATB and PVDF are calculated based on lattice dynamics. All interatomic force constants are calculated by the finite displacement method (numerical derivatives from perturbed supercells). The calculated phonon dispersion relation of TATB and heat capacity are in general agreement with experimental and theoretical results. The imaginary frequencies are observed in both TATB and PVDF dispersion relation. The imaginary frequencies are mainly due to the smaller calculated supercell size and temperature effect. The phonon mode of TATB and PVDF are assigned at Γ point. Based on the calculated phonon dispersion, some information including heat capacity, phonon density of states and phonon mode assignment is derived. The TATB possesses 144 phonon modes including 3 acoustic-phonon modes and 141 optical phonon modes. The anylized phonon mode of TATB shows that -NO2 dominates the phonon DOS in low frequency zone, phenyl rings dominate in middle frequency zone and -NH2 dominates in high frequency zone. By analyzing the phonon density of states and capacity, both TATB and PVDF imply that low-frequency vibration dominates the thermal conductivity. The thermal conductivity is determined for TATB by using the equlibrium molecular dynamics method and an established TATB force field. The TATB model is built with 2880 atoms. The structure of TATB is optimized by using molecular mechanics, then this system is relaxed by using a Nose-Hoover thermostat and barostat with a damping factor of 50 fs cin time steps of 0.1 fs. The calcultated thermal conductivity at room temperature shows good agreement with experimental result. The interface thermal conductance of TATB-PVDF is calculated by using a diffusive mismatch model. The interface thermal transport still follows Fourier’s law of heat conduction, and ballistic thermal transport mechanism is not involved. By using the above results, the thermal conductivity of mixture TATB-PVDF system is analized with a simple series model. The particle size smaller than 100 nm significantly suppresses the mixture system thermal conductivity.
-
Keywords:
- triaminotrinitrobenzene /
- first principle calculation /
- molecular dynamics /
- thermodynamic properties
[1] 董海山, 周芬芬1989 高能炸药及相关物性能(北京: 科学出版社)第2页
Dong H S, Zhou F F 1989 High Energy Explosive Property (Beijing: Science Press) p2 (in Chinese)
[2] 李尚困, 黄西成, 王鹏飞 2016 火炸药学报 39 001
Li S K, Huang X C, Wang P F 2016 Chin. J. Explos. Propellants 39 001
[3] Voigt-Martin I G, Li G, Yakimanski A, Schulz G, Jens Wolff J J 1996 J. Am. Chem. Soc. 118 12830
Google Scholar
[4] Brill T B, James K J 1993 Chem. Rev. 93 2667
Google Scholar
[5] Zyss J, Ledoux I 1994 Chem. Rev. 94 77
Google Scholar
[6] He G S, Yang Z J, Zhou X Y, Zhang J H, Pan L P, Liu S J 2016 Comp. Sci. Tech. 131 22
Google Scholar
[7] Siviour C R, Gifford M J, Waller S M, Proud W G, Field J E 2004 J. Mater. Sci. 39 1255
Google Scholar
[8] Lin C M, He G S, Liu J H, Pan L P, Liu S J 2015 RSC Adv. 5 98514
Google Scholar
[9] Gee R H, Roszak S, Balasubramanian K, Fried L E 2004 J. Chem. Phys. 120 7059
Google Scholar
[10] Bedrov D, Borodin O, Smith G D, Sewell T D, Dattelbaum D M 2009 J. Chem. Phys. 131 224703
Google Scholar
[11] Stevens L L, Velisavljevic N, Hooks D E, Dattelbaum D M 2008 Propell. Explos. Pyrot. 33 286
Google Scholar
[12] Rykounov A A 2015 J. Appl. Phys. 117 215901
Google Scholar
[13] Kroonblawd M P, Sewell T D 2013 J. Chem. Phys. 139 074503
Google Scholar
[14] Kroonblawd M P, Sewell T D 2014 J. Chem. Phys. 141 184501
Google Scholar
[15] Fan H, Long Y, Ding L, Chen J, Nie F D 2017 Comp. Mater. Sci. 131 321
Google Scholar
[16] 蒋文灿, 陈华, 张伟斌 2016 65 126301
Google Scholar
Jiang W C, Chen H, Zhang W B 2016 Acta Phys. Sin. 65 126301
Google Scholar
[17] Wu Z Q, Mou W W, Kalia R, Nakano A, Vashishta P 2015 Int. J. Energ. Mater. Chem. Prop. 14 519
[18] Liu H, Zhao J, Ji G, Wei D, Gong Z 2006 Phys. Lett. A 358 63
Google Scholar
[19] Long Y, Chen J 2014 Model. Simul. Mater. Sci. Eng. 22 035013
Google Scholar
[20] Long Y, Chen J 2018 Model. Simul. Mater. Sci. Eng. 26 015002
Google Scholar
[21] Born M, Huang K 1954 Dynamical Theory of Crystal Lattices (Oxford: Oxford University Press) p38
[22] 程和平, 陈光华, 覃睿, 但加坤, 黄智蒙, 彭辉, 陈图南, 雷江波 2014 物理化学学报 30 281
Google Scholar
Cheng H P, Chen G H, Qin R, Dan J K, Huang Z M, Peng H, Chen T N, Lei J B 2014 Acta Phys. Chim. Sin. 30 281
Google Scholar
[23] Hasegawa R, Takahashi Y, Chatani Y, Tadokoro H 1972 Polym. J. 3 600
Google Scholar
[24] Kunc K, Louis S G 1985 Electronic Structure, Dynamics, and Quantum Structural Properties of Condensed Matter (New York: Springer US) p227, p335
[25] Kresse G, Hafner J 1993 Phys. Rev. B 47 558
Google Scholar
[26] Blochl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[27] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[28] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[29] Perdew J P, Burke K, Ernzerhof M 1997 Phys. Rev. Lett. 78 1396
[30] Togo A, Tanaka I 2015 Scr. Mater. 108 1
Google Scholar
[31] 鲍华 2013 62 186302
Google Scholar
Bao H 2013 Acta Phys. Sin. 62 186302
Google Scholar
[32] Bellis L D, Phelan P E, Prasher R S 2000 J. Thermophys. Heat. Tr. 14 144
Google Scholar
[33] Swartz E T, Pohl R O 1989 Rev. Mod. Phys. 61 605
Google Scholar
[34] Kubo R 1966 Rep. Prog. Phys. 29 255
[35] Green M S 1954 J. Chem. Phys. 22 398
Google Scholar
[36] Kubo R 1957 J. Phys. Soc. Jpn. 12 570
Google Scholar
[37] Long Y, Chen J 2014 J. Appl. Phys. 116 033516
Google Scholar
[38] Long Y, Liu Y G, Nie F D, Chen J 2012 Model. Simul. Mater. Sci. Eng. 20 065010
Google Scholar
[39] Plimpton S 1995 J. Comp. Phys. 117 1
Google Scholar
[40] Mcgrane S, Shreve A 2003 J. Chem. Phys. 119 5834
Google Scholar
[41] Olinger B W, Cady H H 1976 Conference: 6. Symposium on Detonation San Diego, California, August 24－27, 1976
[42] Dobratz B M 1995 The Insensitive High Explosive Triaminotrinitrobenzene (TATB): Development and Characterization—1888 to 1994, Report no. LA-13014-H, 1995p33
-
图 2 (a), (b) TATB和PVDF声子色散曲线; (c) TATB晶格热容随温度的变化; (d), (e) TATB和PVDF第一布里渊区高对称点积分路径
Fig. 2. The phonon dispersion relation of TATB (a), and PVDF (b); (c) the heat capacity of TATB as a function of temperature; the Brillouin zone and high symmetry points of TATB (d), and PVDF (e).
图 3 (a), (b) TATB和PVDF的Γ点声子模分析; (c), (d) TATB和PVDF的加权声子态密度和声子态密度(小图)
Fig. 3. Decomposition of the gamma-point eigenmodes of TATB (a), and PVDF (b); the weighted phonon density of states of TATB (c), and PVDF (d).
图 4 (a) TATB-PVDF界面热导率随温度变化情况; (b) TATB-PVDF界面声子透射率(黑)和累积热导率(红)
Fig. 4. (a) The interface thermal conductance of TATB-PVDF as a function of temperature; (b) phonon transmission of TATB-PVDF interface as a function of frequency.
图 5 (a) EMD方法计算TATB热导率结果; (b) TATB基PBX炸药热导率随颗粒尺寸的变化
Fig. 5. (a) EMD calculation of TATB thermal conductivity; (b) thermal conductivity of TATB-based PBXs as a function of particle size.
表 1 TATB部分Raman活性模计算数值与文献结果的比较
Table 1. Comparison of the Raman modes of TATB crystal obtained in the present and previous calculations with experimental results.
声子模 本文工作 蒋文灿等[16] Liu等[18]/cm–1 Exp.[40]/cm–1 不可约表示 波数/cm–1 偏差/% 波数/cm–1 偏差/% Q27 283 –4.30 288 –2.70 292 296 E′ Q30 284 –4.32 289 –2.69 295 297 E′ Q32 330 –0.45 331 –0.30 312 332 E″ Q33 331 –1.01 332 –0.59 318 334 E″ Q36 352 –4.53 359 –2.71 370 369 E′ Q38 354 –4.55 362 –2.42 371 371 E′ Q42 380 –2.72 382 –2.30 391 391 ${\rm{A}}_2'$ Q44 431 –3.19 440 –1.12 436 445 E′ Q46 432 –3.88 441 –1.78 438 449 E′ Q50 507 –3.27 518 –1.14 520 524 E′ Q64 699 –0.72 680 –3.41 704 704 E′ Q65 700 –0.72 696 –1.27 708 705 E′ Q88 869 –0.28 846 –2.87 870 871 E′ Q89 872 –0.39 851 –2.74 874 875 E′ Q91 1027 –0.06 996 –3.11 1026 1028 E′ Q94 1029 –0.23 1001 –2.91 1032 1031 E′ Q105 1217 0.14 1154 –5.02 1215 1215 E′ Q107 1221 0.19 1162 –4.67 1219 1219 E′ Q109 1308 –0.34 1244 –5.18 1320 1312 E′ Q111 1313 –0.35 1250 –5.16 1327 1318 E′ Q119 1442 –0.33 1407 –2.76 1446 1447 E′ Q127 1551 –0.93 1542 –1.53 1575 1566 ${\rm{A}}_1'$ Q129 1560 –2.07 1548 –2.82 1586 1593 E′ Q130 1564 –2.33 1549 –3.25 1596 1601 E′ Q134 3281 2.39 3325 3.78 3313 3204 E′ Q138 3298 2.66 3351 4.29 3334 3213 ${\rm{A}}_1'$ Q142 3399 2.91 3439 4.12 3436 3303 E′ 
下载: 导出CSV
-
[1] 董海山, 周芬芬1989 高能炸药及相关物性能(北京: 科学出版社)第2页
Dong H S, Zhou F F 1989 High Energy Explosive Property (Beijing: Science Press) p2 (in Chinese)
[2] 李尚困, 黄西成, 王鹏飞 2016 火炸药学报 39 001
Li S K, Huang X C, Wang P F 2016 Chin. J. Explos. Propellants 39 001
[3] Voigt-Martin I G, Li G, Yakimanski A, Schulz G, Jens Wolff J J 1996 J. Am. Chem. Soc. 118 12830
Google Scholar
[4] Brill T B, James K J 1993 Chem. Rev. 93 2667
Google Scholar
[5] Zyss J, Ledoux I 1994 Chem. Rev. 94 77
Google Scholar
[6] He G S, Yang Z J, Zhou X Y, Zhang J H, Pan L P, Liu S J 2016 Comp. Sci. Tech. 131 22
Google Scholar
[7] Siviour C R, Gifford M J, Waller S M, Proud W G, Field J E 2004 J. Mater. Sci. 39 1255
Google Scholar
[8] Lin C M, He G S, Liu J H, Pan L P, Liu S J 2015 RSC Adv. 5 98514
Google Scholar
[9] Gee R H, Roszak S, Balasubramanian K, Fried L E 2004 J. Chem. Phys. 120 7059
Google Scholar
[10] Bedrov D, Borodin O, Smith G D, Sewell T D, Dattelbaum D M 2009 J. Chem. Phys. 131 224703
Google Scholar
[11] Stevens L L, Velisavljevic N, Hooks D E, Dattelbaum D M 2008 Propell. Explos. Pyrot. 33 286
Google Scholar
[12] Rykounov A A 2015 J. Appl. Phys. 117 215901
Google Scholar
[13] Kroonblawd M P, Sewell T D 2013 J. Chem. Phys. 139 074503
Google Scholar
[14] Kroonblawd M P, Sewell T D 2014 J. Chem. Phys. 141 184501
Google Scholar
[15] Fan H, Long Y, Ding L, Chen J, Nie F D 2017 Comp. Mater. Sci. 131 321
Google Scholar
[16] 蒋文灿, 陈华, 张伟斌 2016 65 126301
Google Scholar
Jiang W C, Chen H, Zhang W B 2016 Acta Phys. Sin. 65 126301
Google Scholar
[17] Wu Z Q, Mou W W, Kalia R, Nakano A, Vashishta P 2015 Int. J. Energ. Mater. Chem. Prop. 14 519
[18] Liu H, Zhao J, Ji G, Wei D, Gong Z 2006 Phys. Lett. A 358 63
Google Scholar
[19] Long Y, Chen J 2014 Model. Simul. Mater. Sci. Eng. 22 035013
Google Scholar
[20] Long Y, Chen J 2018 Model. Simul. Mater. Sci. Eng. 26 015002
Google Scholar
[21] Born M, Huang K 1954 Dynamical Theory of Crystal Lattices (Oxford: Oxford University Press) p38
[22] 程和平, 陈光华, 覃睿, 但加坤, 黄智蒙, 彭辉, 陈图南, 雷江波 2014 物理化学学报 30 281
Google Scholar
Cheng H P, Chen G H, Qin R, Dan J K, Huang Z M, Peng H, Chen T N, Lei J B 2014 Acta Phys. Chim. Sin. 30 281
Google Scholar
[23] Hasegawa R, Takahashi Y, Chatani Y, Tadokoro H 1972 Polym. J. 3 600
Google Scholar
[24] Kunc K, Louis S G 1985 Electronic Structure, Dynamics, and Quantum Structural Properties of Condensed Matter (New York: Springer US) p227, p335
[25] Kresse G, Hafner J 1993 Phys. Rev. B 47 558
Google Scholar
[26] Blochl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[27] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
[28] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[29] Perdew J P, Burke K, Ernzerhof M 1997 Phys. Rev. Lett. 78 1396
[30] Togo A, Tanaka I 2015 Scr. Mater. 108 1
Google Scholar
[31] 鲍华 2013 62 186302
Google Scholar
Bao H 2013 Acta Phys. Sin. 62 186302
Google Scholar
[32] Bellis L D, Phelan P E, Prasher R S 2000 J. Thermophys. Heat. Tr. 14 144
Google Scholar
[33] Swartz E T, Pohl R O 1989 Rev. Mod. Phys. 61 605
Google Scholar
[34] Kubo R 1966 Rep. Prog. Phys. 29 255
[35] Green M S 1954 J. Chem. Phys. 22 398
Google Scholar
[36] Kubo R 1957 J. Phys. Soc. Jpn. 12 570
Google Scholar
[37] Long Y, Chen J 2014 J. Appl. Phys. 116 033516
Google Scholar
[38] Long Y, Liu Y G, Nie F D, Chen J 2012 Model. Simul. Mater. Sci. Eng. 20 065010
Google Scholar
[39] Plimpton S 1995 J. Comp. Phys. 117 1
Google Scholar
[40] Mcgrane S, Shreve A 2003 J. Chem. Phys. 119 5834
Google Scholar
[41] Olinger B W, Cady H H 1976 Conference: 6. Symposium on Detonation San Diego, California, August 24－27, 1976
[42] Dobratz B M 1995 The Insensitive High Explosive Triaminotrinitrobenzene (TATB): Development and Characterization—1888 to 1994, Report no. LA-13014-H, 1995p33
下载:
计量
- 文章访问数: 10268
- PDF下载量: 110
- 被引次数: 0
