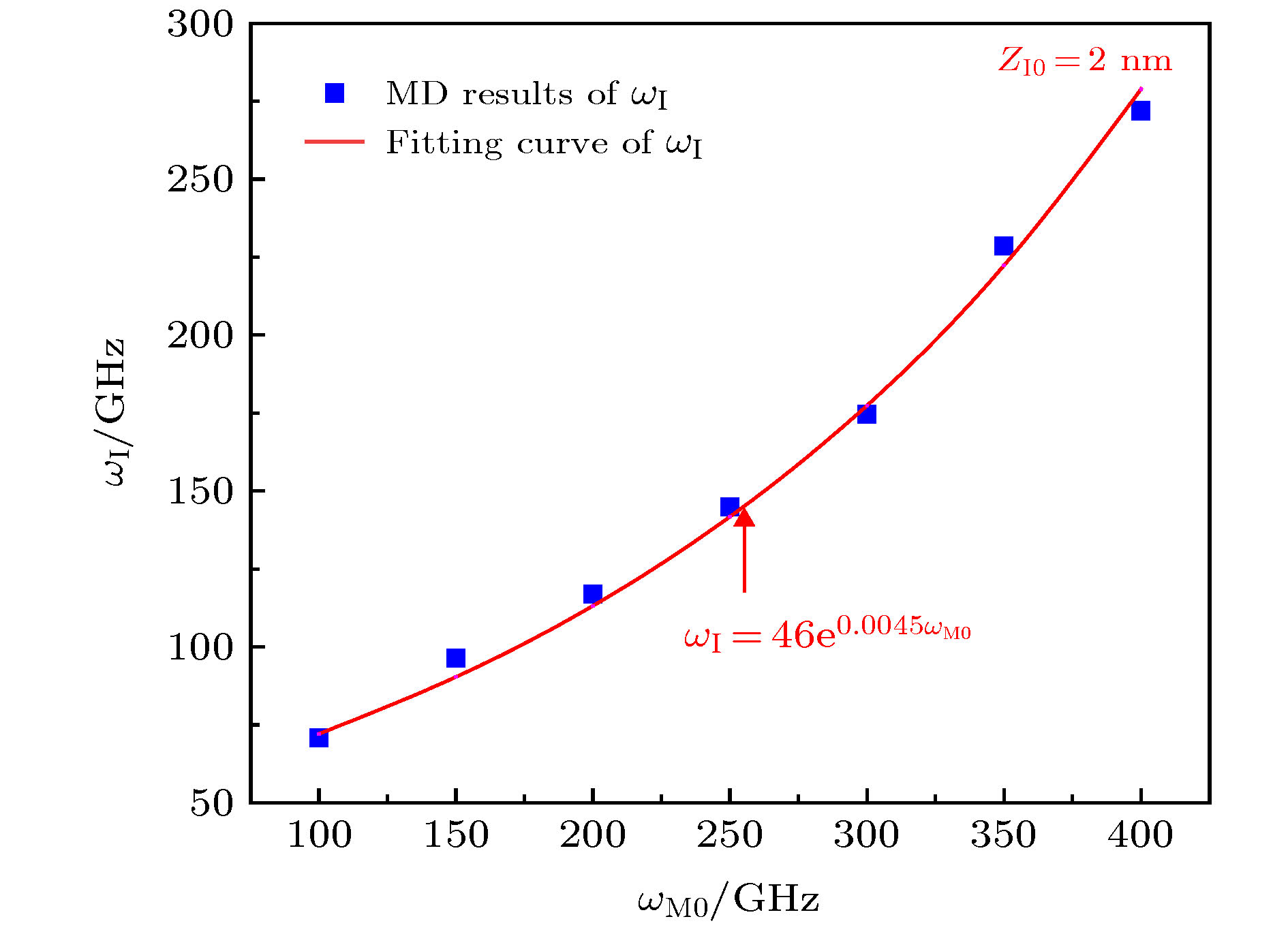
-
本文提出了一种新型的三壁碳纳米管螺旋振荡器, 通过对内管施加轴向激励和中管施加旋转激励的方式, 来同时获得内管和中管的螺旋信号输出. 采用分子动力学方法研究了该振荡器在拉转耦合下的振荡行为. 在模拟过程中, 固定的外管充当振荡器定子的作用, 内管和中管在分别施加一定的初始激励后保持自由振荡. 模拟结果表明, 在内管拉出距离一定的情况下, 内管的自激发旋转频率随着中管初始旋转激励频率的增加而增加, 且最终趋于一个稍低于旋转激励的稳定值. 当施加的初始旋转频率在400 GHz以内时, 内管达到稳定的旋转频率
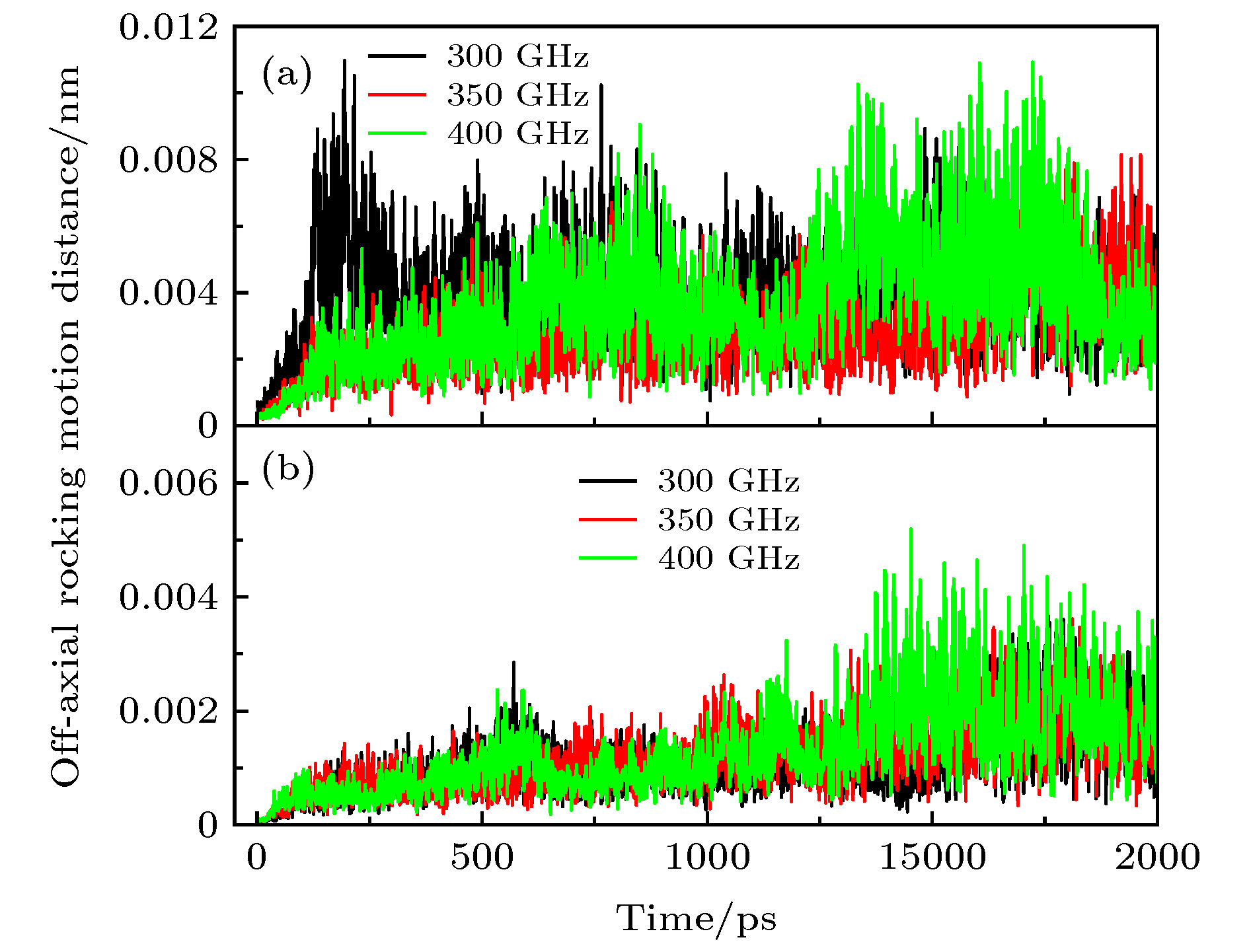
$ {\omega _{{\rm{ I}}}}$ 与旋转激励频率$ {\omega _{{\rm{ M 0}}}}$ 的关系为$ {\omega _{{\rm{ I}}}} = 46{{\rm{e}}^{0.0045{\omega _{{\rm{M 0}}}}}}$ . 尽管提高初始旋转激励频率可以提高内管的旋转频率, 但随着中管初始旋转频率的增加内管的轴向性能下降, 不稳定振荡加剧. 同时中管轴向振荡的稳定性与施加在其上面的初始旋转激励的频率有关, 过高的初始旋转频率不仅会加大非轴向摆动距离, 导致轴向振荡性能下降, 而且旋转损耗比也将随着初始旋转频率的增加而增加. 因此, 合理的控制初始旋转频率的幅值是设计低损耗三壁碳纳米管螺旋振荡器的关键.A novel triple-walled carbon nanotube (TWCNT) screwing oscillator is proposed, in which screwing motion signals of both inner tube and middle tube are outputted simultaneously by applying an axial excitation to the inner tube and a rotating excitation to the middle tube. The molecular dynamic method is used to investigate the oscillatory behavior of the TWCNT oscillator under screwing motion. In the simulation process, the fixed outer tube acts as the oscillator stator, while the inner tube and the middle tube keep free oscillation after applying a certain initial excitation respectively. The simulation results show that the rotation frequency of the inner tube increases with the increase of the initial rotation excitation frequency of the middle tube when the inner tube is pulled out at a certain distance, and eventually tends to a stable value slightly lower than the rotation excitation. When the applied initial rotation frequency is within 400 GHz, the self-excited stable ration frequency ($ {\omega _{\rm{I}}}$ ) of the inner tube can be expressed as a function of the initial rotation excitation frequency ($ {\omega _{{\rm{M}}0}}$ ),$ {\omega _{\rm{I}}} = 46{{\rm{e}}^{0.0045{\omega _{{\rm{M0}}}}}}$ . Although increasing the initial rotation excitation frequency can enhance the rotation frequency of the inner tube, as the initial rotation frequency of the middle tube increases, the axial performance of the inner tube is degraded and the unstable oscillations is aggravated. At the same time, the stability of the axial oscillation of the middle tube is related to the frequency of the initial rotational excitation applied to it. Too high an initial rotational frequency will not only increase the off-axis rocking motion distance, resulting in a degradation in axial oscillation performance, but also the rotation loss will increase as the initial rotation frequency increases. Therefore, a reasonable control of the amplitude of the initial rotation frequency is the key to designing a low-loss TWCNTs screwing oscillator.-
Keywords:
- triple-walled carbon nanotube /
- screwing motion /
- pull-rotate coupling /
- molecular dynamics
[1] Iijima S 1991 Nature 354 56
Google Scholar
[2] Zou J, Ji B, Feng X Q, Gao H J 2006 Nano Lett. 6 430
Google Scholar
[3] Huang Z 2008 Nanotechnology 19 045701
Google Scholar
[4] Bailey S W D, Amanatidis I, Lambert C J 2008 Phys. Rev. Lett. 100 256802
Google Scholar
[5] Yang W D, Wang X, Fang C Q 2015 Composites Part B 82 143
Google Scholar
[6] Chiu H Y, Hung P, Postma H W C, Bockrath M 2008 Nano Lett. 8 4342
Google Scholar
[7] Qin Z, Zou J, Feng X Q 2008 J. Comput. Theor. Nanosci. 5 1403
Google Scholar
[8] Legoas S B, Coluci V R, Braga S F, Coura P Z, Dantas S O, Galvão D S 2004 Nanotechnology 15 S184
Google Scholar
[9] Legoas S B, Coluci V R, Braga S F, Coura P Z, Dantas S O, Galvao D S 2003 Phys. Rev. Lett. 90 055504
Google Scholar
[10] Cumings J, Zettl A 2000 Science 289 602
Google Scholar
[11] Zheng Q, Liu J Z, Jiang Q 2002 Phys. Rev. B 65 245409
Google Scholar
[12] Cai K, Yin H, Qin Q H, Li Y 2014 Nano Lett. 14 2558
Google Scholar
[13] Servantie J, Gaspard P 2006 Phys. Rev. Lett. 97 13831
[14] Cook E H, Buehler M J, Spakovszky Z S 2013 J. Mech. Phys. Solids. 61 652
Google Scholar
[15] Zhao Y, Ma C C, Chen G, Jiang Q 2003 Phys. Rev. Lett. 91 175504
Google Scholar
[16] Guo W L, Guo Y F, Gao H J, Zheng Q S 2003 Phys. Rev. Lett. 91 125501
Google Scholar
[17] Kang J W, Lee J H 2008 Nanotechnology 19 285704
Google Scholar
[18] Liu P, Zhang Y W, Lu C 2005 J. Appl. Phys. 98 014301
Google Scholar
[19] Liu P, Zhang Y W, Lu C J 2006 Carbon 44 27
Google Scholar
[20] Chen L, Jiang W G, Zou H, Feng X Q, Qin Q H, Li X 2019 Phys. Lett. A. 383 2309
Google Scholar
[21] Lin Y W, Jiang W G, Qin Q H, Chen Y J 2019 Appl. Phys. Express. 12 065001
Google Scholar
[22] Voter A F, Doll J D 1984 J. Chem. Phys. 80 5832
Google Scholar
[23] Harrison J A, White C T, Colton R J, Brenner D W 1992 Phys. Rev. B. 46 9700
Google Scholar
[24] Brenner D W, Shenderove O A, Harrison J A, Stuart S J, Ni B, Sinnott S B 2002 J. Phys. Condens. Matter 14 783
Google Scholar
[25] Zou J, Ji B H, Feng X Q, Gao H J 2006 Small 2 1348
Google Scholar
[26] Doll J D 1982 J. Chem. Phys. 77 479
Google Scholar
[27] Lammps molecular dynamics simulator, http://lammps.sandia.gov, 2014 [2020-5-31]
[28] 邹航2019 硕士学位论文 (南昌: 南昌航空大学)
Zhou H 2019 M. S. Thesis (Nanchang: Nanchang Hangkong University) (in Chinese)
-
图 1 三壁碳纳米管振荡器模型示意图 (a) 三视图; (b) 俯视图; (c) 螺旋运动示意图
Fig. 1. Schematic diagram of the triple-walled carbon nanotubes oscillator model: (a) Three view; (b) vertical view (c) screwing motion.
图 2 NVE过程中不同
${\omega _{{\rm{M0}}}}$ 下的中管质心位置的历程图Fig. 2. Histories of position of mass center of middle tubes (MCMTs) with different
${\omega _{{\rm{M0}}}}$ during the NVE process.
图 3 NVE过程中不同
${\omega _{{\rm{M0}}}}$ 下中管的偏轴距离Fig. 3. The off-axis rocking motion distance of the MCMTs with different
${\omega _{{\rm{M0}}}}$ during the NVE process.
图 4 中管
${\omega _{{\rm{M0}}}}$ 在螺旋运动过程中的损耗情况Fig. 4. Rotational frequency dissipation of the MCMTs with different
${\omega _{{\rm{M0}}}}$ during the screwing motion.
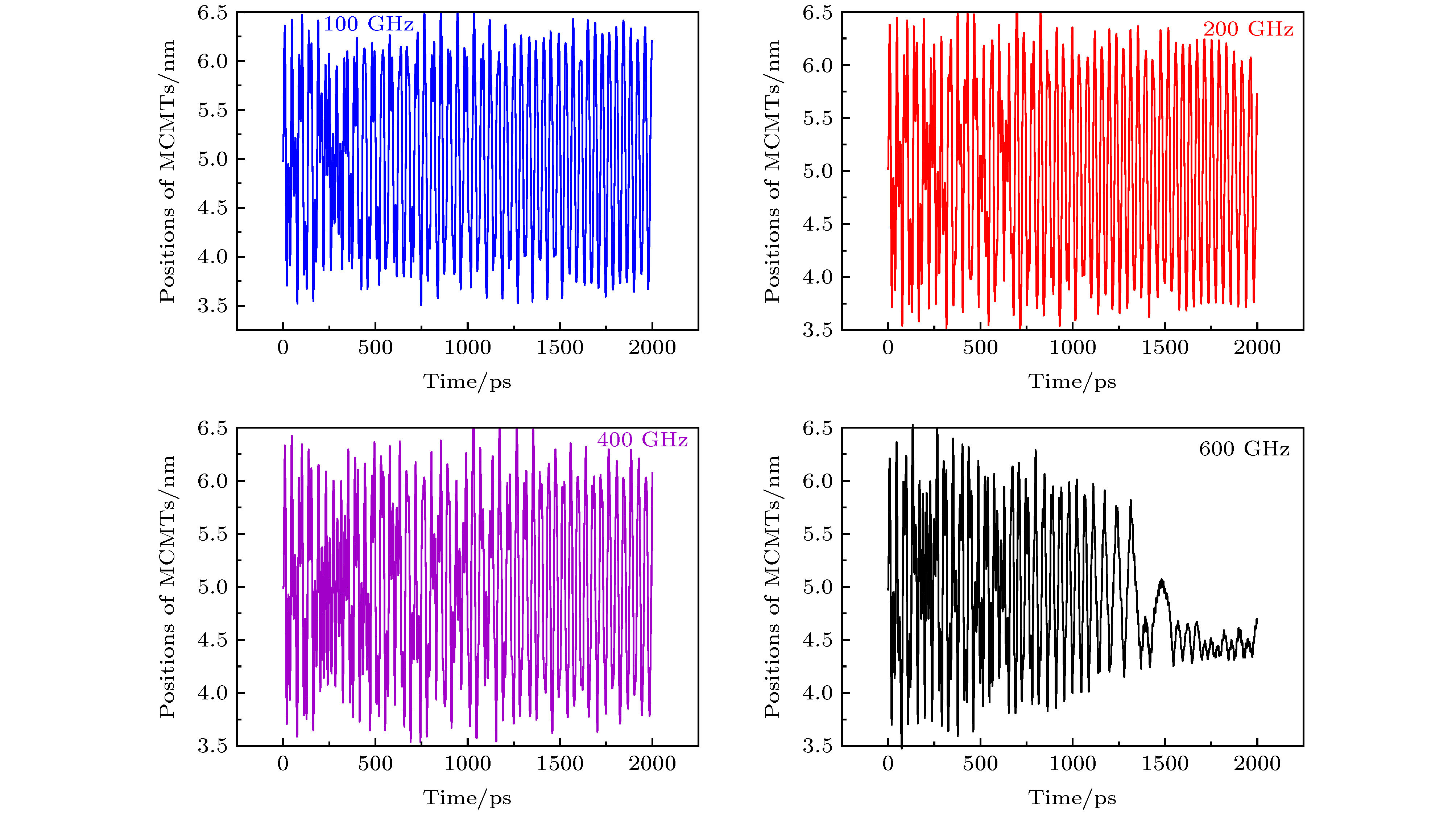
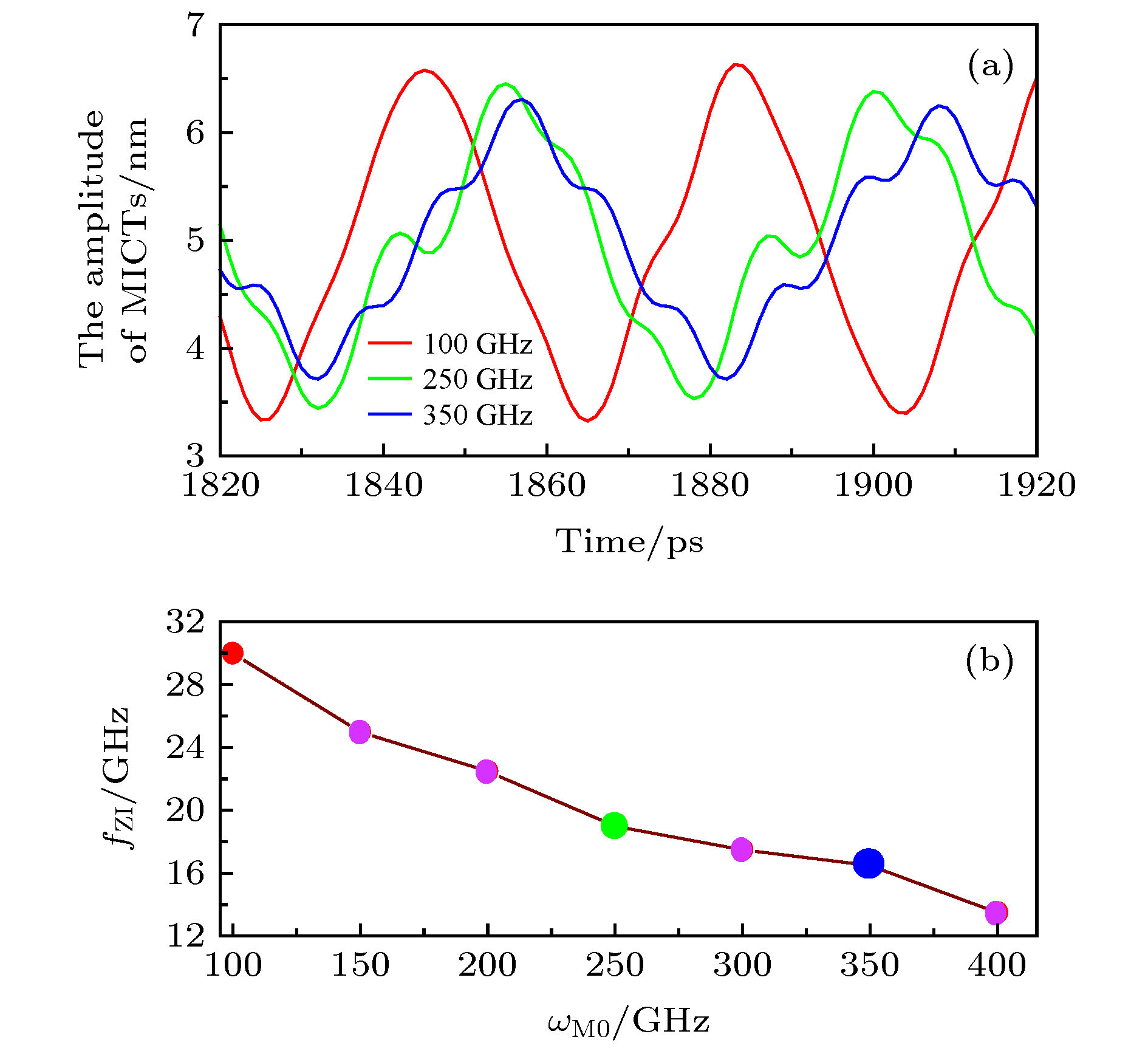
图 5 内管的轴向振荡 (a) NVE过程中不同
${\omega _{{\rm{M0}}}}$ 下的内管质心位置变化曲线; (b)内管平均振荡频率${f_{{\rm{ZI}}}}$ 随${\omega _{{\rm{M0}}}}$ 的变化Fig. 5. Axial oscillations of the inner tube: (a) Changes of the position of mass center of inner tubes(MCITs) with different
${\omega _{{\rm{M0}}}}$ in the NVE process; (b)${f_{{\rm{ZI}}}}$ with respect to${\omega _{{\rm{M0}}}}$ .
图 6 NVE过程中不同
${\omega _{{\rm{M0}}}}$ 下两管质心的偏轴距离 (a)内管质心; (b)中管质心Fig. 6. The Off-axis rocking motion distance of mass center of (a) inner tube and (b) middle tube with different
${\omega _{{\rm{M0}}}}$ during the NVE process.
图 7 NVE过程中
${\omega _{{\rm{M0}}}}$ 下内管的旋转频率Fig. 7. Rotation frequency of the inner tube with different
${\omega _{{\rm{M0}}}}$ during the NVE process.
图 8
${\omega _{\rm{I}}}$ 与${\omega _{{\rm{M0}}}}$ 的关系曲线Fig. 8. Change of
${\omega _{\rm{I}}}$ as a function of${\omega _{{\rm{M0}}}}$ .表 1 碳纳米管的几何参数
Table 1. Geometric parameters of the carbon nanotubes.
碳管手性(n, m)@(n, m)@(n, m) 管长/nm 管半径/nm 管间距/nm 原子数 (9, 9)@(24, 0) @(19, 19) 6/6/4 1.220/1.879/2.576 0.329/0.349 864/1344/1216 
下载: 导出CSV
-
[1] Iijima S 1991 Nature 354 56
Google Scholar
[2] Zou J, Ji B, Feng X Q, Gao H J 2006 Nano Lett. 6 430
Google Scholar
[3] Huang Z 2008 Nanotechnology 19 045701
Google Scholar
[4] Bailey S W D, Amanatidis I, Lambert C J 2008 Phys. Rev. Lett. 100 256802
Google Scholar
[5] Yang W D, Wang X, Fang C Q 2015 Composites Part B 82 143
Google Scholar
[6] Chiu H Y, Hung P, Postma H W C, Bockrath M 2008 Nano Lett. 8 4342
Google Scholar
[7] Qin Z, Zou J, Feng X Q 2008 J. Comput. Theor. Nanosci. 5 1403
Google Scholar
[8] Legoas S B, Coluci V R, Braga S F, Coura P Z, Dantas S O, Galvão D S 2004 Nanotechnology 15 S184
Google Scholar
[9] Legoas S B, Coluci V R, Braga S F, Coura P Z, Dantas S O, Galvao D S 2003 Phys. Rev. Lett. 90 055504
Google Scholar
[10] Cumings J, Zettl A 2000 Science 289 602
Google Scholar
[11] Zheng Q, Liu J Z, Jiang Q 2002 Phys. Rev. B 65 245409
Google Scholar
[12] Cai K, Yin H, Qin Q H, Li Y 2014 Nano Lett. 14 2558
Google Scholar
[13] Servantie J, Gaspard P 2006 Phys. Rev. Lett. 97 13831
[14] Cook E H, Buehler M J, Spakovszky Z S 2013 J. Mech. Phys. Solids. 61 652
Google Scholar
[15] Zhao Y, Ma C C, Chen G, Jiang Q 2003 Phys. Rev. Lett. 91 175504
Google Scholar
[16] Guo W L, Guo Y F, Gao H J, Zheng Q S 2003 Phys. Rev. Lett. 91 125501
Google Scholar
[17] Kang J W, Lee J H 2008 Nanotechnology 19 285704
Google Scholar
[18] Liu P, Zhang Y W, Lu C 2005 J. Appl. Phys. 98 014301
Google Scholar
[19] Liu P, Zhang Y W, Lu C J 2006 Carbon 44 27
Google Scholar
[20] Chen L, Jiang W G, Zou H, Feng X Q, Qin Q H, Li X 2019 Phys. Lett. A. 383 2309
Google Scholar
[21] Lin Y W, Jiang W G, Qin Q H, Chen Y J 2019 Appl. Phys. Express. 12 065001
Google Scholar
[22] Voter A F, Doll J D 1984 J. Chem. Phys. 80 5832
Google Scholar
[23] Harrison J A, White C T, Colton R J, Brenner D W 1992 Phys. Rev. B. 46 9700
Google Scholar
[24] Brenner D W, Shenderove O A, Harrison J A, Stuart S J, Ni B, Sinnott S B 2002 J. Phys. Condens. Matter 14 783
Google Scholar
[25] Zou J, Ji B H, Feng X Q, Gao H J 2006 Small 2 1348
Google Scholar
[26] Doll J D 1982 J. Chem. Phys. 77 479
Google Scholar
[27] Lammps molecular dynamics simulator, http://lammps.sandia.gov, 2014 [2020-5-31]
[28] 邹航2019 硕士学位论文 (南昌: 南昌航空大学)
Zhou H 2019 M. S. Thesis (Nanchang: Nanchang Hangkong University) (in Chinese)
下载:
计量
- 文章访问数: 5118
- PDF下载量: 56
- 被引次数: 0
