-
CeRh2As2, as a recently discovered Ce-based 122-type heavy-fermion superconductor, has attracted much attention due to its non-Fermi-liquid behavior and two-phase superconductivity. The tetragonal crystal structure of CeRh2As2 maintains global centrosymmetry, which makes even-parity and odd-parity superconducting states different rather than mixed. The Ce site exhibits local inversion symmetry breaking, which results in staggered Rashba spin-orbit coupling. This may lead to the c axis field-induced transition between two superconducting phases and high critical field. Given the novel physics in CeRh2As2, including a possible quantum critical point and a spin-fluctuation-mediated superconducting pairing mechanism, the ultra-low-temperature electrical and thermal transport properties of CeRh2As2 under various magnetic fields are investigated in this work. The zero-field resistivity reveals a superconducting transition at the critical temperature Tc = 0.34 K. At a magnetic field of 1 T, a minimum resistivity appears near T0$ \approx $0.42 K, which may be due to partial gap opening caused by Fermi surface nesting, indicating that the system enters into a magnetically ordered state, which is not observed in zero field. In the temperature range from T0 to 2 K, the system exhibits non-Fermi-liquid behavior $ \rho\sim{{T}}^{0.44} $, indicating proximity to a quantum critical point. The superconducting transition is fully suppressed at 7 T, with resistivity recovering Fermi-liquid behavior at low temperature. No significant anomaly is observed in the zero-field thermal conductivity of CeRh2As2 near Tc. This absence of anomaly may be attributed to the high residual resistivity of the sample, and the reduction in carrier density during the superconducting transition and the T0 phase transition. It requires optimizing single crystal growth to reduce the effects of lattice defects or chemical disorder on thermal transport. Upon applying magnetic field, the thermal conductivity curve exhibits a small upward shift relative to its zero-field curve. At 0.15 K, thermal conductivity rises with the increase of magnetic field and is saturated at higher fields (above 5 T). In the normal state at 7 T, it is found that the electrical resistivity and thermal conductivity satisfy the Wiedemann-Franz law, indicating that the charge transfer and the heat transport are governed by the same quasiparticles, which is consistent with the Fermi-liquid behavior observed in resistivity under this field.
-
Keywords:
- heavy-fermion superconductor /
- CeRh2As2 /
- Electrical resistivity /
- ultra-low-temperature thermal conductivity
-
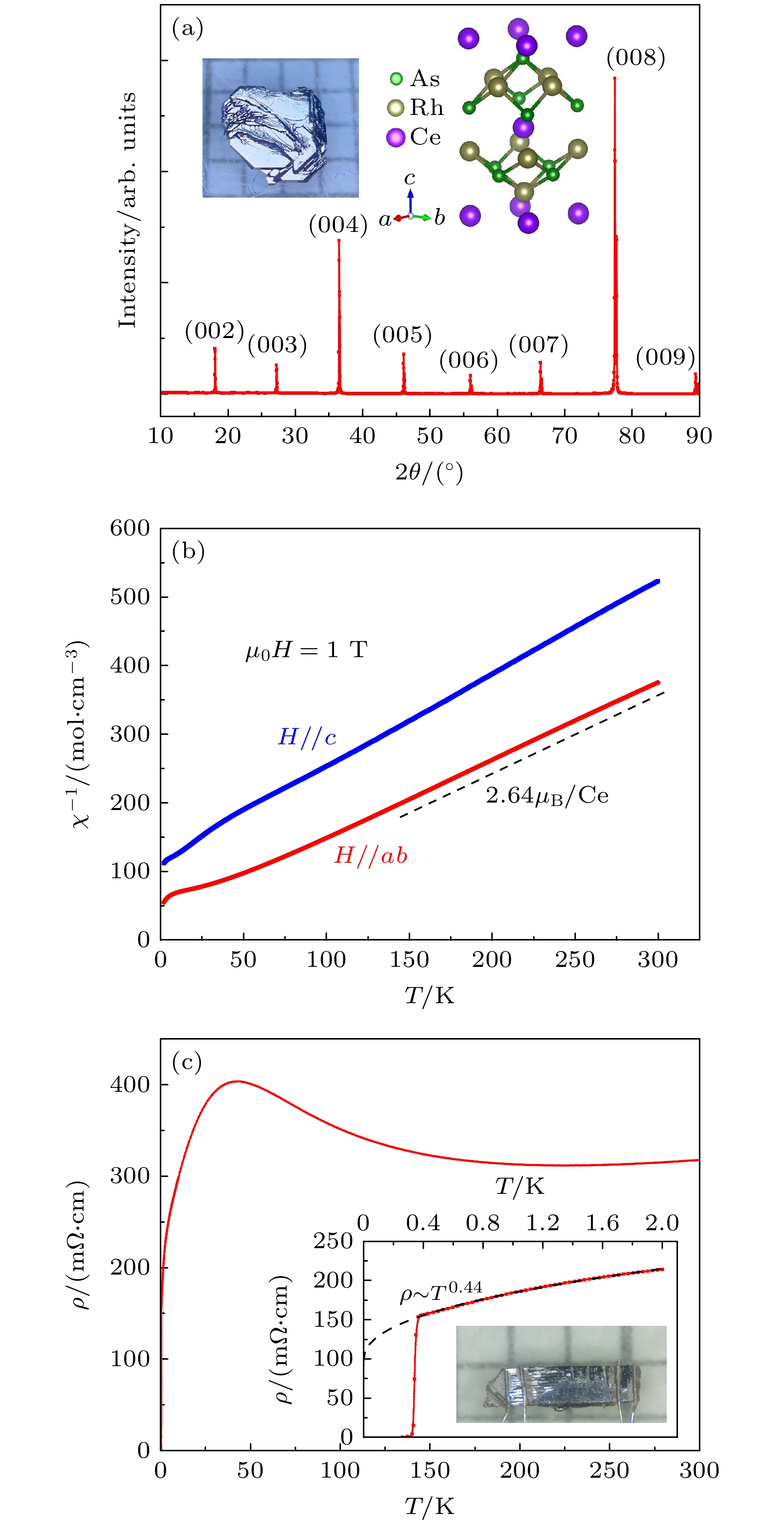
图 1 (a) CeRh2As2单晶的XRD谱, 插图为单晶的光学照片以及晶体结构示意图; (b) μ0H = 1 T下CeRh2As2单晶直流磁化率的倒数, 磁场方向分别沿ab面(红色)和晶体c轴(蓝色), 虚线斜率用于计算Ce3+的有效磁矩; (c) 零场下CeRh2As2单晶电阻率随温度变化, 插图为低于2 K的电阻率以及粘有4个电极的样品光学照片
Figure 1. (a) XRD pattern of CeRh2As2 single crystal, with the inset displaying the optical image of the single crystal and a schematic illustration of its crystal structure. (b) Reciprocal of the direct current magnetic susceptibility of CeRh2As2 single crystals at μ0H = 1 T, with magnetic field in the ab plane (red) and along the c axis (blue). The slope of the dashed line is used to calculate the effective magnetic moment of Ce3+. (c) Temperature dependence of the resistivity of CeRh2As2 single crystal in zero field. The inset displays the resistivity below 2 K along with an optical image of the sample with four electrodes.
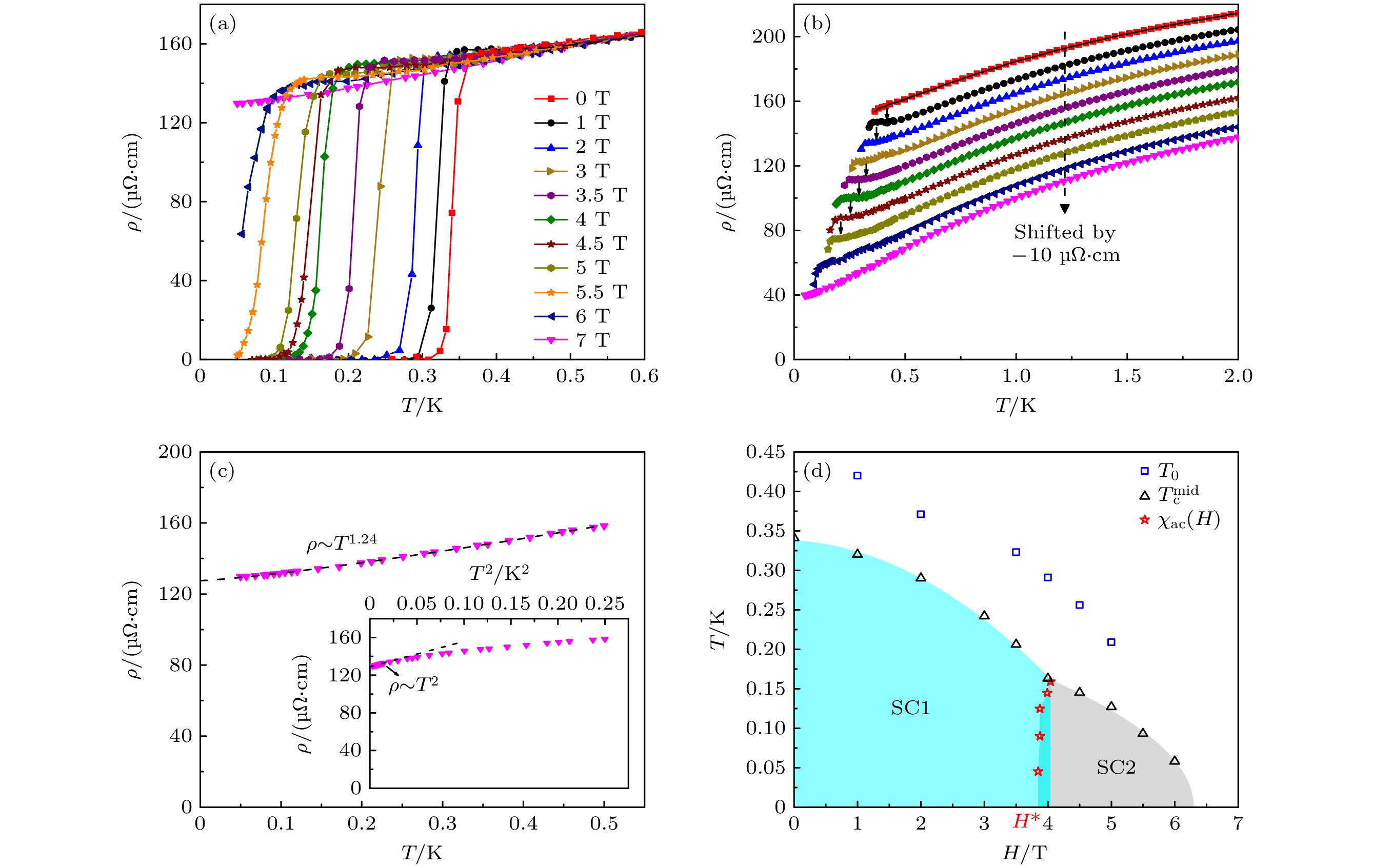
图 2 (a) CeRh2As2单晶在50 mK—0.6 K温区、不同磁场(最高到7 T)下的电阻率, 超导临界温度Tc随磁场增强逐渐降低, 并在7 T时被完全压制; (b) 不同磁场下, 温度低于2 K时的电阻率, 黑色小箭头指向T0异常, 随磁场增大, 电阻率在前一组数据偏移量的基础上偏移–10 μΩ, 虚线箭头指示偏移方向; (c) 主图为磁场7 T、温度低于0.5 K时的电阻率, 黑色虚线为$ \rho={\rho}_{0}+{A}{{T}}^{{\alpha}} $的拟合曲线, 插图中黑色虚线为温度低于0.15 K时, $ \rho $与T2的线性拟合结果; (d) CeRh2As2超导相图, 黑色上三角和蓝色正方形分别表示电阻率测量的超导临界温度$ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}} $与T0异常; 红色星形为交流磁化率测量结果, 数据来源于文献[10]
Figure 2. (a) Resistivity of CeRh2As2 single crystal measured between 50 mK and 0.6 K under various magnetic fields (up to 7 T). The superconducting critical temperature Tc decreases monotonically with increasing field and is fully suppressed at 7 T. (b) Resistivity below 2 K under various magnetic fields. Black arrows mark the T0 anomaly. Each successive curve is vertically offset by -10 μΩ relative to previous one, with dashed arrow indicating the offset direction. (c) Main panel: Resistivity at 7 T below 0.5 K. The black dashed curve represents the fit to $ \rho={\rho}_{0}+{A}{{T}}^{{\alpha}} $. Inset: Linear fit (black dashed line) to $ \rho({T}) $vs. T2 under 0.15 K; (d) Superconducting phase diagram of CeRh2As2. Black upward triangles and blue squares denote the $ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}} $ and T0 anomaly from resistivity measurements, respectively. Red stars are from AC magnetic susceptibility data reproduced from Ref.[10].
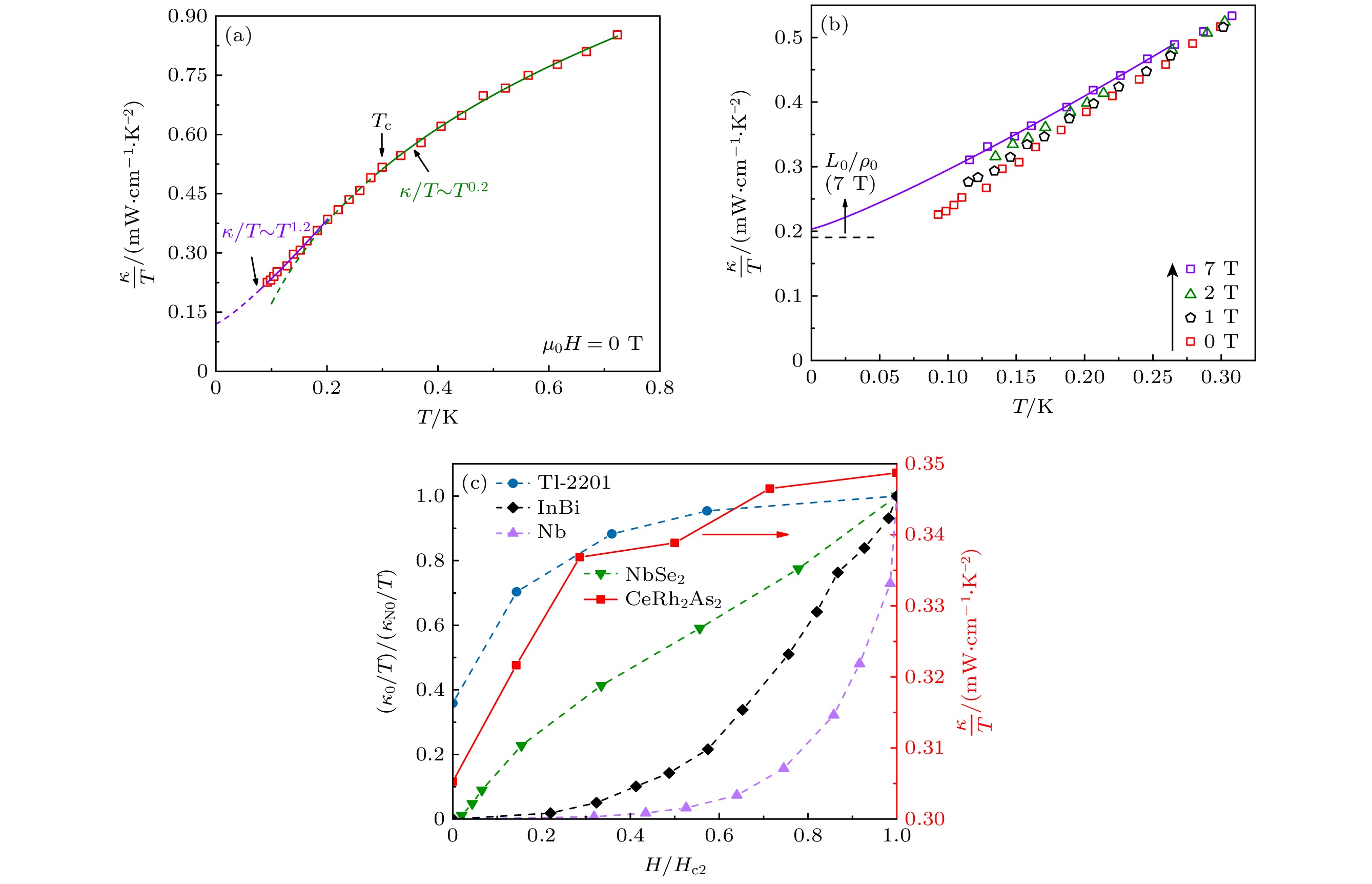
图 3 (a) 零场CeRh2As2单晶热导率的温度依赖, 黑色箭头指向超导临界温度Tc, 高于Tc和低于0.57Tc的拟合曲线分别为绿色和紫色, 并以虚线向更低温区延伸; (b) 加场(最高到7 T)下CeRh2As2单晶的极低温热导率, 黑色虚线为正常态Wiedemann-Franz定律的预期值$ {{L}}_{0}{/}{\rho}_{0}{(7 \;{\mathrm{T}})} $; (c)左轴为几种典型超导体的归一化剩余线性项κ0/T对归一化磁场强度H/Hc2的依赖关系, 右轴为CeRh2As2单晶在T = 0.15 K时κ/T的磁场依赖关系(红色方形)
Figure 3. (a) Temperature dependence of the zero-field thermal conductivity of CeRh2As2 single crystal, with the black arrow indicating the superconducting critical temperature Tc. The fitting curves above Tc and below 0.57Tc are green and purple, respectively, and are extended to lower temperatures with dashed lines. (b) Low-temperature thermal conductivity of CeRh2As2 single crystal under applied fields (up to 7 T), with the black dashed line representing the normal-state Wiedemann-Franz law expectation $ {{L}}_{0}{/}{\rho}_{0}{(7 \; {\mathrm{T}})} $. (c) Left axis: Magnetic field dependence of the normalized residual linear term κ0/T versus normalized magnetic field strength H/Hc2 for several typical superconductors; Right axis: Magnetic field dependence of κ/T for the CeRh2As2 single crystal at T = 0.15 K (red squares).
-
[1] Norman M R 2011 Science 332 196
Google Scholar
[2] 李宇, 盛玉韬, 杨义峰 2021 70 017402
Google Scholar
Li Y, Sheng Y T, Yang Y F 2021 Acta. Phys. Sin. 70 017402
Google Scholar
[3] Steglich F, Aarts J, Bredl C D, Lieke W, Meschede D, Franz W, Schafer H 1979 Phys. Rev. Lett. 43 1892
Google Scholar
[4] Smidman M, Stockert O, Nica E M, Liu Y, Yuan H Q, Si Q M, Steglich F 2023 Rev. Mod. Phys. 95 031002
Google Scholar
[5] Grosche F, Julian S, Mathur N, Lonzarich G 1996 Physica B 223 50
Google Scholar
[6] Araki S, Nakashima M, Settai R, Kobayashi T C, Onuki Y 2002 J. Phys. Condens. Matter 14 L377
Google Scholar
[7] Yuan H Q, Grosche F M, Deppe M, Geibel C, Sparn G, Steglich F 2003 Science 302 2104
Google Scholar
[8] Grosche F, Walker I, Julian S, Mathur N, Freye D, Steiner M, Lonzarich G 2001 J. Phys. Condens. Matter 13 2845
Google Scholar
[9] 谢武, 沈斌, 张勇军, 郭春煜, 许嘉诚, 路欣, 袁辉球 2019 68 177101
Google Scholar
Xie W, Shen B, Zhang Y J, Guo C Y, Xu J C, Lu X, Yuan H Q 2019 Acta. Phys. Sin. 68 177101
Google Scholar
[10] Khim S, Landaeta J F, Banda J, Bannor N, Brando M, Brydon P M R, Hafner D, Küchler R, Cardoso-Gil R, Stockert U, Mackenzie A P, Agterberg D F, Geibel C, Hassinger E 2021 Science 373 1012
Google Scholar
[11] Chajewski G, Kaczorowski D 2024 Phys. Rev. Lett. 132 076504
Google Scholar
[12] Hafner D, Khanenko P, Eljaouhari E O, Küchler R, Banda J, Bannor N, Lühmann T, Landaeta J F, Mishra S, Sheikin I, Hassinger E, Khim S, Geibel C, Zwicknagl G, Brando M 2022 Phys. Rev. X 12 011023
[13] Khim S, Stockert O, Brando M, Geibel C, Baines C, Hicken T J, Luetkens H, Das D, Shiroka T, Guguchia Z, Scheuermann R 2025 Phys. Rev. B 111 115134
Google Scholar
[14] Schmidt B, Thalmeier P 2024 Phys. Rev. B 110 075154
Google Scholar
[15] Steppke A, Küchler R, Lausberg S, Lengyel E, Steinke L, Borth R, Lühmann T, Krellner C, Nicklas M, Geibel C 2013 Science 339 933
Google Scholar
[16] Movshovich R, Jaime M, Thompson J D, Petrovic C, Fisk Z, Pagliuso P G, Sarrao J L 2001 Phys. Rev. Lett. 86 5152
Google Scholar
[17] Metz T, Bae S, Ran S, Liu I L, Eo Y S, Fuhrman W T, Agterberg D F, Anlage S M, Butch N P, Paglione J 2019 Phys. Rev. B 100 220504
Google Scholar
[18] Villegas H A V 2013 Ph. D. Dissertation (Dresden: Dresden University of Technology
[19] Chajewski G, Szymanski D, Daszkiewicz M, Kaczorowski D 2024 Mater. Horiz. 11 855
Google Scholar
[20] Onishi S, Stockert U, Khim S, Banda J, Brando M, Hassinger E 2022 Front. Electron. Mater 2 880579
Google Scholar
[21] Khanenko P, Hafner D, Semeniuk K, Banda J, Lühmann T, Bärtl F, Kotte T, Wosnitza J, Zwicknagl G, Geibel C, Landaeta J F, Khim S, Hassinger E, Brando M 2025 Phys. Rev. B 111 045162
Google Scholar
[22] Mishra S, Liu Y, Bauer E D, Ronning F, Thomas S M 2022 Phys. Rev. B 106 L140502
Google Scholar
[23] Hamann S, Zhang J, Jang D, Hannaske A, Steinke L, Lausberg S, Pedrero L, Klingner C, Baenitz M, Steglich F, Krellner C, Geibel C, Brando M 2019 Phys. Rev. Lett. 122 077202
Google Scholar
[24] Gruner T, Jang D, Huesges Z, Cardoso-Gil R, Fecher G H, Koza M M, Stockert O, Mackenzie A P, Brando M, Geibel C 2017 Nat. Phys. 13 967
Google Scholar
[25] Wu Y, Zhang Y J, Ju S L, Hu Y, Huang Y E, Zhang Y N, Zhang H L, Zheng H, Yang G W, Eljaouhari E O, Song B P, Plumb N C, Steglich F, Shi M, Zwicknagl G, Cao C, Yuan H Q, Liu Y 2024 Chin. Phys. Lett. 41 097403
Google Scholar
[26] Chen T, Siddiquee H, Xu Q Z, Rehfuss Z, Gao S Y, Lygouras C, Drouin J, Morano V, Avers K E, Schmitt C J, Podlesnyak A, Paglione J, Ran S, Song Y, Broholm C 2024 Phys. Rev. Lett. 133 266505
Google Scholar
[27] Weng Z F, Smidman M, Jiao L, Lu X, Yuan H Q 2016 Rep. Prog. Phys. 79 094503
Google Scholar
[28] Doniach S 1977 Physica B+C 91 231
Google Scholar
[29] Coleman P, Schofield A J 2005 Nature 433 226
Google Scholar
[30] Li S Y, Bonnemaison J B, Payeur A, Fournier P, Wang C H, Chen X H, Taillefer L 2008 Phys. Rev. B 77 134501
Google Scholar
[31] Sutherland M, Hawthorn D G, Hill R W, Ronning F, Wakimoto S, Zhang H, Proust C, Boaknin E, Lupien C, Taillefer L, Liang R, Bonn D A, Hardy W N, Gagnon R, Hussey N E, Kimura T, Nohara M, Takagi H 2003 Phys. Rev. B 67 174520
Google Scholar
[32] Cohn J L, Skelton E F, Wolf S A, Liu J Z, Shelton R N 1992 Phys. Rev. B 45 13144
Google Scholar
[33] Yu R C, Salamon M B, Lu J P, Lee W C 1992 Phys. Rev. Lett. 69 1431
Google Scholar
[34] Landaeta J F, León A M, Zwickel S, Lühmann T, Brando M, Geibel C, Eljaouhari E O, Rosner H, Zwicknagl G, Hassinger E, Khim S 2022 Phys. Rev. B 106 014506
[35] Lowell J, Sousa J B 1970 J. Low Temp. Phys. 3 65
Google Scholar
[36] Willis J O, Ginsberg D M 1976 Phys. Rev. B 14 1916
Google Scholar
[37] Boaknin E, Tanatar M A, Paglione J, Hawthorn D, Ronning F, Hill R W, Sutherland M, Taillefer L, Sonier J, Hayden S M, Brill J W 2003 Phys. Rev. Lett. 90 117003
Google Scholar
[38] Proust C, Boaknin E, Hill R W, Taillefer L, Mackenzie A P 2002 Phys. Rev. Lett. 89 147003
Google Scholar
DownLoad:
Metrics
- Abstract views: 216
- PDF Downloads: 10
- Cited By: 0
