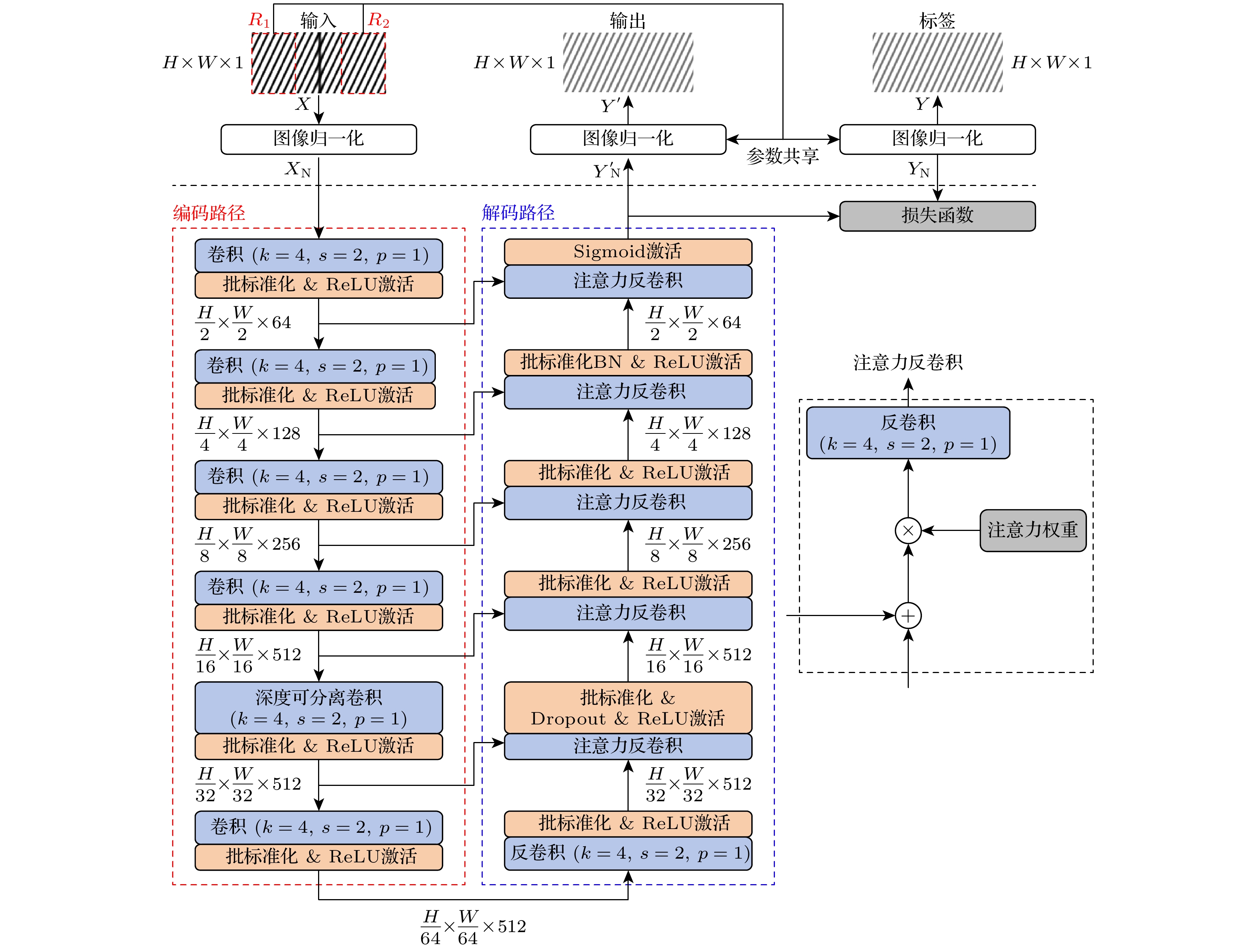
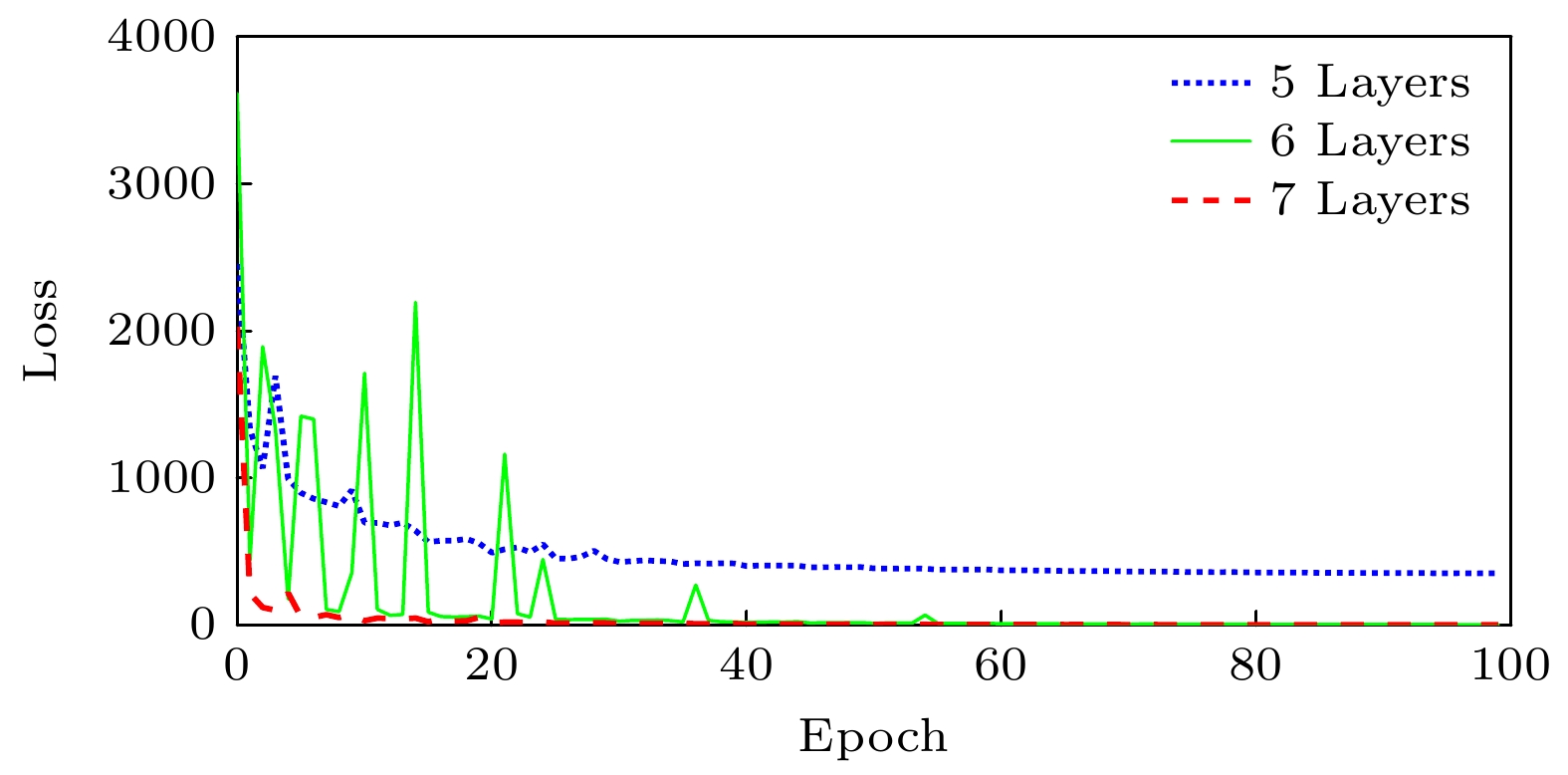
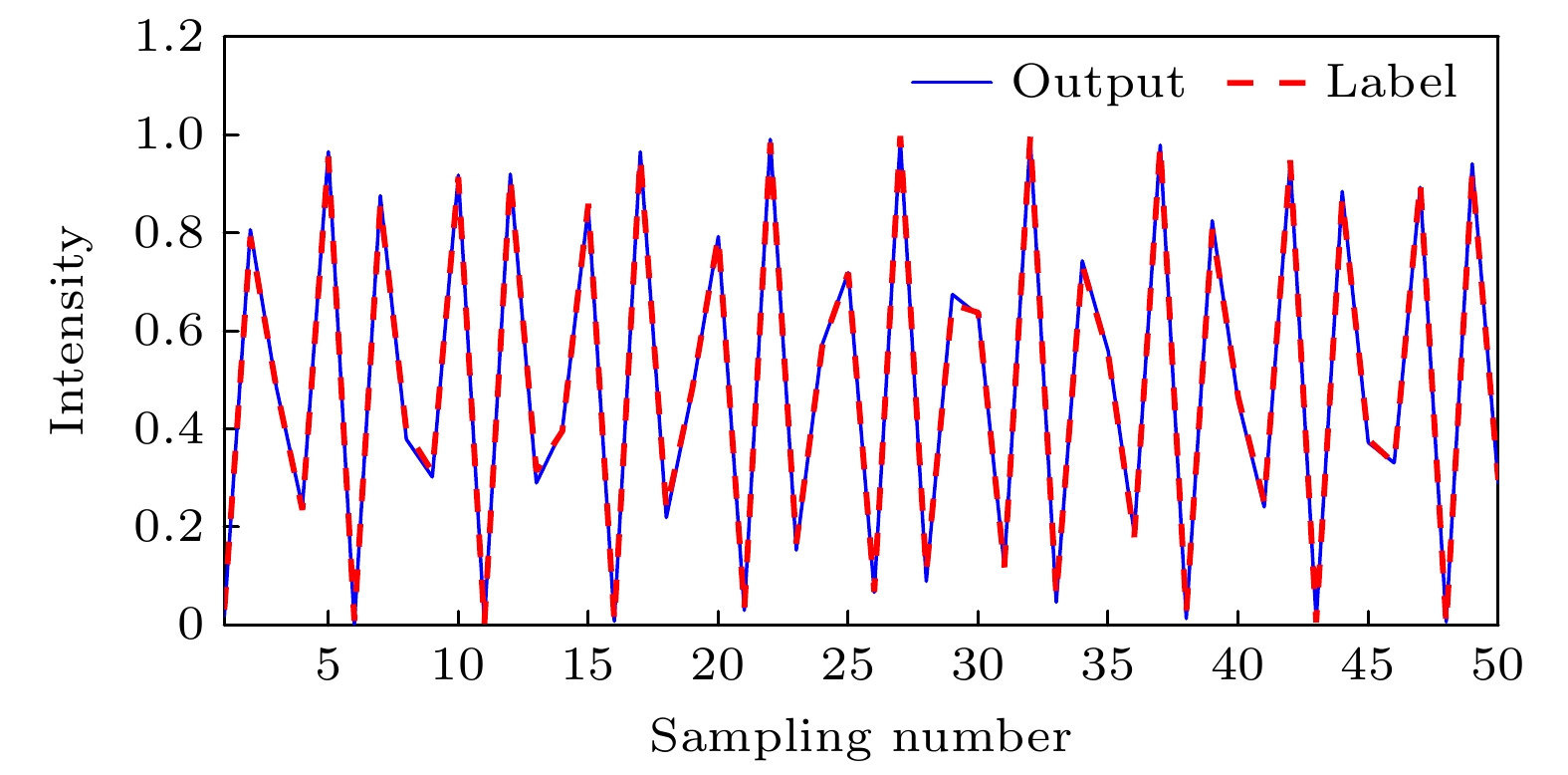
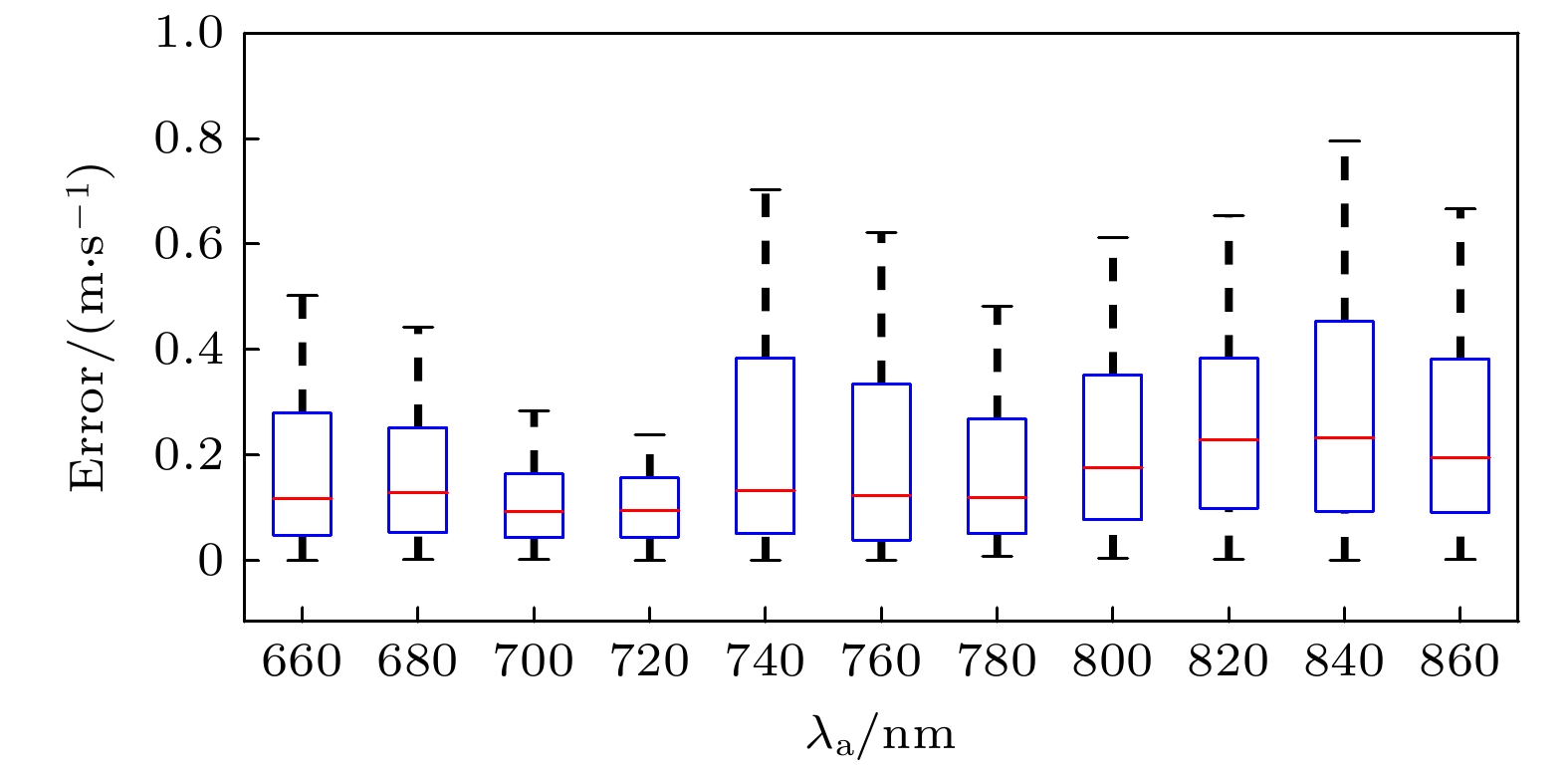
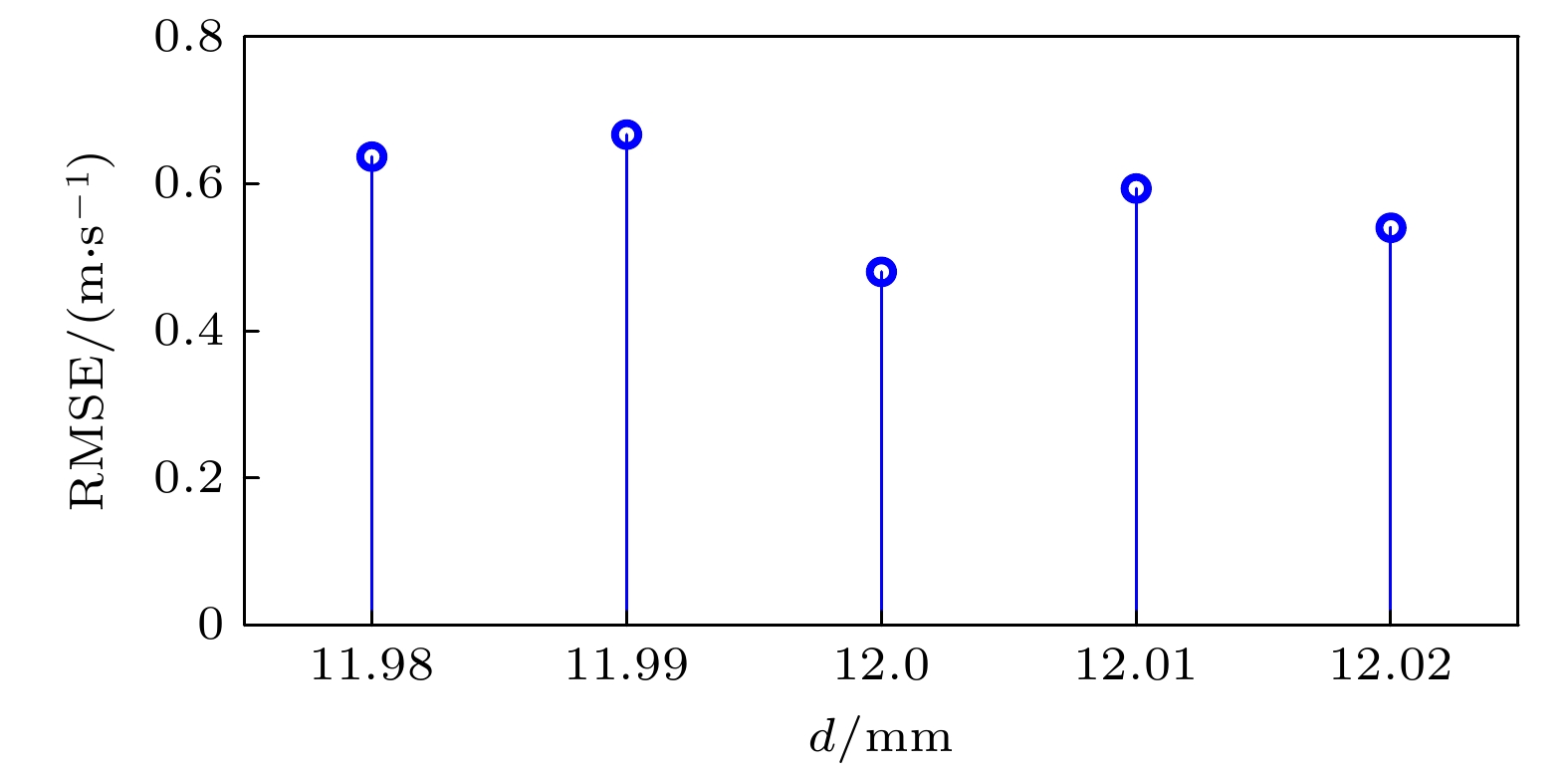
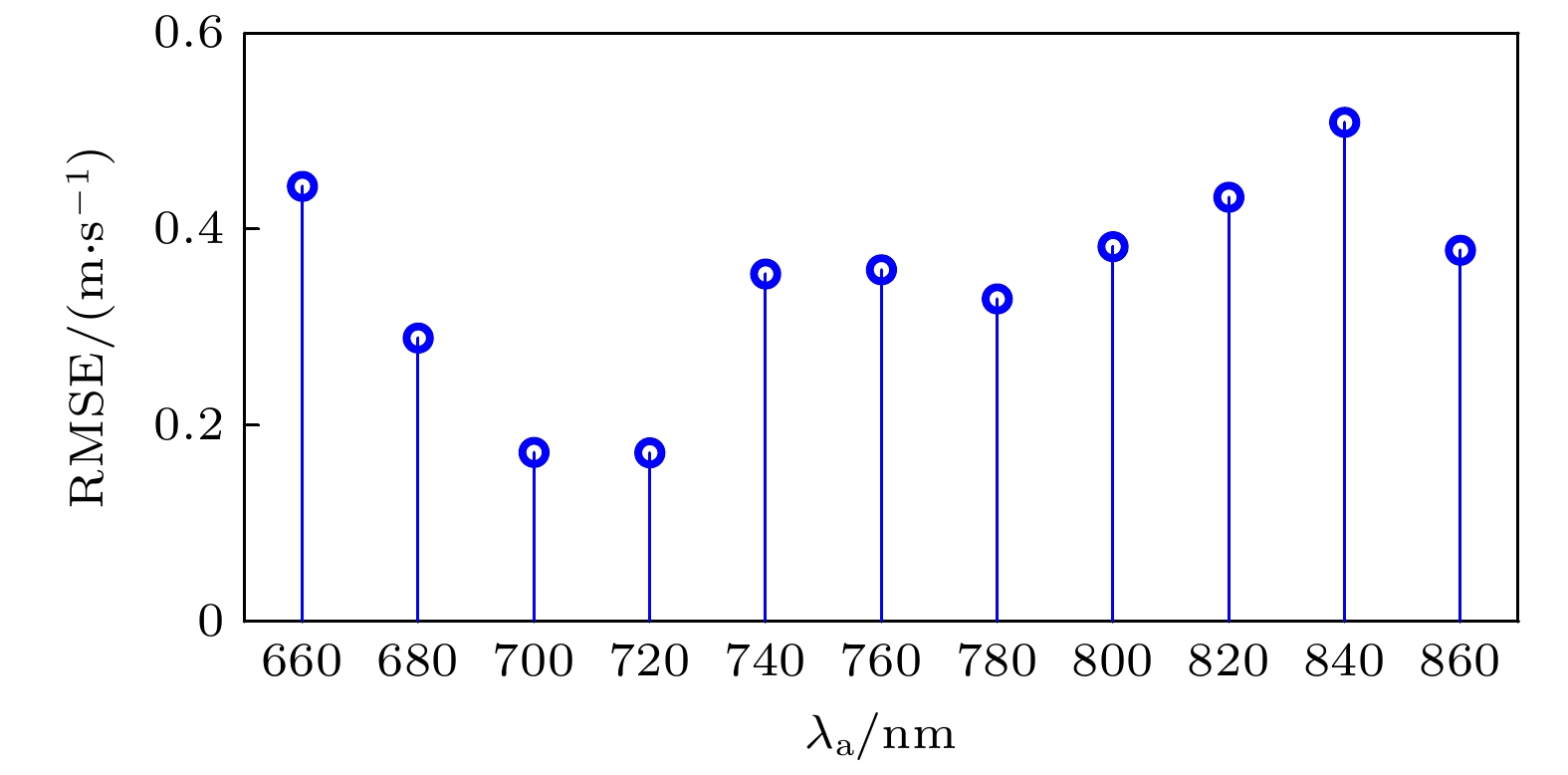
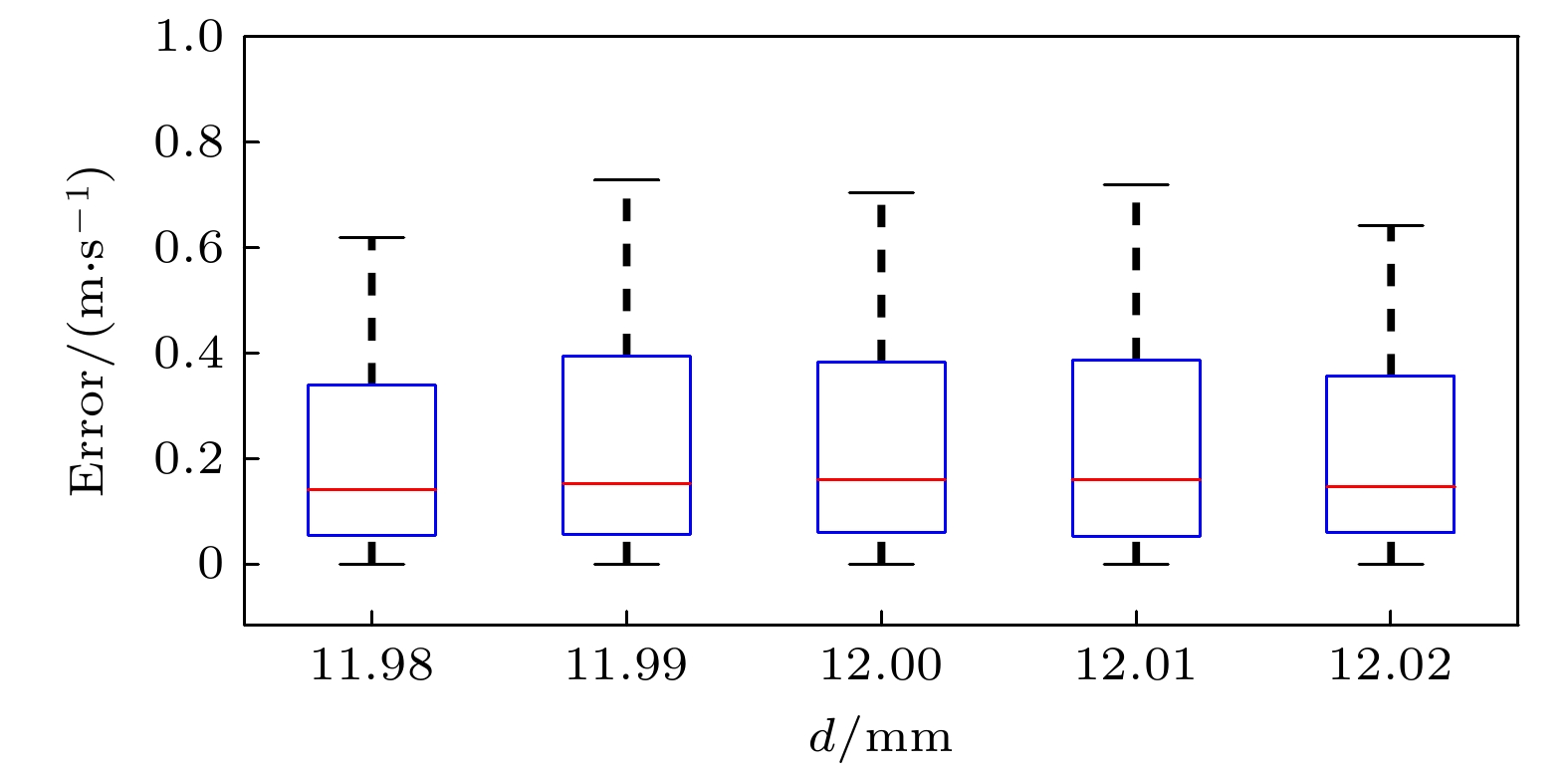
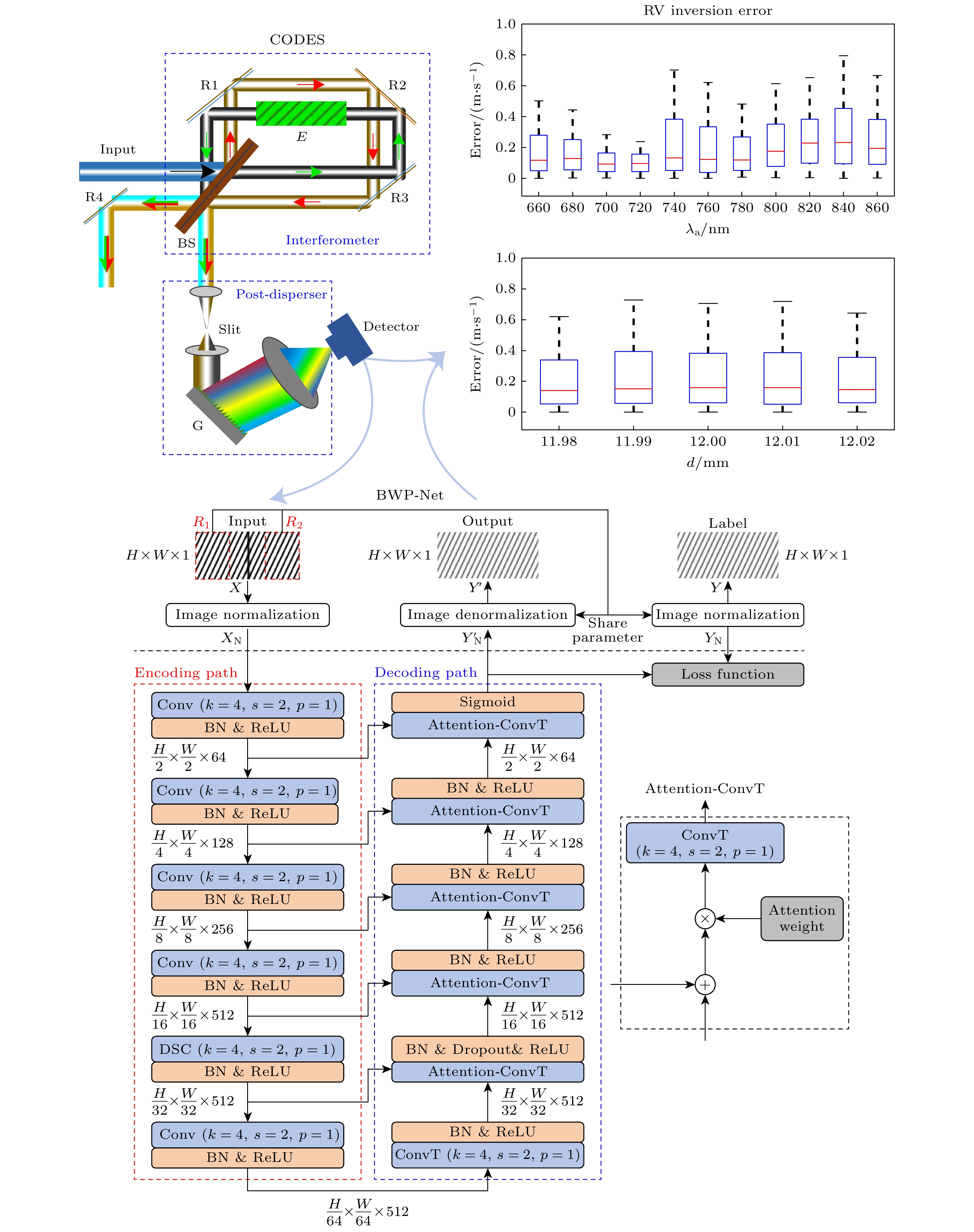
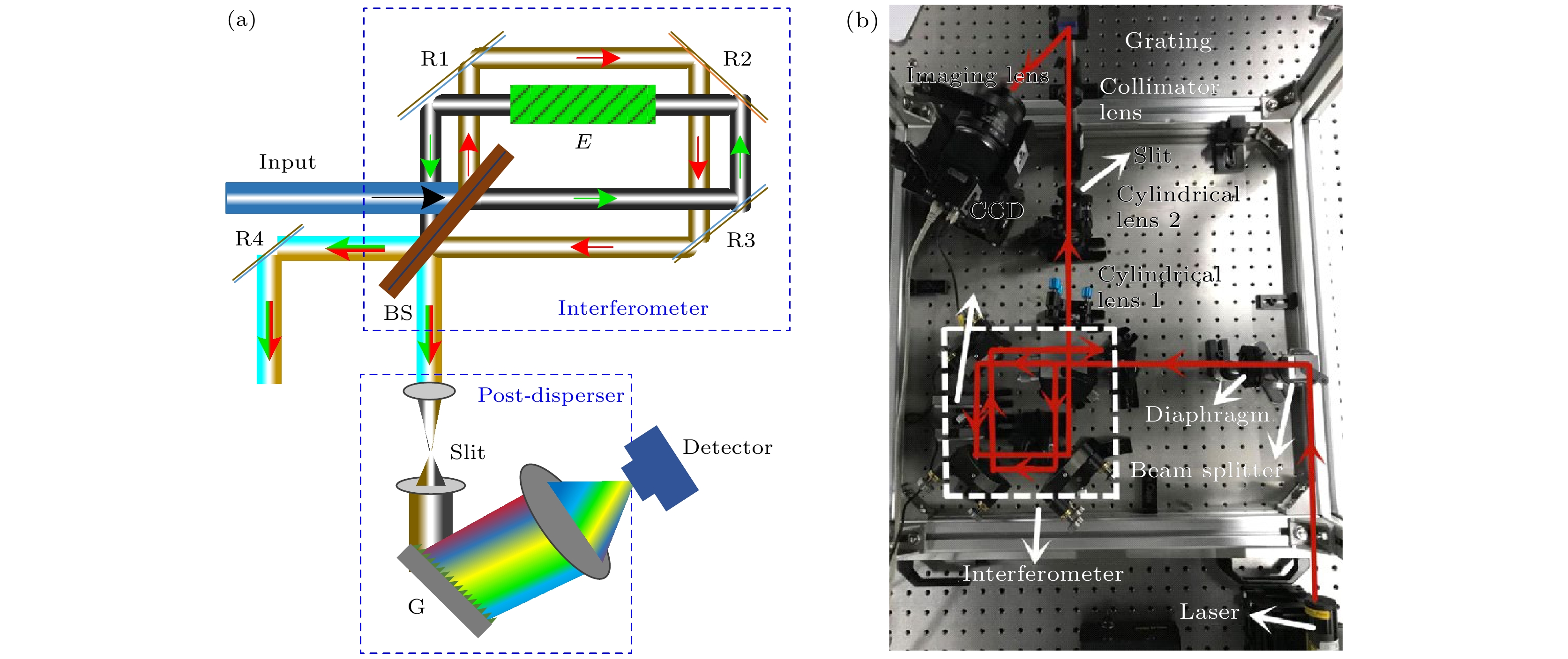
-
Coherent-dispersion spectrometer (CODES) is an exoplanet detection instrument based on the radial velocity (RV) method. It detects changes in RV by measuring the Doppler phase shift of the interference spectrum of stellar absorption line. However, the background white light in the stellar absorption spectrum disturbs the phase analysis of CODES, which leads to phase error and seriously affects the accuracy of RV inversion. The larger the cosine amplitude of the background white light, the greater the error is. In order to effectively remove background white light and correct Doppler phase shift, a background white light prediction network (BWP-Net) is proposed based on the U-Net architecture by utilizing the principle and data characteristics of CODES in this study. To accelerate the convergence of the BWP-Net model, the interference spectrum of absorption line from CODES and the ideal interference spectrum of background white light are used as inputs and labels for the model after image normalization, while the model output becomes the predicted interference spectrum of background white light after inverse normalization. The BWP-Net consists of symmetric 6-layer encoding path and decoding path. First, in the encoding path, different levels of features are extracted step by step from the interference spectrum of stellar absorption line through combination of multi-channel convolution and depthwise separable convolution, extracting features effectively while reducing computational costs reasonably. In each convolution layer, spatial downsampling is performed through convolution with a stride of 2 and the number of feature channels is increased until the fourth layer, thus various features, from simple to abstract, local to global, are extracted for the preparation of image reconstruction in the decoding path. Second, in the decoding path, the image details are gradually reconstructed from the features extracted through several layers of attention transposed-convolution. In each layer of attention transposed-convolution, spatial upsampling is performed based on the fusion of shallow features and deep features through matrix addition and the number of feature channels are reduced, at the same time attention of different levels is paid to the features through a learnable weight matrix, so as to suppress the absorption line information gradually during image reconstruction. At the last layer of the decoding path, the sigmoid activation function is used to control the model output in the 0-1 interval, making it easier to denormalize. Finally, a region weighted loss function that combines mean-square error and multi-scale structural similarity is used for training so as to consider pixel level differences and structural similarity between the model output and the labels, while enhancing the suppression of absorption lines in the central region of the interference spectrum through region weighting. And the output of BWP-Net is the prediction of the interference spectrum of background white light, which is subtracted from the interference spectrum of stellar absorption lines for phase analysis. The experimental results show that under different absorption lines, different fixed optical path differences, and different RVs, after removing background white light from the output of BWP-Net, the RV inversion error is less than 1 m/s, mainly concentrated in the region of 0–0.4 m/s, with an average error of 0.2353 m/s and a root mean square error of 0.3769 m/s. And the distribution of RV inversion error is relatively uniform under different parameter conditions, the median error is less than 0.25 m/s at different absorption line wavelengths, and less than 0.2 m/s at different fixed optical path differences. Thes indicate that BWP-Net not only predicts background white light accurately, but also has good stability and robustness, providing strong support for high-precision and stable RV inversion for CODES.
-
Keywords:
- radial velocity /
- Doppler phase shift /
- background white light prediction /
- convolutional neural network
-
图 1 CODES (a)工作原理 (b)实验装置
Figure 1. CODES: (a) Schematic diagram; (b) experimental setup.
图 2 S1int的余弦振幅
Figure 2. Cosine amplitude of S1int.
图 3 背景白光预测网络架构
Figure 3. Background White light prediction network (BWP-Net) architecture.
图 4 不同层数模型损失对比结果
Figure 4. Comparison result of loss between models with different layers.
图 5 吸收线干涉光谱
Figure 5. Interference spectrum of absorption line.
图 6 背景白光干涉光谱
Figure 6. Interference spectrum of background white light.
图 7 BWP-Net模型输出与标签对比
Figure 7. Comparison of BWP-Net output and label.
图 8 不同λa下视向速度误差分布
Figure 8. Distribution of radial velocity error with different λa.
图 11 不同t下视向速度均方根误差
Figure 11. RMSE of radial velocity error with different t.
图 9 不同λa下视向速度均方根误差
Figure 9. RMSE of radial velocity error with different λa.
图 10 不同t下视向速度误差分布
Figure 10. Distribution of radial velocity error with different t.
图 12 特征和参数可视化 (a)编码路径特征; (b)解码路径特征; (c)注意力权重
Figure 12. Visualization of features and parameters: (a) Encoder features; (b) decoder features; (c) attention weight.
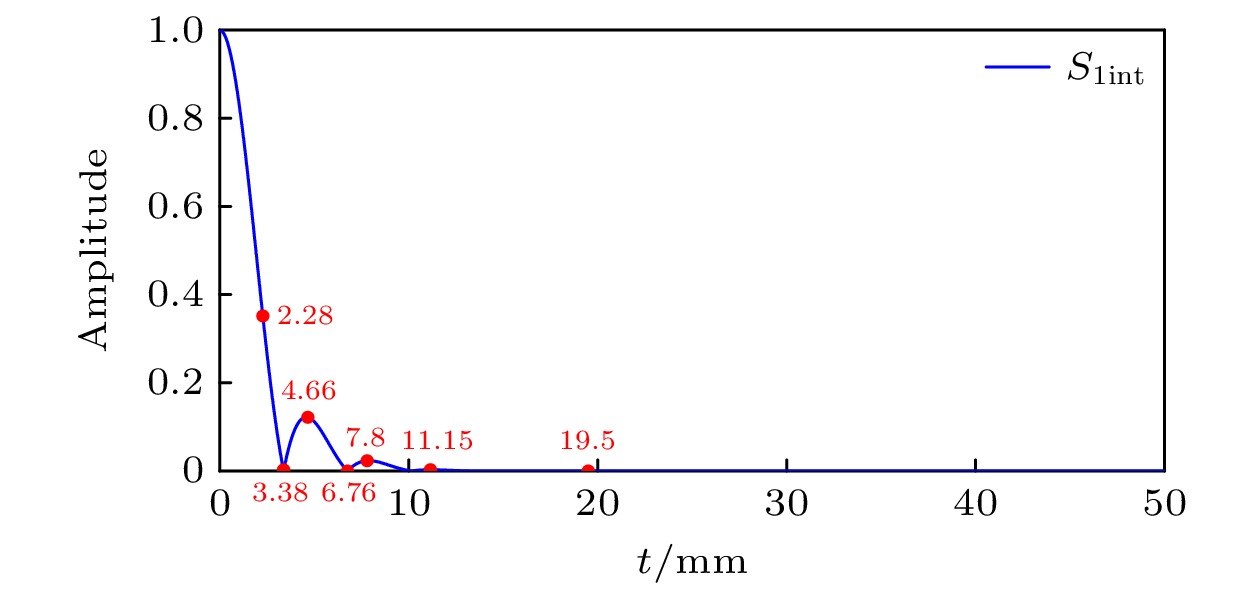
表 1 v1 = 0 m/s, v2 = 1000 m/s时, 不同光程差下相位差解析结果
Table 1. Phase shift with different OPD at v1 = 0 m/s and v2 = 1000 m/s.
t/mm ΔΦ/rad ΔΦabsorb/rad Δvabsorb/(m·s–1) ΔΦemission/rad Δvemission/(m·s–1) 2.28 0.0195π 1.9878π 10200.42 0.0195π 999.69 3.37 0.0288π 0.0292π 1012.25 0.0288π 999.68 3.38 0.0289π 0.0287π 991.86 0.0289π 999.68 3.39 0.0290π 0.0282π 972.48 0.0290π 999.69 4.66 0.0398π 0.0183π 458.45 0.0398π 999.69 6.76 0.0578π 0.0579π 1001.50 0.0578π 999.70 7.80 0.0667π 0.0880π 1319.80 0.0666π 999.71 11.15 0.0953π 0.0916π 960.96 0.0953π 999.75 19.50 0.1667π 0.1666π 999.82 0.1666π 999.87 
DownLoad: CSV
表 2 测试集部分数据分析结果
Table 2. Analysis results of partial data in the test set.
λa/nm Δλa/nm A t/mm v1/(m·s–1) v2(/m·s–1) Δvt/(m·s–1) Error/(m·s–1) 710 0.02 0.9 11.98 1800 1900 99.9991 0.0009 730 0.03 0.9 12.00 1300 1500 199.9988 0.0012 740 0.02 0.9 12.01 1500 1700 200.0006 0.0006 820 0.03 0.9 12.02 1600 1900 300.0036 0.0036 750 0.02 0.8 12.02 1000 1400 400.0034 0.0034 780 0.03 0.7 12.02 1200 1700 499.9901 0.0099 860 0.02 0.9 12.00 1000 1600 599.9952 0.0048 760 0.02 0.9 11.98 1300 2000 699.9988 0.0012 770 0.02 0.7 11.99 0 800 799.7536 0.2464 870 0.02 0.9 11.99 1100 2000 899.9507 0.0493 830 0.03 0.7 12.01 100 1100 999.8383 0.1617 690 0.02 0.8 12.01 0 1100 1099.8283 0.1717 800 0.03 0.8 12.00 0 1700 1699.7822 0.2178 850 0.03 0.9 11.98 0 1200 1200.0631 0.0631 790 0.03 0.7 12.02 100 1400 1299.8981 0.1019 720 0.02 0.8 12.01 100 1500 1400.0173 0.0173 660 0.02 0.8 11.98 0 1500 1499.9827 0.0173 670 0.03 0.8 12.02 100 1700 1600.3113 0.3113 840 0.03 0.9 11.98 100 1800 1700.1090 0.1090 700 0.02 0.9 12.01 100 1900 1800.1403 0.1403 810 0.03 0.9 12.02 0 1900 1900.0923 0.0923 680 0.02 0.7 12.01 0 2000 2000.4200 0.4200
DownLoad: CSV
-
[1] Bailey I J, Mateo M, White J R, Shectman A S, Crane D J 2018 MNRAS 475 1609
Google Scholar
[2] Vanzi L, Zapata A, Flores M, Brahm R, Pinto T M, Rukdee S, Jones M, Ropert S, Shen T, Ramirez S, Suc V, Jordán A, Espinoza N 2018 MNRAS 477 5041
Google Scholar
[3] Mamajek E E, Burgasser J A 2025 Appita J. 169 77
[4] Laliotis K, Burt A J, Mamajek E E, Li Z, Perdelwitz V, Zhao J, Butler P R, Holden B, Rosenthal L, Fulton J B, Feng F, Kane R S, Bailey J, Carter B, Crane D J, Furlan E , Gnilka L C, Howell B S, Laughlin G, Shectman A S, Teske K J, Tinney G C, Vogt S S, Wang X S, Wittenmyer A R 2023 Appita J. 165 176
[5] The Extrasolar Planets Encyclopedia [2025-1-17]
[6] Wang X, Chang L, Wang L, Ji H, Xian H, Tang Z, Xin Y, Wang C, He S, Zhang J, Lun B, Wei K, Li X, Jiang X, Wang H, Li H, Mao J 2020 Res. Astron. Astrophys. 20 032
Google Scholar
[7] Xiao G, Teng H, Zhou J, Sato B, Liu Y, Bi S, Takarada T, Kuzuhara M, Hon M, Wang L, Omiya M, Harakawa H, Zhao F, Zhao G, Kambe E, Izumiura H, Ando H, Noguchi K, Wang W, Zhai M, Song N, Yang C, Li T, Brandt D T, Yoshida M, Yoichi Itoh, Kokubo E 2024 Appita J. 167 59
[8] Luo X, Gu S, Xiang Y, Cameron A C, Kim K, Han I, Lee B 2022 Appita J. 163 287
[9] Wang C, Bai J, Fan Y, Mao J, Chang L, Xin Y, Zhang J, Lun B, Wang J, Zhang X, Ying M, Lu K, Wang X, Ji K, Xiong D, Yu X, Ding X, Ye K, Xing L, Yi W, Xu L, Zheng X, Feng Y, He S, Wang X, Liu Z, Chen D, Xu J, Qin S, Zhang R, Tan H, Li Z, Lou K, Li J, Liu W 2019 Res. Astron. Astrophys. 19 149
Google Scholar
[10] Grieves N, Ge J, Thomas N, Ma B, Sithajan S, Ghezzi L, Kimock B, Willis K, Lee D N, Brian Lee, Fleming W S, Agol E, Troup N, Paegert M, Schneider P D, Stassun K, Varosi F, Zhao B, Jian L, Li R, Mello P F G, Bizyaev D, Pan K, Dutra-Ferreira L, Lorenzo-Oliveira D, Santiago X B, Costa N L, Maia G A M, Ogando C L R, Peloso F E 2017 MNRAS 467 4264
Google Scholar
[11] Grieves N, Ge J, Thomas N, Willis K, Ma B, Lorenzo-Oliveira D, Queiroz A B A, Ghezzi L, Chiappini C, Anders F, Dutra-Ferreira L, Mello P F G, Santiago X B, Costa N L, Ogando C L R, Peloso F E, Tan C J, Schneider P D, Pepper J, Stassun G K, Zhao B, Bizyaev D, Pan K 2018 MNRAS 481 3244
Google Scholar
[12] Wei R Y, Chen S S, Hu B L, Yan Q Q, Wu Y H, Wang P C 2020 Publ. Astron. Soc. Pac. 132 015003
Google Scholar
[13] Chen S, Wei R, Xie Z, Wu Y, Di L, Wang F, Zhai Y 2021 Appl. Opt. 60 4535
Google Scholar
[14] Guan S, Liu B, Chen S, Wu Y, Wang F, Liu X, Wei R 2024 Sci. Rep. 14 17445
Google Scholar
[15] Wu Y, Chen S, Wang P, Zhou S, Feng Y, Zhang W, Wei R 2021 MNRAS 503 3032
Google Scholar
[16] Guan S, Liu B, Chen S, Wu Y, Wang F, Wang S, Liu X, Wei R 2024 Opt. Commun. 561 130443
Google Scholar
[17] 周静, 张晓芳, 赵延庚 2021 70 054201
Google Scholar
Zhou J, Zhang X F, Zhao Y G 2021 Acta Phys. Sin. 70 054201
Google Scholar
[18] 朱琦, 许多, 张元军, 李玉娟, 王文, 张海燕 2022 71 244301
Google Scholar
Zhu Q, Xu D, Zhang Y J, Li Y J, Wang W, Zhang H Y 2022 Acta Phys. Sin. 71 244301
Google Scholar
[19] Long J, Shelhamer E, Darrell T 2015 arXiv: 1411.4038v2 [cs. CV]
[20] Roy S K, Krishna G, Dubey S R, Chaudhuri B B 2020 IEEE Geosci. Remote Sens. Lett. 17 277
Google Scholar
[21] Ronneberger O, Fischer P, Brox T 2015 Medical Image Computing and Computer -Assisted Intervention Munich, Germany, October 5—9, 2015 p234
[22] Nehaa F, Bhatia D, Shuklab K D, Dalvia M S, Mantzouc N, Shubbar S 2024 arXiv: 2412.02242v1 [eess. IV]
[23] Siddique N, Sidike P, Elkin C, Devabhaktuni V 2020 arXiv: 2011.01118 [eess. IV]
[24] Isola P, Zhu J, Zhou T, Efros A A 2018 arXiv: 1611.07004v3 [cs. CV]
[25] Basu A, Mondal R, Bhowmik S, Sarkara R 2020 J. Electron. Imaging 29 063019
[26] Hu Y, Tang Z, Hu J, Lu X, Zhang W, Xie Z, Zuo H, Li L, Huang Y 2023 Opt. Commun. 540 129488
Google Scholar
DownLoad:
Metrics
- Abstract views: 307
- PDF Downloads: 8
- Cited By: 0
