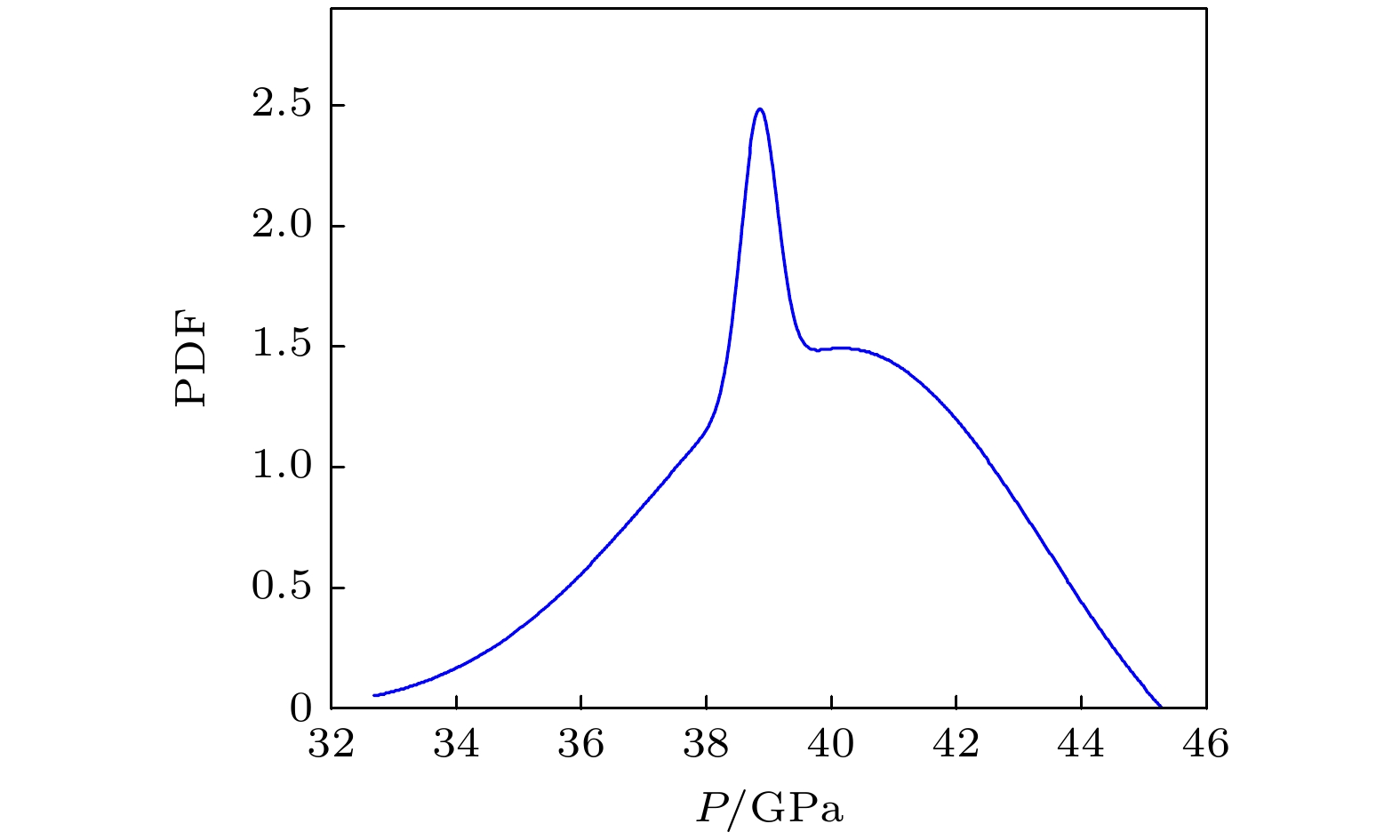
-
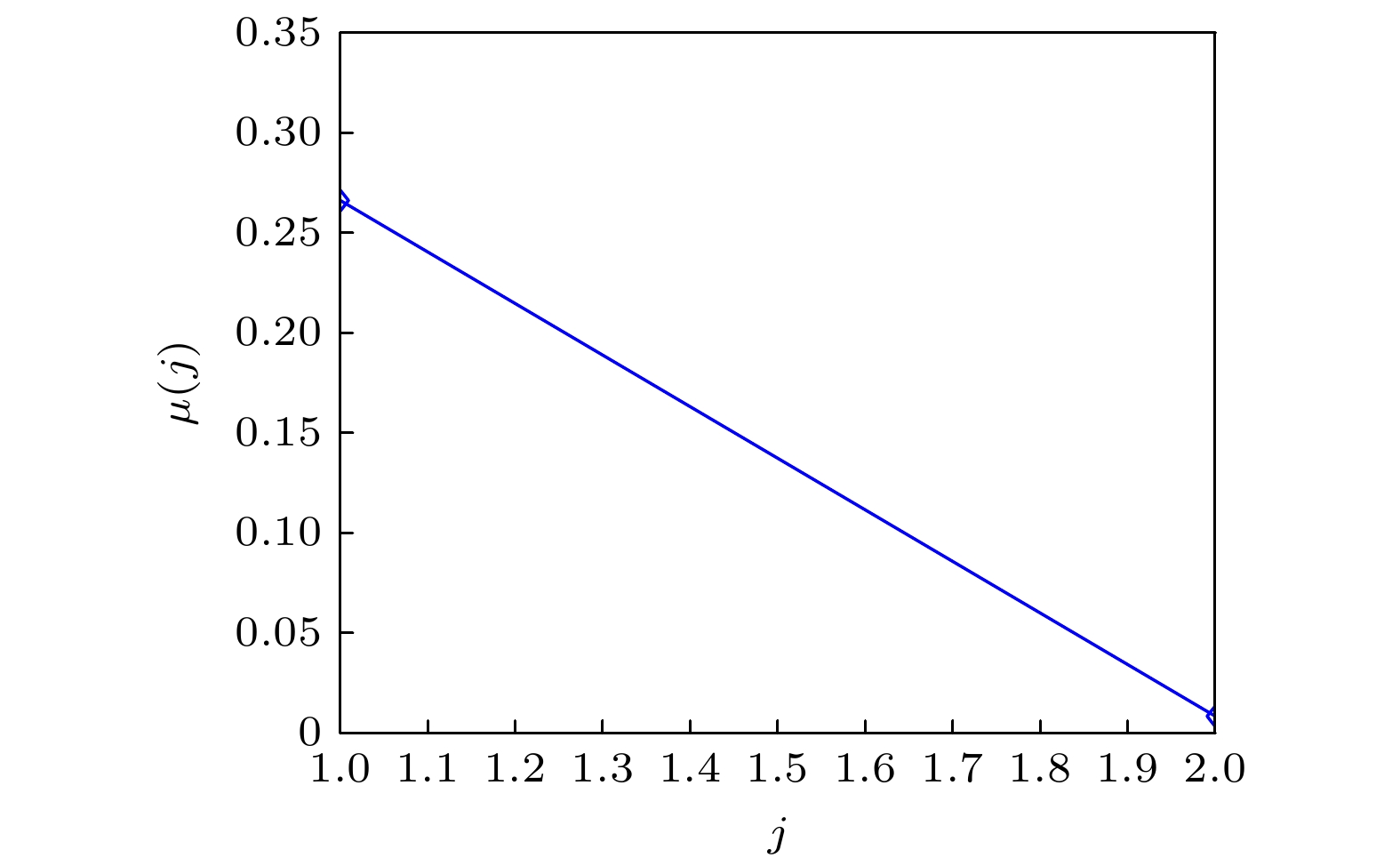
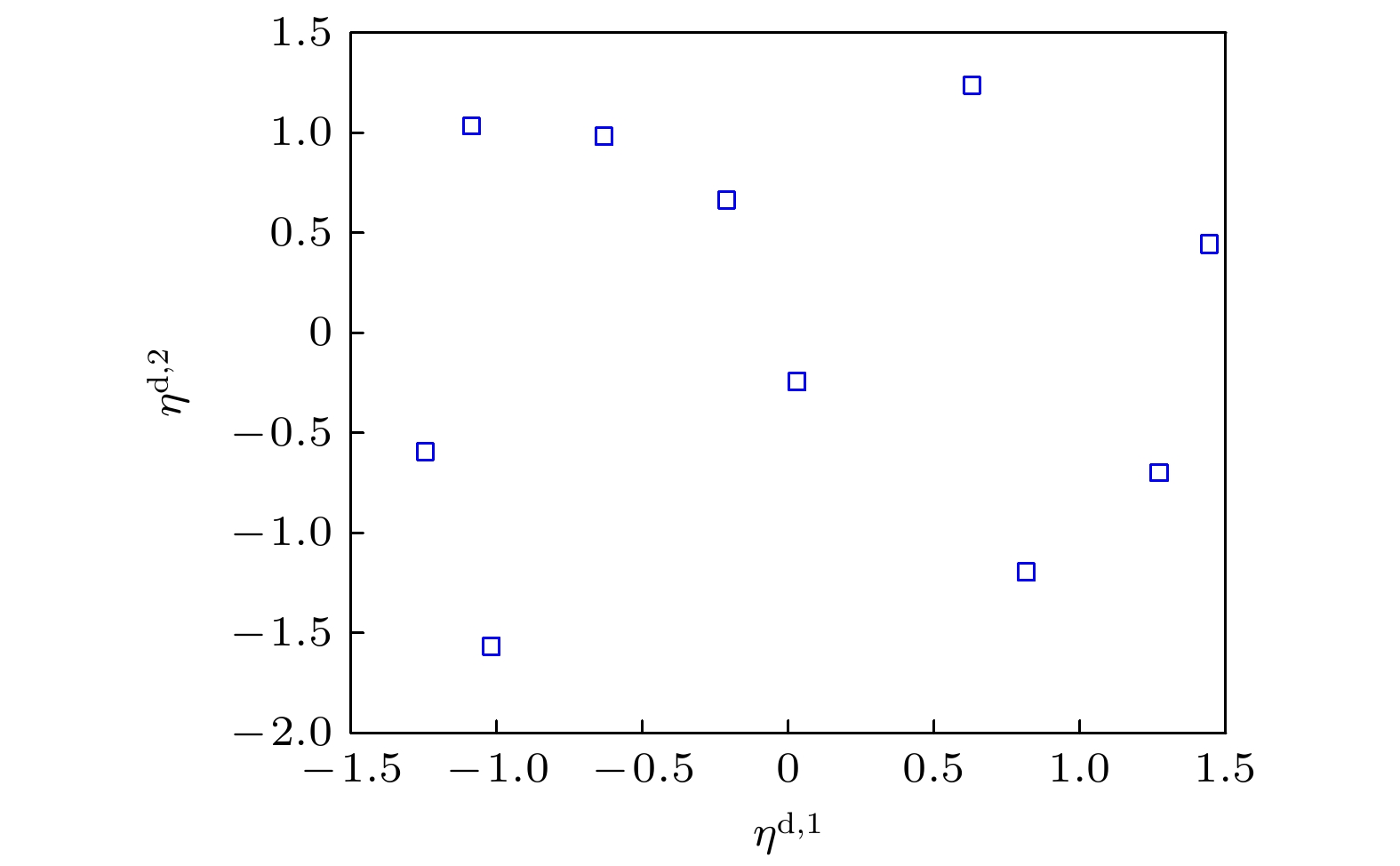
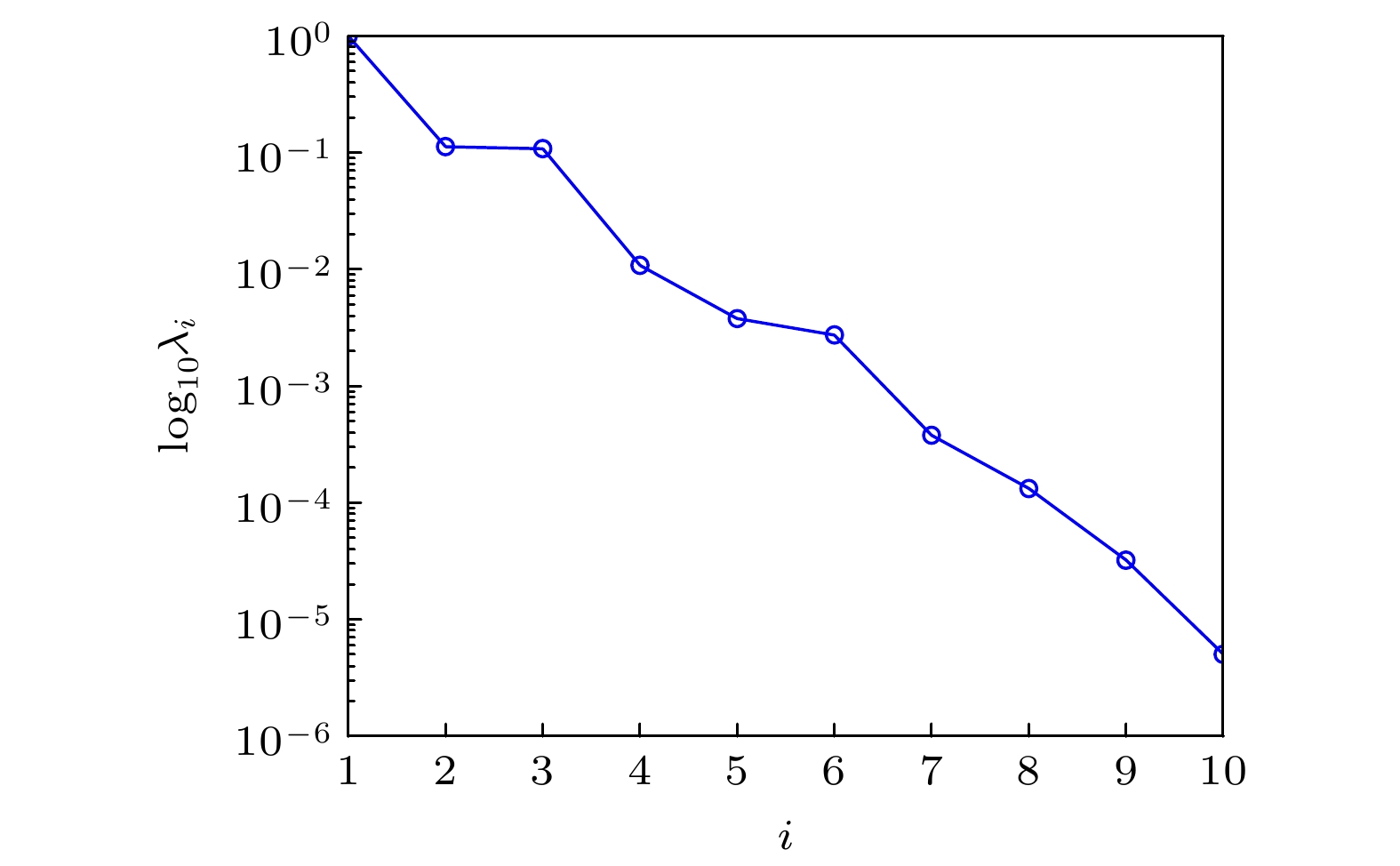
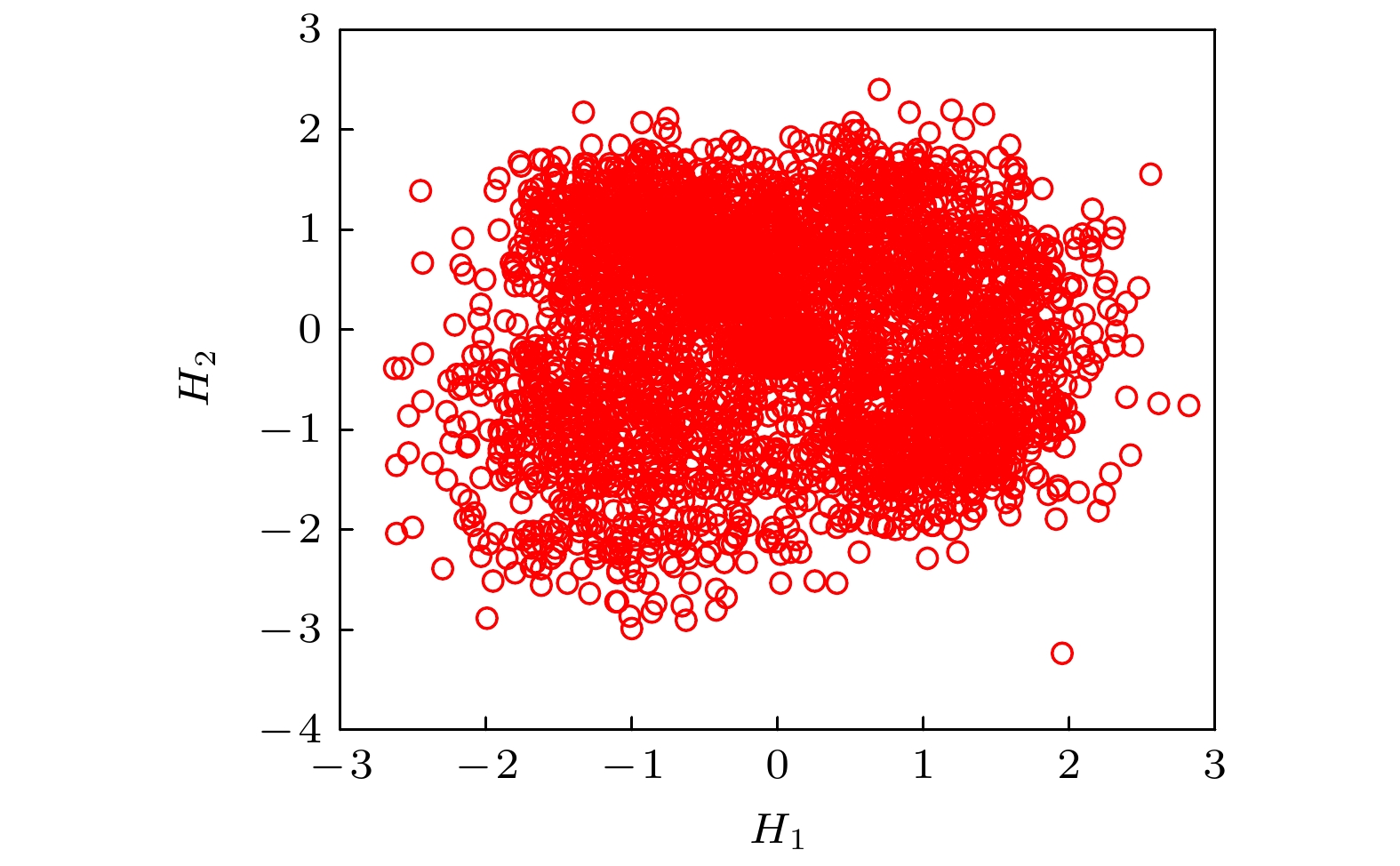
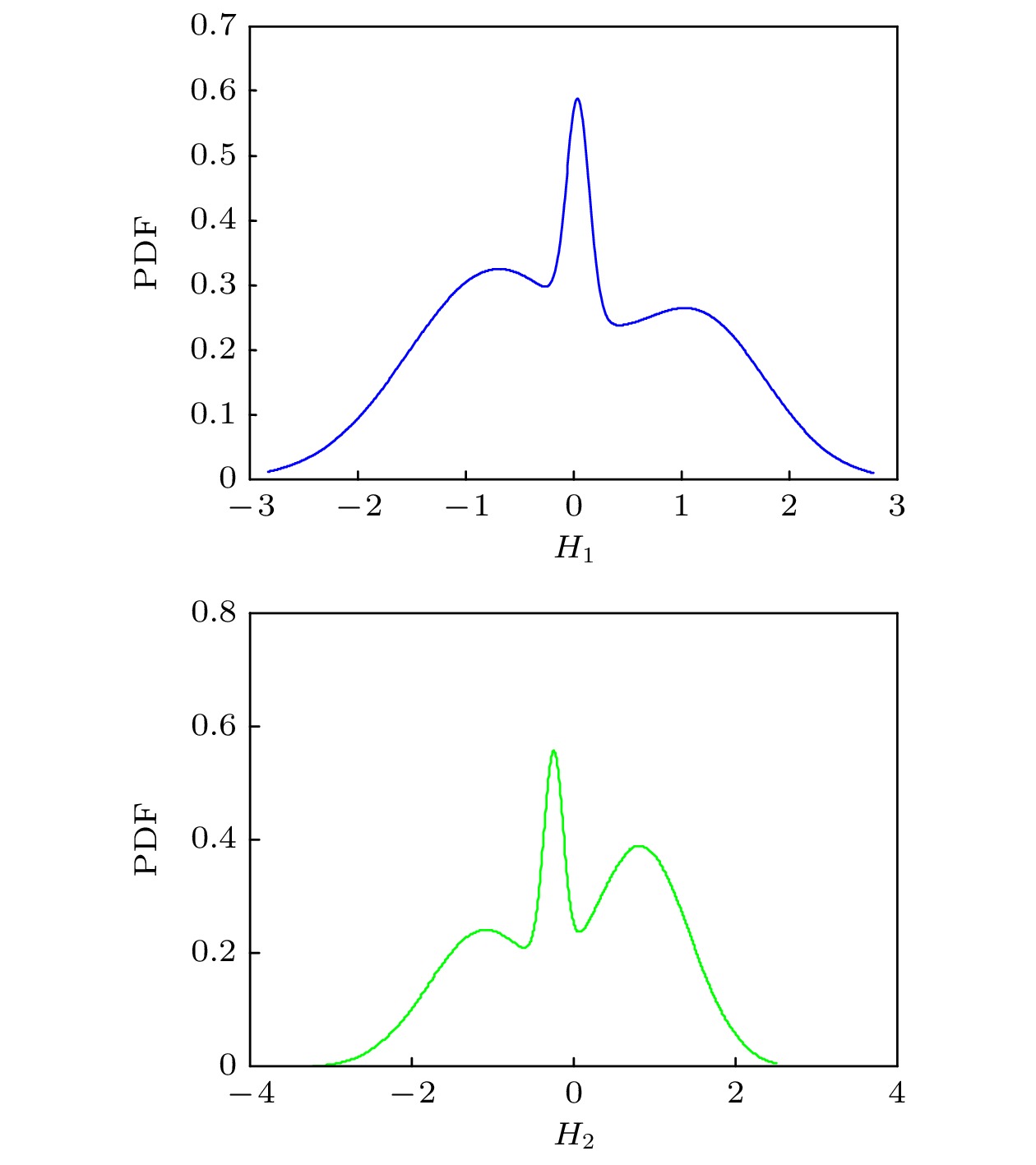
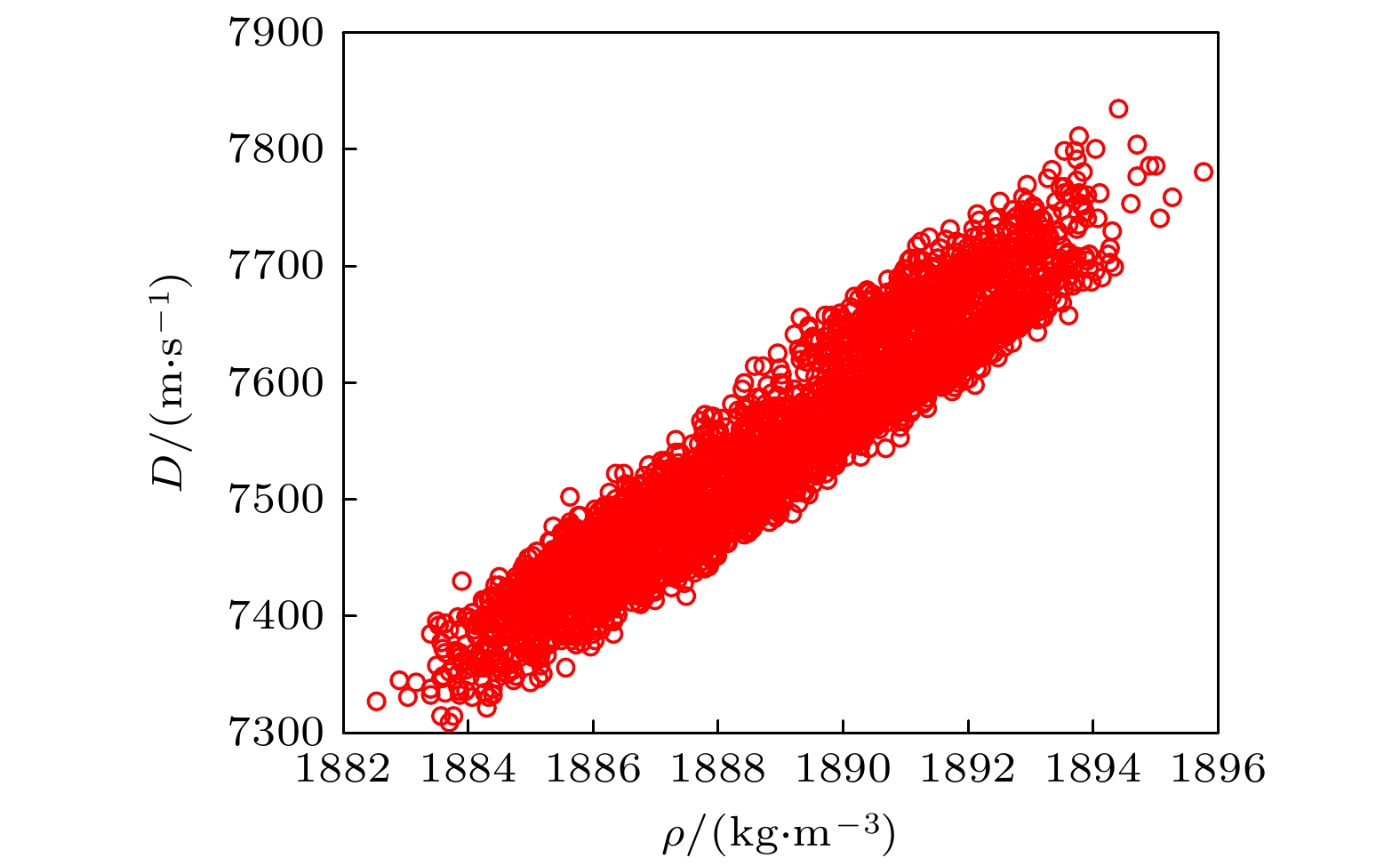
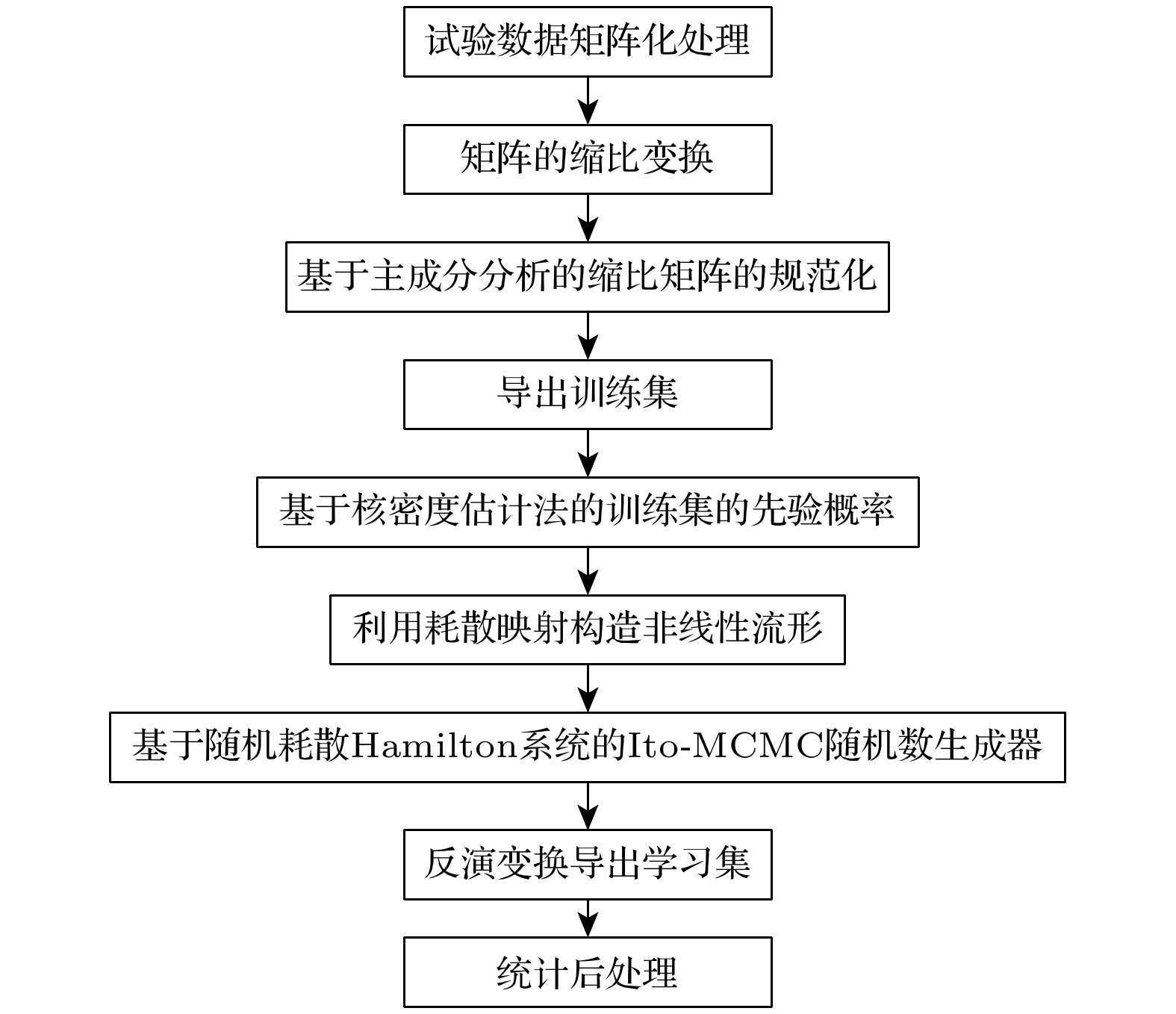
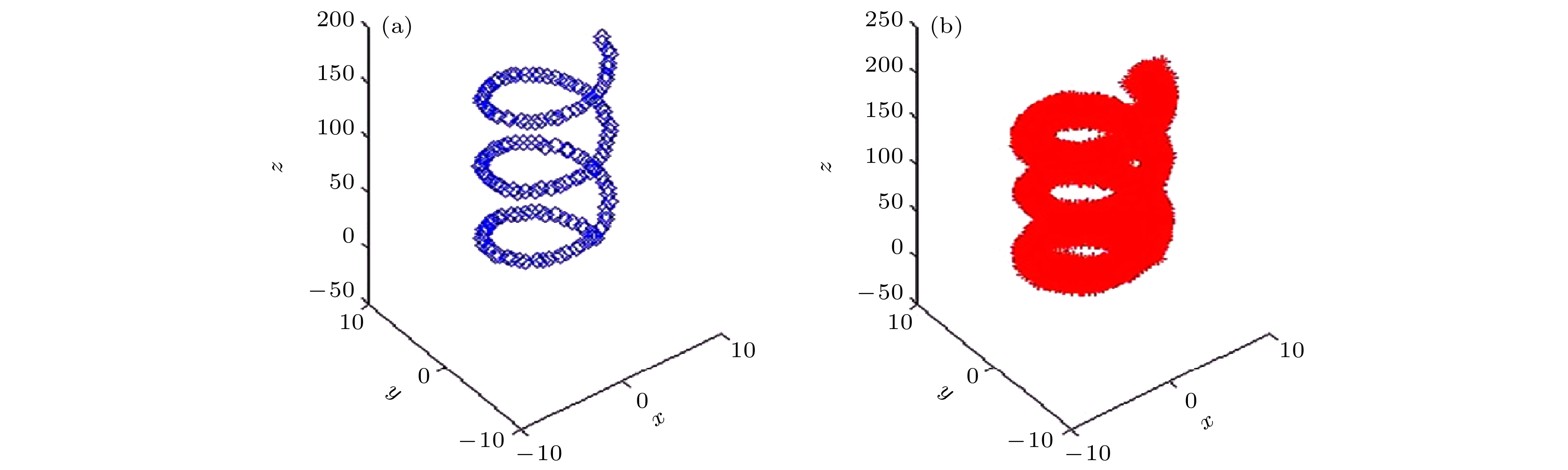
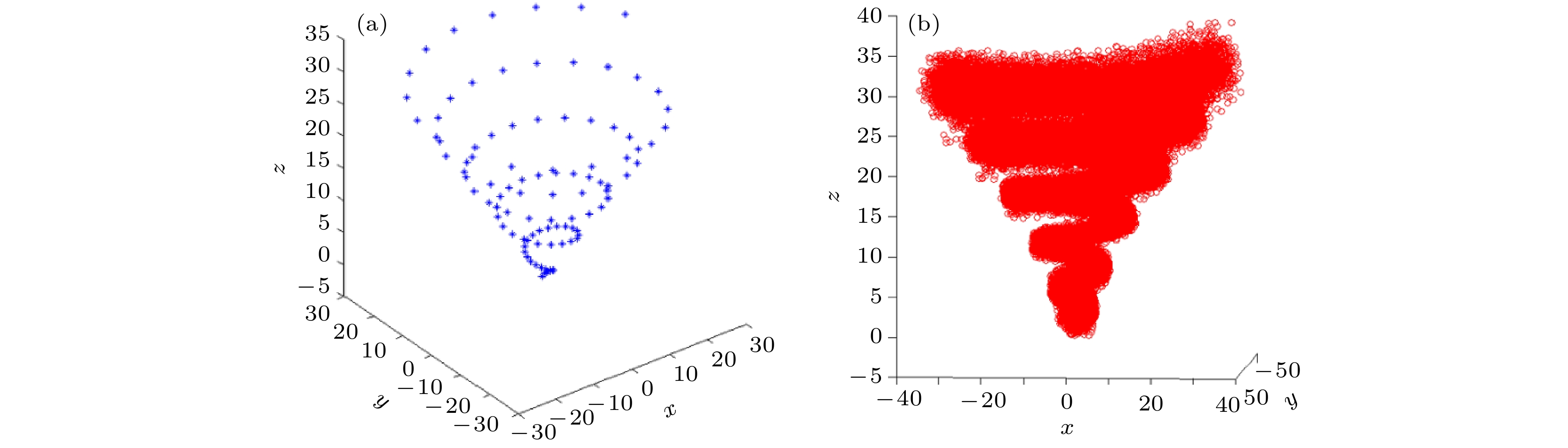
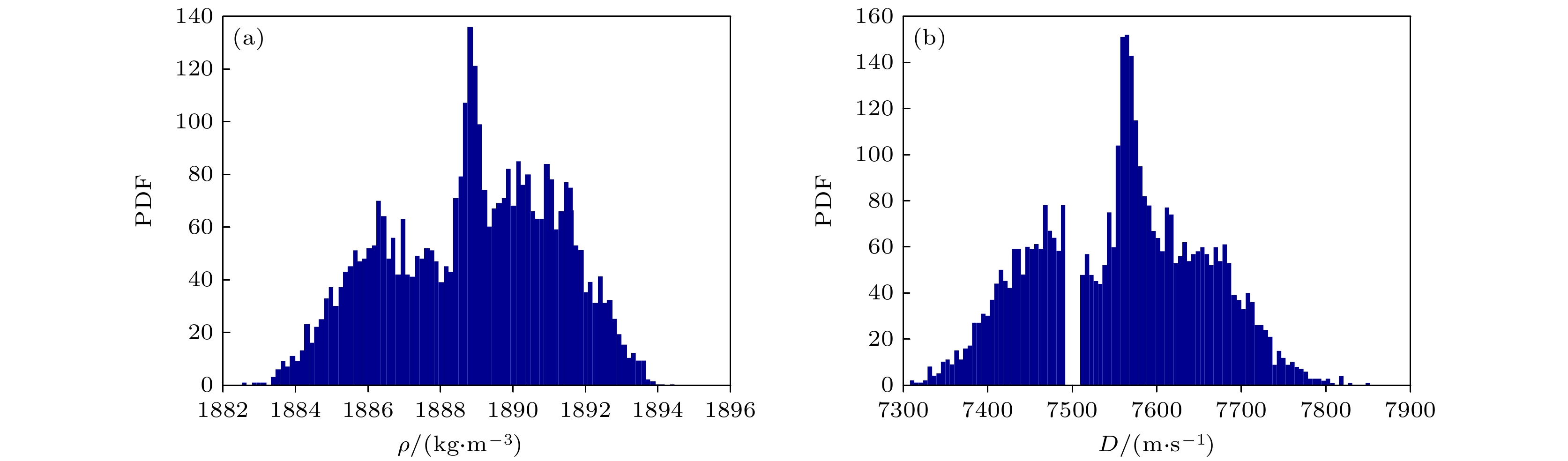
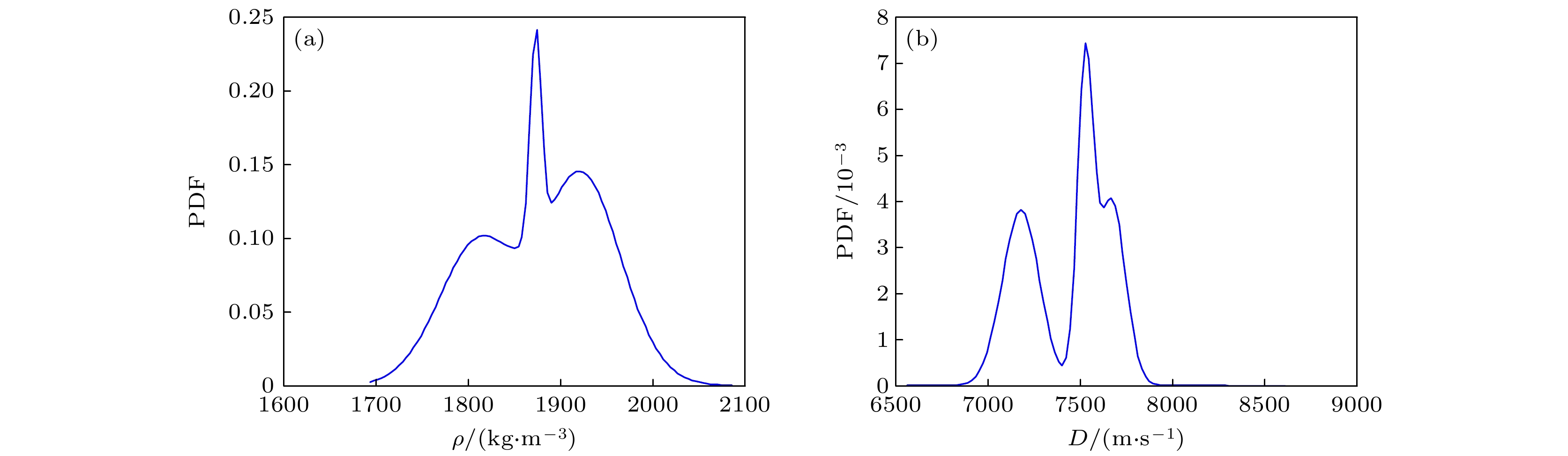
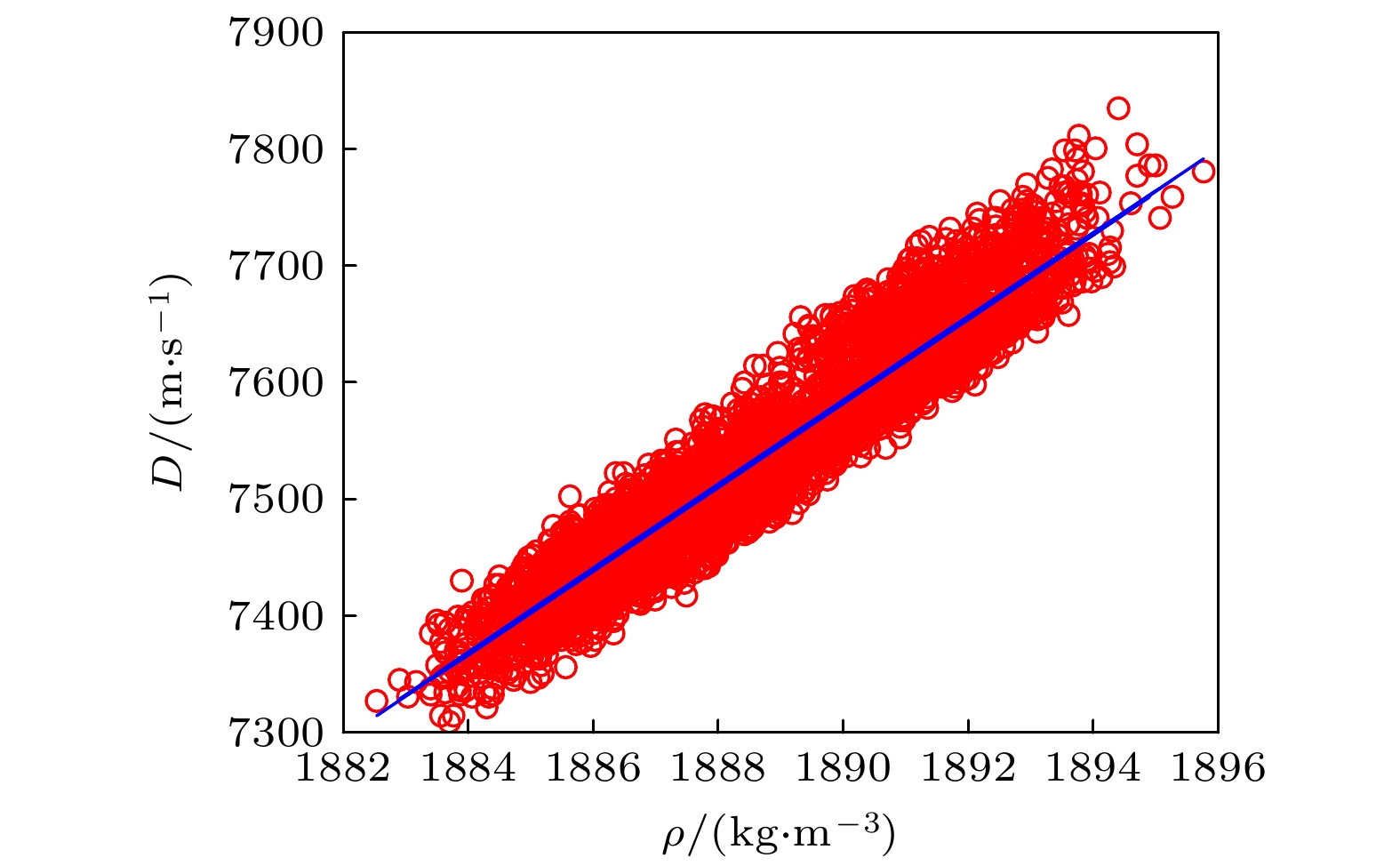
Detonation test is affected by small experimental datasets due to high risk of implementation and the huge cost of sample production and measurement. The major challenges of limited data consist in constructing the probability distribution of physical quantities and application of machine learning. Probability learning on manifold (PLoM) can generate a large number of implementations that are consistent with practical common knowledge, while preserving potential physical mechanism these generated samples. So PLoM is viewed as an efficient tool of tackling small samples. To begin with, experimental data are assumed to be concentrated on an unknown subset of Euclidean space and can be treated as the sampling of random vector to be determined. Meanwhile, experimental problem is solved in the framework of matrix and the scaling transformation is conducted on the datasets of PBX9502 with multi-physics attributes. Then the principal component analysis is utilized to normalize the scaling matrix, and the normalization matrix is labeled as training sets. Moreover, the altered multi-dimensional Gaussian kernel density estimation is utilized for estimating the probability distribution of training set. Furthermore, diffusion map is used to discover and characterize the geometry and structure of dataset. In other words, nonlinear manifold based on the training set is constructed through diffusion map. Specifically, the first eigenvalue and corresponding eigenvector is related to the construction of diffusion basis and diffusion maps. Further, Itô-MCMC sampler is associated with dissipative Hamilton system driven by Wiener process, for which the initial condition is set to be training set, and prior probability is conceived as invariant measure. Störmer-Verlet scheme is used for solving the stochastic dissipative Hamilton equations. Finally, additional realizations of learning dataset are fulfilled through the inversion transformation. The result shows that random number generated from PLoM satisfies the requirements of industrial and high fidelity simulation. The 95% confidence interval of density is included in the range calibrated by Los Alamos National Laboratory. And the value of detonation velocity calibrated by Prof. Chengwei Sun [Sun C W, Wei Y Z, Zhou Z K 2000 Applied Detonation Physics (Beijing: National Defense Industry Press) p224] also falls into 95% confidence interval of detonation velocity generated by PLoM. It is also deduced from the learning set that density and detonation velocity satisfies the affine transformation. Furthermore, detonation pressure has nonlinear relationship with density. Tiny variation of density can lead to magnificent fluctuation of detonation pressure and detonation velocity. Detonation pressure has the largest discreetness in all the physical quantities through the comparison of variation coefficients of learning set, which coincides with the existing research results. The method used is universal enough and can be extended to other detonation systems.
-
Keywords:
- probabilistic learning on manifold /
- diffusion map /
- stochastic dissipative Hamilton equations /
- small datasets /
- detonation /
- uncertainty quantification
[1] 孙承纬, 卫玉章, 周之奎 2000 应用爆轰物理 (北京: 国防工业出版社)
Sun C W, Wei Y Z, Zhou Z K 2000 Applied Detonation Physics (Beijing: National Defense Industry Press
[2] Mader C 1979 Numerical Modeling of Detonations (Berkeley: University of California
[3] 梁霄, 王瑞利, 胡星志, 陈江涛 2023 爆炸与冲击 43 71
 Google Scholar
Google Scholar
Liang X, Wang R L, Hu Z X, Chen J T 2023 Explos. Shock. Waves. 43 71
 Google Scholar
Google Scholar
[4] 梁霄, 王瑞利 2024 兵工学报 45 1673
 Google Scholar
Google Scholar
Liang X, Wang R L 2024 Acta. Arma. 45 1673
 Google Scholar
Google Scholar
[5] Liang X, Wang R L 2020 Int. J. Uncertainty. Quantif. 10 83
 Google Scholar
Google Scholar
[6] Bratton R N, Avramova M, Ivanov K 2014 Nucl. Eng. Technol. 46 313
 Google Scholar
Google Scholar
[7] Cartwright K, Pointon T, Oliver B V, Swanekamp S B, Hinshelwood D, Angus J R, Richardson A S, Mosher D 2016 Direct Electron-beam-injection Experiments for Validation of Air-chemistry Models (New Mexico: Sandia National Laboratories) SAND2016-2437C
[8] Los Alamos National Laboratory 2022 Advanced Simulation and Computing Simulation Strategy Report LA-UR-22-25074
[9] 胡泽华, 叶涛, 刘雄国, 王佳 2017 66 012801
 Google Scholar
Google Scholar
Hu Z H, Ye T, Liu X G, Wang J 2017 Acta. Phys. Sin. 66 012801
 Google Scholar
Google Scholar
[10] AIAA 1998 Guide for the Verification and Validation of Computational Fluid Dynamics Simulations (AIAA G-077-1998
[11] Clark M A, Kearns K, Overholt J L, Gross K H, Barthelemy B, Reed C 2014 Air Force Research Laboratory Test and Evaluation, Verification and Validation of Autonomous Systems Challenge Exploration Final Report Case Number 88ABW-2014-4063
[12] Hu X Z, Duan Y H, Wang R L, Liang X, Chen J T 2019 J. Verif. Valid. Uncert. 4 021006
 Google Scholar
Google Scholar
[13] 张诗琪, 杨化通 2023 72 110303
 Google Scholar
Google Scholar
Zhang S Q, Yang H T 2023 Acta. Phys. Sin. 72 110303
 Google Scholar
Google Scholar
[14] Wishart J, Como S, Forgione U, Weast J, Weston L, Smart A, Nicols G, Ramesh S 2020 SAE Int. J. CAV 3 267
 Google Scholar
Google Scholar
[15] Department of Energy’s NNSA 2005 Holistic, Hierarchical VVUQ as the Scientific Method for PSAAP Report LA-UR-23-32192
[16] Department of Defense 2019 Modeling and Simulation (M&S) Verification, Validation, and Accreditation (VV&A) Recommended Practices Guide (RPG) Core Document: Introduction
[17] Dahm W 2010 Technology Horizons a Vision for Air Force Science & Technology During 2010-2030 Report AF/ST-TR-10-01-PR
[18] Balci O 1994 Ann. Oper. Res. 53 121
 Google Scholar
Google Scholar
[19] Metzger E J, Barton N P, Smedstad O M, Ruston B C, Wallcraft A J, Whitcomb T R, Ridout J A, Franklin D S, Zamudio L, Posey P G, Reynolds C A, Phelps M 2016 Verification and Validation of a Navy ESPC Hindcast with Loosely Coupled data Assimilation American Geophysical Union A41G-0130
[20] American Society of Mechanical Engineers 2022 Verification, Validation, and Uncertainty Quantification Terminology in Computational Modeling and Simulation ASME VVUQ 1-2022
[21] Oberkampf W, Roy C 2010 Verification and Validation in Scientific Computing (Cambridge: Cambridge University Press
[22] Liang X, Wang R L 2019 Def. Technol. 15 398
 Google Scholar
Google Scholar
[23] 王言金, 张树道, 李华, 周海兵 2016 65 106401
 Google Scholar
Google Scholar
Wang Y J, Zhang S D, Li H, Zhou H B 2016 Acta. Phys. Sin. 65 106401
 Google Scholar
Google Scholar
[24] Park C, Nili S, Mathew J T, Ouellet F, Koneru R, Kim N, Balachandar S, Haftka R 2021 J. Verif. Valid. Uncert. 6 119007
 Google Scholar
Google Scholar
[25] 梁霄, 王瑞利 2017 66 116401
 Google Scholar
Google Scholar
Liang X, Wang R L 2017 Acta. Phys. Sin. 66 116401
 Google Scholar
Google Scholar
[26] Soize C, Ghanem R 2016 J. Comput. Phys. 321 242
 Google Scholar
Google Scholar
[27] Ghanem R, Soize C, Safta C, Huan X, Lacaze G, Oefelein J C, Najm H N 2019 J. Comput. Phys. 399 108930
 Google Scholar
Google Scholar
[28] Capiez-Lernout E, Ezvan O, Soize C 2024 J. Comput. Inf. Sci. Eng. 24 061006
 Google Scholar
Google Scholar
[29] Nespoulous J, Perrin G, Funfschilling C, Soize C 2024 Physics D 457 133977
 Google Scholar
Google Scholar
[30] Capiez-Lernout E, Soize C 2022 Int. J. Non. Linear. Mech. 143 104023
 Google Scholar
Google Scholar
[31] Metropolis N, Ulam S 1949 J. Am. Stat. Assoc. 44 335
 Google Scholar
Google Scholar
[32] Hastings W 1970 Biometrika 109 57
 Google Scholar
Google Scholar
[33] Geman S, Geman D 1984 IEEE Trans. Pattern. Anal. Mach. Intell. 6 721
 Google Scholar
Google Scholar
[34] Campbell A 1984 Pyrotechnics 9 183
 Google Scholar
Google Scholar
[35] Peterson P, Idar D 2005 Propell. Explos. Pyrot. 30 88
 Google Scholar
Google Scholar
[36] Davis W C, Hill L G 2002 12th International Symposium Detonation San Diego, USA, August 11–16, 2002 p220
[37] Handley C, Lambourn B, Whitworth N, James H, Belfield W 2018 Appl. Phys. Rev. 5 011303
 Google Scholar
Google Scholar
[38] Coifman R, Lafon S, Lee A, Maggioni M, Nadler B, Warner F 2005 Proc. Natl. Acad. Sci. USA 102 7426
 Google Scholar
Google Scholar
[39] Hairer E, Lubich C, Wanner G 2002 Geometric Numerical Integration Structure-Preserving Algorithms for Ordinary Differential Equations (Heidelberg: Springer-Verlag
[40] Soize C 2008 Int. J. Numer. Methods Eng. 76 1583
 Google Scholar
Google Scholar
[41] Shannon C 1948 Bell. Syst. Tech. J. 27 623
 Google Scholar
Google Scholar
[42] Gustavsen R, Sheffield S, Alcon R 2006 J. Appl. Phys. 99 114907
 Google Scholar
Google Scholar
-
-
[1] 孙承纬, 卫玉章, 周之奎 2000 应用爆轰物理 (北京: 国防工业出版社)
Sun C W, Wei Y Z, Zhou Z K 2000 Applied Detonation Physics (Beijing: National Defense Industry Press
[2] Mader C 1979 Numerical Modeling of Detonations (Berkeley: University of California
[3] 梁霄, 王瑞利, 胡星志, 陈江涛 2023 爆炸与冲击 43 71
 Google Scholar
Google Scholar
Liang X, Wang R L, Hu Z X, Chen J T 2023 Explos. Shock. Waves. 43 71
 Google Scholar
Google Scholar
[4] 梁霄, 王瑞利 2024 兵工学报 45 1673
 Google Scholar
Google Scholar
Liang X, Wang R L 2024 Acta. Arma. 45 1673
 Google Scholar
Google Scholar
[5] Liang X, Wang R L 2020 Int. J. Uncertainty. Quantif. 10 83
 Google Scholar
Google Scholar
[6] Bratton R N, Avramova M, Ivanov K 2014 Nucl. Eng. Technol. 46 313
 Google Scholar
Google Scholar
[7] Cartwright K, Pointon T, Oliver B V, Swanekamp S B, Hinshelwood D, Angus J R, Richardson A S, Mosher D 2016 Direct Electron-beam-injection Experiments for Validation of Air-chemistry Models (New Mexico: Sandia National Laboratories) SAND2016-2437C
[8] Los Alamos National Laboratory 2022 Advanced Simulation and Computing Simulation Strategy Report LA-UR-22-25074
[9] 胡泽华, 叶涛, 刘雄国, 王佳 2017 66 012801
 Google Scholar
Google Scholar
Hu Z H, Ye T, Liu X G, Wang J 2017 Acta. Phys. Sin. 66 012801
 Google Scholar
Google Scholar
[10] AIAA 1998 Guide for the Verification and Validation of Computational Fluid Dynamics Simulations (AIAA G-077-1998
[11] Clark M A, Kearns K, Overholt J L, Gross K H, Barthelemy B, Reed C 2014 Air Force Research Laboratory Test and Evaluation, Verification and Validation of Autonomous Systems Challenge Exploration Final Report Case Number 88ABW-2014-4063
[12] Hu X Z, Duan Y H, Wang R L, Liang X, Chen J T 2019 J. Verif. Valid. Uncert. 4 021006
 Google Scholar
Google Scholar
[13] 张诗琪, 杨化通 2023 72 110303
 Google Scholar
Google Scholar
Zhang S Q, Yang H T 2023 Acta. Phys. Sin. 72 110303
 Google Scholar
Google Scholar
[14] Wishart J, Como S, Forgione U, Weast J, Weston L, Smart A, Nicols G, Ramesh S 2020 SAE Int. J. CAV 3 267
 Google Scholar
Google Scholar
[15] Department of Energy’s NNSA 2005 Holistic, Hierarchical VVUQ as the Scientific Method for PSAAP Report LA-UR-23-32192
[16] Department of Defense 2019 Modeling and Simulation (M&S) Verification, Validation, and Accreditation (VV&A) Recommended Practices Guide (RPG) Core Document: Introduction
[17] Dahm W 2010 Technology Horizons a Vision for Air Force Science & Technology During 2010-2030 Report AF/ST-TR-10-01-PR
[18] Balci O 1994 Ann. Oper. Res. 53 121
 Google Scholar
Google Scholar
[19] Metzger E J, Barton N P, Smedstad O M, Ruston B C, Wallcraft A J, Whitcomb T R, Ridout J A, Franklin D S, Zamudio L, Posey P G, Reynolds C A, Phelps M 2016 Verification and Validation of a Navy ESPC Hindcast with Loosely Coupled data Assimilation American Geophysical Union A41G-0130
[20] American Society of Mechanical Engineers 2022 Verification, Validation, and Uncertainty Quantification Terminology in Computational Modeling and Simulation ASME VVUQ 1-2022
[21] Oberkampf W, Roy C 2010 Verification and Validation in Scientific Computing (Cambridge: Cambridge University Press
[22] Liang X, Wang R L 2019 Def. Technol. 15 398
 Google Scholar
Google Scholar
[23] 王言金, 张树道, 李华, 周海兵 2016 65 106401
 Google Scholar
Google Scholar
Wang Y J, Zhang S D, Li H, Zhou H B 2016 Acta. Phys. Sin. 65 106401
 Google Scholar
Google Scholar
[24] Park C, Nili S, Mathew J T, Ouellet F, Koneru R, Kim N, Balachandar S, Haftka R 2021 J. Verif. Valid. Uncert. 6 119007
 Google Scholar
Google Scholar
[25] 梁霄, 王瑞利 2017 66 116401
 Google Scholar
Google Scholar
Liang X, Wang R L 2017 Acta. Phys. Sin. 66 116401
 Google Scholar
Google Scholar
[26] Soize C, Ghanem R 2016 J. Comput. Phys. 321 242
 Google Scholar
Google Scholar
[27] Ghanem R, Soize C, Safta C, Huan X, Lacaze G, Oefelein J C, Najm H N 2019 J. Comput. Phys. 399 108930
 Google Scholar
Google Scholar
[28] Capiez-Lernout E, Ezvan O, Soize C 2024 J. Comput. Inf. Sci. Eng. 24 061006
 Google Scholar
Google Scholar
[29] Nespoulous J, Perrin G, Funfschilling C, Soize C 2024 Physics D 457 133977
 Google Scholar
Google Scholar
[30] Capiez-Lernout E, Soize C 2022 Int. J. Non. Linear. Mech. 143 104023
 Google Scholar
Google Scholar
[31] Metropolis N, Ulam S 1949 J. Am. Stat. Assoc. 44 335
 Google Scholar
Google Scholar
[32] Hastings W 1970 Biometrika 109 57
 Google Scholar
Google Scholar
[33] Geman S, Geman D 1984 IEEE Trans. Pattern. Anal. Mach. Intell. 6 721
 Google Scholar
Google Scholar
[34] Campbell A 1984 Pyrotechnics 9 183
 Google Scholar
Google Scholar
[35] Peterson P, Idar D 2005 Propell. Explos. Pyrot. 30 88
 Google Scholar
Google Scholar
[36] Davis W C, Hill L G 2002 12th International Symposium Detonation San Diego, USA, August 11–16, 2002 p220
[37] Handley C, Lambourn B, Whitworth N, James H, Belfield W 2018 Appl. Phys. Rev. 5 011303
 Google Scholar
Google Scholar
[38] Coifman R, Lafon S, Lee A, Maggioni M, Nadler B, Warner F 2005 Proc. Natl. Acad. Sci. USA 102 7426
 Google Scholar
Google Scholar
[39] Hairer E, Lubich C, Wanner G 2002 Geometric Numerical Integration Structure-Preserving Algorithms for Ordinary Differential Equations (Heidelberg: Springer-Verlag
[40] Soize C 2008 Int. J. Numer. Methods Eng. 76 1583
 Google Scholar
Google Scholar
[41] Shannon C 1948 Bell. Syst. Tech. J. 27 623
 Google Scholar
Google Scholar
[42] Gustavsen R, Sheffield S, Alcon R 2006 J. Appl. Phys. 99 114907
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 520
- PDF Downloads: 16
- Cited By: 0














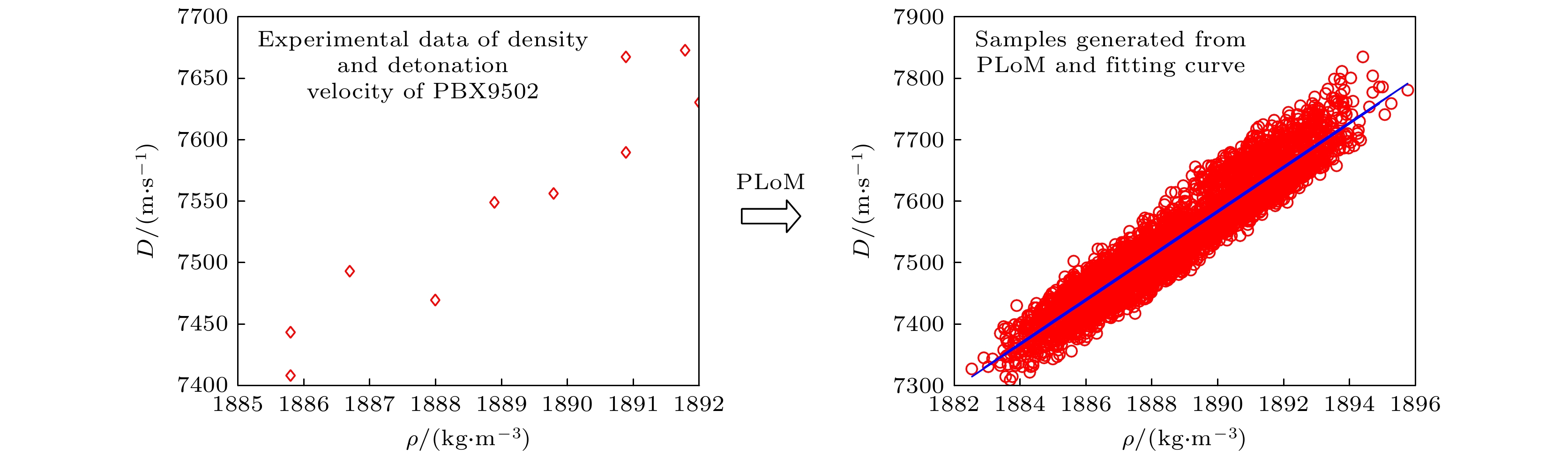
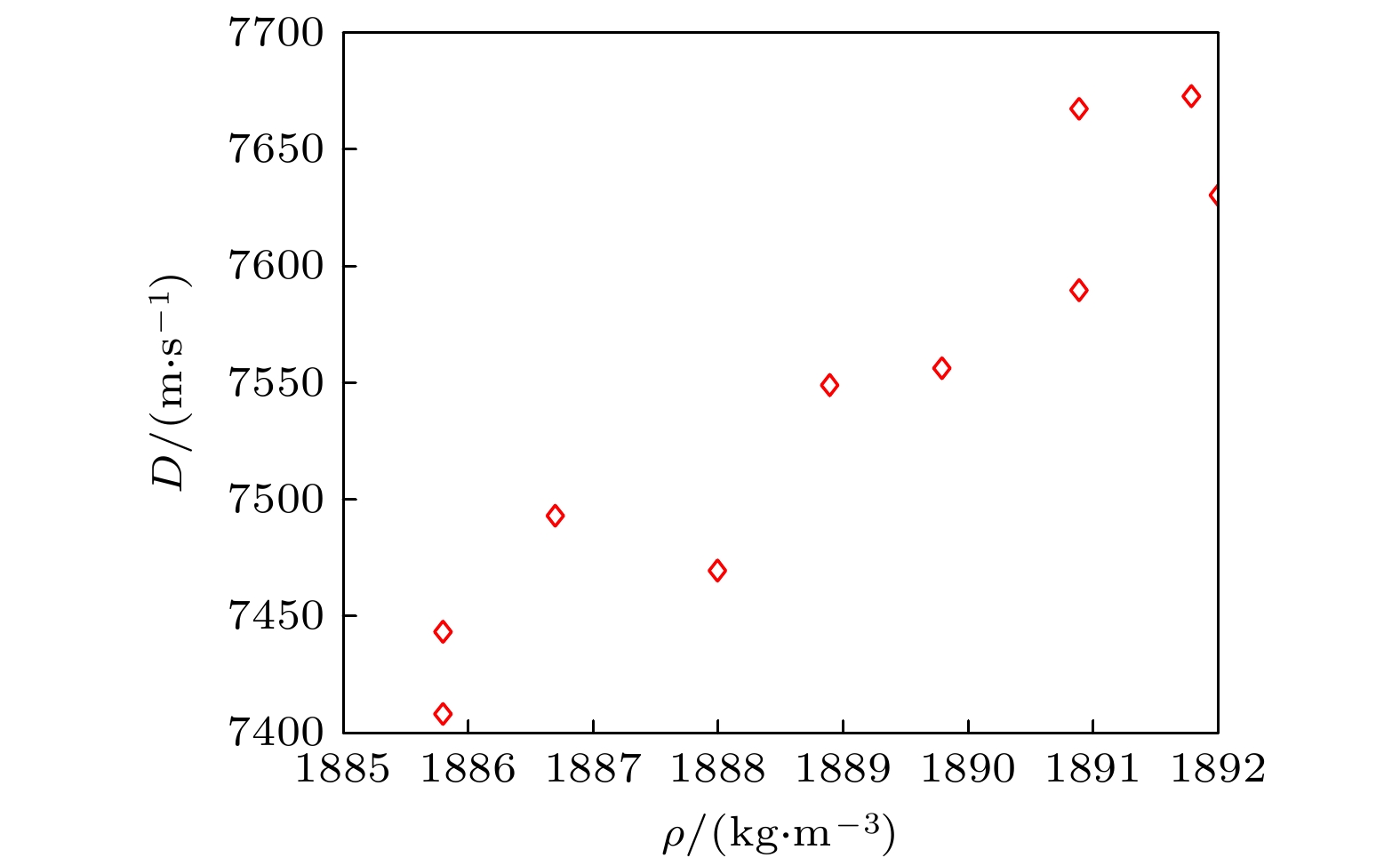
 DownLoad:
DownLoad: