Implementation and simulation of direct Doppler wind measurement technology under regime of multi-longitudinal mode laser

Gao Feng-Jia; Gao Fei; Zhao Ting-Ting; Wang Li; Li Shi-Chun; Yan Qing; Hua Deng-Xin

doi:10.7498/aps.73.20240949

Abstract

Single-longitudinal-mode (SLM) direct Doppler wind lidar (DDWL) requires complex techniques of the seed injection, high precision frequency stability, and frequency locking to provide an output of the stable frequency SLM laser, resulting in a complex structure of DDWL. To reduce the technical difficulty and structural complexity of the excitation light source of DDWL, a multi-longitudinal mode (MLM) DDWL is proposed. In the MLM DDWL, a free-running MLM laser is directly used as an excitation light source and quadri-channel Mach-Zender interferometer (QMZI) with four periodic outputs is adopted as a spectral discriminator.Firstly, for the typical Nd:YAG pulsed laser, the scattering spectra of atmospheric elastic echo excited by the MLM laser are analyzed which are coincident with the longitudinal modes of the MLM laser. The peaks of atmospheric elastic echo scattering spectra excited by the MLM laser overlap with each other. The overlapping degree is affected by the laser radiation linewidth, laser optical resonator length, laser center wavelength, and type of scattering particles. In addition, the scattering spectra of atmospheric elastic echo excited by each longitudinal mode of the MLM laser have the Doppler frequency shift introduced by atmospheric wind. Therefore, it is necessary to select an optical interferometer with the periodic transmittance curve as the spectral discriminator of MLM DDWL.Subsequently, a QMZI is designed as the spectral discriminator to achieve high-precision measurement for the Doppler frequency shift of scattering spectra of atmospheric elastic echo excited by the MLM laser. The designed QMZI has four periodic output channels and the phase difference between adjacent channels is π/2. The mathematical model of the transmittance function of the QMZI is established. The effective transmittance of the QMZI for atmospheric elastic echo scattering spectrum excited by the MLM laser is analyzed based on the partial coherence theory of quasi-monochromatic light interference and the polarization effect of light. On this basis, the data inversion algorithm of MLM DDWL is constructed.Finally, the simulation experiments of wind measurement are carried out. The QMZI simulation model is built by the non-sequential mode of Zemax optical simulation software. The atmospheric elastic echo scattering spectra excited by the MLM laser are configured by the SPCD files of Zemax optical simulation software under different theoretical wind speeds ranging from –50 to 50 m/s, laser optical resonator lengths (L = 30 mm and 300 mm), and laser center wavelengths (λ = 1064, 532, and 355 nm). The SPCD files are fed to the QMZI simulation model as input signals. At the same time, the ray tracing on input signal is performed based on the principle of Monte Carlo simulation s, and the output signals of the four channels of the QMZI simulation model are recorded to retrieve the atmospheric wind information. The simulation results show that the proposed MLM DDWL can achieve high-precision measurement of atmospheric wind information. With the laser optical resonator length of 300 mm and laser center wavelengths λ = 1064 nm, λ = 532 nm, λ = 355 nm, the maximum detectable wind speeds of MLM DDWL are about 50, 30, and 20 m/s, and the wind measurement errors can be controlled within 2.5, 3.0, and 4.0 m/s, respectively. When the center wavelength of each laser is 532 nm, and the lengths of laser optical resonator are 30 mm and 300 mm, then the maximum detectable wind speeds of MLM DDWL are about 50 m/s and 30 m/s, and the wind measurement errors can be controlled within 2.0 m/s and 3.0 m/s, respectively. Therefore, the longer the laser center wavelength and the shorter the laser optical resonator length, the larger the wind measurement range will be and the smaller the wind measurement error.

Keywords:

Authors and contacts

1.
School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an 710048, China
2.
Shaanxi Collaborative Innovation Center for Modern Equipment Green Manufacturing, Xi’an 710048, China
3.
Key Laboratory of Metrological Optics and Application for State Market Regulation, Xi’an 710048, China

Corresponding author: Gao Fei, gaofei@xaut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 42175149, 41775035, 42275148), the China-CEEC Joint Higher Education Project (Grant Nos. 2023330, 2022232, 2021120), the Scientific Research Program Funded by Shaanxi Provincial Education Department, China (Grant No. 23JY055), the Open Project of Key Laboratory of Metrological Optics and Application for State Market Regulation, China (Grant No. SXJL2023Z01KF), and the Ph.D. Innovation Fund Project of Xi’an University of Technology, China (Grant No. 102-252072304).

FullText HTML : translate this paragraph

References

[1]	Kumar D, Premachandran B 2019 Int. J. Therm. Sci. 138 263 Google Scholar
[2]	Liu G Q, Perrie W 2013 Geophys. Res. Lett. 40 3150 Google Scholar
[3]	Gardiner B, Berry P, Moulia B 2016 Plant Sci. 245 94 Google Scholar
[4]	Yu L J, Zhong S Y, Bian X D, Heilman W E 2018 Int. J. Climatol. 39 1684
[5]	马福民, 陈涌, 杨泽后, 周鼎富, 李晓锋, 陈春利, 冯力天, 余臣 2019 激光与光电子学进展 56 180003 Google Scholar Ma F M, Chen Y, Yang Z H, Zhou D F, Li X F, Chen C L, Feng L T, Yu C 2019 Laser Optoelectron. Prog. 56 180003 Google Scholar
[6]	Reitebuch O, Lemmerz Ch, Nagel E, Paffrath U, Durand Y, Endemann M, Fabre F, Chaloupy M 2009 J. Atmos. Oceanic Technol. 26 2501 Google Scholar
[7]	Paffrath U, Lemmerz Ch, Reitebuch O, Oliver, Witschas B, Nikolaus I, Freudenthaler V 2009 J. Atmos. Oceanic Technol. 26 2516 Google Scholar
[8]	储玉飞, 刘东, 王珍珠, 吴德成, 邓迁, 李路, 庄鹏, 王英俭 2020 量子电子学报 37 580 Chu Y F, Liu D, Wang Z Z, Wu D C, Deng Q, Li L, Zhuang P, Wang Y J 2020 Chin. J. Quantum Electron. 37 580
[9]	Jiang S, Sun D S, Han Y L, Han F, Zhou A R, Zheng J 2019 Curr. Opt. Photonics 3 466
[10]	Zhang Y P, Yuan J L, Wu Y B, Dong J J, Xia H Y 2023 Phys. Rev. Fluids 8 L022701 Google Scholar
[11]	Zhang Y P, Wu Y B, Dong J J, Xia H Y 2022 IEEE Photonics J. 14 6047706
[12]	Liu Z L, Barlow J F, Chan P W, Fung J C H, Li Y G, Ren C, Mark H W L, Ng E 2019 Remote Sens. 11 2522 Google Scholar
[13]	张亚飞, 冯玉涛, 傅頔, 畅晨光, 李娟, 白清兰, 胡炳樑 2022 71 084201 Google Scholar Zhang Y F, Feng Y T, Fu D, Chang C G, Li J, Bai Q L, Hu B J 2022 Acta Phys. Sin. 71 084201 Google Scholar
[14]	Vrancken P, Herbst J 2022 Remote Sens. 14 3356 Google Scholar
[15]	Kliebisch O, Uittenbosch H, Thurn J, Mahnke P 2022 Opt. Express 30 5540 Google Scholar
[16]	Wang L, Gao F, Wang J, Yan Q, Yan W X, Wang M, Hua D X 2019 Opt. Laser Eng. 121 61 Google Scholar
[17]	Hill C 2018 Remote Sens. 10 466 Google Scholar
[18]	Shen F H, Wang B X, Shi W J, Zhuang P, Zhu C Y, Xie C B 2018 Opt. Commun. 412 7 Google Scholar
[19]	潘艺升, 闫召爱, 郭文杰, 徐轻尘, 胡雄 2016 激光技术 40 153 Pan Y S, Yan Z A, Guo W J, Xu Q C, Hu X 2016 Laser Technol. 40 153
[20]	Wu C T, Chen F, Dai T Y, Ju Y L 2015 J. Mod. Opt. 62 1535 Google Scholar
[21]	张明富, 杨天新, 葛春风 2022 红外与激光工程 51 20210435 Google Scholar Zhang M F, Yang T X, Ge C F 2022 Infrared Laser Eng. 51 20210435 Google Scholar
[22]	葛烨, 胡以华, 舒嵘, 洪光烈 2015 64 020707 Google Scholar Ge Y, Hu Y H, Shu R, Hong G L 2015 Acta Phys. Sin. 64 020707 Google Scholar
[23]	Bruneau D, Blouzon F, Spatazza J, Montmessin F, Pelon J, Faure B 2013 Appl. Opt. 52 4941 Google Scholar
[24]	高飞, 南恒帅, 黄波, 汪丽, 李仕春, 王玉峰, 刘晶晶, 闫庆, 宋跃辉, 华灯鑫 2018 67 030701 Google Scholar Gao F, Nan H S, Huang B, Wang L, Li S C, Wang Y F, Liu J J, Yan Q, Song Y H, Hua D X 2018 Acta Phys. Sin. 67 030701 Google Scholar
[25]	Gao F, Nan H S, Zhang R, Zhu Q S, Chen T, Wang L, Chen H, Hua D X, Stanic S 2019 J. Quant. Spectrosc. Radiat. Transfer 234 10 Google Scholar
[26]	毛艳丽, 邱宏伟, 徐军, 邓佩珍, 干福熹 2001 光学学报 21 1264 Mao Y L, Qiu H W, Xu J, Deng P Z, Gan F X 2001 Acta Opt. Sin. 21 1264
[27]	Korb C L, Gentry B M, Weng C Y 1992 Appl. Opt. 31 4202 Google Scholar
[28]	Thompson B J, Wolf E 1957 J. Opt. Soc. Am. 47 895 Google Scholar

Cited By

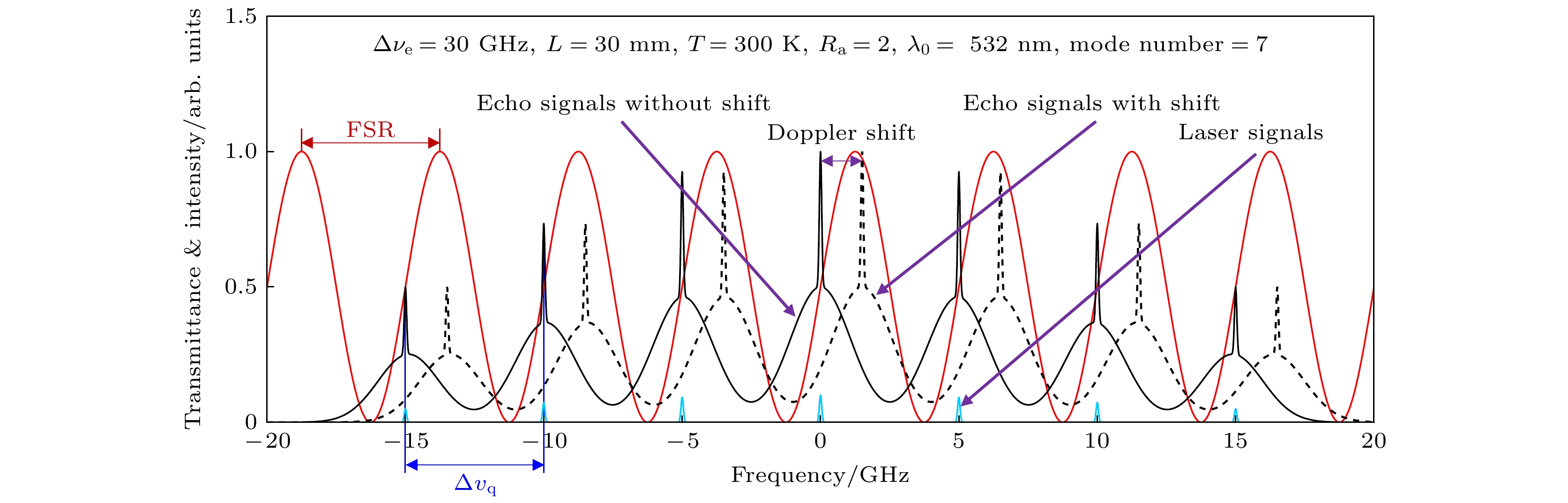
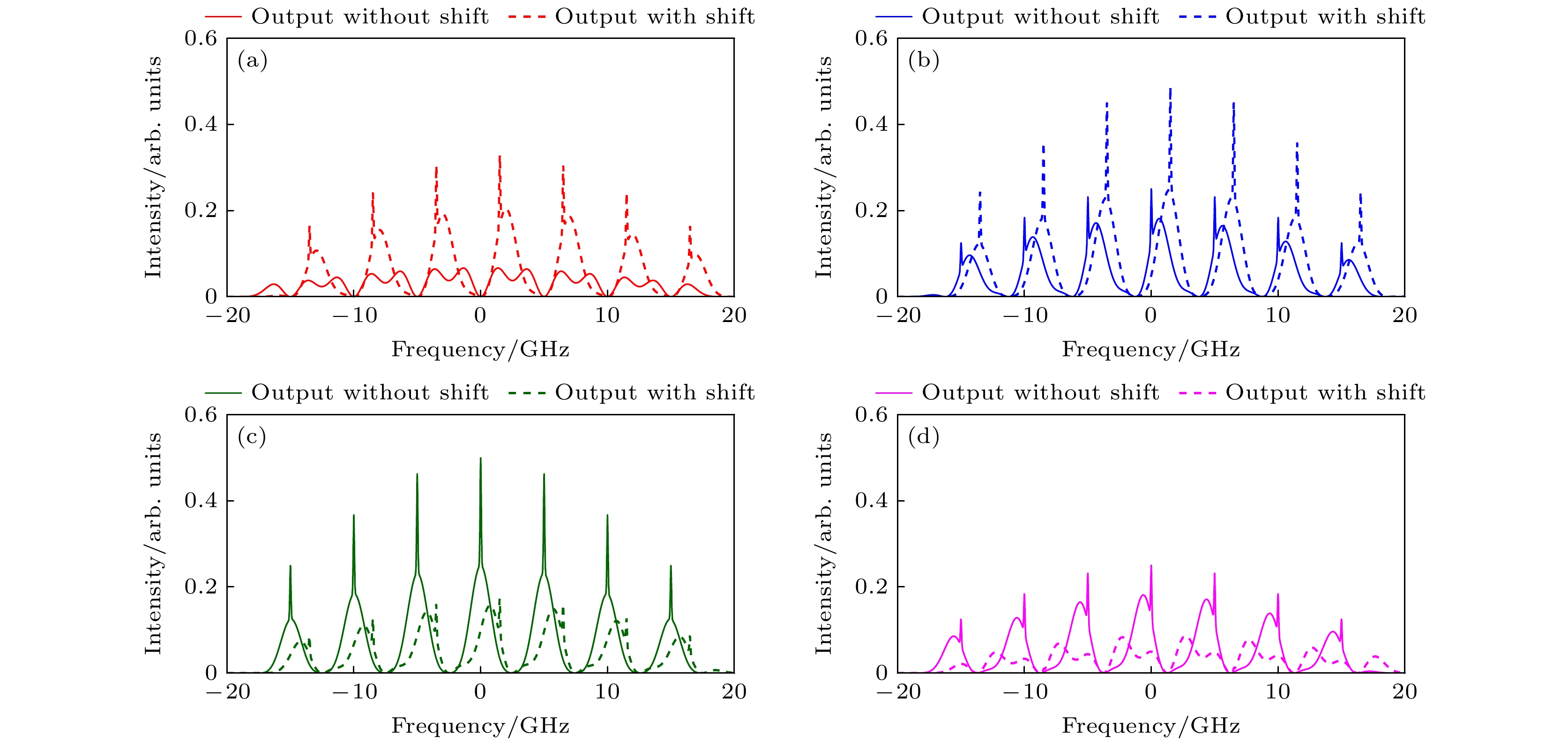
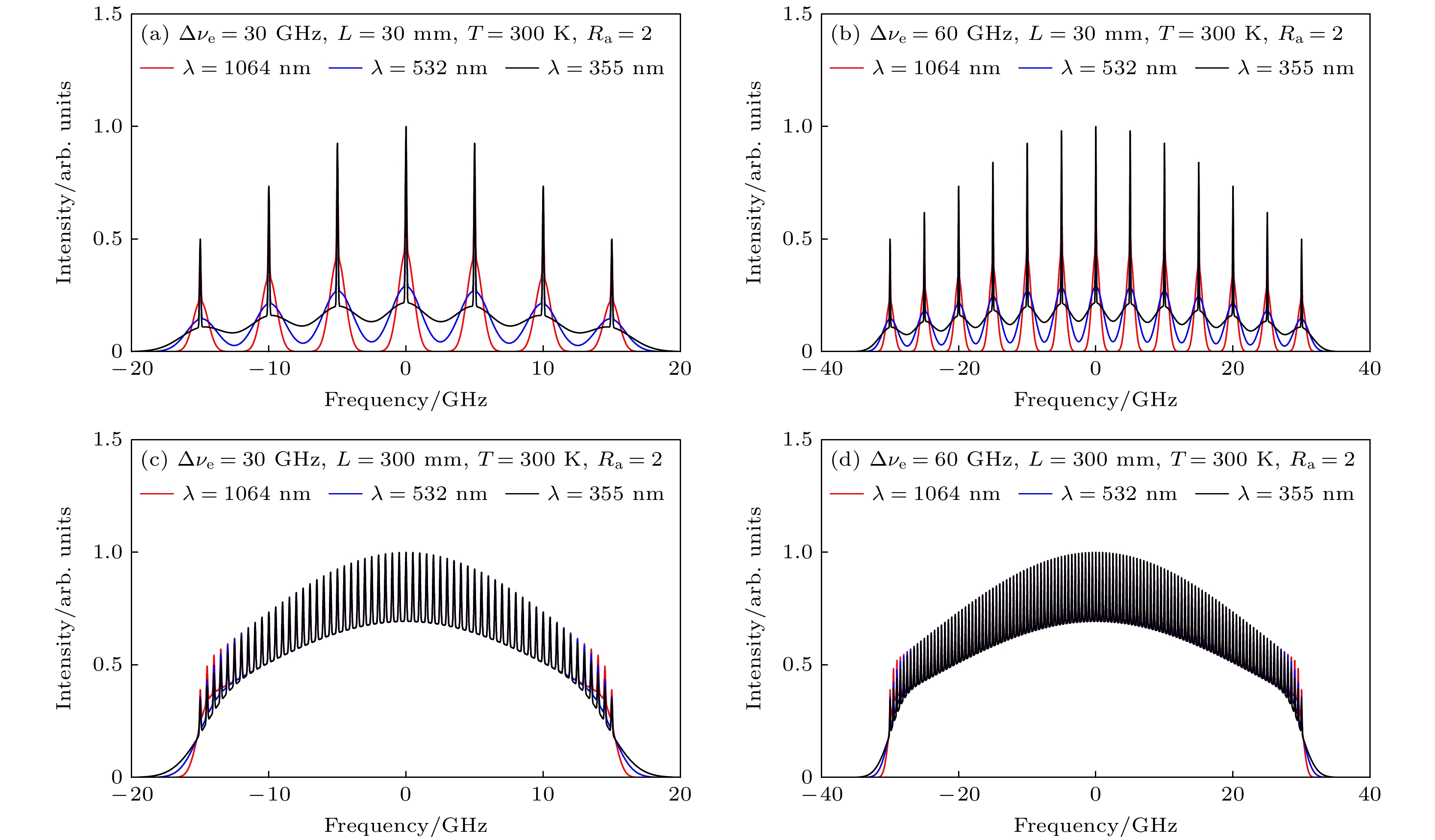
图 1 多纵模激光激励的大气弹性散射回波光谱示意图　(a) 激光辐射线宽为30 GHz, 激光光学谐振腔长为30 mm; (b) 激光辐射线宽为60 GHz, 激光光学谐振腔长为30 mm; (c) 激光辐射线宽为30 GHz, 激光光学谐振腔长为300 mm; (d) 激光辐射线宽为60 GHz, 激光光学谐振腔长为300 mm

Figure 1. Diagram of atmospheric elastic scattering echo spectra excited by multi-longitudinal mode laser: (a) Laser radiation linewidth is 30 GHz, laser optical resonator length is 30 mm; (b) laser radiation linewidth is 60 GHz, laser optical resonator length is 30 mm; (c) laser radiation linewidth is 30 GHz, laser optical resonator length is 300 mm; (d) laser radiation linewidth is 60 GHz, laser optical resonator length is 300 mm.

DownLoad: Full-Size Img PowerPoint

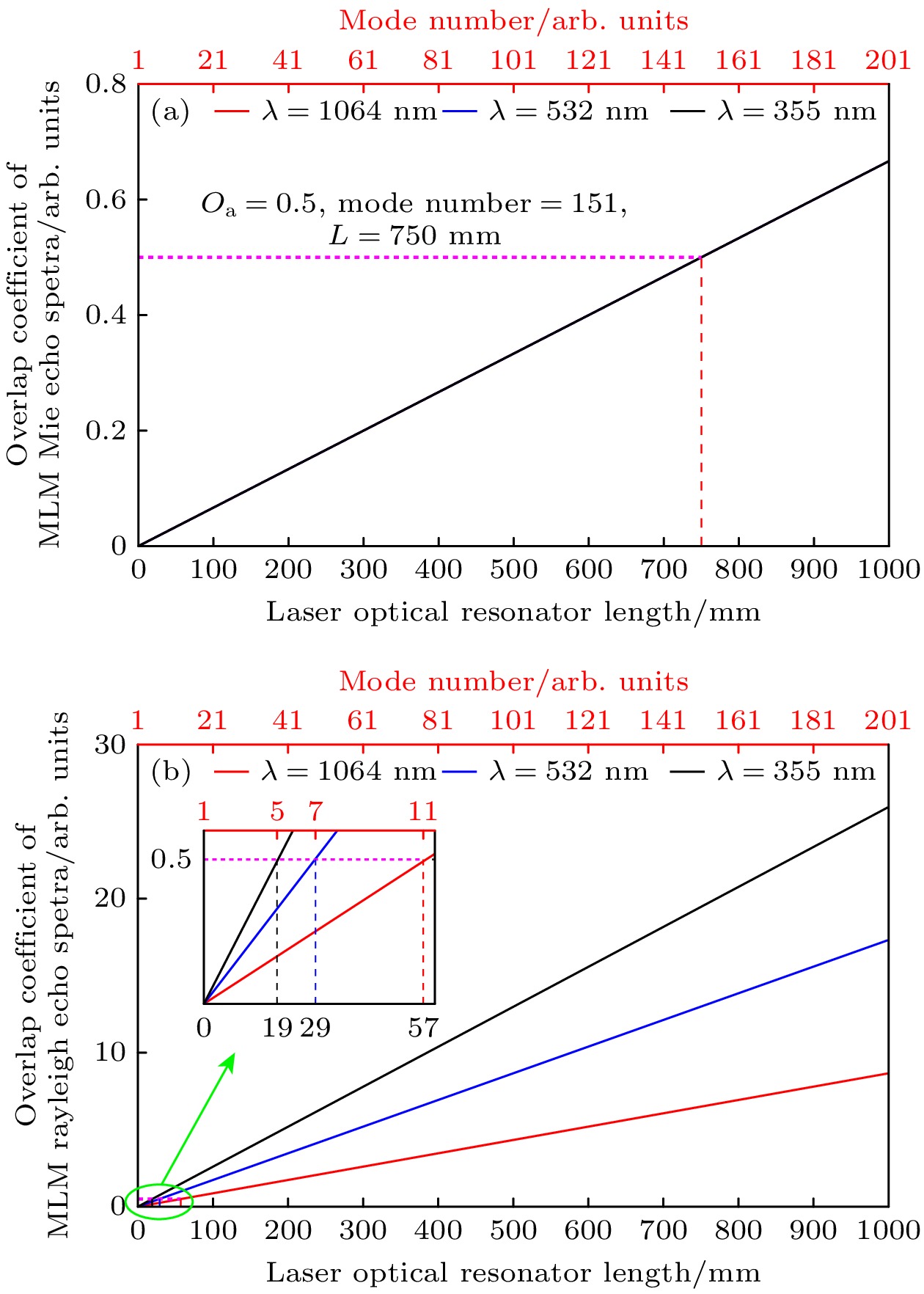
图 2 不同激光中心波长时, 交叠系数随激光光学谐振腔长的变化曲线　(a) 多纵模气溶胶米散射回波光谱的交叠系数; (b) 多纵模大气分子瑞利散射回波光谱的交叠系数

Figure 2. Change curve of overlap coefficient with laser optical resonator length under different laser center wavelengths: (a) Overlap coefficient of multi-longitudinal mode aerosol Mie scattering echo spectra; (b) overlap coefficient of multi-longitudinal mode molecular Rayleigh scattering echo spectra

DownLoad: Full-Size Img PowerPoint

图 3 直接单边缘检测技术鉴别多纵模大气弹性散射回波光谱多普勒频移的原理图

Figure 3. Principle diagram of direct single-edge detection technology for measuring the Doppler shift of atmospheric elastic scattering echo spetra excited by multi-longitudinal mode laser.

DownLoad: Full-Size Img PowerPoint

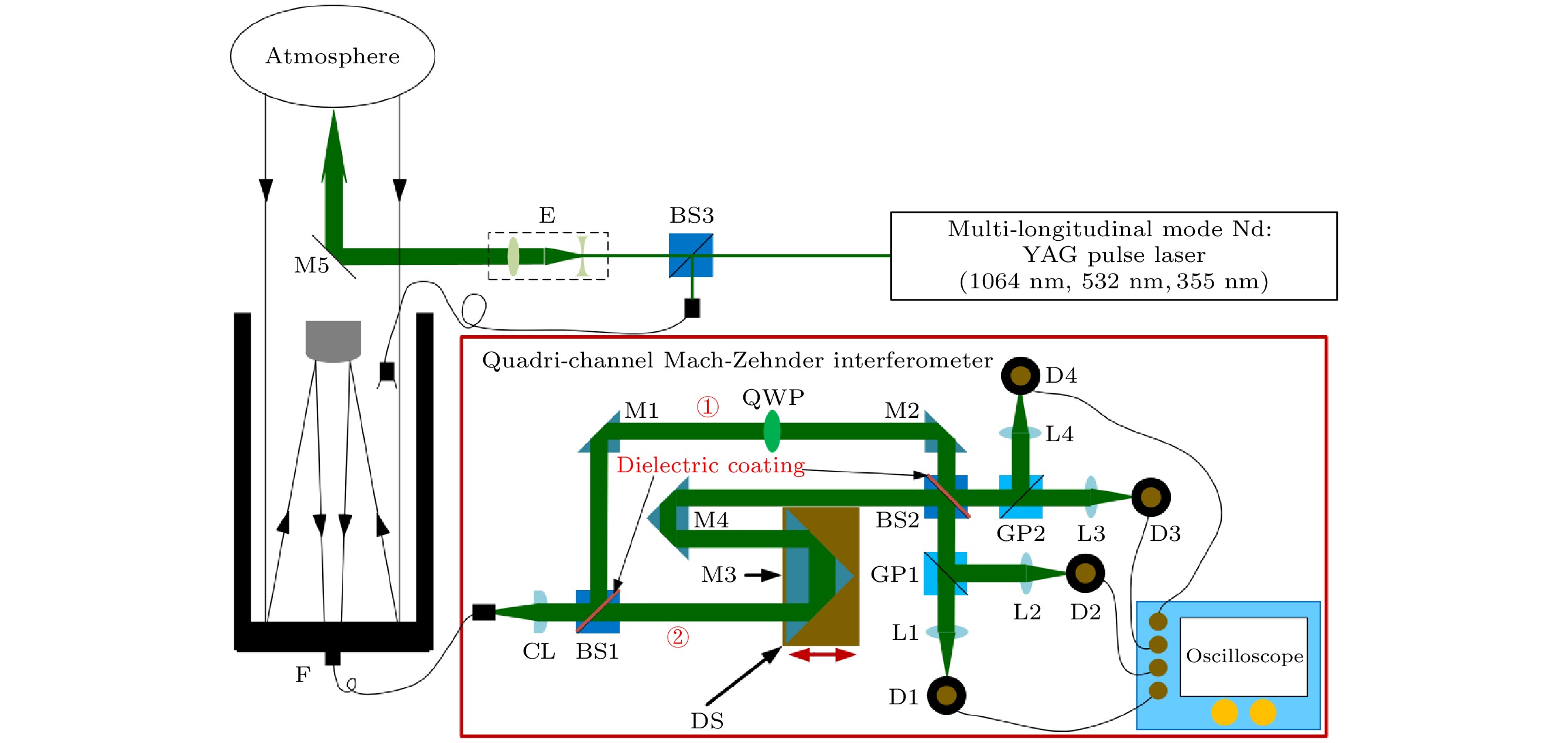
图 4 基于可调谐四通道马赫-曾德尔干涉仪的多纵模直接多普勒测风激光雷达系统图. BS: 光束分离器; E: 准直扩束器; M: 反射镜; F: 光纤; CL准直透镜; QWP: 四分之一波片; DS: 纳米位移系统; GP: 格兰棱镜; L: 汇聚透镜; D: 光电探测器件

Figure 4. System diagram of multi-longitudinal mode direct Doppler wind lidar based on quadri-channel Mach-Zehnder interferometer. BS: beam splitter; E: expander; M: mirror; F: fiber; CL: collimating lens; QWP: quarter-wave plate; DS: displacement system; GP: Glan prism; L: convergent lens; D: photoelectric detector.

DownLoad: Full-Size Img PowerPoint

图 5 四通道马赫-曾德尔干涉仪鉴别多纵模大气弹性散射回波光谱多普勒频移的原理图

Figure 5. Principle diagram of quadri-channel Mach-Zehnder interferometer for measuring Doppler shift of atmospheric elastic scattering echo spetra excited by multi-longitudinal mode laser.

DownLoad: Full-Size Img PowerPoint

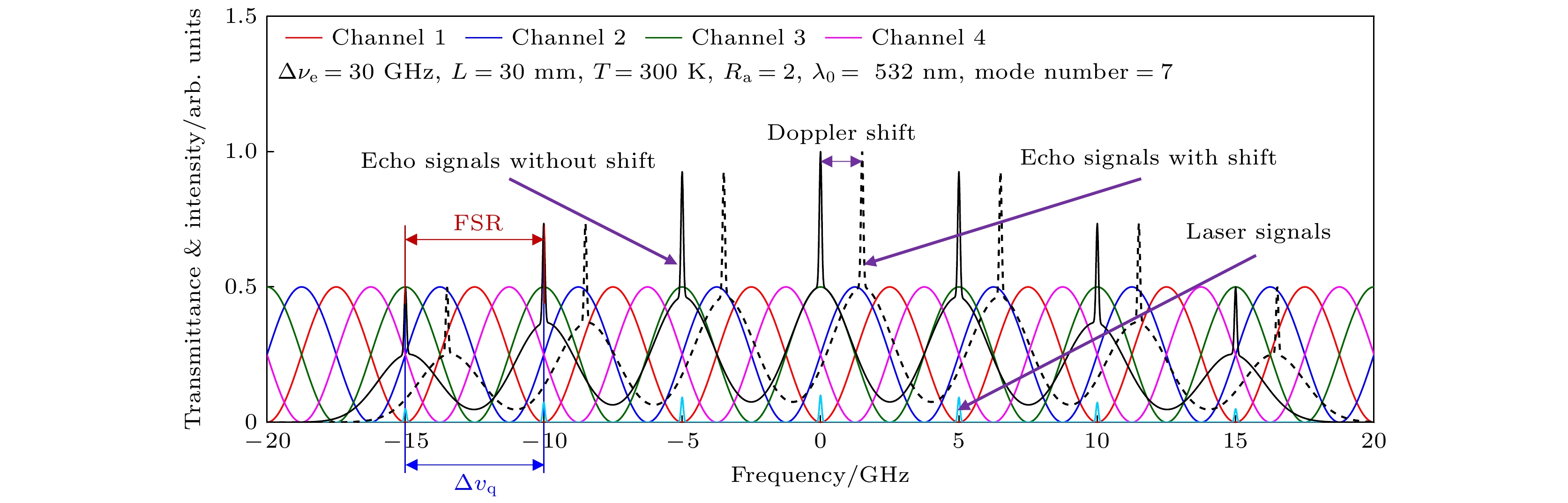
图 6 四通道马赫-曾德尔干涉仪鉴别多纵模大气弹性散射回波光谱多普勒频移的输出信号　(a) QMZI通道1输出信号; (b) QMZI通道2输出信号; (c) QMZI通道3输出信号; (d) QMZI通道4输出信号

Figure 6. Output signals of quadri-channel Mach-Zehnder interferometer for measuring Doppler shift of atmospheric elastic scattering echo spetra excited by multi-longitudinal mode laser: (a) Output signals of channel 1; (b) output signals of channel 2; (c) output signals of channel 3; (d) output signals of channel 4.

DownLoad: Full-Size Img PowerPoint

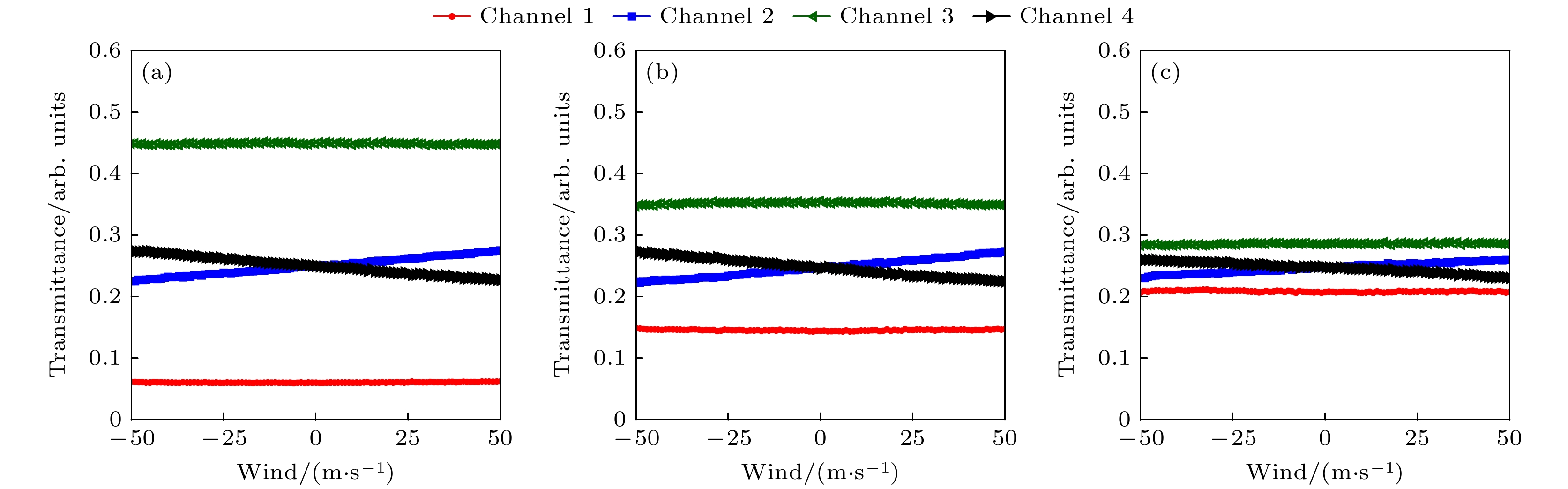
图 7 激光光学谐振腔长为30 mm时, 不同激光中心波长下QMZI有效透过率随风速变化的仿真曲线　(a) 激光中心波长为1064 nm; (b) 激光中心波长为532 nm; (c) 激光中心波长为355 nm

Figure 7. Simulation curve of effective transmittance of QMZI with wind speed at different laser center wavelengths when the laser optical resonator length is 30 mm: (a) The laser center wavelength is 1064 nm; (b) the laser center wavelength is 532 nm; (c) the laser center wavelength is 355 nm.

DownLoad: Full-Size Img PowerPoint

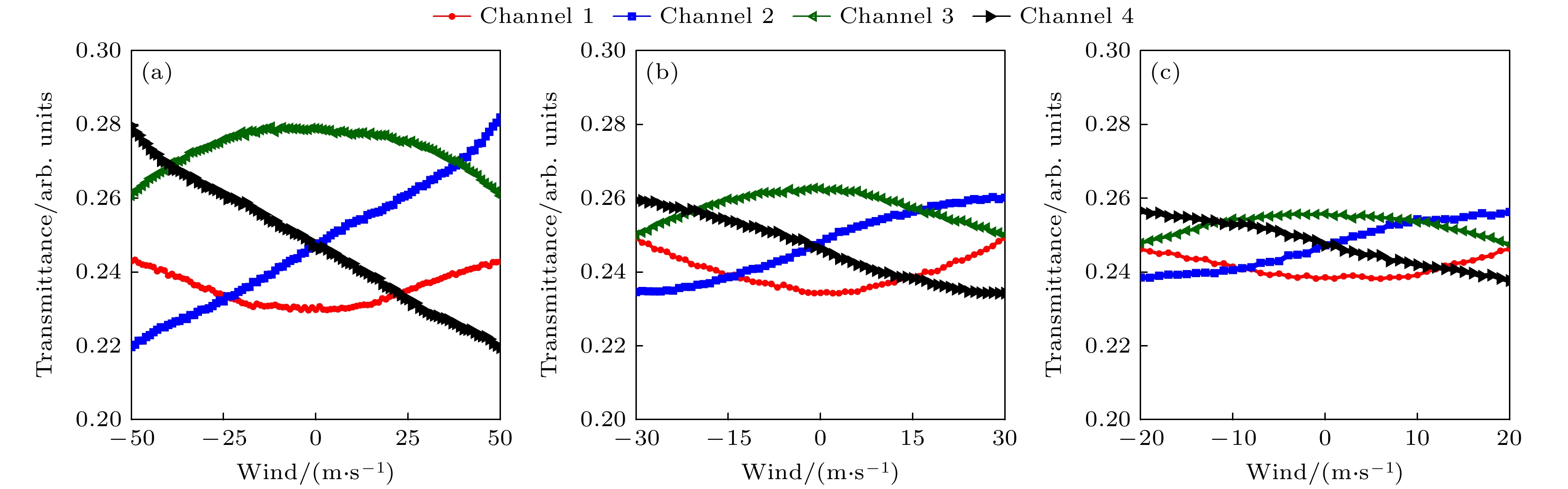
图 8 激光光学谐振腔长为300 mm时, 不同激光中心波长下QMZI有效透过率随风速变化的仿真曲线　(a) 激光中心波长为1064 nm; (b) 激光中心波长为532 nm; (c) 激光中心波长为355 nm

Figure 8. Simulation curve of effective transmittance of QMZI with wind speed at different laser center wavelengths when the laser optical resonator length is 300 mm: (a) The laser center wavelength is 1064 nm; (b) the laser center wavelength is 532 nm; (c) the laser center wavelength is 355 nm.

DownLoad: Full-Size Img PowerPoint

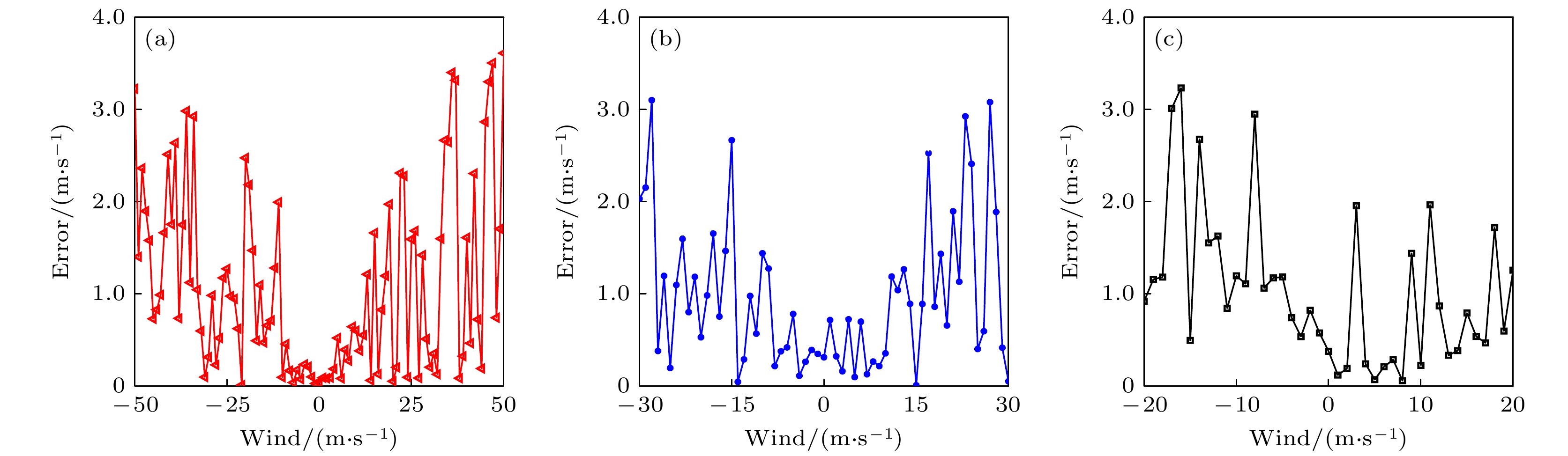
图 9 激光光学谐振腔长为30 mm时, 不同激光中心波长下多纵模直接多普勒测风激光雷达系统的测风误差随风速变化的仿真曲线　(a) 激光中心波长为1064 nm; (b) 激光中心波长为532 nm; (c) 激光中心波长为355 nm

Figure 9. Simulation curve of wind measurement error of multi-longitudinal mode direct Doppler wind lidar with wind speed at different laser center wavelengths when the laser optical resonator length is 30 mm: (a) The laser center wavelength is 1064 nm; (b) the laser center wavelength is 532 nm; (c) the laser center wavelength is 355 nm.

DownLoad: Full-Size Img PowerPoint

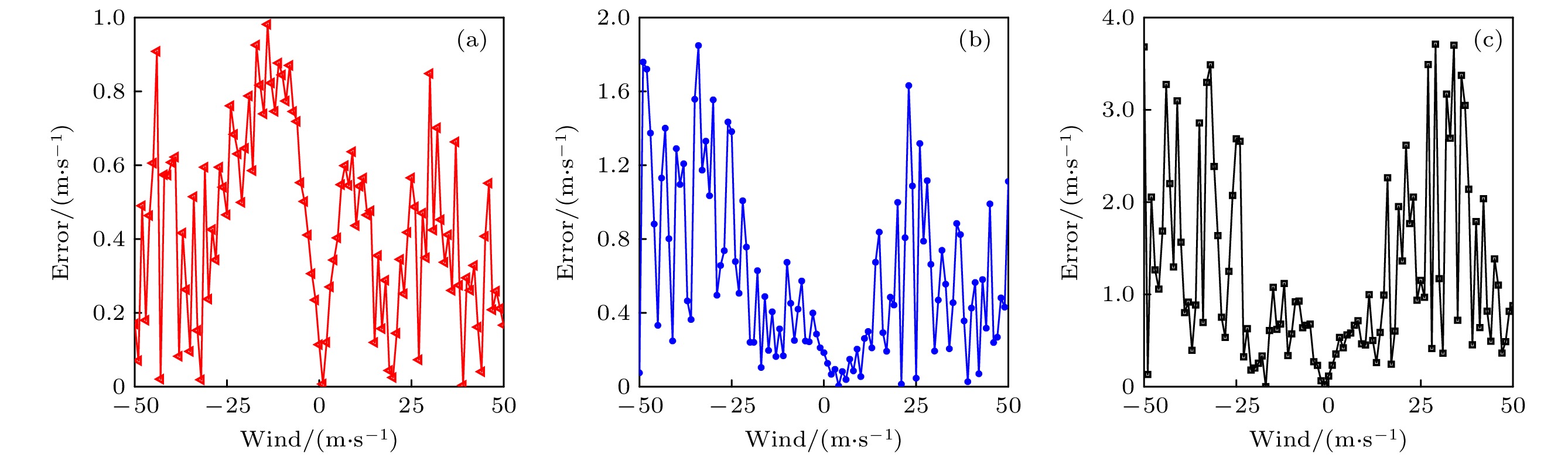
图 10 激光光学谐振腔长为300 mm时, 不同激光中心波长下多纵模直接多普勒测风激光雷达系统的测风误差随风速变化的仿真曲线　(a) 激光中心波长为1064 nm; (b) 激光中心波长为532 nm; (c) 激光中心波长为355 nm

Figure 10. Simulation curve of wind measurement error of multi-longitudinal mode direct Doppler wind lidar with wind speed at different laser center wavelengths when the laser optical resonator length is 300 mm: (a) The laser center wavelength is 1064 nm; (b) the laser center wavelength is 532 nm; (c) the laser center wavelength is 355 nm.

DownLoad: Full-Size Img PowerPoint

表 1 多纵模激光器体制下直接多普勒测风激光雷达关键参数.

Table 1. Key parameters of multi-longitudinal mode direct Doppler wind lidar.

参数	值	参数	值
激光中心波长/nm	1064, 532, 355	理论风速/(m·s^–1)	–50—50 (间隔1 m·s^–1)
激光辐射线宽/GHz	30	大气温度/K	300
激光光学谐振腔长/mm	30, 300	气溶胶后向散射比	2
激光纵模个数	7, 61	QMZI自由光谱范围/GHz	5.0, 0.5
激光纵模间隔/GHz	5.0, 0.5	—	—

DownLoad: CSV

map

[1]	Kumar D, Premachandran B 2019 Int. J. Therm. Sci. 138 263 Google Scholar
[2]	Liu G Q, Perrie W 2013 Geophys. Res. Lett. 40 3150 Google Scholar
[3]	Gardiner B, Berry P, Moulia B 2016 Plant Sci. 245 94 Google Scholar
[4]	Yu L J, Zhong S Y, Bian X D, Heilman W E 2018 Int. J. Climatol. 39 1684
[5]	马福民, 陈涌, 杨泽后, 周鼎富, 李晓锋, 陈春利, 冯力天, 余臣 2019 激光与光电子学进展 56 180003 Google Scholar Ma F M, Chen Y, Yang Z H, Zhou D F, Li X F, Chen C L, Feng L T, Yu C 2019 Laser Optoelectron. Prog. 56 180003 Google Scholar
[6]	Reitebuch O, Lemmerz Ch, Nagel E, Paffrath U, Durand Y, Endemann M, Fabre F, Chaloupy M 2009 J. Atmos. Oceanic Technol. 26 2501 Google Scholar
[7]	Paffrath U, Lemmerz Ch, Reitebuch O, Oliver, Witschas B, Nikolaus I, Freudenthaler V 2009 J. Atmos. Oceanic Technol. 26 2516 Google Scholar
[8]	储玉飞, 刘东, 王珍珠, 吴德成, 邓迁, 李路, 庄鹏, 王英俭 2020 量子电子学报 37 580 Chu Y F, Liu D, Wang Z Z, Wu D C, Deng Q, Li L, Zhuang P, Wang Y J 2020 Chin. J. Quantum Electron. 37 580
[9]	Jiang S, Sun D S, Han Y L, Han F, Zhou A R, Zheng J 2019 Curr. Opt. Photonics 3 466
[10]	Zhang Y P, Yuan J L, Wu Y B, Dong J J, Xia H Y 2023 Phys. Rev. Fluids 8 L022701 Google Scholar
[11]	Zhang Y P, Wu Y B, Dong J J, Xia H Y 2022 IEEE Photonics J. 14 6047706
[12]	Liu Z L, Barlow J F, Chan P W, Fung J C H, Li Y G, Ren C, Mark H W L, Ng E 2019 Remote Sens. 11 2522 Google Scholar
[13]	张亚飞, 冯玉涛, 傅頔, 畅晨光, 李娟, 白清兰, 胡炳樑 2022 71 084201 Google Scholar Zhang Y F, Feng Y T, Fu D, Chang C G, Li J, Bai Q L, Hu B J 2022 Acta Phys. Sin. 71 084201 Google Scholar
[14]	Vrancken P, Herbst J 2022 Remote Sens. 14 3356 Google Scholar
[15]	Kliebisch O, Uittenbosch H, Thurn J, Mahnke P 2022 Opt. Express 30 5540 Google Scholar
[16]	Wang L, Gao F, Wang J, Yan Q, Yan W X, Wang M, Hua D X 2019 Opt. Laser Eng. 121 61 Google Scholar
[17]	Hill C 2018 Remote Sens. 10 466 Google Scholar
[18]	Shen F H, Wang B X, Shi W J, Zhuang P, Zhu C Y, Xie C B 2018 Opt. Commun. 412 7 Google Scholar
[19]	潘艺升, 闫召爱, 郭文杰, 徐轻尘, 胡雄 2016 激光技术 40 153 Pan Y S, Yan Z A, Guo W J, Xu Q C, Hu X 2016 Laser Technol. 40 153
[20]	Wu C T, Chen F, Dai T Y, Ju Y L 2015 J. Mod. Opt. 62 1535 Google Scholar
[21]	张明富, 杨天新, 葛春风 2022 红外与激光工程 51 20210435 Google Scholar Zhang M F, Yang T X, Ge C F 2022 Infrared Laser Eng. 51 20210435 Google Scholar
[22]	葛烨, 胡以华, 舒嵘, 洪光烈 2015 64 020707 Google Scholar Ge Y, Hu Y H, Shu R, Hong G L 2015 Acta Phys. Sin. 64 020707 Google Scholar
[23]	Bruneau D, Blouzon F, Spatazza J, Montmessin F, Pelon J, Faure B 2013 Appl. Opt. 52 4941 Google Scholar
[24]	高飞, 南恒帅, 黄波, 汪丽, 李仕春, 王玉峰, 刘晶晶, 闫庆, 宋跃辉, 华灯鑫 2018 67 030701 Google Scholar Gao F, Nan H S, Huang B, Wang L, Li S C, Wang Y F, Liu J J, Yan Q, Song Y H, Hua D X 2018 Acta Phys. Sin. 67 030701 Google Scholar
[25]	Gao F, Nan H S, Zhang R, Zhu Q S, Chen T, Wang L, Chen H, Hua D X, Stanic S 2019 J. Quant. Spectrosc. Radiat. Transfer 234 10 Google Scholar
[26]	毛艳丽, 邱宏伟, 徐军, 邓佩珍, 干福熹 2001 光学学报 21 1264 Mao Y L, Qiu H W, Xu J, Deng P Z, Gan F X 2001 Acta Opt. Sin. 21 1264
[27]	Korb C L, Gentry B M, Weng C Y 1992 Appl. Opt. 31 4202 Google Scholar
[28]	Thompson B J, Wolf E 1957 J. Opt. Soc. Am. 47 895 Google Scholar

[1]	Ma Ping, Tian Jing, Tian De-Yang, Zhang Ning, Wu Ming-Xing, Tang Pu. A seven-channels microwave interferometer measurement system for measuring electron density distribution in hypervelocity transient plasma flow. Acta Physica Sinica, 2024, 73(17): 172401. doi: 10.7498/aps.73.20240656
[2]	Li Jun, Xue Zheng-Yue, Liu Xiao-Hai, Wang Jing-Jing, Wang Gui-Shi, Liu Kun, Gao Xiao-Ming, Tan Tu. Simulation of wind field detection by laser heterodyne spectrometer. Acta Physica Sinica, 2022, 71(7): 074204. doi: 10.7498/aps.71.20211252
[3]	Zhang Ya-Fei, Feng Yu-Tao, Fu Di, Chang Chen-Guang, Li Juan, Bai Qing-Lan, Hu Bing-Liang. Thermal imaging drift monitoring of Doppler asymmetric spatial heterodyne spectroscopy for wind measurement based on segmented edge fitting. Acta Physica Sinica, 2022, 71(8): 084201. doi: 10.7498/aps.71.20212086
[4]	Gao Fei, Nan Heng-Shuai, Huang Bo, Wang Li, Li Shi-Chun, Wang Yu-Feng, Liu Jing-Jing, Yan Qing, Song Yue-Hui, Hua Deng-Xin. Technical realization and system simulation of ultraviolet multi-mode high-spectral-resolution lidar for measuring atmospheric aerosols. Acta Physica Sinica, 2018, 67(3): 030701. doi: 10.7498/aps.67.20172036
[5]	Tang Yuan-He, Cui Jin, Gao Hai-Yang, Qu Ou-Yang, Duan Xiao-Dong, Li Cun-Xia, Liu Li-Na. Calibrations of ground based airglow imaging interferometer for the upper atmospheric wind field measurement. Acta Physica Sinica, 2017, 66(13): 130601. doi: 10.7498/aps.66.130601
[6]	Zhang Ri-Wei, Sun Xue-Jin, Yan Wei, Zhao Jian, Liu Lei, Li Yan, Zhang Chuan-Liang, Zhou Jun-Hao. Simulation of frequency discrimination for spaceborne Doppler wind lidar (Ⅱ)：Study on the retrieval of atmospheric wind speed for Rayleigh channel based on Fabry-Perot interferometer. Acta Physica Sinica, 2014, 63(14): 140703. doi: 10.7498/aps.63.140703
[7]	Jiang Zhu-Hui, Zhou Xiao-Zhong, You Xiao-Bao, Yi Xin, Huang Wei-Quan. Analysis on the variational model of synthetic aperture radar sea surface wind retrieval. Acta Physica Sinica, 2014, 63(14): 148401. doi: 10.7498/aps.63.148401
[8]	Tan Lin-Qiu, Hua Deng-Xin, Wang Li, Gao Fei, Di Hui-Ge. Wind velocity retrieval and field widening techniques of fringe-imaging Mach-Zehnder interferometer for Doppler lidar. Acta Physica Sinica, 2014, 63(22): 224205. doi: 10.7498/aps.63.224205
[9]	Zhang Ri-Wei, Sun Xue-Jin, Yan Wei, Liu Lei, Li Yan, Zhao Jian, Yan Wan-Xiang, Li Hao-Ran. Simulation of frequency discrimination for spaceborne Doppler wind lidar (I)：Study on the retrieval of atmospheric wind speed for Mie channel based on Fizeau interferometer. Acta Physica Sinica, 2014, 63(14): 140702. doi: 10.7498/aps.63.140702
[10]	Ai Wei-Hua, Yan Wei, Zhao Xian-Bin, Liu Wen-Jun, Ma Shuo. A new ocean surface wind field retrieval method from C-band airborne synthetic aperture radar. Acta Physica Sinica, 2013, 62(6): 068401. doi: 10.7498/aps.62.068401
[11]	Shen Fa-Hua, Sun Dong-Song, Liu Cheng-Lin, Qiu Cheng-Qun, Shu Zhi-Feng. Data inversion technique for single Fabry-Perot etalon-based dual-frequency Doppler lidar. Acta Physica Sinica, 2013, 62(22): 220702. doi: 10.7498/aps.62.220702
[12]	Zhang Xuan-Ni, Zhang Chun-Min, Ai Jing-Jing. The signal-to-noise ratio of the quarter beam of wind imaging polarization interferometer. Acta Physica Sinica, 2013, 62(3): 030701. doi: 10.7498/aps.62.030701
[13]	Dai Hai-Shan, Zhang Chun-Min, Mu Ting-Kui. Research of secondary fringes in field-widened achromatic, temperature-compensated wind, imaging interferometer (FATWindII). Acta Physica Sinica, 2012, 61(22): 224201. doi: 10.7498/aps.61.224201
[14]	Shen Fa-Hua, Shu Zhi-Feng, Sun Dong-Song, Wang Zhong-Chun, Xue Xiang-Hui, Chen Ting-Di, Dou Xian-Kang. Improvement of wind retrieval algorithm for Rayleigh Doppler lidar. Acta Physica Sinica, 2012, 61(3): 030702. doi: 10.7498/aps.61.030702
[15]	Jiang Zhu-Hui, Huang Si-Xun, He Ran, Zhou Chen-Teng. Regularization method to retrieve synthetic aperture radar sea surface wind. Acta Physica Sinica, 2011, 60(6): 068401. doi: 10.7498/aps.60.068401
[16]	Han Kui, Wang Zi-Yu, Shen Xiao-Peng, Wu Qiong-Hua, Tong Xing, Tang Gang, Wu Yu-Xi. Mach-Zehnder interferometer designed based on self-collimating beams and photonic band gap in photonic crystals. Acta Physica Sinica, 2011, 60(4): 044212. doi: 10.7498/aps.60.044212
[17]	Zhu Hua-Chun, Zhang Chun-Min. Theoretical study of polarization atmosphere Michelsoninterferometer using multi-wavelength. Acta Physica Sinica, 2011, 60(7): 074211. doi: 10.7498/aps.60.074211
[18]	Shu Zhi-Feng, Dou Xian-Kang, Wang Zhong-Chun, Shen Fa-Hua, Sun Dong-Song, Xue Xiang-Hui, Chen Ting-Di. Wind retrieval algorithm of Rayleigh Doppler lidar. Acta Physica Sinica, 2011, 60(6): 060704. doi: 10.7498/aps.60.060704
[19]	Wang Jin-Chan, Zhang Chun-Min, Zhao Bao-Chang, Liu Ning. Study on the rule of light transmission through the four-sided pyramid prism in the static polarization wind imaging interferometer. Acta Physica Sinica, 2010, 59(3): 1625-1631. doi: 10.7498/aps.59.1625
[20]	Tang Yuan-He, Zhang Chun-Min, Liu Han-Chen, Chen Guang-De, He Jian. Study of the technique of 4-face coated pyramid prism for measurement of upper atmospheric wind field. Acta Physica Sinica, 2005, 54(9): 4065-4071. doi: 10.7498/aps.54.4065

Catalog

Vol. 73, Issue 20 - 2024-10-20

Metrics

Abstract views: 562
PDF Downloads: 22
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板