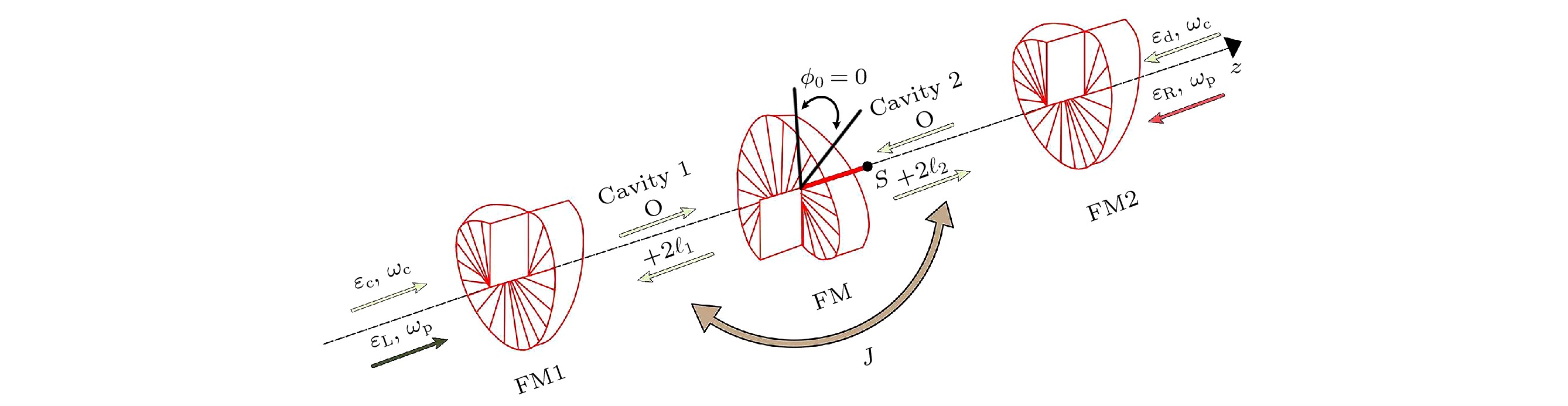
图 1  双拉盖尔-高斯旋转腔示意图, 两L-G腔场通过光旋转相互作用与中间的旋转腔镜耦合, 振幅为$ {\varepsilon _{\text{c}}} $和$ {\varepsilon _{\text{d}}} $($ {\varepsilon _{\text{L}}} $和$ {\varepsilon _{\text{R}}} $)的强驱动场(弱探测场)分别从两侧入射系统来驱动L-G腔模$ {c_1} $和$ {c_{\text{2}}} $, 同时用光纤将两L-G腔模线性耦合. 旋转腔镜的平衡位置为$ {\phi _{\text{0}}} $, 在扭力作用下的角位移用$ \phi $角表示

Fig. 1.  Schematic diagram of double Laguerre-Gaussian (L-G) rotational-cavity. The two L-G cavity modes are coupled with a rotating cavity mirror in the middle via the optical rotation interaction. Two strong pump fields (weak probe fields) with amplitudes $ {\varepsilon _{\text{c}}} $ and $ {\varepsilon _{\text{d}}} $ ($ {\varepsilon _{\text{L}}} $ and $ {\varepsilon _{\text{R}}} $) are incident on the system from both sides to drive the L-G cavity modes $ {c_1} $ and $ {c_{\text{2}}} $, and the two L-G cavity modes are linearly coupled with an optical fiber. The equilibrium position of the rotational mirror is $ {\phi _{\text{0}}} $, and the angular displacement is indicated by angle $ \phi $ under the action of the torsion.

图 2  传输振幅$ {T_{12}} $(红色实线)和$ {T_{21}} $(蓝色虚线)在不同非互易相位差$ \theta $下随标准化失谐$ x/{\kappa _1} $的演化　(a) $ \theta = 0 $; (b) $ \theta = - {\text{π }}/4 $; (c) $ \theta = {\text{π }}/4 $; (d) $ \theta = - {\text{π }}/2 $; (e) $ \theta = {\text{π }}/2 $. (f)在标准化失谐为零(x = 0)时, 传输振幅$ {T_{12}} $(红色实线)和$ {T_{21}} $(蓝色虚线)随非互易相位差$ \theta $的演化. 其他参数为$ {\kappa _1} = 1 $, $ {\kappa _2} = 1 $, $ \gamma = 1 $, $ {G_i} = \sqrt {{\kappa _i}\gamma } /2 $, $ J = \sqrt {{\kappa _1}{\kappa _2}} /2 $.

Fig. 2.  Transmission amplitudes $ {T_{12}} $ (red solid line) and $ {T_{21}} $ (blue dotted line) versus normalized detuning $ x/{\kappa _1} $ under different nonreciprocal phase difference: (a) $ \theta = 0 $; (b) $ \theta = - {\text{π }}/4 $; (c) $ \theta = {\text{π }}/4 $; (d) $ \theta = - {\text{π }}/2 $; (e) $ \theta = {\text{π }}/2 $. (f) Transmission amplitudes $ {T_{12}} $ (red solid line) and $ {T_{21}} $ (blue dotted line) versus nonreciprocal phase difference with $ x = 0 $. Other parameters are $ {\kappa _1} = 1 $, $ {\kappa _2} = 1 $, $ \gamma = 1 $, $ {G_i} = \sqrt {{\kappa _i}\gamma } /2 $, $ J = \sqrt {{\kappa _1}{\kappa _2}} /2 $.

图 3  (a)传输振幅$ {T_{12}} $和(b)传输振幅$ {T_{{\text{21}}}} $作为标准化失谐$ x/{\kappa _1} $和旋转镜与腔$ {c_1} $耗散比$ \gamma /{\kappa _1} $的函数; (c)传输振幅$ {T_{12}} $和(d)传输振幅$ {T_{{\text{21}}}} $作为标准化失谐$ x/{\kappa _1} $和腔$ {c_2} $与腔$ {c_1} $耗散比$ {\kappa _2}/{\kappa _1} $的函数. 其他参数为$ \theta = {\text{π }}/2 $, $ {\kappa _1} = 1 $, $ {G_1} = {G_2} = J = 1/2 $

Fig. 3.  (a) Transmission amplitude $ {T_{12}} $ and (b) transmission amplitude $ {T_{21}} $ as a function of the normalized detuning $ x/{\kappa _1} $ and the dissipation ratio $ \gamma /{\kappa _1} $ of rotating mirror to cavity $ {c_1} $; (c) transmission amplitudes $ {T_{12}} $ and (d) transmission amplitudes $ {T_{21}} $ as a function of the normalized detuning $ x/{\kappa _1} $ and the dissipation ratio $ {\kappa _2}/{\kappa _1} $ of cavity $ {c_2} $ to cavity $ {c_1} $. Other parameters are $ \theta = {\text{π }}/2 $, $ {\kappa _1} = 1 $, $ {G_1} = {G_2} = J = 1/2 $.

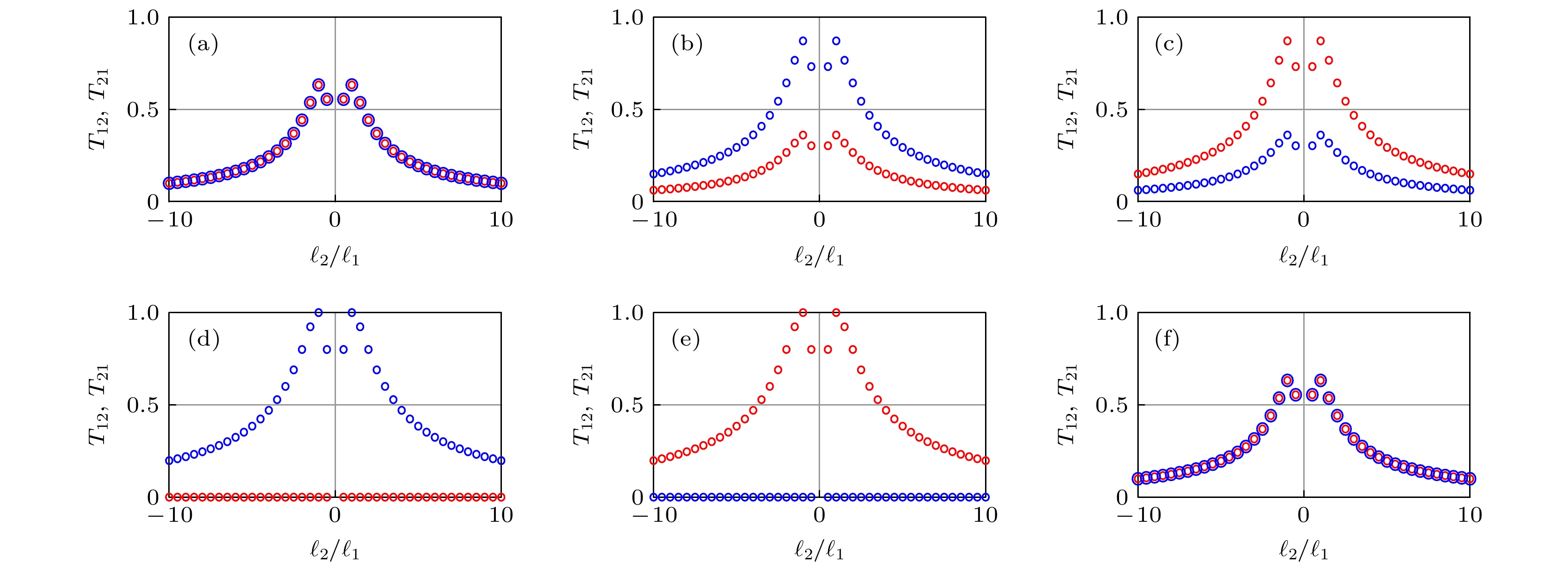
图 4  传输振幅$ {T_{12}} $(红色圆圈)和$ {T_{21}} $(蓝色圆圈)在不同非互易相位差$ \theta $下随两个涡旋光场所携带拓扑荷之比$ {\ell _2}/{\ell _1} $的演化　(a) $\theta = 0$; (b) $ \theta = - {\text{π }}/4 $; (c) $ \theta = {\text{π }}/4 $; (d) $ \theta = - {\text{π }}/2 $; (e) $ \theta = {\text{π }}/2 $; (f) $ \theta = {\text{π }} $. 其他参数为$ {\kappa _1} = 1 $, $ {\kappa _2} = 1 $, $ \gamma = 1 $, $ J = 2{G_1}{G_2}/\gamma $

Fig. 4.  Transmission amplitudes $ {T_{12}} $ (red circle) and $ {T_{21}} $ (blue circle) with ratio of topological charges carried by two vortex optical fields $ {\ell _2}/{\ell _1} $ under different nonreciprocal phase difference: (a) $ \theta = 0 $; (b)$ \theta = - {\text{π }}/4 $; (c)$ \theta = {\text{π }}/4 $; (d) $ \theta = - {\text{π }}/2 $; (e) $ \theta = {\text{π }}/2 $; (f) $ \theta = {\text{π }} $. Other parameters are $ {\kappa _1} = 1 $, $ {\kappa _2} = 1 $, $ \gamma = 1 $, $ J = 2{G_1}{G_2}/\gamma $.

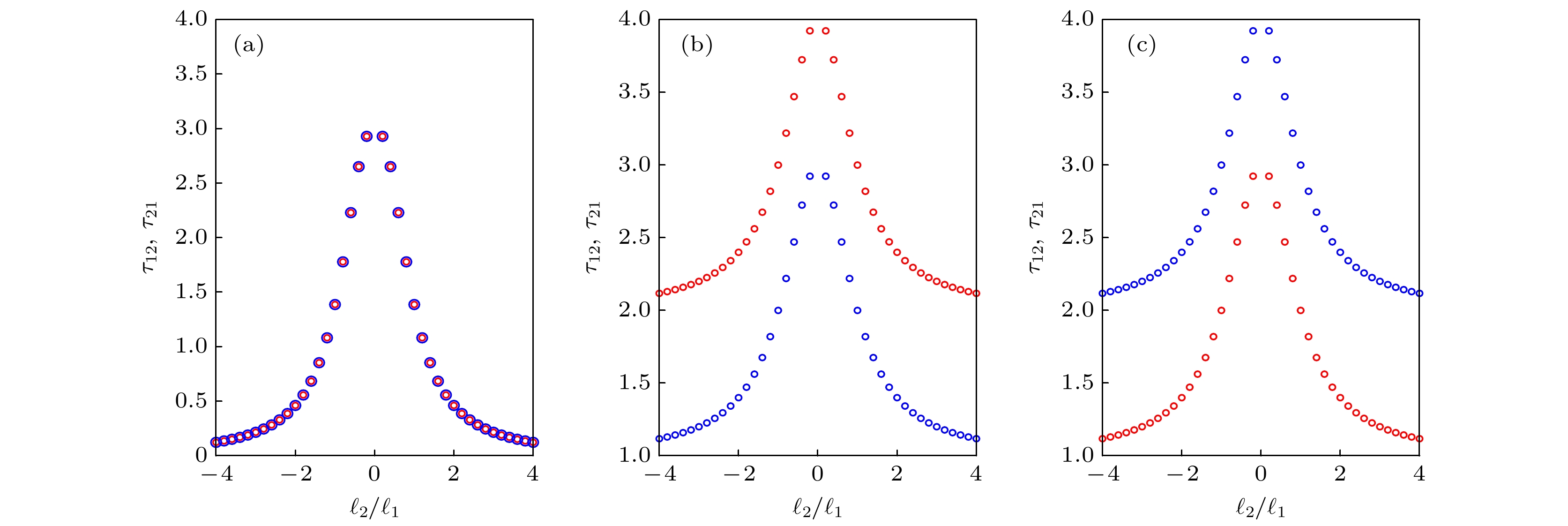
图 5  群延迟$ {\tau _{12}} $(红色圆圈)和$ {\tau _{21}} $(蓝色圆圈)在不同非互易相位差$ \theta $下随两个涡旋光场所携带拓扑荷比$ {\ell _2}/{\ell _1} $的演化　(a) $\theta = 0$; (b) $ \theta = - {\text{π }}/2 $; (c) $ \theta = {\text{π }}/2 $. 其他参数为$ {\kappa _1} = 1 $, $ {\kappa _2} = 1 $, $ \gamma = 1 $, $ J = 2{G_1}{G_2}/\gamma $

Fig. 5.  Group delay $ {\tau _{12}} $ (red circle) and $ {\tau _{21}} $ (blue circle) with ratio of topological charges carried by two vortex optical fields $ {\ell _2}/{\ell _1} $ under different nonreciprocal phase difference: (a) $ \theta = 0 $; (b) $ \theta = - {\text{π }}/2 $; (c) $ \theta = {\text{π }}/2 $. Other parameters are $ {\kappa _1} = 1 $, $ {\kappa _2} = 1 $, $ \gamma = 1 $, $ J = 2{G_1}{G_2}/\gamma $.