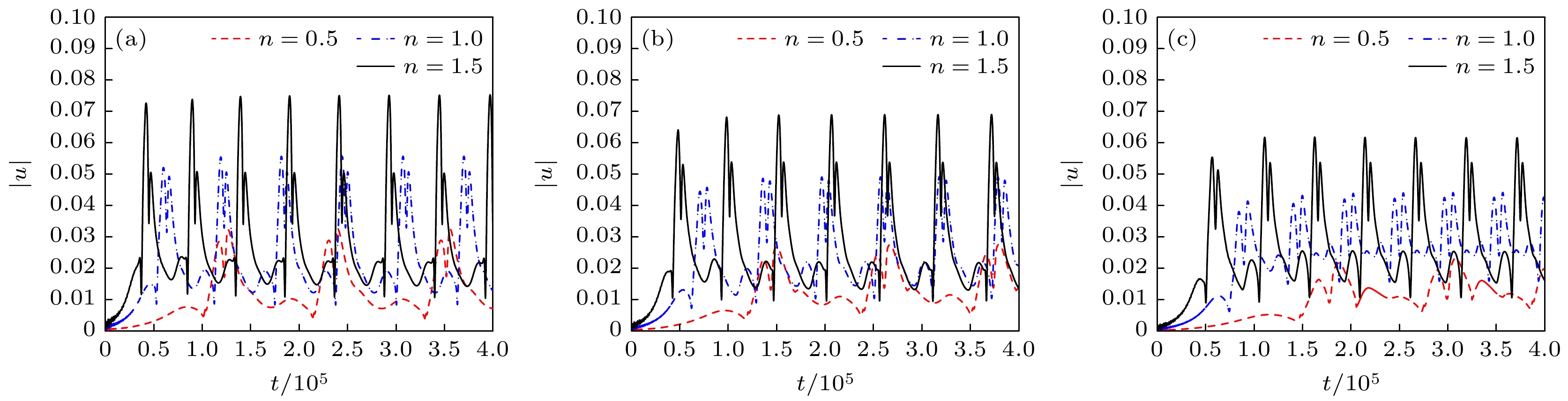
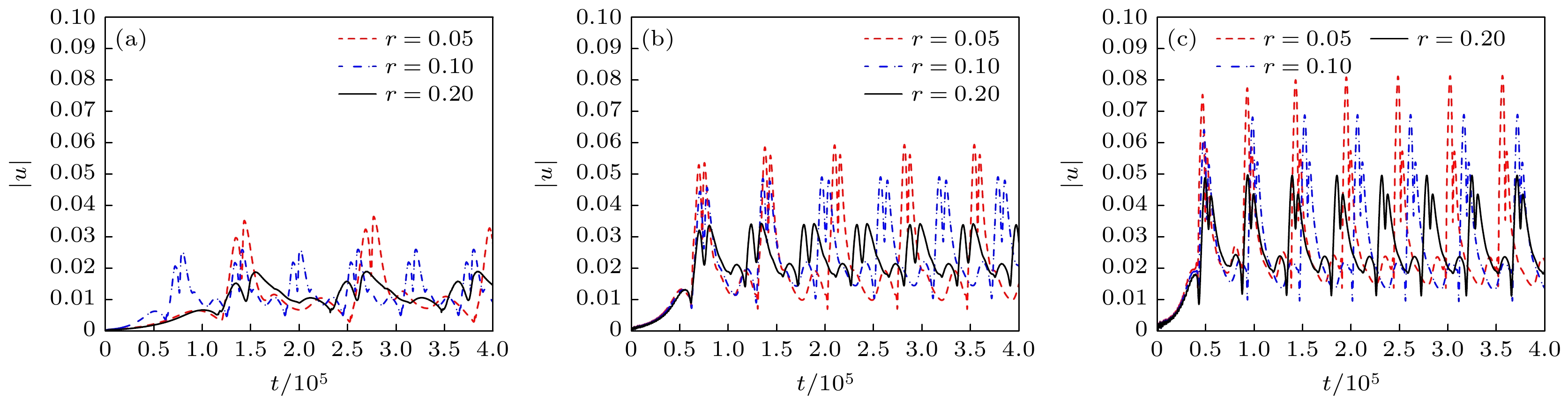
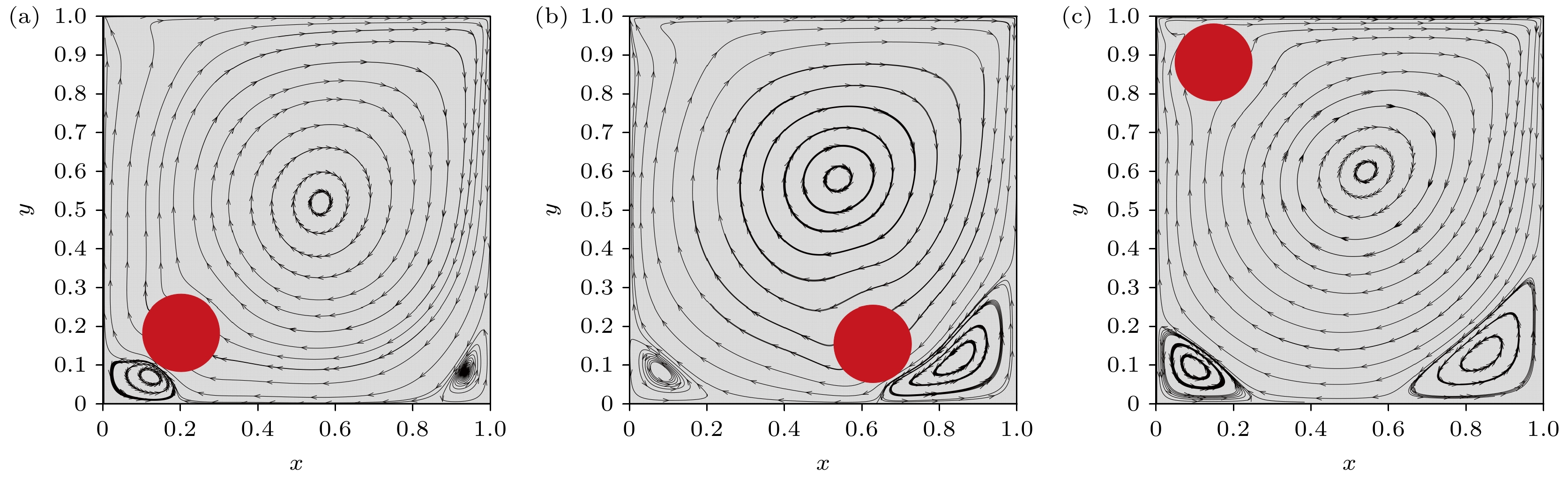
-
In this paper, the motion of a circular particle in a lid-driven square cavity with the power-law fluid is studied by using the diffuse interface lattice Boltzmann method, and the study mainly considers the effects of the particle's initial position, the power-law index, the Reynolds number, and the particle size. The numerical results show that the circular particle is first in a centrifugal motion under the effect of inertia, and it finally moves steadily on the limit cycle. Furthermore, it is also found that the initial position of the particle has no influence on the limit cycle. For a shear-thinning fluid flow, the limit cycle moves towards the bottom right corner of the square cavity. Moreover, the particle velocity is small, and the period of the particle motion is long. On the other hand, in the case of shear-thickening fluid flow, the limit cycle moves towards the top left corner of the cavity. In addition, the particle velocity is large, and the period of the particle motion is short.With the increase of Reynolds number, the limit cycle moves towards the bottom right corner of the square cavity, which is caused by a strong fluid flow field. Meanwhile, the particle velocity becomes larger, and the period of the particle motion is shorter. With the increase of particle size, the effect of confinement of the cavity boundary becomes significant, and the circular particle is pushed towards the center of the cavity. In this case, the limit cycle shrinks towards the center of the cavity. The circular particle squeezes the secondary vortices, especially when the circular particle is located in the bottom left, bottom right and top left corners. Additionally, the appearance of the circular particle has a significant influence on the position of the primary vortex, which changes periodically near the position of the primary vortex without the particle. It is also observed that the influence of the circular particle becomes more significant as its size increases and the power-law index decreases.
-
Keywords:
- lattice Boltzmann method /
- circular particle /
- power-law /
- lid-driven cavity
[1] Chhabra R P 2006 Bubbles, Drops, and Particles in Non-Newtonian Fluids (Boca Raton: CRC Press) pp40-74
[2] 朱克勤 2006 力学与实践 28 1
Google Scholar
Zhu K Q 2006 Mech. Eng. 28 1
Google Scholar
[3] Saramito P, Roquet N 2001 Comput. Methods Appl. Mech. Eng. 190 5391
Google Scholar
[4] Neofytou P 2005 Adv. Eng. Software 36 664
Google Scholar
[5] Rafiee A 2008 Anziam J. 49 411
Google Scholar
[6] Bell B C, Surana K S 1994 Int. J. Numer. Methods Fluids 18 127
Google Scholar
[7] Papanastasiou T C, Boudouvis A G 1997 Comput. Geotech. 64 677
[8] Papanastasiou T C 1987 J. Rheol. 31 385
Google Scholar
[9] Roquet N, Saramito P 2008 J. Non-Newtonian Fluid Mech. 155 101
Google Scholar
[10] Tazangi H R, Goharrizi A S, Javaran E J 2021 Korea-Aust. Rheol. J. 33 293
Google Scholar
[11] Schreiber R, Keller H B 1983 J. Comput. Phys. 49 310
Google Scholar
[12] Botella O, Peyret R 1998 Comput. Fluids 27 421
Google Scholar
[13] Erturk E, Corke T C 2005 Int. J. Numer. Methods Fluids 48 747
Google Scholar
[14] Mendu S S, Das P K 2012 J. Non-Newtonian Fluid Mech. 175–176 10
[15] Li Q X, Hong N, Shi B C, Chai Z H 2014 Commun. Comput. Phys. 15 265
Google Scholar
[16] Aguirre A, Castillo E, Cruchaga M, Codina R, Baiges J 2018 J. Non-Newton. Fluid Mech. 257 22
Google Scholar
[17] Alleborn N, Raszillier H, Durst F 1999 Int. J. Heat Mass Trans. 42 833
Google Scholar
[18] Stephen T, Nathan E 2007 Geology 35 1027
[19] Zhong H C, Zhou J, Du Z X, Xie L 2018 J. Aerosol Sci. 121 31
Google Scholar
[20] Madankan R, Pouget S, Singla P, Bursik M, Dehn J, Jones M, Patra A, Pavolonis M, Pitman E B, Singh T, Webley P 2014 J. Comput. Phys. 271 39
Google Scholar
[21] Yue G X, Cai R X, Lu J F, Zhang H 2017 Powder Technol. 316 18
Google Scholar
[22] He W C, Lv X W, Pan F F, Li X Q, Yan Z M 2019 Powder Technol. 356 1087
Google Scholar
[23] Sidik N A C, Attarzadeh S M R 2011 Int. J. Mech. 5 123
[24] Romanò F, Kuhlmann H C 2017 Theor. Comput. Fluid Dyn. 31 427
Google Scholar
[25] Hu J J, Sun D K, Mao S H, Wu H M, Yu S Y, Xu M S 2022 J. Comput. Theor. Transp. 51 222
Google Scholar
[26] Hu J J 2021 Int. J. Mod. Phys. C 32 1
[27] Hu J J 2020 Phys. Fluids 32 222
[28] Safdari A, Kim K C 2014 Comput. Math. Appl. 68 606
Google Scholar
[29] Francescò R, Hendrik H C 2017 Theor. Comput. Fluid Dyn. 31 1
[30] Chen S, Doolen G D 1998 Rev. Fluid Mech. 30 329
Google Scholar
[31] Succi S 2001 The Lattice Boltzmann Equation for Fluid Dynamics and Beyond (Oxford: Oxford University Press) pp3-38
[32] Guo Z L, Shu C 2013 Lattice Boltzmann Method and Its Applications in Engineering (Singapore: World Scientific Publishing Co.) pp10-21
[33] Krüger T, Kusumaatmaja H, Silva G, Shardt O, Kuzmin A, Viggen E M 2017 The Lattice Boltzmann Method: Principles and Practice (Switzerland: Springer International Publishing) pp61-65
[34] Feng J, Hu H H, Joseph D D 1994 J. Fluid Mech. 277 271
Google Scholar
[35] Inamuro T, Maeba K, Ogino F 2000 Int. J. Multiphase. Flow 26 1981
Google Scholar
[36] Shao X, Yu Z, Sun B 2008 Phys. Fluids 20 103307
Google Scholar
[37] Noble D R, Torczynski J R 1998 Int. J. Modern Phys. C 9 1189
Google Scholar
[38] Liu J, Huang C S, Chai Z H, Shi B C 2022 Comput. Fluids 233 105240
Google Scholar
[39] Liu J, Chai Z H, Shi B C 2022 Phys. Rev. E 106 015306
Google Scholar
[40] Boyd J, Buick J, Green S 2006 J. Phys. A 39 14241
Google Scholar
[41] Tang G H, Li X F, He Y L, Tao W Q 2009 J. Non-Newton. Fluid Mech. 157 133
Google Scholar
[42] Chai Z H, Shi B C, Guo Z L, Rong F M 2011 J. Non-Newton. Fluid Mech. 166 332
Google Scholar
[43] Guo Z L, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
-
图 1 不同幂律指数下的中心线速度分布($ Re = 100 $) (a)垂直速度; (b) 水平速度
Figure 1. The velocity profiles along the centerlines at different power-law indices ($ Re = 100 $): (a) The vertical velocity profile; (b) the horizontal velocity profile.
图 2 圆形颗粒在顶盖驱动流中运动的示意图
Figure 2. The schematic of a circular particle moving in a lid-driven square cavity.
图 3 不同雷诺数下圆形颗粒的极限环
Figure 3. The limit cycles of a circular particle at different Reynolds numbers.
图 4 $ Re = 1000 $时中心线速度分布对比 (a)垂直速度; (b)水平速度
Figure 4. The comparisons of the velocity profiles along the centerlines at $ Re = 1000 $: (a) The vertical velocity profile; (b) the horizontal velocity profile.
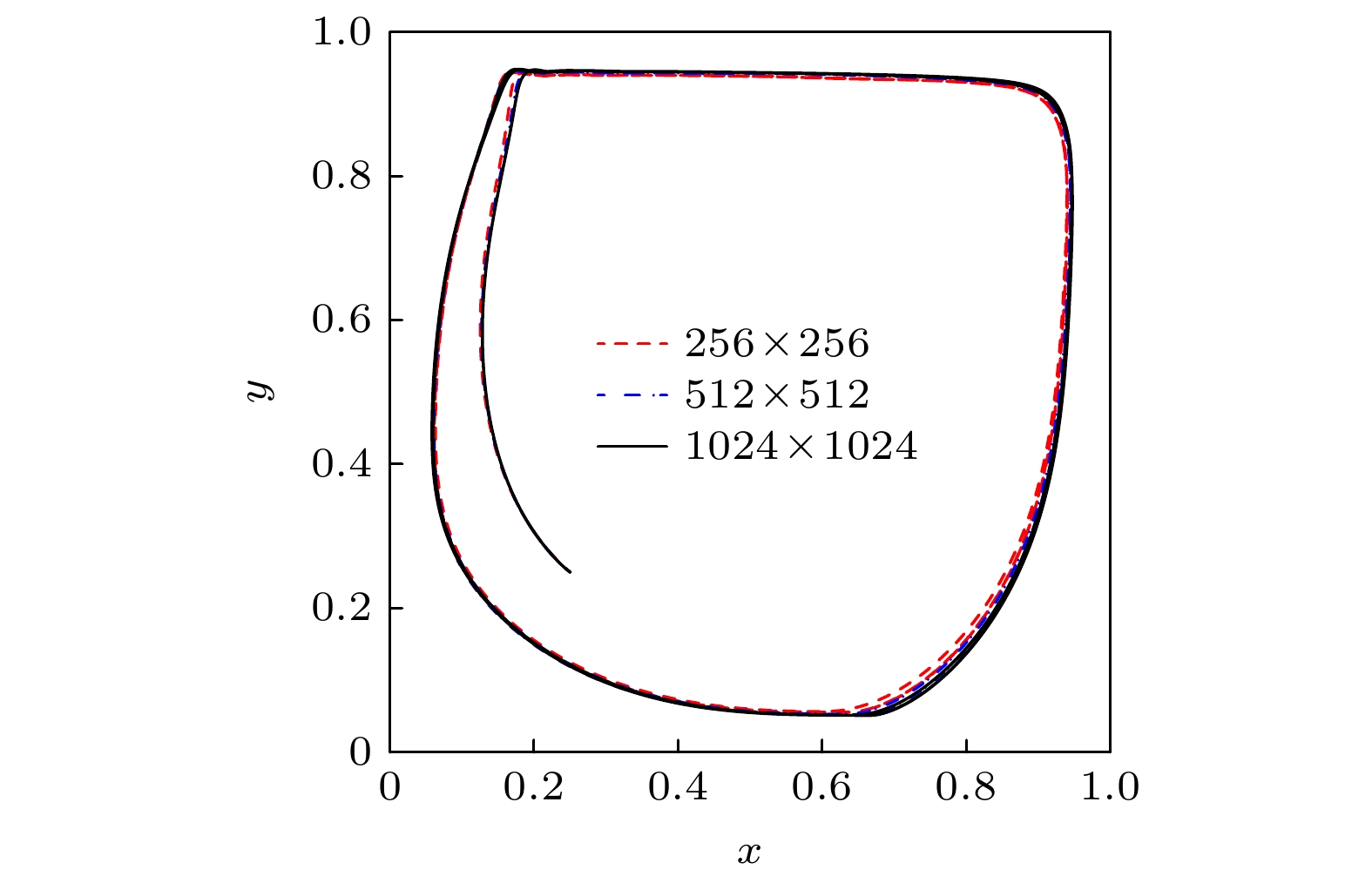
图 5 圆形颗粒在不同网格尺寸顶盖驱动流中的运动轨迹($ N_{x}\times N_{y} = 256\times 256 $, $ 512\times 512 $, $ 1024\times 1024 $)
Figure 5. The trajectories of a circular particle moving in a lid-driven cavity with three different grid sizes ($ N_{x}\times $$ N_{y} = 256\times 256 $, $ 512\times 512 $, $ 1024\times 1024 $).
图 6 圆形颗粒在幂律流体顶盖驱动流中的运动轨迹 (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $
Figure 6. The trajectories of the circular particle moving in the lid-driven cavity flows under different power-law indices and different initial positions: (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $n = 1.5 $.
图 7 圆形颗粒在幂律流体顶盖驱动流中运动的极限环 (a) $ Re = 500 $; (b) $ Re = 1000 $; (c) $ Re = 2000 $
Figure 7. The limit cycles of the circular particle moving in the power-law lid-driven cavity flows with different power-law indices and Reynolds numbers: (a) $ Re = 500 $; (b) $ Re = 1000 $; (c) $ Re = 2000 $.
图 8 幂律流体顶盖驱动流的流线及圆形颗粒的位置 (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $
Figure 8. The streamlines of power-law fluid flows and the positions of the circular particle under different power-law indices: (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $.
图 9 不同幂律指数($ n = 0.5 $, $ 1.0 $和$ 1.5 $)下圆形颗粒的速度 (a) $ Re = 500 $; (b) $Re = 1000 $; (c) $Re = 2000 $
Figure 9. The evolutions of particle velocity under different power-law indices: (a) $ Re = 500 $; (b) $ Re = 1000 $; (c) $Re = 2000 $.
图 10 不同颗粒尺寸和幂律指数下颗粒运动的极限环 (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $
Figure 10. The limit cycles of the moving particle in the power-law lid-driven cavity flows with different particle sizes and power-law indices: (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $.
图 11 不同颗粒尺寸和幂律指数下颗粒的运动速度 (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $
Figure 11. The evolutions of particle velocity under different particle sizes and power-law indices: (a) $ n = 0.5 $; (b) $ n = 1.0 $; (c) $ n = 1.5 $.
图 12 不同幂律指数下幂律流体顶盖驱动流(Re = 1000, r = 0.2)的圆形颗粒位置和流线 (a) n = 0.5; (b) n = 1.0; (c) n = 1.5
Figure 12. The positions of circular particle and the streamlines of the power-law lid-driven cavity flows (Re = 1000, r = 0.2) with different power-law indices: (a) n = 0.5; (b) n = 1.0; (c) n = 1.5.
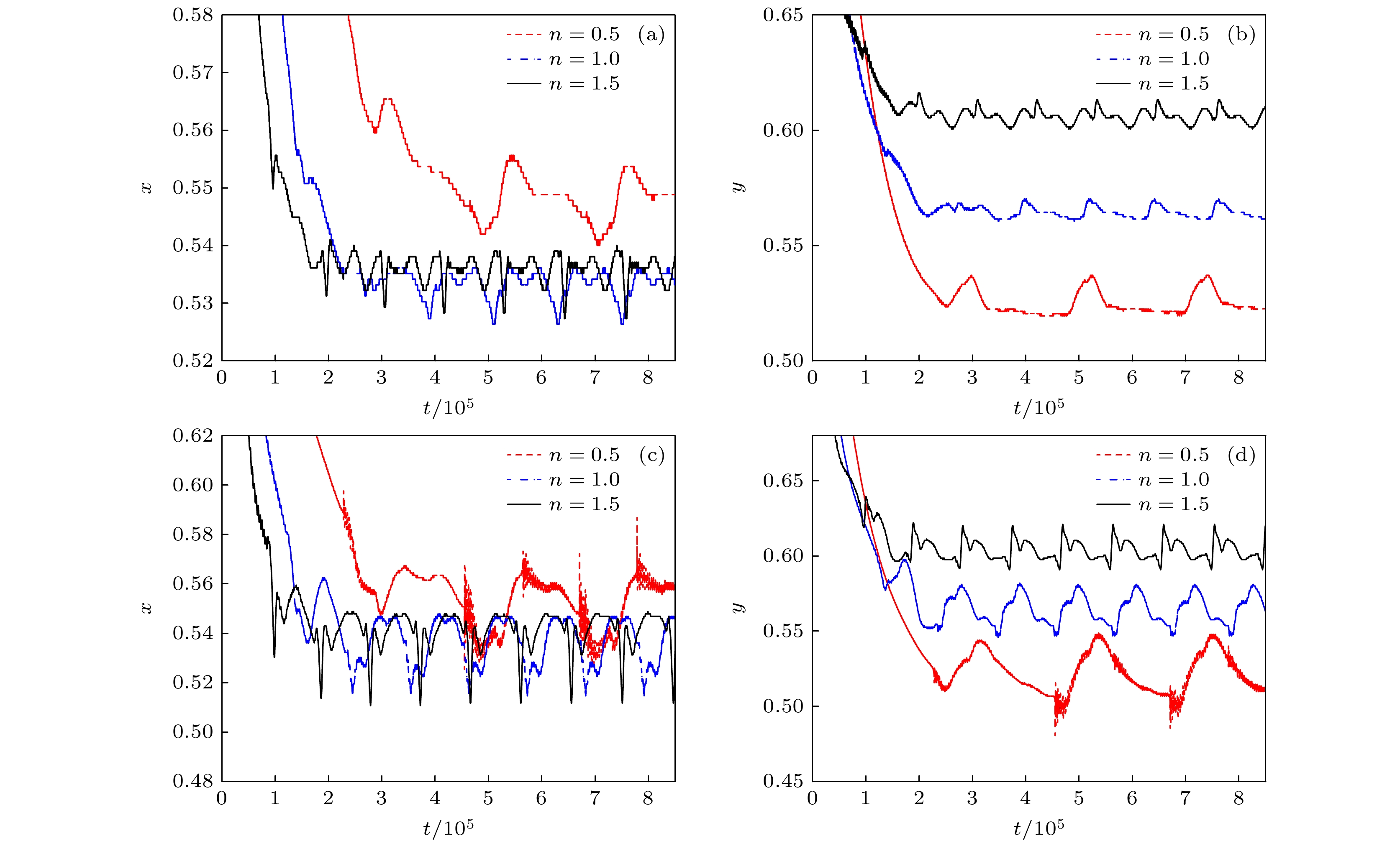
图 13 主涡涡心位置的水平、竖直坐标坐标随时间变化图 (a) $ x $轴坐标, $ r = 0.1 $; (b) $ y $轴坐标, $ r = 0.1 $; (c) $ x $轴坐标, $ r = 0.2 $; (d) $ y $轴坐标, $ r = 0.2 $
Figure 13. The evolutions of the x-axis and y-axis coordinates of position of primary vortex: (a) x-axis, $ r = 0.1 $; (b) y-axis, $ r = 0.1 $; (c) x-axis, $ r = 0.2 $; (d) y-axis, $ r = 0.2 $.
-
[1] Chhabra R P 2006 Bubbles, Drops, and Particles in Non-Newtonian Fluids (Boca Raton: CRC Press) pp40-74
[2] 朱克勤 2006 力学与实践 28 1
Google Scholar
Zhu K Q 2006 Mech. Eng. 28 1
Google Scholar
[3] Saramito P, Roquet N 2001 Comput. Methods Appl. Mech. Eng. 190 5391
Google Scholar
[4] Neofytou P 2005 Adv. Eng. Software 36 664
Google Scholar
[5] Rafiee A 2008 Anziam J. 49 411
Google Scholar
[6] Bell B C, Surana K S 1994 Int. J. Numer. Methods Fluids 18 127
Google Scholar
[7] Papanastasiou T C, Boudouvis A G 1997 Comput. Geotech. 64 677
[8] Papanastasiou T C 1987 J. Rheol. 31 385
Google Scholar
[9] Roquet N, Saramito P 2008 J. Non-Newtonian Fluid Mech. 155 101
Google Scholar
[10] Tazangi H R, Goharrizi A S, Javaran E J 2021 Korea-Aust. Rheol. J. 33 293
Google Scholar
[11] Schreiber R, Keller H B 1983 J. Comput. Phys. 49 310
Google Scholar
[12] Botella O, Peyret R 1998 Comput. Fluids 27 421
Google Scholar
[13] Erturk E, Corke T C 2005 Int. J. Numer. Methods Fluids 48 747
Google Scholar
[14] Mendu S S, Das P K 2012 J. Non-Newtonian Fluid Mech. 175–176 10
[15] Li Q X, Hong N, Shi B C, Chai Z H 2014 Commun. Comput. Phys. 15 265
Google Scholar
[16] Aguirre A, Castillo E, Cruchaga M, Codina R, Baiges J 2018 J. Non-Newton. Fluid Mech. 257 22
Google Scholar
[17] Alleborn N, Raszillier H, Durst F 1999 Int. J. Heat Mass Trans. 42 833
Google Scholar
[18] Stephen T, Nathan E 2007 Geology 35 1027
[19] Zhong H C, Zhou J, Du Z X, Xie L 2018 J. Aerosol Sci. 121 31
Google Scholar
[20] Madankan R, Pouget S, Singla P, Bursik M, Dehn J, Jones M, Patra A, Pavolonis M, Pitman E B, Singh T, Webley P 2014 J. Comput. Phys. 271 39
Google Scholar
[21] Yue G X, Cai R X, Lu J F, Zhang H 2017 Powder Technol. 316 18
Google Scholar
[22] He W C, Lv X W, Pan F F, Li X Q, Yan Z M 2019 Powder Technol. 356 1087
Google Scholar
[23] Sidik N A C, Attarzadeh S M R 2011 Int. J. Mech. 5 123
[24] Romanò F, Kuhlmann H C 2017 Theor. Comput. Fluid Dyn. 31 427
Google Scholar
[25] Hu J J, Sun D K, Mao S H, Wu H M, Yu S Y, Xu M S 2022 J. Comput. Theor. Transp. 51 222
Google Scholar
[26] Hu J J 2021 Int. J. Mod. Phys. C 32 1
[27] Hu J J 2020 Phys. Fluids 32 222
[28] Safdari A, Kim K C 2014 Comput. Math. Appl. 68 606
Google Scholar
[29] Francescò R, Hendrik H C 2017 Theor. Comput. Fluid Dyn. 31 1
[30] Chen S, Doolen G D 1998 Rev. Fluid Mech. 30 329
Google Scholar
[31] Succi S 2001 The Lattice Boltzmann Equation for Fluid Dynamics and Beyond (Oxford: Oxford University Press) pp3-38
[32] Guo Z L, Shu C 2013 Lattice Boltzmann Method and Its Applications in Engineering (Singapore: World Scientific Publishing Co.) pp10-21
[33] Krüger T, Kusumaatmaja H, Silva G, Shardt O, Kuzmin A, Viggen E M 2017 The Lattice Boltzmann Method: Principles and Practice (Switzerland: Springer International Publishing) pp61-65
[34] Feng J, Hu H H, Joseph D D 1994 J. Fluid Mech. 277 271
Google Scholar
[35] Inamuro T, Maeba K, Ogino F 2000 Int. J. Multiphase. Flow 26 1981
Google Scholar
[36] Shao X, Yu Z, Sun B 2008 Phys. Fluids 20 103307
Google Scholar
[37] Noble D R, Torczynski J R 1998 Int. J. Modern Phys. C 9 1189
Google Scholar
[38] Liu J, Huang C S, Chai Z H, Shi B C 2022 Comput. Fluids 233 105240
Google Scholar
[39] Liu J, Chai Z H, Shi B C 2022 Phys. Rev. E 106 015306
Google Scholar
[40] Boyd J, Buick J, Green S 2006 J. Phys. A 39 14241
Google Scholar
[41] Tang G H, Li X F, He Y L, Tao W Q 2009 J. Non-Newton. Fluid Mech. 157 133
Google Scholar
[42] Chai Z H, Shi B C, Guo Z L, Rong F M 2011 J. Non-Newton. Fluid Mech. 166 332
Google Scholar
[43] Guo Z L, Zheng C G, Shi B C 2002 Chin. Phys. 11 366
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1359
- PDF Downloads: 46
- Cited By: 0
