-
Mesoscopic methods serve as a pivotal link between the macroscopic and microscopic scales, offering a potent solution to the challenge of balancing physical accuracy with computational efficiency. Over the past decade, significant progress has been made in the application of the discrete Boltzmann method (DBM), which is a mesoscopic method based on a fundamental equation of nonequilibrium statistical physics (i.e., the Boltzmann equation), in the field of nonequilibrium fluid systems. The DBM has gradually become an important tool for describing and predicting the behavior of complex fluid systems. The governing equations comprise a set of straightforward and unified discrete Boltzmann equations, and the choice of their discrete format significantly influences the computational accuracy and stability of numerical simulations. In a bid to bolster the reliability of these simulations, this paper utilizes the finite volume method as a solution for handling the discrete Boltzmann equations. The finite volume method stands out as a widely employed numerical computation technique, known for its robust conservation properties and high level of accuracy. It excels notably in tackling numerical computations associated with high-speed compressible fluids. For the finite volume method, the value of each control volume corresponds to a specific physical quantity, which makes the physical connotation clear and the derivation process intuitive. Moreover, through the adoption of suitable numerical formats, the finite volume method can effectively minimize numerical oscillations and exhibit strong numerical stability, thus ensuring the reliability of computational results. Particularly, the MUSCL format where a flux limiter is introduced to improve the numerical robustness is adopted for the reconstruction in this paper. Ultimately, the DBM utilizing the finite volume method is rigorously validated to assess its proficiency in addressing flow issues characterized by pronounced discontinuities. The numerical experiments encompass scenarios involving shock waves, Lax shock tubes, and acoustic waves. The results demonstrate the method's precise depiction of shock wave evolution, rarefaction waves, acoustic phenomena, and material interfaces. Furthermore, it ensures the conservation of mass, momentum, and energy within the system, as well as accurately measures the hydrodynamic and thermodynamic nonequilibrium effects of the fluid system. Compared with the finite difference method, the finite volume method is also more convenient and flexible in dealing with boundary conditions of different geometries, and can be adapted to a variety of systems with complex boundary conditions. Consequently, the finite volume method further broadens the scope of DBM in practical applications.
-
Keywords:
- discrete Boltzmann method /
- finite volume method /
- nonequilibrium effect /
- compressible flow
[1] 阎超 2006 计算流体力学方法及应用 (北京: 北京航空航天大学出版社) 第1—14页
Yan C 2006 Computational Fluid Dynamics Methods and Applications (Beijing: Beihang University Press) pp1–14
[2] Xu A G, Zhang G C, Gan Y B, Chen F, Yu X J 2012 Front. Phys. 7 582
Google Scholar
[3] Leach A R 2001 Molecular Modelling: Principles and Applications (London: Pearson education) pp7-53
[4] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第1—12页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) pp1–12
[5] 何雅玲, 王勇, 李庆 2009 格子Boltzmann方法的理论及应用 (北京: 科学出版社) 第1—7页
He Y L, Wang Y, Li Q 2009 Lattice Boltzmann Method: Theory and Applicatuons (Beijing: Science Press) pp1–7
[6] 张涵信, 沈孟育 2003 计算流体力学: 差分方法的原理和应用 (北京: 国防工业出版社) 第1—230页
Zhang H X, Shen M Y 2003 Compatutional Fluid Dynamics: Fundamentals and Applications of Finite Difference Methods (Beijing: National Defense Industry Press) pp1–230
[7] Darwish M, Moukalled F 2016 The Finite Volume Method in Computational Fluid Dynamics: an Advanced Introduction with OpenFOAM and Matlab (Berlin: Springer) pp103–207
[8] 章本照, 印建安, 张宏基 2003 流体力学数值方法 (北京: 机械工业出版社) 第1—53页
Zhang B Z, Yin J A, Zhang H J 2003 Numerical Methods in Fluid Dynamics (Beijing: China Machine Press) pp1–53
[9] 许爱国, 张玉东 2022 复杂介质动理学 (北京: 科学出版社) 第1—112页
Xu A G, Zhang Y D 2022 Complex Media Kinetics (Beijing: Science Press) pp1–112
[10] Lin C D, Xu A G, Zhang G C, Li Y, Succi S 2014 Phys. Rev. E 89 013307
Google Scholar
[11] Zhang Y D, Xu A G, Zhang G C, Chen Z H, Wang P 2019 Comput. Phys. Commun. 238 50
Google Scholar
[12] Ji Y, Lin C D, Luo K H 2021 AIP Adv. 11 045217
Google Scholar
[13] 林传栋 2022 空气动力学学报 40 98
Google Scholar
Lin C D 2022 Acta Aerodyn. Sin. 40 98
Google Scholar
[14] Lin C D, Sun X P, Su X L, Lai H L, Fang X 2023 Chin. Phys. B 32 110503
Google Scholar
[15] Sun G L, Gan Y B, Xu A G, Shi Q F 2023 arXiv: 2311.06546 [physics.flu-dyn]
[16] Bhatnagar P L, Gross E P, Krook M 1954 Phys. Rev. 94 511
Google Scholar
[17] Lin C D, Luo K H 2019 Phys. Rev. E 99 012142
Google Scholar
[18] Van Leer B 1979 J. Comput. Phys. 32 101
Google Scholar
[19] Gottlieb S, Shu C W 1998 Math. Comput. 67 73
Google Scholar
[20] Lin C D, Luo K H, Xu A G, Gan Y B, Lai H L 2021 Phys. Rev. E 103 013305
Google Scholar
-
图 1 离散速度(a)与控制单元的示意图(b)
Figure 1. Sketches of discrete velocities (a) and control volumes (b).
图 2 网格无关性验证 (a)不同网格数下冲击波波阵面附近的压强分布; (b)不同空间步长下的相对误差
Figure 2. Grid-independence validation: (a) Pressure distribution in the vicinity of the shock wave for different grid numbers; (b) relative errors at different spatial steps.
图 3 冲击波周围的物理量, t = 0.375 (a) 密度; (b) 水平速度; (c) 温度; (d) 压强
Figure 3. Physical quantities around the shock wave, t = 0.375: (a) Density; (b) horizontal velocity; (c) temperature; (d) pressure.
图 4 冲击波周围的非平衡量, t =0.375
Figure 4. Nonequilibrium quantities around the shock wave, t =0.375.
图 5 Lax激波管中的物理量, t = 0.15 (a) 密度; (b) 水平速度; (c) 温度; (d) 压强
Figure 5. Physical quantities in the Lax shock tube, t = 0.15: (a) Density; (b) horizontal velocity; (c) temperature; (d) pressure.
图 6 在声波传播过程中不同时刻的压强分布图, $\gamma = 1.4,\;T=1.0 $, t = 0, 0.050, 0.125, 0.150, 0.175和0.200
Figure 6. Pressure contours in the evolution of a sound wave at time instants t = 0, 0.050, 0.125, 0.150, 0.175, and 0.200, respectively, $\gamma = 1.4,\;T=1.0 $.
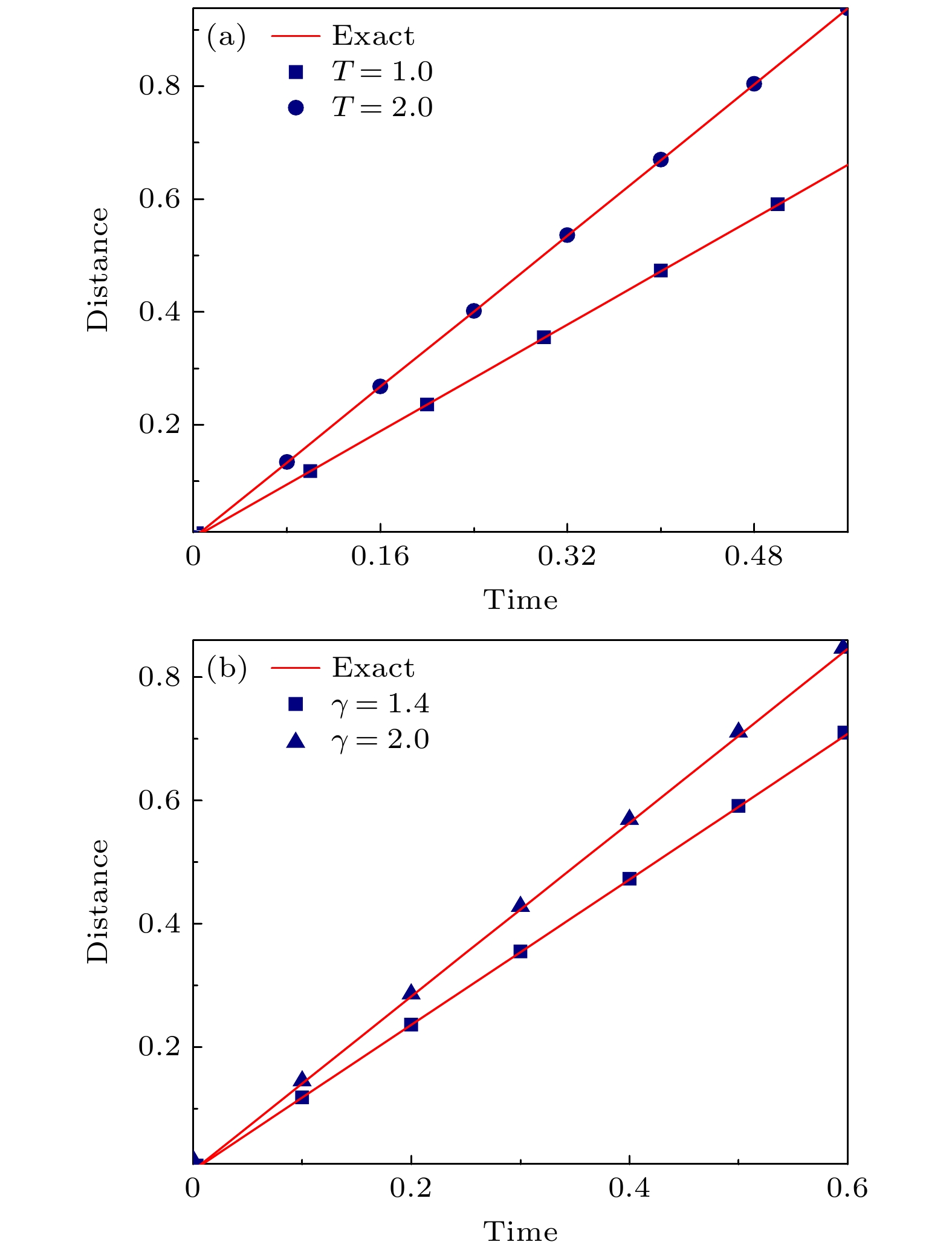
图 7 质量、动量和能量的守恒性验证: 正方形、菱形、三角形和圆形分别表示平均密度、x方向平均动量、y方向平均动量和平均能量. 实线代表对应的精确解
Figure 7. Verification of the conservation of mass, momentum and energy. Squares, diamonds, triangles and circles represent the average values of density, momentum in the x direction, momentum in the y direction and energy, respectively. The solid lines denotes the corresponding exact solutions.
图 8 声波的传播 (a)$\gamma = 1.4 $, 不同温度; (b)$ T = 1.0 $, 不同比热比
Figure 8. Propagation of the sound wave: (a) $ \gamma = 1.4 $ with various specific heat ratios; (b) $ T = 1.0 $ with various temperatures.
-
[1] 阎超 2006 计算流体力学方法及应用 (北京: 北京航空航天大学出版社) 第1—14页
Yan C 2006 Computational Fluid Dynamics Methods and Applications (Beijing: Beihang University Press) pp1–14
[2] Xu A G, Zhang G C, Gan Y B, Chen F, Yu X J 2012 Front. Phys. 7 582
Google Scholar
[3] Leach A R 2001 Molecular Modelling: Principles and Applications (London: Pearson education) pp7-53
[4] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第1—12页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) pp1–12
[5] 何雅玲, 王勇, 李庆 2009 格子Boltzmann方法的理论及应用 (北京: 科学出版社) 第1—7页
He Y L, Wang Y, Li Q 2009 Lattice Boltzmann Method: Theory and Applicatuons (Beijing: Science Press) pp1–7
[6] 张涵信, 沈孟育 2003 计算流体力学: 差分方法的原理和应用 (北京: 国防工业出版社) 第1—230页
Zhang H X, Shen M Y 2003 Compatutional Fluid Dynamics: Fundamentals and Applications of Finite Difference Methods (Beijing: National Defense Industry Press) pp1–230
[7] Darwish M, Moukalled F 2016 The Finite Volume Method in Computational Fluid Dynamics: an Advanced Introduction with OpenFOAM and Matlab (Berlin: Springer) pp103–207
[8] 章本照, 印建安, 张宏基 2003 流体力学数值方法 (北京: 机械工业出版社) 第1—53页
Zhang B Z, Yin J A, Zhang H J 2003 Numerical Methods in Fluid Dynamics (Beijing: China Machine Press) pp1–53
[9] 许爱国, 张玉东 2022 复杂介质动理学 (北京: 科学出版社) 第1—112页
Xu A G, Zhang Y D 2022 Complex Media Kinetics (Beijing: Science Press) pp1–112
[10] Lin C D, Xu A G, Zhang G C, Li Y, Succi S 2014 Phys. Rev. E 89 013307
Google Scholar
[11] Zhang Y D, Xu A G, Zhang G C, Chen Z H, Wang P 2019 Comput. Phys. Commun. 238 50
Google Scholar
[12] Ji Y, Lin C D, Luo K H 2021 AIP Adv. 11 045217
Google Scholar
[13] 林传栋 2022 空气动力学学报 40 98
Google Scholar
Lin C D 2022 Acta Aerodyn. Sin. 40 98
Google Scholar
[14] Lin C D, Sun X P, Su X L, Lai H L, Fang X 2023 Chin. Phys. B 32 110503
Google Scholar
[15] Sun G L, Gan Y B, Xu A G, Shi Q F 2023 arXiv: 2311.06546 [physics.flu-dyn]
[16] Bhatnagar P L, Gross E P, Krook M 1954 Phys. Rev. 94 511
Google Scholar
[17] Lin C D, Luo K H 2019 Phys. Rev. E 99 012142
Google Scholar
[18] Van Leer B 1979 J. Comput. Phys. 32 101
Google Scholar
[19] Gottlieb S, Shu C W 1998 Math. Comput. 67 73
Google Scholar
[20] Lin C D, Luo K H, Xu A G, Gan Y B, Lai H L 2021 Phys. Rev. E 103 013305
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2152
- PDF Downloads: 119
- Cited By: 0
