Simulation study of drag force characteristics of nanoparticles in transition regime

Liu Wang-Wang; Zhang Ke-Xue; Wang Jun; Xia Guo-Dong

doi:10.7498/aps.73.20231861

Abstract

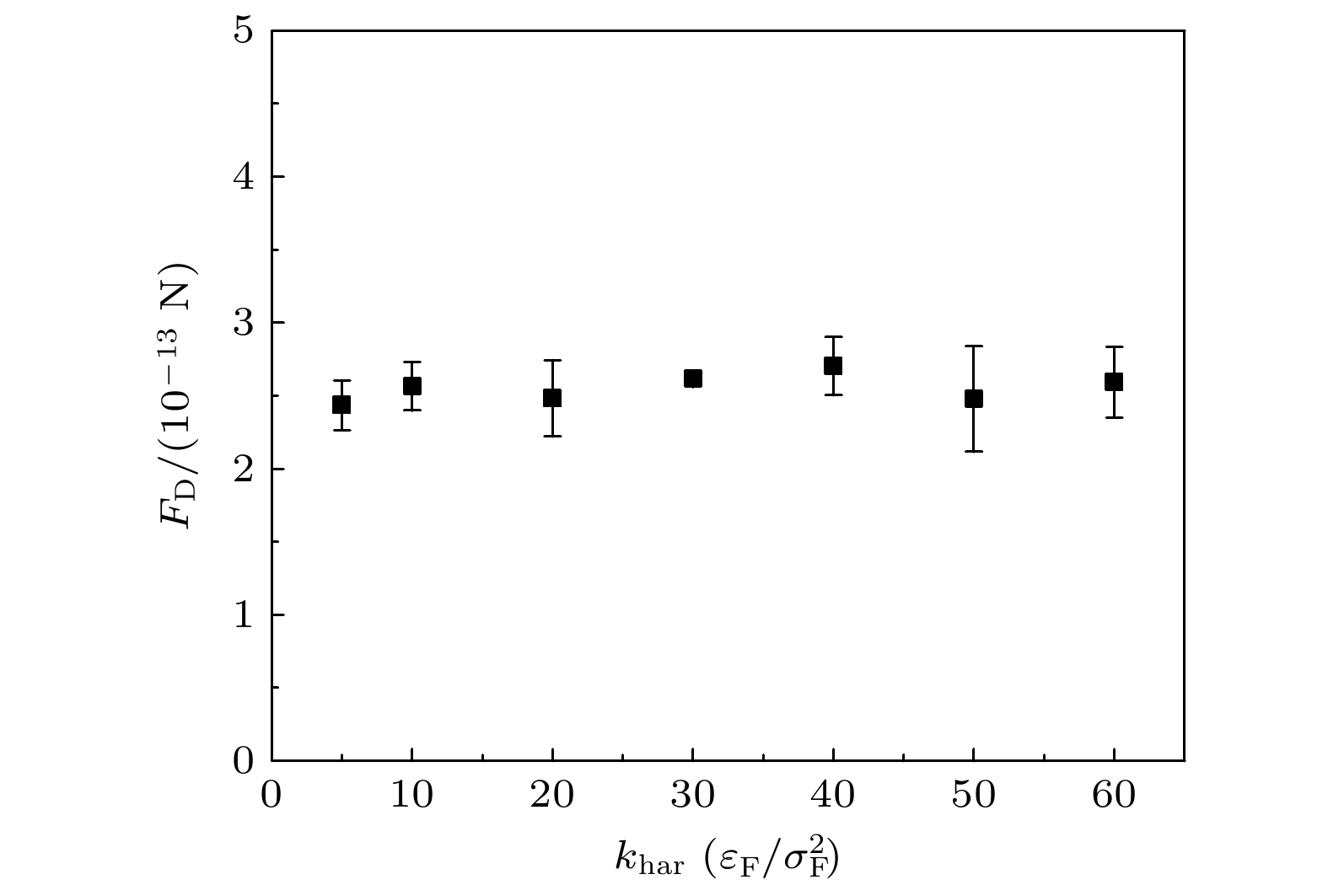
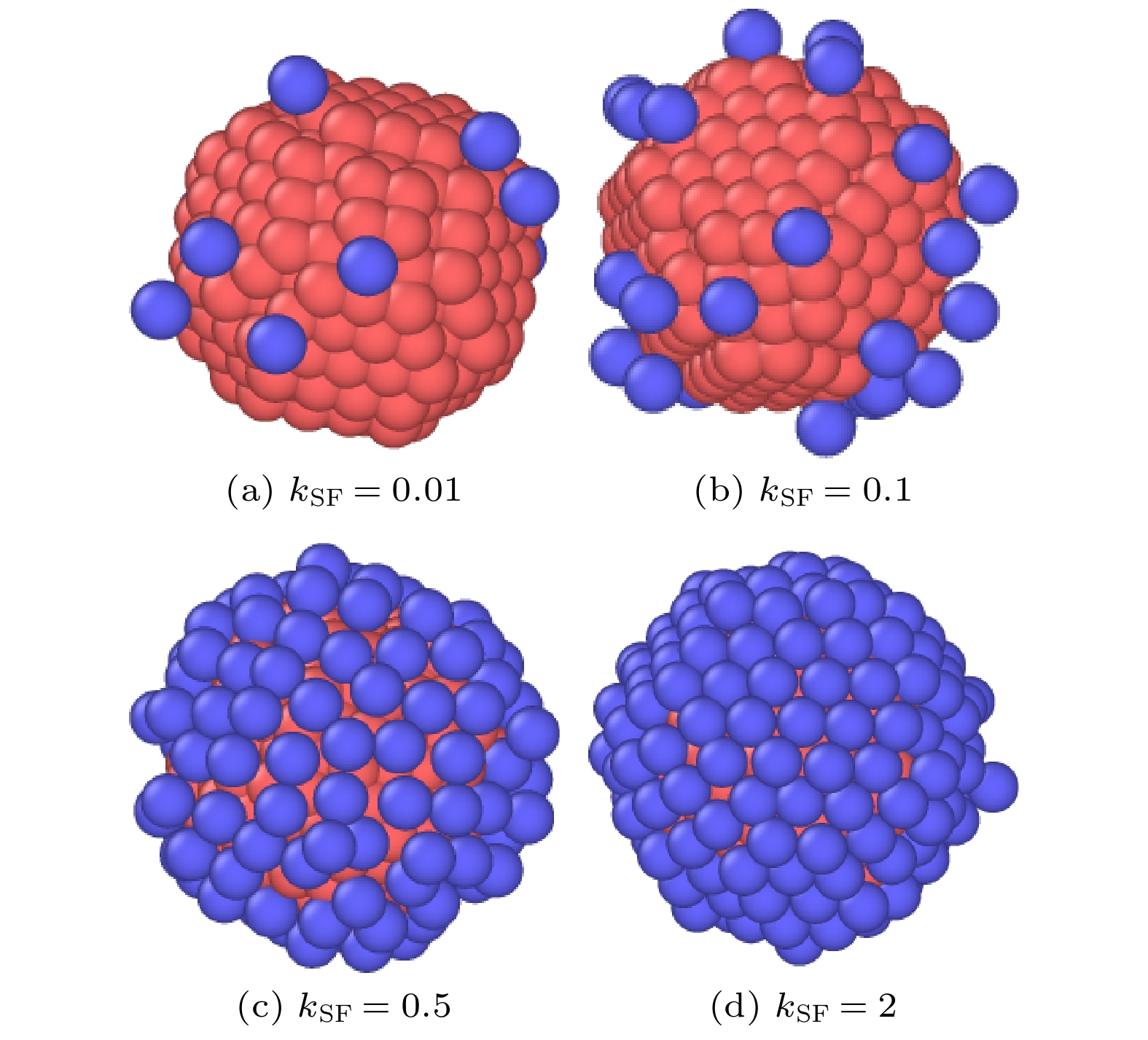
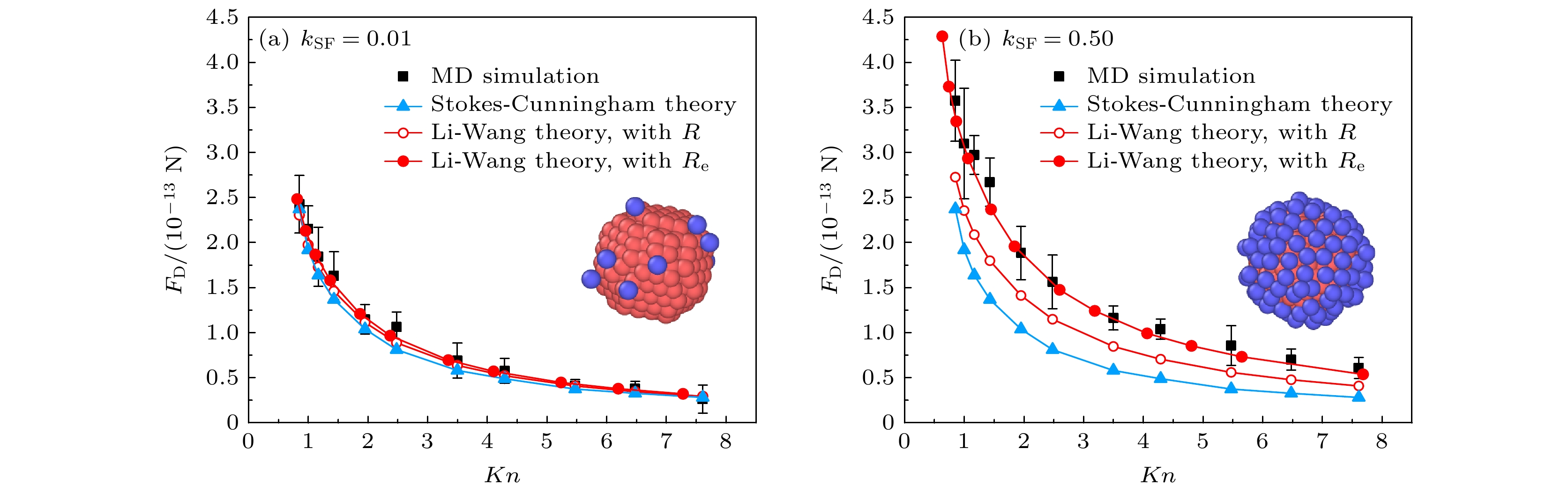
Transport properties of nanoparticles in gases have many practical applications, such as aerosol science, combustion, and micro- and nano-scale fabrication. A nanoparticle moving in a fluid is expected to experience a drag force, which determines the transport property of the particle. According to the Einstein relationship, the diffusion coefficient of a particle is inversely proportional to the drag force coefficient. However, in the transition regime, it is usually difficult to evaluate the drag force of suspended particles. A typical method is to extend the asymptotic solution of the free molecular or continuum limit to the transition regime. According to the gas kinetic theory, Li and Wang proposed a theoretical expression for drag force on nanoparticles in the free molecular regime, which is then extended to the entire range of Knudsen number following a semi-empirical approach [Li Z G, Wang H 2003 Phys. Rev. E 68 061207]. For nanoparticles, it is necessary to verify the theoretical predictions since the gas-particle non-rigid-body interactions must be taken into account. In this work, the drag force on nanoparticle in the transition regime is investigated by using molecular dynamics (MD) simulation. To evaluate the drag force, a harmonic potential is used to the nanoparticle to constrain its Brownian motion in our MD simulation. In the steady state, the drag force can be obtained by the balance between the drag force and harmonic force. It is found that the gas-particle non-rigid-body interaction has a significant influence on the drag force of nanoparticle. For weak gas-solid coupling, the MD simulation results can be in good agreement with the prediction of Li-Wang theory. However, for strong coupling, there exists significant discrepancy between the MD simulation results and the theoretical results. Due to the gas-solid intermolecular interactions, gas molecules can be adsorbed on the nanoparticle surface, and after a time period, they may be re-emitted from the surface when they gain sufficient kinetic energy. Therefore, an adsorption-desorption equilibrium and an adsorption layer can be established on the particle surface. The adsorption layer enlarges the collision cross-sectional area and enhances the momentum transfer between gas molecules and the particle, and thus the drag force increases. This can explain the inconsistencies between the theoretical results and MD simulations. In this work, we introduce an adsorption ratio to evaluate the thickness of the adsorption layer. Then, the effective particle radius can be defined by the sum of particle radius and the thickness of the adsorption layer. By using the effective particle radius, the simulation values are in very good agreement with the theoretical predictions. The results of this work provide insights into the applications of nanoparticles in aerosol science.

Keywords:

Authors and contacts

Beijing Key Laboratory of Heat Transfer and Energy Conversion, MOE Key Laboratory of Enhanced Heat Transfer and Energy Conservation, Beijing University of Technology, Beijing 100124, China

Corresponding author: Wang Jun, jwang@bjut.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 51776007).

FullText HTML : translate this paragraph

References

[1]	Li Z G 2009 Phys. Rev. E 80 061204 Google Scholar
[2]	Wong R Y M, Liu C R, Wang J, Chao C Y H, Li Z G 2012 J. Nanosci. Nanotechnol. 12 2311 Google Scholar
[3]	Livi C, Staso G D, Clercx H J H, Toschi F 2022 Phys. Rev. E 105 015306 Google Scholar
[4]	Qiu J, Qiu T T 2015 Carbon 81 20 Google Scholar
[5]	Zhang Y Y, Li S Q, Yan W, Yao Q 2012 Powder Technol. 227 24 Google Scholar
[6]	Breddan M J D, Wirz R E 2023 J. Aerosol Sci. 167 106079 Google Scholar
[7]	Westmeiera D, Solouk-Saranb D, Vallet C 2018 Proc. Natl. Acad. Sci. 115 7087 Google Scholar
[8]	Pankhurst Q, Jones S, Dobson J 2016 J. Phys. D: Appl. Phys. 49 501002 Google Scholar
[9]	Mackus A J M, Weber M J, Thissen N F W, Garcia-Alonso D, Vervuurt R H J, Assali S, Bol A A, Verheijen M A, Kessels W M M 2015 Nanotechnology 27 034001 Google Scholar
[10]	Linic S, Aslam U, Boerigter C, Morabito M 2015 Nat. Mater. 14 567 Google Scholar
[11]	Givehchi R, Tan Z 2015 J. Aerosol Sci. 83 12 Google Scholar
[12]	Liu C R, Li Z G, Wang H 2016 Phys. Rev. E 94 023102 Google Scholar
[13]	刘东静, 周福, 陈帅阳, 胡志亮 2023 72 157901 Google Scholar Liu D J, Zhou F, Chen S Y, Hu Z L 2023 Acta Phys. Sin. 72 157901 Google Scholar
[14]	Wang J, Su J J, Xia G D 2020 Phys. Rev. E 101 013103 Google Scholar
[15]	Gutiérrez-Varela O, Santamaria R 2021 J. Mol. Liq. 338 116466 Google Scholar
[16]	郭瑞雪, 艾保全 2023 72 200501 Google Scholar Guo R X, Ai B Q 2023 Acta Phys. Sin. 72 200501 Google Scholar
[17]	Liao M J, Wei M T, Xu S X, Ouyang D H, Sheng P 2019 Chin. Phys. B 28 084701 Google Scholar
[18]	刘晨昊, 刘天宇, 黄仁忠, 高天附, 舒咬根 2019 68 240501 Google Scholar Liu C H, Liu T Y, Huang R Z, Gao T F, Shu Y G 2019 Acta Phys. Sin. 68 240501 Google Scholar
[19]	Epstein P S 1924 Phys. Rev. 23 710 Google Scholar
[20]	Stokes G G 1851 Proc. Cambridge Philos. Soc. 9 8
[21]	Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (Oxford: Clarendon Press) p55
[22]	Cunningham E 1910 Proc. R. Soc. London, Ser. A 83 357 Google Scholar
[23]	Allen M D, Raabe O G 1982 J. Aerosol Sci. 13 537 Google Scholar
[24]	Liu C R, Wang H 2019 Phys. Rev. E 99 042127 Google Scholar
[25]	Su J J, Wang J, Xia G D 2021 Chin. Phys. B 30 075101 Google Scholar
[26]	Liu W, Wang J, Xia G D, Li Z G 2023 Phys. Fluids 35 083316 Google Scholar
[27]	Luo S, Wang J, Xia G D, Li Z G 2016 J. Fluid Mech. 795 443 Google Scholar
[28]	Wang J, Yu S, Luo S, Xia G D, Zong L 2018 Phys. Fluids 30 063302 Google Scholar
[29]	Luo S, Wang J, Yu S, Xia G D, Li Z G 2018 J. Fluid Mech. 846 392 Google Scholar
[30]	Li Z G, Wang H 2003 Phys. Rev. E 68 061206 Google Scholar
[31]	Li Z G, Wang H 2003 Phys. Rev. E 68 061207 Google Scholar
[32]	Zhou X W, Johnson R A, Wadley H N G 2004 Phys. Rev. B 69 144113 Google Scholar
[33]	Kröger M 2004 Phys. Rep. 390 453 Google Scholar
[34]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[35]	Galliero G, Volz S 2008 J. Chem. Phys. 128 064505 Google Scholar
[36]	Liu W, Cui J, Wang J, Xia G D, Li Z G 2023 Phys. Fluids 35 032004 Google Scholar
[37]	崔杰, 苏俊杰, 王军, 夏国栋, 李志刚 2021 70 055101 Google Scholar Cui J, Su J J, Wang J, Xia G D, Li Z G 2021 Acta Phys. Sin. 70 055101 Google Scholar
[38]	Tsuji T, Iseki H, Hanasaki I, Kawano S 2016 30th International Symposium on Rarefied Gas Dynamics 1786 110003 Google Scholar
[39]	Hess B 2002 J. Chem. Phys. 116 209 Google Scholar
[40]	Gomez A, Rosner D E 1993 Combust. Sci. Technol. 89 335 Google Scholar
[41]	马奥杰, 陈颂佳, 李玉秀, 陈颖 2021 70 148201 Google Scholar Ma A J, Chen S J, Li Y X, Chen Y 2021 Acta Phys. Sin. 70 148201 Google Scholar
[42]	Li Z G, Wang H 2005 Phys. Rev. Lett. 95 014502 Google Scholar
[43]	Liu C R, Li Z G 2010 Phys. Rev. Lett. 105 174501 Google Scholar
[44]	Li Z G 2009 Phys. Rev. E 79 026312 Google Scholar

Cited By

图 1 分子动力学模拟系统模型图(红色: 纳米颗粒; 蓝色: 气体分子)

Figure 1. Configuration of MD simulation system (Red: nanoparticle; blue: gas molecules).

DownLoad: Full-Size Img PowerPoint

图 2 纳米颗粒的曳力随弹性系数k_har的变化

Figure 2. Drag force on nanoparticles versus elastic coefficient k_har.

DownLoad: Full-Size Img PowerPoint

图 3 MD模拟值与理论公式在3种气固结合强度下的对比结果　(a) k_SF = 0.01; (b) k_SF = 0.1; (c) k_SF = 0.5

Figure 3. Comparison of MD simulation results of the drag force with theoretical values at various k_SF: (a) k_SF = 0.01; (b) k_SF = 0.1; (c) k_SF = 0.5.

DownLoad: Full-Size Img PowerPoint

图 4 气体分子在纳米颗粒表面吸附状况的模拟快照

Figure 4. Snapshots of the adsorption of gas molecules (blue) on the nanoparticle (red) surface.

DownLoad: Full-Size Img PowerPoint

图 5 吸附率α随气固结合强度k_SF的变化

Figure 5. Adsorption ratio α versus gas-particle coupling parameters k_SF.

DownLoad: Full-Size Img PowerPoint

图 6 MD模拟值与(2)式在3种气固结合强度下的对比结果

Figure 6. Comparison of MD simulation results of the drag force with Eq. (2) at various k_SF.

DownLoad: Full-Size Img PowerPoint

图 7 MD模拟值与(2)式在三种气固结合强度下的对比结果

Figure 7. Comparison of MD simulation results of the drag force with Eq. (2) at various k_SF.

DownLoad: Full-Size Img PowerPoint

DownLoad: Full-Size Img PowerPoint

表 1 LJ势函数参数值^[33]

Table 1. LJ potential parameters^[33].

σ/Å ε/K

Ar-Ar 3.405 114

Cu-Cu 2.338 4753

Cu-Ar 2.871 736

DownLoad: CSV

map

[1]	Li Z G 2009 Phys. Rev. E 80 061204 Google Scholar
[2]	Wong R Y M, Liu C R, Wang J, Chao C Y H, Li Z G 2012 J. Nanosci. Nanotechnol. 12 2311 Google Scholar
[3]	Livi C, Staso G D, Clercx H J H, Toschi F 2022 Phys. Rev. E 105 015306 Google Scholar
[4]	Qiu J, Qiu T T 2015 Carbon 81 20 Google Scholar
[5]	Zhang Y Y, Li S Q, Yan W, Yao Q 2012 Powder Technol. 227 24 Google Scholar
[6]	Breddan M J D, Wirz R E 2023 J. Aerosol Sci. 167 106079 Google Scholar
[7]	Westmeiera D, Solouk-Saranb D, Vallet C 2018 Proc. Natl. Acad. Sci. 115 7087 Google Scholar
[8]	Pankhurst Q, Jones S, Dobson J 2016 J. Phys. D: Appl. Phys. 49 501002 Google Scholar
[9]	Mackus A J M, Weber M J, Thissen N F W, Garcia-Alonso D, Vervuurt R H J, Assali S, Bol A A, Verheijen M A, Kessels W M M 2015 Nanotechnology 27 034001 Google Scholar
[10]	Linic S, Aslam U, Boerigter C, Morabito M 2015 Nat. Mater. 14 567 Google Scholar
[11]	Givehchi R, Tan Z 2015 J. Aerosol Sci. 83 12 Google Scholar
[12]	Liu C R, Li Z G, Wang H 2016 Phys. Rev. E 94 023102 Google Scholar
[13]	刘东静, 周福, 陈帅阳, 胡志亮 2023 72 157901 Google Scholar Liu D J, Zhou F, Chen S Y, Hu Z L 2023 Acta Phys. Sin. 72 157901 Google Scholar
[14]	Wang J, Su J J, Xia G D 2020 Phys. Rev. E 101 013103 Google Scholar
[15]	Gutiérrez-Varela O, Santamaria R 2021 J. Mol. Liq. 338 116466 Google Scholar
[16]	郭瑞雪, 艾保全 2023 72 200501 Google Scholar Guo R X, Ai B Q 2023 Acta Phys. Sin. 72 200501 Google Scholar
[17]	Liao M J, Wei M T, Xu S X, Ouyang D H, Sheng P 2019 Chin. Phys. B 28 084701 Google Scholar
[18]	刘晨昊, 刘天宇, 黄仁忠, 高天附, 舒咬根 2019 68 240501 Google Scholar Liu C H, Liu T Y, Huang R Z, Gao T F, Shu Y G 2019 Acta Phys. Sin. 68 240501 Google Scholar
[19]	Epstein P S 1924 Phys. Rev. 23 710 Google Scholar
[20]	Stokes G G 1851 Proc. Cambridge Philos. Soc. 9 8
[21]	Bird G A 1994 Molecular Gas Dynamics and the Direct Simulation of Gas Flows (Oxford: Clarendon Press) p55
[22]	Cunningham E 1910 Proc. R. Soc. London, Ser. A 83 357 Google Scholar
[23]	Allen M D, Raabe O G 1982 J. Aerosol Sci. 13 537 Google Scholar
[24]	Liu C R, Wang H 2019 Phys. Rev. E 99 042127 Google Scholar
[25]	Su J J, Wang J, Xia G D 2021 Chin. Phys. B 30 075101 Google Scholar
[26]	Liu W, Wang J, Xia G D, Li Z G 2023 Phys. Fluids 35 083316 Google Scholar
[27]	Luo S, Wang J, Xia G D, Li Z G 2016 J. Fluid Mech. 795 443 Google Scholar
[28]	Wang J, Yu S, Luo S, Xia G D, Zong L 2018 Phys. Fluids 30 063302 Google Scholar
[29]	Luo S, Wang J, Yu S, Xia G D, Li Z G 2018 J. Fluid Mech. 846 392 Google Scholar
[30]	Li Z G, Wang H 2003 Phys. Rev. E 68 061206 Google Scholar
[31]	Li Z G, Wang H 2003 Phys. Rev. E 68 061207 Google Scholar
[32]	Zhou X W, Johnson R A, Wadley H N G 2004 Phys. Rev. B 69 144113 Google Scholar
[33]	Kröger M 2004 Phys. Rep. 390 453 Google Scholar
[34]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[35]	Galliero G, Volz S 2008 J. Chem. Phys. 128 064505 Google Scholar
[36]	Liu W, Cui J, Wang J, Xia G D, Li Z G 2023 Phys. Fluids 35 032004 Google Scholar
[37]	崔杰, 苏俊杰, 王军, 夏国栋, 李志刚 2021 70 055101 Google Scholar Cui J, Su J J, Wang J, Xia G D, Li Z G 2021 Acta Phys. Sin. 70 055101 Google Scholar
[38]	Tsuji T, Iseki H, Hanasaki I, Kawano S 2016 30th International Symposium on Rarefied Gas Dynamics 1786 110003 Google Scholar
[39]	Hess B 2002 J. Chem. Phys. 116 209 Google Scholar
[40]	Gomez A, Rosner D E 1993 Combust. Sci. Technol. 89 335 Google Scholar
[41]	马奥杰, 陈颂佳, 李玉秀, 陈颖 2021 70 148201 Google Scholar Ma A J, Chen S J, Li Y X, Chen Y 2021 Acta Phys. Sin. 70 148201 Google Scholar
[42]	Li Z G, Wang H 2005 Phys. Rev. Lett. 95 014502 Google Scholar
[43]	Liu C R, Li Z G 2010 Phys. Rev. Lett. 105 174501 Google Scholar
[44]	Li Z G 2009 Phys. Rev. E 79 026312 Google Scholar

[1]	Wei Guo-Cui, Tian Ze-An. Molecular dynamics simulation of rapid solidification of Cu₆₄Zr₃₆ nanodrops of different sizes. Acta Physica Sinica, 2021, 70(24): 246401. doi: 10.7498/aps.70.20211235
[2]	Pan Ling, Zhang Hao, Lin Guo-Bin. Molecular dynamics simulation on dynamic behaviors of nanodroplets impinging on solid surfaces decorated with nanopillars. Acta Physica Sinica, 2021, 70(13): 134704. doi: 10.7498/aps.70.20210094
[3]	Ma Ao-Jie, Chen Song-Jia, Li Yu-Xiu, Chen Ying. Molecular dynamics simulation of Brownian diffusion boundary condition for nanoparticles. Acta Physica Sinica, 2021, 70(14): 148201. doi: 10.7498/aps.70.20202240
[4]	Cui Jie, Su Jun-Jie, Wang Jun, Xia Guo-Dong, Li Zhi-Gang. Thermophoretic force on nanoparticles in free molecule regime. Acta Physica Sinica, 2021, 70(5): 055101. doi: 10.7498/aps.70.20201629
[5]	Liang Yi-Ran, Liang Qing. Molecular simulation of interaction between charged nanoparticles and phase-separated biomembranes containning charged lipids. Acta Physica Sinica, 2019, 68(2): 028701. doi: 10.7498/aps.68.20181891
[6]	Wang Zuo, Liu Yan, Zhang Jia-Zhong. Simulation of micro flow in the transition regime using effective-viscosity-based multi-relaxation-time lattice Boltzmann model. Acta Physica Sinica, 2016, 65(1): 014703. doi: 10.7498/aps.65.014703
[7]	Lin Jia-Qi, Li Xiao-Kang, Yang Wen-Long, Sun Hong-Guo, Xie Zhi-Bin, Xiu Han-jiang, Lei Qing-Quan. Molecular dynamics simulation study on the structure and mechanical properties of polyimide/KTa0.5Nb0.5O3 nanoparticle composites. Acta Physica Sinica, 2015, 64(12): 126202. doi: 10.7498/aps.64.126202
[8]	Si Li-Na, Wang Xiao-Li. A molecular dynamics study on adhesive contact processes of surfaces with nanogrooves. Acta Physica Sinica, 2014, 63(23): 234601. doi: 10.7498/aps.63.234601
[9]	Su Jin-Fang, Song Hai-Yang, An Min-Rong. Molecular dynamics simulation on mechanical properties of gold nanotubes. Acta Physica Sinica, 2013, 62(6): 063103. doi: 10.7498/aps.62.063103
[10]	Li Ming-Lin, Lin Fan, Chen Yue. Study on the mechanical properties of carbon nanocones using molecular dynamics simulation. Acta Physica Sinica, 2013, 62(1): 016102. doi: 10.7498/aps.62.016102
[11]	Chen Qing, Sun Min-Hua. Molecular dynamics simulation of isothermal crystallization dynamics in Cu nanocluster. Acta Physica Sinica, 2013, 62(3): 036101. doi: 10.7498/aps.62.036101
[12]	Li Lin, Wang Xuan, Sun Wei-Feng, Lei Qing-Quan. Molecular dynamics simulation of polyethylene/silver-nanoparticle composites. Acta Physica Sinica, 2013, 62(10): 106201. doi: 10.7498/aps.62.106201
[13]	Sun Wei-Feng, Wang Xuan. Molecular dynamics simulation study of polyimide/copper-nanoparticle composites. Acta Physica Sinica, 2013, 62(18): 186202. doi: 10.7498/aps.62.186202
[14]	Chen Qing, Wang Shu-Ying, Sun Min-Hua. Molecular dynamics simulation of isothermal crystallization dynamics in Cu nanocluster. Acta Physica Sinica, 2012, 61(14): 146101. doi: 10.7498/aps.61.146101
[15]	Xia Dong, Wang Xin-Qiang. Structures and melting behaviors of ultrathin platinum nanowires. Acta Physica Sinica, 2012, 61(13): 130510. doi: 10.7498/aps.61.130510
[16]	Li Rui, Hu Yuan-Zhong, Wang Hui. Molecular dynamics simulation on carbon nanotube bundles sandwitched between Si surfaces. Acta Physica Sinica, 2011, 60(1): 016106. doi: 10.7498/aps.60.016106
[17]	Xie Fang, Zhu Ya-Bo, Zhang Zhao-Hui, Zhang Lin. Molecular dynamics simulation of multi-wall carbon nanotube oscillators. Acta Physica Sinica, 2008, 57(9): 5833-5837. doi: 10.7498/aps.57.5833
[18]	Jin Nian-Qing, Teng Yu-Yong, Gu Bin, Zeng Xiang-Hua. Study of rare-gas atom injection into defective carbon nanotube by molecular dynamics simulation. Acta Physica Sinica, 2007, 56(3): 1494-1498. doi: 10.7498/aps.56.1494
[19]	Meng Li-Jun, Zhang Kai-Wang, Zhong Jian-Xin. Molecular dynamics simulation of formation of silicon nanoparticles on surfaces of carbon nanotubes. Acta Physica Sinica, 2007, 56(2): 1009-1013. doi: 10.7498/aps.56.1009
[20]	Li Rui, Hu Yuan-Zhong, Wang Hui, Zhang Yu-Jun. Molecular dynamics simulation of motion of single-walled carbon nanotubes on graphite substrate. Acta Physica Sinica, 2006, 55(10): 5455-5459. doi: 10.7498/aps.55.5455

Catalog

Vol. 73, Issue 7 - 2024-04-05

Metrics

Abstract views: 1763
PDF Downloads: 83
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板