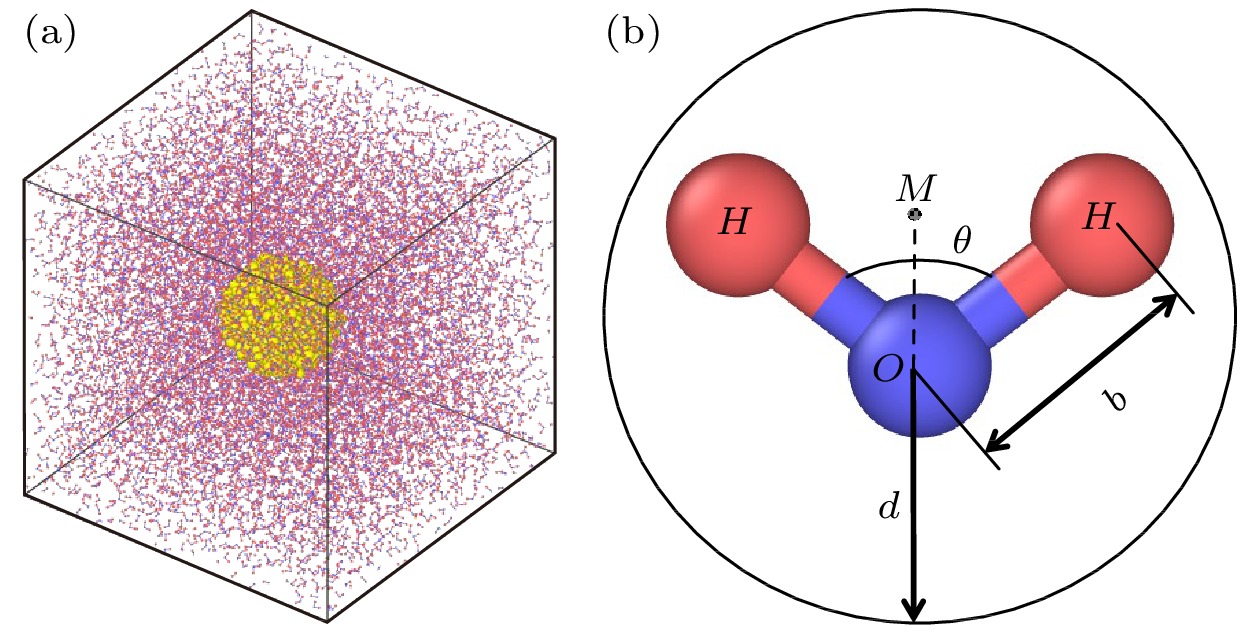
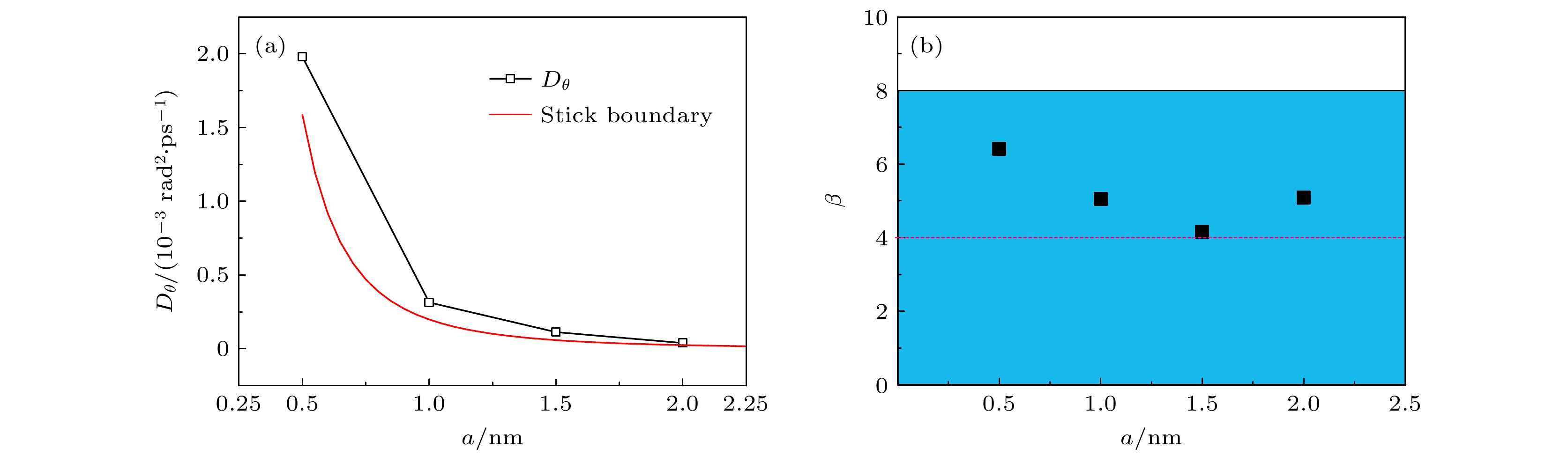
-
Brownian motion refers to the endless random motion of nanometer-to-micron particles suspended in a fluid. It widely exists in nature, and is applied to energy, biology, chemical industry, environment and other industries. As the Brownian motion of the object decreases from the micron level to the nanometer level, the boundary conditions of the particle motion no longer strictly follow the stick hydrodynamic boundary conditions, but are closer to the slip boundary theory, meanwhile, the interaction between particles and solvents has increasingly important influence on particle dynamics. Molecular dynamics simulation is an important means to study nanofluids, which can not only capture the microscopic details of the interactions between particles and solvent molecules in nanofluids, but also have high potential function accuracy. In this paper, an all-atom model of the diffusion of Cu nanoparticles of different sizes in water is established by using the rigid TIP4P/2005 water molecule model as solvent, the dynamic viscosity from the TIP4P/2005 model is in good agreement with the experimental result, which is verified by the Green-Kubo formula. The FCC lattice structure is used to construct Cu particles of 0.5 nm, 1.0 nm, 1.5 nm, 2.0 nm in size, and the interaction between atoms in the particle is described by the EAM potential. The translational diffusion coefficient of particles is fitted by the single particle tracking algorithm and the least square method, the rotational diffusion coefficient of particles is obtained by quaternion transformation. The diffusion coefficient and friction factor of the particles are calculated, and the friction factor is compared with the result under the stick hydrodynamics boundary conditions and the result under the slip boundary conditions. It is found that the frictional factors of translation and rotation of nano-particles lie between the theoretical values predicted by the two boundary conditions. The radial distribution functions of water molecules around nanoparticles of different sizes are calculated, we find that the smaller the particle size, the more obvious the adsorption of solvent molecules will be, and the water molecular layer on the particle surface will increase the effective volume of particles and make the calculation result of friction factor larger. The effect of solvent adsorption on the effective hydrodynamic radius of particles cannot be ignored when calculating the friction coefficient of Brownian motion of nano-particles, especially when the particle radius is close to the solvent radius. In Brownian dynamics, viscous resistance and stochastic force are constrained by fluctuation dissipation theorem, and a reasonable selection of particle friction factor can provide theoretical basis for the improvement of Brownian dynamics.
-
Keywords:
- nanoparticles /
- diffusion coefficient /
- friction factor /
- hydrodynamic radius
[1] Brown R 1828 Philos. Mag. 4 161
Google Scholar
[2] Einstein A 1905 Ann. Phys. 17 549
[3] Bian X, Kim C, Karniadakis G E 2016 Soft Matter 12 01
Google Scholar
[4] Tao Q, Luigi G R 2016 Mathematical Analysis Probability and Applications-Plenary Lectures (New York: Springer International Publishing) p2
[5] 王亮, 卢宇源, 安立佳 2017 应用化学 34 1250
Google Scholar
Wang L, Lu Y Y, An L J 2017 Chin. J. Appl. Chem. 34 1250
Google Scholar
[6] Hu C M, Zwanzig R 1974 J. Chem. Phys. 60 4354
Google Scholar
[7] Edward J T 1970 J. Chem. Educ. 47 261
Google Scholar
[8] Richardson S 2006 J. Fluid Mech. 59 707
[9] Ollila S T T, Smith C J, Ala-Nissila T, Denniston C 2013 Multiscale Model. Simul. 11 213
Google Scholar
[10] Vargas-Lara F, Starr F W, Douglas J F 2016 AIP Publishing LLC 1736 020080
Google Scholar
[11] Nisha M R, Philip J 2013 Phys. Scr. 88 15602
Google Scholar
[12] Velasco-Velez J J, Wu C H, Pascal T A, Wan L F, Guo J, Prendergast D, Salmeron M 2014 Science 346 831
Google Scholar
[13] Vasanthi R, Ravichandran S, Bagchi B 2001 J. Chem. Phys. 114 7989
Google Scholar
[14] Vasanthi R, Bhattacharyya S, Bagchi B 2002 J. Chem. Phys. 116 1092
Google Scholar
[15] 何昱辰, 刘向军 2014 力学学报 46 871
Google Scholar
He Y C, Liu X J 2014 Acta Mech. Sin. 46 871
Google Scholar
[16] Markutsya S, Subramaniam S, Vigil R D, Fox R O 2008 Ind. Eng. Chem. Res. 47 3338
Google Scholar
[17] Motohashi R, Hanasaki I, Ooi Y, Matsuda Y 2017 Micro Nano Lett. 12 506
Google Scholar
[18] Boyer D, Dean D S, Mejia-Monasterio C, Oshanin G 2012 Phys. Rev. E 86 60101
Google Scholar
[19] Xavier M 2010 Phys. Rev. E 82 041914
Google Scholar
[20] Abascal J L, Vega C 2005 J. Chem. Phys. 123 234505
Google Scholar
[21] Arnold A, Fahrenberger F, Holm C, Lenz O, Bolten M, Sutmann G 2013 Phys. Rev. E 88 63308
Google Scholar
[22] Folies S M, Baskets M I, Daw M S 1986 Phys. Rev. B 33 7983
Google Scholar
[23] Gonzalez M A, Abascal J L F 2010 J. Chem. Phys. 132 96101
Google Scholar
[24] Harris K R, Woolf L A 2004 J. Chem. Eng. Data 49 1064
Google Scholar
[25] Li T, Raizen M G 2013 Ann. Phys. 525 281
Google Scholar
[26] Ernst D, Kohler 2013 Phys. Chem. Chem. Phys. 15 845
Google Scholar
[27] Pranami G, Lamm M H 2015 J. Chem. Theory Comput. 11 4586
Google Scholar
[28] 张世良, 戚力, 高伟, 冯士东, 刘日平 2015 燕山大学学报 39 213
Google Scholar
Zhang S L, Qi L, Gao W, Feng S D, Liu R P 2015 J. Yanshan Univ. 39 213
Google Scholar
-
图 1 球形颗粒在不同边界条件下的平动摩擦系数, 颗粒向右运动 (a)黏性边界条件; (b)光滑边界条件
Figure 1. Translational friction coefficients of spherical particles under different boundary conditions and the particle move to the right: (a) Translational friction coefficient for stick boundary; (b) translational friction coefficient for slip boundary.
图 2 (a) Cu-H2O纳米流体的物理模型; (b) TIP4P/2005水分子结构示意图
Figure 2. (a) Physical model of Cu-H2O nanofluid; (b) schematic diagram of TIP4P/2005 water.
图 3 水分子模型的验证 (a) NPT系综下体系的温度随时间变化; (b) NPT系综下体系的总能量随时间变化
Figure 3. Validation of water molecular model: (a) Curve of temperature over time; (b) total energy of the system over time.
图 4 单颗粒布朗运动轨迹
Figure 4. Brownian motion trajectory of a single particle.
图 5 半径a = 1 nm的Cu颗粒在不同关联时间下扩散系数分布
Figure 5. Diffusion coefficient distribution of Cu particles with radius a =1 nm at different correlation time.
图 6 半径a = 1 nm的Cu纳米颗粒在采用不同拟合点拟合时扩散系数的变异系数, 关联时间Nt = 1363 ps
Figure 6. Variation coefficient of the diffusion coefficient of Cu nanoparticles with radius a =1 nm when different fitting points were used for fitting, correlation time Nt = 1363 ps.
图 7 纳米颗粒的平动扩散特性 (a)不同尺寸Cu纳米颗粒的平动扩散系数; (b)不同尺寸Cu纳米颗粒的平动摩擦因子
Figure 7. Translational diffusion characteristics of nanoparticles: (a) Translational diffusion coefficients of Cu nanoparticles with different sizes; (b) translational friction factors of Cu nanoparticles of different sizes.
图 8 颗粒旋转扩散系数计算的物理模型
Figure 8. Physical model for particle rotation diffusion coefficient calculation.
图 9 不同半径的Cu纳米颗粒的均方旋转角度
Figure 9. Mean-square rotation angles of Cu nanoparticles with different sizes.
图 10 颗粒旋转扩散特性 (a)颗粒的转动扩散系数; (b) 颗粒转动扩散摩擦因子
Figure 10. Rotational diffusion characteristics of particles: (a) Rotational diffusion coefficients of particle; (b) rotational friction factors of particle.
图 11 纳米颗粒周围水分子的RDF (a) RDF计算的物理模型; (b)不同尺寸的颗粒周围水分子的RDF曲线
Figure 11. Radial distribution function (RDF) of water molecules around nanoparticles: (a) Physical model for RDF calculation; (b) RDF curves of water molecules around particles of different sizes.
表 1 各工况下模拟域大小与原子数目
Table 1. The size of the simulation domain and number of atoms of different working conditions.
颗粒半
径/nmCu原
子数H2O分
子数总原
子数模拟域大小
Lx × Ly × Lz /Å30.5 43 971 2956 30 × 30 × 30 1.0 351 7380 23841 60 × 60 × 60 1.5 1199 7459 23576 60 × 60 × 60 2.0 2928 14381 45972 75 × 75 × 75 
DownLoad: CSV
表 2 Cu-H2O纳米流体势能参数
Table 2. Potential energy parameter of Cu-H2O nanofluid.
参数 取值 εo—o/eV 0.00803 σo—o/Å 3.1589 εCu—o /eV 0.052 σCu—o /Å 2.743
DownLoad: CSV
-
[1] Brown R 1828 Philos. Mag. 4 161
Google Scholar
[2] Einstein A 1905 Ann. Phys. 17 549
[3] Bian X, Kim C, Karniadakis G E 2016 Soft Matter 12 01
Google Scholar
[4] Tao Q, Luigi G R 2016 Mathematical Analysis Probability and Applications-Plenary Lectures (New York: Springer International Publishing) p2
[5] 王亮, 卢宇源, 安立佳 2017 应用化学 34 1250
Google Scholar
Wang L, Lu Y Y, An L J 2017 Chin. J. Appl. Chem. 34 1250
Google Scholar
[6] Hu C M, Zwanzig R 1974 J. Chem. Phys. 60 4354
Google Scholar
[7] Edward J T 1970 J. Chem. Educ. 47 261
Google Scholar
[8] Richardson S 2006 J. Fluid Mech. 59 707
[9] Ollila S T T, Smith C J, Ala-Nissila T, Denniston C 2013 Multiscale Model. Simul. 11 213
Google Scholar
[10] Vargas-Lara F, Starr F W, Douglas J F 2016 AIP Publishing LLC 1736 020080
Google Scholar
[11] Nisha M R, Philip J 2013 Phys. Scr. 88 15602
Google Scholar
[12] Velasco-Velez J J, Wu C H, Pascal T A, Wan L F, Guo J, Prendergast D, Salmeron M 2014 Science 346 831
Google Scholar
[13] Vasanthi R, Ravichandran S, Bagchi B 2001 J. Chem. Phys. 114 7989
Google Scholar
[14] Vasanthi R, Bhattacharyya S, Bagchi B 2002 J. Chem. Phys. 116 1092
Google Scholar
[15] 何昱辰, 刘向军 2014 力学学报 46 871
Google Scholar
He Y C, Liu X J 2014 Acta Mech. Sin. 46 871
Google Scholar
[16] Markutsya S, Subramaniam S, Vigil R D, Fox R O 2008 Ind. Eng. Chem. Res. 47 3338
Google Scholar
[17] Motohashi R, Hanasaki I, Ooi Y, Matsuda Y 2017 Micro Nano Lett. 12 506
Google Scholar
[18] Boyer D, Dean D S, Mejia-Monasterio C, Oshanin G 2012 Phys. Rev. E 86 60101
Google Scholar
[19] Xavier M 2010 Phys. Rev. E 82 041914
Google Scholar
[20] Abascal J L, Vega C 2005 J. Chem. Phys. 123 234505
Google Scholar
[21] Arnold A, Fahrenberger F, Holm C, Lenz O, Bolten M, Sutmann G 2013 Phys. Rev. E 88 63308
Google Scholar
[22] Folies S M, Baskets M I, Daw M S 1986 Phys. Rev. B 33 7983
Google Scholar
[23] Gonzalez M A, Abascal J L F 2010 J. Chem. Phys. 132 96101
Google Scholar
[24] Harris K R, Woolf L A 2004 J. Chem. Eng. Data 49 1064
Google Scholar
[25] Li T, Raizen M G 2013 Ann. Phys. 525 281
Google Scholar
[26] Ernst D, Kohler 2013 Phys. Chem. Chem. Phys. 15 845
Google Scholar
[27] Pranami G, Lamm M H 2015 J. Chem. Theory Comput. 11 4586
Google Scholar
[28] 张世良, 戚力, 高伟, 冯士东, 刘日平 2015 燕山大学学报 39 213
Google Scholar
Zhang S L, Qi L, Gao W, Feng S D, Liu R P 2015 J. Yanshan Univ. 39 213
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8310
- PDF Downloads: 203
- Cited By: 0
