Molecular dynamics simulation on dynamic behaviors of nanodroplets impinging on solid surfaces  decorated with nanopillars

Pan Ling; Zhang Hao; Lin Guo-Bin

doi:10.7498/aps.70.20210094

Abstract

Droplets’ impinging on a solid surface is a common phenomenon in industry and agriculture. With the development of micro and nano technology, the quantitative descriptions of impinging behaviors for nanodroplets are expected to be further explored. Molecular dynamics (MD) simulation is adopted to investigate the behaviors of water nanodroplets impinging on cooper surfaces which have been decorated with square nanopillars. The dynamical characteristics of nanodroplets are analyzed at 5 different pillar heights, 6 different surface characteristic energy values, and a wide range of droplet velocities. The results show that there is no obvious difference among the dynamical behaviors for nanodroplets, whose radii are in a range from 35 to 45 Å, impinging on a solid surface. With the increase of droplet velocity, the wetting pattern of steady nanodroplets first transfers from Cassie state (V₀ = 2–3 Å/ps) to Wenzel state (V₀ = 4–10 Å/ps), then it returns to the Cassie state (V₀ = 11–13 Å/ps) again. Nanodroplets bounce off the solid surface when V₀ > 13 Å/ps. The relationship between the maximum spreading time and droplet velocity is presented. Inflection points in the curve of the relationship are discovered and their formation mechanism is studied. The spreading factors of steady states for nanodroplets with velocity lower than 9 Å/ps are nearly the same; however, they decrease gradually for nanodroplets with velocity higher than 9 Å/ps. In addition, the increasing height of square nanopillars facilitates the transition from Wenzel state to Cassie state and reduces the spreading radius of steady nanodroplets. The mechanism, which yields Wenzel state when the nanodroplets impinge on solid surface with lower height nanopillars, is investigated. In the spreading stage, spreading radii of nanodroplets impinging on surfaces with different height nanopillars are almost identical. The influence of nanopillar height mainly plays a role in the retraction stage of droplets and it fades away as the height further increases. Moreover, the higher surface characteristic energy benefits the spreading of nanodroplets and reduces the retraction time. Especially, nanodroplets do not experience retraction stage, and the spreading stage is kept until the nanodroplets reach a stable state when the surface characteristic energy is increased to 0.714 kcal/mol. Compared with the spreading factor, the centroid height of nanodroplet is very sensitive to the change of surface characteristic energy.

Keywords:

Authors and contacts

School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350108, China

Corresponding author: Pan Ling, panling@fzu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51875105, 51875106), the Industry-Academy Cooperation Project of Fujian Province (Grant No. 2020H6025), and the Scientific Research Program of the Jinjiang Science and Education Park Development Center Fuzhou University, China (Grant No. 2019-JJFDKY-54).

FullText HTML : translate this paragraph

References

[1]	Galliker P, Schneider J, Eghlidi H, Kress S, Sandoghdar V, Poulikakos D 2012 Nat. Commun. 3 782 Google Scholar
[2]	Bergeron V, Bonn D, Martin J Y, Vovelle L 2000 Nature 405 772 Google Scholar
[3]	Zhou Z F, Chen B, Wang R, Wang G X 2017 Exp. Therm. Fluid Sci. 82 189 Google Scholar
[4]	Chen X L, Li X M, Shao J Y, An N L, Tian H M, Wang C, Han T Y, Wang L, Lu B H 2017 Small 13 1604245 Google Scholar
[5]	Pan K L, Chou P C, Tseng Y J 2009 Phys. Rev. E 80 036301 Google Scholar
[6]	Deng X, Mammen L, Butt H, Vollmer D 2012 Science 335 67 Google Scholar
[7]	Wang N, Xiong D S, Deng Y L, Shi Y, Wang K 2015 ACS. Appl. Mater. Interfaces 7 6260 Google Scholar
[8]	Peng Y, He Y X, Yang S A, Ben S, Cao M Y, Li K, Liu K, Jiang L 2015 Adv. Funct. Mater. 25 5967 Google Scholar
[9]	Rioboo R, Tropea C, Marengo M 2001 Atomization Spray. 11 155 Google Scholar
[10]	施其明, 贾志海, 林琪焱 2016 化工进展 35 3818 Google Scholar Shi Q M, Jia Z H, Lin Q Y 2016 Chem. Ind. Eng. Prog. 35 3818 Google Scholar
[11]	彭家略, 郭浩, 尤天涯, 纪献兵, 徐进良 2021 70 044701 Google Scholar Peng J L, Guo H, You T Y, Ji X B, Xu J L 2021 Acta Phys. Sin. 70 044701 Google Scholar
[12]	顾秦铭, 张朝阳, 周晖, 张凯峰, 徐坤, 朱浩 2020 机械工程学报 56 223 Google Scholar Gu Q M, Zhang C Y, Zhou H, Zhang K F, Xu K, Zhu H 2020 J. Mech. Eng. 56 223 Google Scholar
[13]	Qi H C, Wang T Y, Che Z Z 2020 Phys. Rev. E 101 043114 Google Scholar
[14]	Gao S, Liao Q W, Liu W, Liu Z C 2018 J. Phys. Chem. Lett. 9 13 Google Scholar
[15]	Gao S, Liao Q W, Liu W, Liu Z C 2017 Langmuir 33 12379 Google Scholar
[16]	Xie F F, Lv S H, Yang Y R, Wang X D 2020 J. Phys. Chem. Lett. 11 2818 Google Scholar
[17]	邱丰, 王猛, 周化光, 郑璇, 林鑫, 黄卫东 2013 62 120203 Google Scholar Qiu F, Wang M, Zhou H G, Zheng X, Lin X, Huang W D 2013 Acta Phys. Sin. 62 120203 Google Scholar
[18]	Liu H Y, Chu F Q, Zhang J, Wen D S 2020 Phys. Rev. Fluids 5 074201 Google Scholar
[19]	Wang Y B, Wang X D, Yang Y R, Chen M 2019 J. Phys. Chem. C. 123 12841 Google Scholar
[20]	Yin Z J, Ding Z L, Zhang W F, Su R, Chai F T, Yu P 2020 Comput. Mater. Sci. 183 109814 Google Scholar
[21]	Zhang M Y, Ma L J, Wang Q, Hao P, Zheng X 2020 Colloids Surf., A 604 125291 Google Scholar
[22]	Jorgensen W L, Chandrasekhar J, Madura J D, Impey R W, Klein M L 1983 J. Chem. Phys. 79 926 Google Scholar
[23]	Fu T, Wu N, Lu C, Wang J B, Wang Q L 2019 Mol. Simul. 45 35 Google Scholar
[24]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[25]	Song F H, Li B Q, Li Y 2015 Phys. Chem. Chem. Phys. 17 5543 Google Scholar
[26]	Gonzalez-Valle C U, Kumar S, Ramos-Alvarado B 2018 The Journal of Physical Chemistry C 122 7179 Google Scholar
[27]	Koishi T, Yasuoka K, Zeng X C 2017 Langmuir 33 10184 Google Scholar
[28]	Cordeiro J, Desai S 2017 ASME J. Micro Nano-Manuf. 5 031008 Google Scholar
[29]	向恒 2008 博士学位论文 (北京: 清华大学) Xiang H 2008 Ph. D. Dissertation (Beijing: Tsinghua University) (in Chinese)
[30]	Chen L, Wang S Y, Xiang X, Tao W Q 2020 Comput. Mater. Sci. 171 109223 Google Scholar
[31]	陈正隆 2007 分子模拟的实践与理论 (北京: 化学工业出版社) 第8页 Chen Z L 2007 Practice and Theory of Molecular Simulations (Beijing: Chemical Industry Press) p8 (in Chinese)
[32]	Bekele S, Evans O G, Tsige M 2020 J. Phys. Chem.C. 124 20109 Google Scholar
[33]	Essmann U, Perera L, Berkowitz M, Darden T, Lee H, Pedersen L 1995 J. Chem. Phys. 103 8577
[34]	Hoover W G 1985 Phys. Rev. A 31 1695 Google Scholar
[35]	Song F H, Li B Q, Liu C 2013 Langmuir 29 4266 Google Scholar
[36]	章佳健 2020 博士学位论文 (合肥: 中国科学技术大学) Zhang J J 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[37]	成中军, 杜明, 来华, 张乃庆, 孙克宁 2013 高等学校化学学报 34 606 Google Scholar Cheng Z J, Du M, Lai H, Zhang N Q, Sun K N 2013 Chem. J. Chin. Univ. 34 606 Google Scholar
[38]	Hu H B, Chen L B, Bao L Y, Huang S H 2014 Chin. Phys. B. 23 074702 Google Scholar
[39]	Wenzel R N 1936 Ind. Eng. Chem. 28 988 Google Scholar
[40]	Cassie A B D, Baxter S 1944 Trans. Farad. Soc. 40 546 Google Scholar
[41]	焦云龙, 刘小君, 刘焜 2016 力学学报 48 353 Google Scholar Jiao Y L, Liu X J, Liu K 2016 Chin J. Theor. Appl. Mech. 48 353 Google Scholar

Cited By

图 1 模拟体系的初始构型

Figure 1. Initial configuration of the simulation system.

DownLoad: Full-Size Img PowerPoint

图 2 液滴右半部分密度云图

Figure 2. Density profile of the right-sided droplet.

DownLoad: Full-Size Img PowerPoint

图 3 液滴尺寸对铺展时间t的影响　(a) 液滴在光滑固体表面上; (b) 液滴在柱状固体表面上

Figure 3. Effects of droplets size on spreading time: (a) Droplets on the flat solid surfaces; (b) droplets on the nanopillared solid surfaces.

DownLoad: Full-Size Img PowerPoint

图 4 不同速度的液滴撞击柱状固体表面的动态行为

Figure 4. Dynamic behaviors of droplets with various velocities impinging on nanopillared solid surfaces.

DownLoad: Full-Size Img PowerPoint

图 5 液滴质心高度h随铺展时间t的变化

Figure 5. Time evolution of central height of droplets with different velocities.

DownLoad: Full-Size Img PowerPoint

图 6 最大铺展时间t_max随速度V₀的变化

Figure 6. The dependence of the maximum spreading time of droplets on velocities.

DownLoad: Full-Size Img PowerPoint

图 7 不同速度液滴的最大铺展状态

Figure 7. The maximum spreading states of droplets with different velocities.

DownLoad: Full-Size Img PowerPoint

图 8 不同初始速度的液滴铺展因子β随时间t的变化　(a) V₀ = 3—9 Å/ps; (b) V₀ = 11—15 Å/ps

Figure 8. Time evolution of spreading factor for droplets with different velocities: (a) V₀ = 3−9 Å/ps; (b) V₀ = 11−15 Å/ps.

DownLoad: Full-Size Img PowerPoint

图 9 不同初始速度液滴的最大铺展因子β_max

Figure 9. The maximum spreading factor of droplets with different velocities.

DownLoad: Full-Size Img PowerPoint

图 10 液滴撞击不同方柱高度固体表面的稳定状态

Figure 10. Steady states of droplets impinging on solid surfaces with nanopillars of different height.

DownLoad: Full-Size Img PowerPoint

图 11 不同时刻液滴底部z坐标

Figure 11. Time evolution of z coordinates for the bottom of droplets.

DownLoad: Full-Size Img PowerPoint

图 12 不同方柱高度对液滴质心高度的影响

Figure 12. Effects of nanopillars with different height on centroid height of droplets.

DownLoad: Full-Size Img PowerPoint

图 13 方柱高度对铺展因子的影响

Figure 13. Dependence of spreading factor on the height of nanopillars.

DownLoad: Full-Size Img PowerPoint

图 14 方柱高度对铺展半径R的影响

Figure 14. Dependence of spreading radius on the height of nanopillars.

DownLoad: Full-Size Img PowerPoint

图 15 液滴撞击不同特征能柱状固体表面的质心高度

Figure 15. Centroid height of droplets impinging on surfaces with different characteristic energy.

DownLoad: Full-Size Img PowerPoint

图 16 液滴撞击具有不同特征能方柱表面时的铺展因子

Figure 16. Time evolution of spreading factor of droplets impinging on surfaces with different characteristic energy.

DownLoad: Full-Size Img PowerPoint

表 1 液滴撞击柱状固体表面稳定状态时的润湿模式

Table 1. Wetting patterns of steady state of droplets impinging on nanopillared solid surfaces.

V₀/(Å·ps^–1)	2—3	4—10	11—13	14—15
润湿模式	Cassie	Wenzel	Cassie	弹跳

DownLoad: CSV

表 2 液滴撞击不同高度柱状表面后的稳定态润湿模式

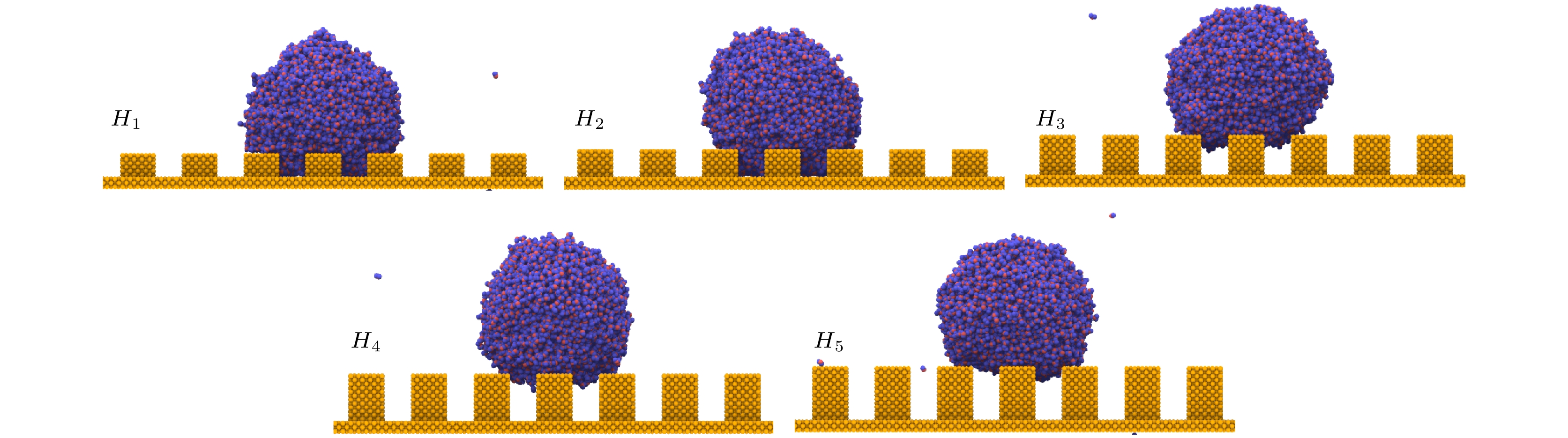
Table 2. Wetting patterns of steady state of droplets impinging on surfaces with different height nanopillars.

方柱高度	H₁	H₂	H₃	H₄	H₅
方柱高度	10.845 Å	14.460 Å	18.075 Å	21.690 Å	25.305 Å
润湿模式	Wenzel	Wenzel	Cassie	Cassie	Cassie

DownLoad: CSV

表 3 不同${\varepsilon _{\rm{s}}}$固体表面对应的${\varepsilon _{{\rm{s \text- o}}}}$及液滴接触角$ \theta $

Table 3. Corresponding ${\varepsilon _{{\rm{s \text- o}}}}$ and contact angles of droplets for solid surfaces with different ${\varepsilon _{\rm{s}}}$.

${\varepsilon _{\rm{s}}}$/(kcal·mol^–1)	${\varepsilon _{\rm{s}}}$/(kcal·mol^–1)	接触角$ \theta $/$ (°) $
${\varepsilon _{{\rm{s1}}}} = 0.5{\varepsilon _{{\rm{Cu}}}} = 0.119$	0.139	125.9
${\varepsilon _{{\rm{s2}}}} = 1.5{\varepsilon _{{\rm{Cu}}}} = 0.357$	0.241	97.1
${\varepsilon _{{\rm{s3}}}} = 2.0{\varepsilon _{{\rm{Cu}}}} = 0.476$	0.278	80
${\varepsilon _{{\rm{s4}}}} = 3.0{\varepsilon _{{\rm{Cu}}}} = 0.714$	0.341	63
${\varepsilon _{{\rm{s5}}}} = 4.0{\varepsilon _{{\rm{Cu}}}} = 0.952$	0.394	45
${\varepsilon _{{\rm{s6}}}} = 5.0{\varepsilon _{{\rm{Cu}}}} = 1.190$	0.440	22

DownLoad: CSV

map

[1]	Galliker P, Schneider J, Eghlidi H, Kress S, Sandoghdar V, Poulikakos D 2012 Nat. Commun. 3 782 Google Scholar
[2]	Bergeron V, Bonn D, Martin J Y, Vovelle L 2000 Nature 405 772 Google Scholar
[3]	Zhou Z F, Chen B, Wang R, Wang G X 2017 Exp. Therm. Fluid Sci. 82 189 Google Scholar
[4]	Chen X L, Li X M, Shao J Y, An N L, Tian H M, Wang C, Han T Y, Wang L, Lu B H 2017 Small 13 1604245 Google Scholar
[5]	Pan K L, Chou P C, Tseng Y J 2009 Phys. Rev. E 80 036301 Google Scholar
[6]	Deng X, Mammen L, Butt H, Vollmer D 2012 Science 335 67 Google Scholar
[7]	Wang N, Xiong D S, Deng Y L, Shi Y, Wang K 2015 ACS. Appl. Mater. Interfaces 7 6260 Google Scholar
[8]	Peng Y, He Y X, Yang S A, Ben S, Cao M Y, Li K, Liu K, Jiang L 2015 Adv. Funct. Mater. 25 5967 Google Scholar
[9]	Rioboo R, Tropea C, Marengo M 2001 Atomization Spray. 11 155 Google Scholar
[10]	施其明, 贾志海, 林琪焱 2016 化工进展 35 3818 Google Scholar Shi Q M, Jia Z H, Lin Q Y 2016 Chem. Ind. Eng. Prog. 35 3818 Google Scholar
[11]	彭家略, 郭浩, 尤天涯, 纪献兵, 徐进良 2021 70 044701 Google Scholar Peng J L, Guo H, You T Y, Ji X B, Xu J L 2021 Acta Phys. Sin. 70 044701 Google Scholar
[12]	顾秦铭, 张朝阳, 周晖, 张凯峰, 徐坤, 朱浩 2020 机械工程学报 56 223 Google Scholar Gu Q M, Zhang C Y, Zhou H, Zhang K F, Xu K, Zhu H 2020 J. Mech. Eng. 56 223 Google Scholar
[13]	Qi H C, Wang T Y, Che Z Z 2020 Phys. Rev. E 101 043114 Google Scholar
[14]	Gao S, Liao Q W, Liu W, Liu Z C 2018 J. Phys. Chem. Lett. 9 13 Google Scholar
[15]	Gao S, Liao Q W, Liu W, Liu Z C 2017 Langmuir 33 12379 Google Scholar
[16]	Xie F F, Lv S H, Yang Y R, Wang X D 2020 J. Phys. Chem. Lett. 11 2818 Google Scholar
[17]	邱丰, 王猛, 周化光, 郑璇, 林鑫, 黄卫东 2013 62 120203 Google Scholar Qiu F, Wang M, Zhou H G, Zheng X, Lin X, Huang W D 2013 Acta Phys. Sin. 62 120203 Google Scholar
[18]	Liu H Y, Chu F Q, Zhang J, Wen D S 2020 Phys. Rev. Fluids 5 074201 Google Scholar
[19]	Wang Y B, Wang X D, Yang Y R, Chen M 2019 J. Phys. Chem. C. 123 12841 Google Scholar
[20]	Yin Z J, Ding Z L, Zhang W F, Su R, Chai F T, Yu P 2020 Comput. Mater. Sci. 183 109814 Google Scholar
[21]	Zhang M Y, Ma L J, Wang Q, Hao P, Zheng X 2020 Colloids Surf., A 604 125291 Google Scholar
[22]	Jorgensen W L, Chandrasekhar J, Madura J D, Impey R W, Klein M L 1983 J. Chem. Phys. 79 926 Google Scholar
[23]	Fu T, Wu N, Lu C, Wang J B, Wang Q L 2019 Mol. Simul. 45 35 Google Scholar
[24]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[25]	Song F H, Li B Q, Li Y 2015 Phys. Chem. Chem. Phys. 17 5543 Google Scholar
[26]	Gonzalez-Valle C U, Kumar S, Ramos-Alvarado B 2018 The Journal of Physical Chemistry C 122 7179 Google Scholar
[27]	Koishi T, Yasuoka K, Zeng X C 2017 Langmuir 33 10184 Google Scholar
[28]	Cordeiro J, Desai S 2017 ASME J. Micro Nano-Manuf. 5 031008 Google Scholar
[29]	向恒 2008 博士学位论文 (北京: 清华大学) Xiang H 2008 Ph. D. Dissertation (Beijing: Tsinghua University) (in Chinese)
[30]	Chen L, Wang S Y, Xiang X, Tao W Q 2020 Comput. Mater. Sci. 171 109223 Google Scholar
[31]	陈正隆 2007 分子模拟的实践与理论 (北京: 化学工业出版社) 第8页 Chen Z L 2007 Practice and Theory of Molecular Simulations (Beijing: Chemical Industry Press) p8 (in Chinese)
[32]	Bekele S, Evans O G, Tsige M 2020 J. Phys. Chem.C. 124 20109 Google Scholar
[33]	Essmann U, Perera L, Berkowitz M, Darden T, Lee H, Pedersen L 1995 J. Chem. Phys. 103 8577
[34]	Hoover W G 1985 Phys. Rev. A 31 1695 Google Scholar
[35]	Song F H, Li B Q, Liu C 2013 Langmuir 29 4266 Google Scholar
[36]	章佳健 2020 博士学位论文 (合肥: 中国科学技术大学) Zhang J J 2020 Ph. D. Dissertation (Hefei: University of Science and Technology of China) (in Chinese)
[37]	成中军, 杜明, 来华, 张乃庆, 孙克宁 2013 高等学校化学学报 34 606 Google Scholar Cheng Z J, Du M, Lai H, Zhang N Q, Sun K N 2013 Chem. J. Chin. Univ. 34 606 Google Scholar
[38]	Hu H B, Chen L B, Bao L Y, Huang S H 2014 Chin. Phys. B. 23 074702 Google Scholar
[39]	Wenzel R N 1936 Ind. Eng. Chem. 28 988 Google Scholar
[40]	Cassie A B D, Baxter S 1944 Trans. Farad. Soc. 40 546 Google Scholar
[41]	焦云龙, 刘小君, 刘焜 2016 力学学报 48 353 Google Scholar Jiao Y L, Liu X J, Liu K 2016 Chin J. Theor. Appl. Mech. 48 353 Google Scholar

[1]	Ming Zhi-Fei, Song Hai-Yang, An Min-Rong. Mechanical behavior of graphene magnesium matrix composites based on molecular dynamics simulation. Acta Physica Sinica, 2022, 71(8): 086201. doi: 10.7498/aps.71.20211753
[2]	Zhao Chang, Ji Xian-Bing, Yang Yu-Hao, Meng Yu-Hang, Xu Jin-Liang, Peng Jia-Lue. Behavior characteristics of Janus particles impacting bubbles. Acta Physica Sinica, 2022, 71(21): 214701. doi: 10.7498/aps.71.20220632
[3]	Wei Guo-Cui, Tian Ze-An. Molecular dynamics simulation of rapid solidification of Cu₆₄Zr₃₆ nanodrops of different sizes. Acta Physica Sinica, 2021, 70(24): 246401. doi: 10.7498/aps.70.20211235
[4]	Zhou Bian, Yang Liang. Molecular dynamics simulation of effect of cooling rate on the microstructures and deformation behaviors in metallic glasses. Acta Physica Sinica, 2020, 69(11): 116101. doi: 10.7498/aps.69.20191781
[5]	Tang Peng-Bo, Wang Guan-Qing, Wang Lu, Shi Zhong-Yu, Li Yuan, Xu Jiang-Rong. Experimental investigation on dynamic behavior of single droplet impcating normally on dry sphere. Acta Physica Sinica, 2020, 69(2): 024702. doi: 10.7498/aps.69.20191141
[6]	Yang Ya-Jing, Mei Chen-Xi, Zhang Xu-Dong, Wei Yan-Ju, Liu Sheng-Hua. Kinematics and passing modes of a droplet impacting on a soap film. Acta Physica Sinica, 2019, 68(15): 156101. doi: 10.7498/aps.68.20190604
[7]	Dong Qi-Qi, Hu Hai-Bao, Chen Shao-Qiang, He Qiang, Bao Lu-Yao. Molecular dynamics simulation of freezing process of water droplets impinging on cold surface. Acta Physica Sinica, 2018, 67(5): 054702. doi: 10.7498/aps.67.20172174
[8]	Hu Hai-Bao, He Qiang, Yu Si-Xiao, Zhang Zhao-Zhu, Song Dong. Freezing behavior of droplet impacting on cold surfaces. Acta Physica Sinica, 2016, 65(10): 104703. doi: 10.7498/aps.65.104703
[9]	Li Yan-Ru, He Qiu-Xiang, Wang Fang, Xiang Lang, Zhong Jian-Xin, Meng Li-Jun. Dynamical evolution study of metal nanofilms on graphite substrates. Acta Physica Sinica, 2016, 65(3): 036804. doi: 10.7498/aps.65.036804
[10]	Xu Wei, Lan Zhong, Peng Ben-Li, Wen Rong-Fu, Ma Xue-Hu. Molecular dynamics simulation on the wetting characteristic of micro-droplet on surfaces with different free energies. Acta Physica Sinica, 2015, 64(21): 216801. doi: 10.7498/aps.64.216801
[11]	Si Li-Na, Wang Xiao-Li. A molecular dynamics study on adhesive contact processes of surfaces with nanogrooves. Acta Physica Sinica, 2014, 63(23): 234601. doi: 10.7498/aps.63.234601
[12]	Sun Wei-Feng, Wang Xuan. Molecular dynamics simulation study of polyimide/copper-nanoparticle composites. Acta Physica Sinica, 2013, 62(18): 186202. doi: 10.7498/aps.62.186202
[13]	Chen Qing, Sun Min-Hua. Molecular dynamics simulation of isothermal crystallization dynamics in Cu nanocluster. Acta Physica Sinica, 2013, 62(3): 036101. doi: 10.7498/aps.62.036101
[14]	Ge Song, Chen Min. A molecular dynamics simulation on the relationship between contact angle and solid-liquid interfacial thermal resistance. Acta Physica Sinica, 2013, 62(11): 110204. doi: 10.7498/aps.62.110204
[15]	Xia Dong, Wang Xin-Qiang. Structures and melting behaviors of ultrathin platinum nanowires. Acta Physica Sinica, 2012, 61(13): 130510. doi: 10.7498/aps.61.130510
[16]	Bi Fei-Fei, Guo Ya-Li, Shen Sheng-Qiang, Chen Jue-Xian, Li Yi-Qiao. Experimental study of spread characteristics of droplet impacting solid surface. Acta Physica Sinica, 2012, 61(18): 184702. doi: 10.7498/aps.61.184702
[17]	Wang Jun, Zhang Bao-Ling, Zhou Yu-Lu, Hou Qing. Molecular dynamics simulation of helium behavior in tungsten matrix. Acta Physica Sinica, 2011, 60(10): 106601. doi: 10.7498/aps.60.106601
[18]	Xie Fang, Zhu Ya-Bo, Zhang Zhao-Hui, Zhang Lin. Molecular dynamics simulation of multi-wall carbon nanotube oscillators. Acta Physica Sinica, 2008, 57(9): 5833-5837. doi: 10.7498/aps.57.5833
[19]	Meng Li-Jun, Zhang Kai-Wang, Zhong Jian-Xin. Molecular dynamics simulation of formation of silicon nanoparticles on surfaces of carbon nanotubes. Acta Physica Sinica, 2007, 56(2): 1009-1013. doi: 10.7498/aps.56.1009
[20]	Li Rui, Hu Yuan-Zhong, Wang Hui, Zhang Yu-Jun. Molecular dynamics simulation of motion of single-walled carbon nanotubes on graphite substrate. Acta Physica Sinica, 2006, 55(10): 5455-5459. doi: 10.7498/aps.55.5455

Catalog

Vol. 70, Issue 13 - 2021-07-05

Metrics

Abstract views: 5483
PDF Downloads: 127
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板