-
To further explore the complex dynamical behaviors in coexisting attractors, a fourth-order chaotic system with four types of coexisting attractors and four unstable equilibrium points is constructed in this paper. The dynamic behavior of the new system is analyzed by means of phase trajectory diagram, time domain waveform diagram, Poincaré map, Lyapunov exponent spectrum and bifurcation diagram. The experimental results show that as the parameters change, the system exhibits rich dynamic behaviors such as stable points, period-doubling bifurcations, coexisting bifurcation modes, and chaotic crises. When the system parameters and memristive parameters change, it is found that the system has different types of coexisting attractors, such as the coexistence of two periodic attractors, the coexistence of two single-scroll chaotic attractors, the coexistence of two double-scroll chaotic attractors, the coexistence of two point attractors. In particular, the system also has the rotation phenomenon of coexisting attractors. Finally, a nonlinear feedback controller is designed, which can make the new system achieve chaos synchronization in a short time. The phase diagram captured by the field-programmable gate array (FPGA) hardware platform is consistent with the numerical simulation results, which proves the feasibility of the system.
-
Keywords:
- chaotic system /
- coexistence attractor /
- rotating attractor /
- field-programmable gate array
[1] Tucker W 1999 Comptes Rendus de l'Académie des Sciences-Series I-Mathematics 328 1197
[2] Chen G R, Ueta T 1999 Int. J. Bifur. Chaos 9 1465
 Google Scholar
Google Scholar
[3] Lü J H, Chen G R 2002 Int. J. Bifur. Chaos 12 659
 Google Scholar
Google Scholar
[4] Bao B C, Liu Z, Xu J P 2009 J. Syst. Eng. Electron 20 1179
 Google Scholar
Google Scholar
[5] Lai Q, Wang Z L, Kamdem P D K 2022 Mod Phys. Lett. B 36 1
 Google Scholar
Google Scholar
[6] Liu M T, Yu W X, Wang J N, Chen Y, Bian Y Y 2022 Circuit World 48 1
 Google Scholar
Google Scholar
[7] 刘嵩, 韦亚萍, 刘静漪, 张国平 2020 华中师范大学学报 (自然科学版) 54 36
 Google Scholar
Google Scholar
Liu S, Wei Y P, Liu J Y, Zhang G P 2020 J. Cent. Chin. Normal Univ. (Nat. Sci.) 54 36
 Google Scholar
Google Scholar
[8] 庄志本, 李军, 刘静漪, 陈世强 2020 69 50
 Google Scholar
Google Scholar
Zhuang Z B, Li J, Liu J Y, Chen S Q 2020 Acta Phys. Sin. 69 50
 Google Scholar
Google Scholar
[9] 吴庆庆, 郑雅婷, 李涛 2014 中国科技论文 9 130
 Google Scholar
Google Scholar
Wu Q Q, Zheng Y T, Li T 2014 Science Paper Online 9 130
 Google Scholar
Google Scholar
[10] 颜闽秀, 林建峰, 谢俊红 2021 南京邮电大学学报(自然科学版) 41 66
Yan M X, Lin J F, Xie J H 2021 J. Nanjing Youdian Univ. (Nat. Sci.) 41 66
[11] Chua L O 1971 IEEE Trans. Circuits Theor. 18 507
 Google Scholar
Google Scholar
[12] Strukov D B, Snider G S, Stewart D R, Stanley W R 2008 Nature 453 80
 Google Scholar
Google Scholar
[13] Wang M J, Deng Y, Liao X H, Li Z J, Ma M L, Zeng Y C 2019 Int. J. Nonlin. Mech. 111 149
 Google Scholar
Google Scholar
[14] 徐昌彪, 何颖辉, 吴霞, 莫运辉 2020 哈尔滨工业大学学报 52 92
 Google Scholar
Google Scholar
Xu C B, He Y H, Wu X, Mo Y H 2020 J. Harbin Eng. Univ. 52 92
 Google Scholar
Google Scholar
[15] Hu H Y, Cao Y H, Hao J, Li X J, Mou J 2022 Multimed. Tools Appl. 82 4343
 Google Scholar
Google Scholar
[16] Guo Z G, Wen J J, Mou J 2022 Mathematics 11 1
[17] 鲜永菊, 莫运辉, 徐昌彪, 吴霞, 何颖辉 2020 华南理工大学学报(自然科学版) 48 32
 Google Scholar
Google Scholar
Xian Y J, Mo Y H, Xu C B, Wu X, He Y H 2020 J. Huanan Ligong Univ. (Nat. Sci.) 48 32
 Google Scholar
Google Scholar
[18] 王徐盱, 张宏昊, 赖强 2021 电子元件与材料 40 1208
 Google Scholar
Google Scholar
Wang X X, Zhang H H, Lai Q 2021 Electron. Components Mater. 40 1208
 Google Scholar
Google Scholar
[19] 鲜永菊, 扶坤荣, 徐昌彪 2021 振动与冲击 40 15
 Google Scholar
Google Scholar
Xian Y J, Fu K R, Xu C B 2021 J. Vibr. Shock 40 15
 Google Scholar
Google Scholar
[20] 李木子, 许荣今, 岳立娟 2021 东北师大学报(自然科学版) 53 120
 Google Scholar
Google Scholar
Li M Z, Xu R J, Yue L J 2021 J. Dongbei Shida Univ. (Nat. Sci.) 53 120
 Google Scholar
Google Scholar
[21] 闵富红, 王珠林, 曹戈, 王恩荣 2018 电子学报 46 9
 Google Scholar
Google Scholar
Min F H, Wang Z L, Cao G, Wang E R 2018 Acta Electronica Sin. 46 9
 Google Scholar
Google Scholar
[22] Ma X J, Mou J, Li X, Banerjee S, Cao Y H, Wang J Y 2021 Chaos Solit. Frac. 152 111363
 Google Scholar
Google Scholar
[23] Bao H, Wang N, Bao B C, Chen M, Jin P P, Wang G Y 2018 Commun. Nonlinear Sci. 57 264
 Google Scholar
Google Scholar
[24] Yu F, Liu L, Qian S, Li L X, Huang Y Y, Shi C Q, Cai S, Wu X M, Du S C, Wan Q Z 2020 Complexity 2020 1
 Google Scholar
Google Scholar
[25] 李晓霞, 郑驰, 王雪, 曹樱子, 徐桂芝 2022 哈尔滨工业大学学报 69 163
 Google Scholar
Google Scholar
Li X X, Zheng C, Wang X, Cao Y Z, Xu G Z 2022 J. Harbin Eng. Univ. 69 163
 Google Scholar
Google Scholar
[26] 秦铭宏, 赖强, 吴永红 2022 71 160502
 Google Scholar
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
 Google Scholar
Google Scholar
[27] Li Q D, Zeng H Z, Li J 2015 Nonlinear Dyn. 79 2295
 Google Scholar
Google Scholar
[28] Yang Q G, Wei Z C, Chen G R 2010 Int. J. Bifur. Chao 20 1061
 Google Scholar
Google Scholar
[29] 孙克辉, 汪艳, 刘璇 2013 电路与系统学报 18 500
 Google Scholar
Google Scholar
Sun K H, Wang Y, Liu X 2013 J. Circuits Syst. 18 500
 Google Scholar
Google Scholar
[30] 陈志盛, 孙克辉, 张泰山 2005 6 2580
 Google Scholar
Google Scholar
Chen Z S, Sun K H, Zhang T S 2005 Acta Phys. Sin. 6 2580
 Google Scholar
Google Scholar
[31] 付景超, 张中华 2016 控制与决策 31 1707
 Google Scholar
Google Scholar
Fu J C, Zhang Z H 2016 Control Decision 31 1707
 Google Scholar
Google Scholar
[32] 毛北行, 王东晓, 卜春霞 2012 华中师范大学学报(自然科学版) 46 297
 Google Scholar
Google Scholar
Mao B X, Wang D X, Bu C X 2012 J. Cent. Chin. Normal Univ. (Nat. Sci.) 46 297
 Google Scholar
Google Scholar
-
图 5 取
$ a $ 的不同值在x-y平面的相位图 (a)周期1吸引子共存(a = 3); (b)周期2吸引子共存(a = 3.2); (c)单涡卷混沌吸引子共存(a = 34.93); (d)周期1吸引子共存 (a = 50)Figure 5. The phase diagram of different values in x-y plane: (a) Coexistence period 1 attractor coexistence (a = 3); (b) coexistence period 2 attractor coexistence (a = 3.2); (c) coexisting single scroll chaotic attractor (a = 34.93); (d) coexistence period 1 attractor coexistence (a = 50).
图 7 取
$ b $ 的不同值在x-y平面的相位图 (a) 周期1吸引子共存(b = 10); (b) 周期2吸引子共存(b = 20.5); (c) 双涡卷混沌吸引子共存(b = 62); (d) 单涡卷吸引子共存(b = 70)Figure 7. Phase diagram of different values of parameter
$ b $ on x-y plane: (a) Coexisting period 1 attractor coexistence (b = 10); (b) coexisting period 2 attractor coexistence (b = 20.5); (c) coexisting double scroll chaotic attractor coexistence (b = 62); (d) coexisting single-scroll attractors coexistence (b = 70).表 1 不同
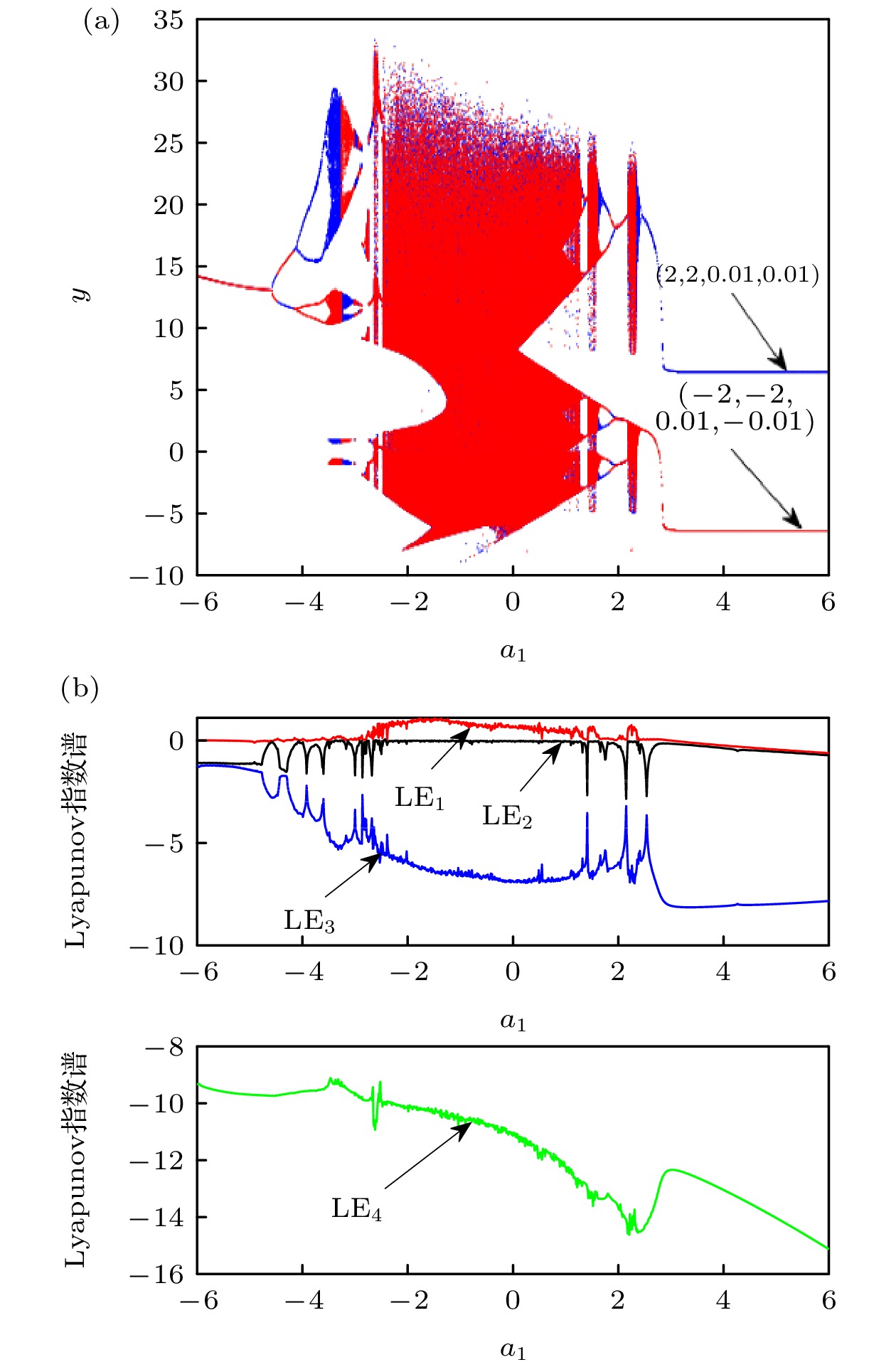
$ {a_1} $ 值下的共存吸引子类型及图形编号Table 1. Types and figure numbers of coexisting attractors under different
$ {a_1} $ values.参数$ {a_1} $ 运动状态 图9 –3.51 周期4 (a) –3.30 单涡卷混沌 (b) –3.23 单涡卷混沌 (c) –2.73 周期1 (d) –2.72 周期1 (e) –2.75 双涡卷混沌 (f) –2.38 周期2 (g) 1.60 混沌 (h) 3.01 稳定点 (i) -
[1] Tucker W 1999 Comptes Rendus de l'Académie des Sciences-Series I-Mathematics 328 1197
[2] Chen G R, Ueta T 1999 Int. J. Bifur. Chaos 9 1465
 Google Scholar
Google Scholar
[3] Lü J H, Chen G R 2002 Int. J. Bifur. Chaos 12 659
 Google Scholar
Google Scholar
[4] Bao B C, Liu Z, Xu J P 2009 J. Syst. Eng. Electron 20 1179
 Google Scholar
Google Scholar
[5] Lai Q, Wang Z L, Kamdem P D K 2022 Mod Phys. Lett. B 36 1
 Google Scholar
Google Scholar
[6] Liu M T, Yu W X, Wang J N, Chen Y, Bian Y Y 2022 Circuit World 48 1
 Google Scholar
Google Scholar
[7] 刘嵩, 韦亚萍, 刘静漪, 张国平 2020 华中师范大学学报 (自然科学版) 54 36
 Google Scholar
Google Scholar
Liu S, Wei Y P, Liu J Y, Zhang G P 2020 J. Cent. Chin. Normal Univ. (Nat. Sci.) 54 36
 Google Scholar
Google Scholar
[8] 庄志本, 李军, 刘静漪, 陈世强 2020 69 50
 Google Scholar
Google Scholar
Zhuang Z B, Li J, Liu J Y, Chen S Q 2020 Acta Phys. Sin. 69 50
 Google Scholar
Google Scholar
[9] 吴庆庆, 郑雅婷, 李涛 2014 中国科技论文 9 130
 Google Scholar
Google Scholar
Wu Q Q, Zheng Y T, Li T 2014 Science Paper Online 9 130
 Google Scholar
Google Scholar
[10] 颜闽秀, 林建峰, 谢俊红 2021 南京邮电大学学报(自然科学版) 41 66
Yan M X, Lin J F, Xie J H 2021 J. Nanjing Youdian Univ. (Nat. Sci.) 41 66
[11] Chua L O 1971 IEEE Trans. Circuits Theor. 18 507
 Google Scholar
Google Scholar
[12] Strukov D B, Snider G S, Stewart D R, Stanley W R 2008 Nature 453 80
 Google Scholar
Google Scholar
[13] Wang M J, Deng Y, Liao X H, Li Z J, Ma M L, Zeng Y C 2019 Int. J. Nonlin. Mech. 111 149
 Google Scholar
Google Scholar
[14] 徐昌彪, 何颖辉, 吴霞, 莫运辉 2020 哈尔滨工业大学学报 52 92
 Google Scholar
Google Scholar
Xu C B, He Y H, Wu X, Mo Y H 2020 J. Harbin Eng. Univ. 52 92
 Google Scholar
Google Scholar
[15] Hu H Y, Cao Y H, Hao J, Li X J, Mou J 2022 Multimed. Tools Appl. 82 4343
 Google Scholar
Google Scholar
[16] Guo Z G, Wen J J, Mou J 2022 Mathematics 11 1
[17] 鲜永菊, 莫运辉, 徐昌彪, 吴霞, 何颖辉 2020 华南理工大学学报(自然科学版) 48 32
 Google Scholar
Google Scholar
Xian Y J, Mo Y H, Xu C B, Wu X, He Y H 2020 J. Huanan Ligong Univ. (Nat. Sci.) 48 32
 Google Scholar
Google Scholar
[18] 王徐盱, 张宏昊, 赖强 2021 电子元件与材料 40 1208
 Google Scholar
Google Scholar
Wang X X, Zhang H H, Lai Q 2021 Electron. Components Mater. 40 1208
 Google Scholar
Google Scholar
[19] 鲜永菊, 扶坤荣, 徐昌彪 2021 振动与冲击 40 15
 Google Scholar
Google Scholar
Xian Y J, Fu K R, Xu C B 2021 J. Vibr. Shock 40 15
 Google Scholar
Google Scholar
[20] 李木子, 许荣今, 岳立娟 2021 东北师大学报(自然科学版) 53 120
 Google Scholar
Google Scholar
Li M Z, Xu R J, Yue L J 2021 J. Dongbei Shida Univ. (Nat. Sci.) 53 120
 Google Scholar
Google Scholar
[21] 闵富红, 王珠林, 曹戈, 王恩荣 2018 电子学报 46 9
 Google Scholar
Google Scholar
Min F H, Wang Z L, Cao G, Wang E R 2018 Acta Electronica Sin. 46 9
 Google Scholar
Google Scholar
[22] Ma X J, Mou J, Li X, Banerjee S, Cao Y H, Wang J Y 2021 Chaos Solit. Frac. 152 111363
 Google Scholar
Google Scholar
[23] Bao H, Wang N, Bao B C, Chen M, Jin P P, Wang G Y 2018 Commun. Nonlinear Sci. 57 264
 Google Scholar
Google Scholar
[24] Yu F, Liu L, Qian S, Li L X, Huang Y Y, Shi C Q, Cai S, Wu X M, Du S C, Wan Q Z 2020 Complexity 2020 1
 Google Scholar
Google Scholar
[25] 李晓霞, 郑驰, 王雪, 曹樱子, 徐桂芝 2022 哈尔滨工业大学学报 69 163
 Google Scholar
Google Scholar
Li X X, Zheng C, Wang X, Cao Y Z, Xu G Z 2022 J. Harbin Eng. Univ. 69 163
 Google Scholar
Google Scholar
[26] 秦铭宏, 赖强, 吴永红 2022 71 160502
 Google Scholar
Google Scholar
Qin M H, Lai Q, Wu Y H 2022 Acta Phys. Sin. 71 160502
 Google Scholar
Google Scholar
[27] Li Q D, Zeng H Z, Li J 2015 Nonlinear Dyn. 79 2295
 Google Scholar
Google Scholar
[28] Yang Q G, Wei Z C, Chen G R 2010 Int. J. Bifur. Chao 20 1061
 Google Scholar
Google Scholar
[29] 孙克辉, 汪艳, 刘璇 2013 电路与系统学报 18 500
 Google Scholar
Google Scholar
Sun K H, Wang Y, Liu X 2013 J. Circuits Syst. 18 500
 Google Scholar
Google Scholar
[30] 陈志盛, 孙克辉, 张泰山 2005 6 2580
 Google Scholar
Google Scholar
Chen Z S, Sun K H, Zhang T S 2005 Acta Phys. Sin. 6 2580
 Google Scholar
Google Scholar
[31] 付景超, 张中华 2016 控制与决策 31 1707
 Google Scholar
Google Scholar
Fu J C, Zhang Z H 2016 Control Decision 31 1707
 Google Scholar
Google Scholar
[32] 毛北行, 王东晓, 卜春霞 2012 华中师范大学学报(自然科学版) 46 297
 Google Scholar
Google Scholar
Mao B X, Wang D X, Bu C X 2012 J. Cent. Chin. Normal Univ. (Nat. Sci.) 46 297
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 5560
- PDF Downloads: 157
- Cited By: 0














 DownLoad:
DownLoad: