Quantitative study on isotope effect of rubidium clusters

Di Shu-Hong; Zhang Yang; Yang Hui-Jing; Cui Nai-Zhong; Li Yan-Kun; Liu Hui-Yuan; Li Ling-Li; Shi Feng-Liang; Jia Yu-Xuan

doi:10.7498/aps.72.20230778

Abstract

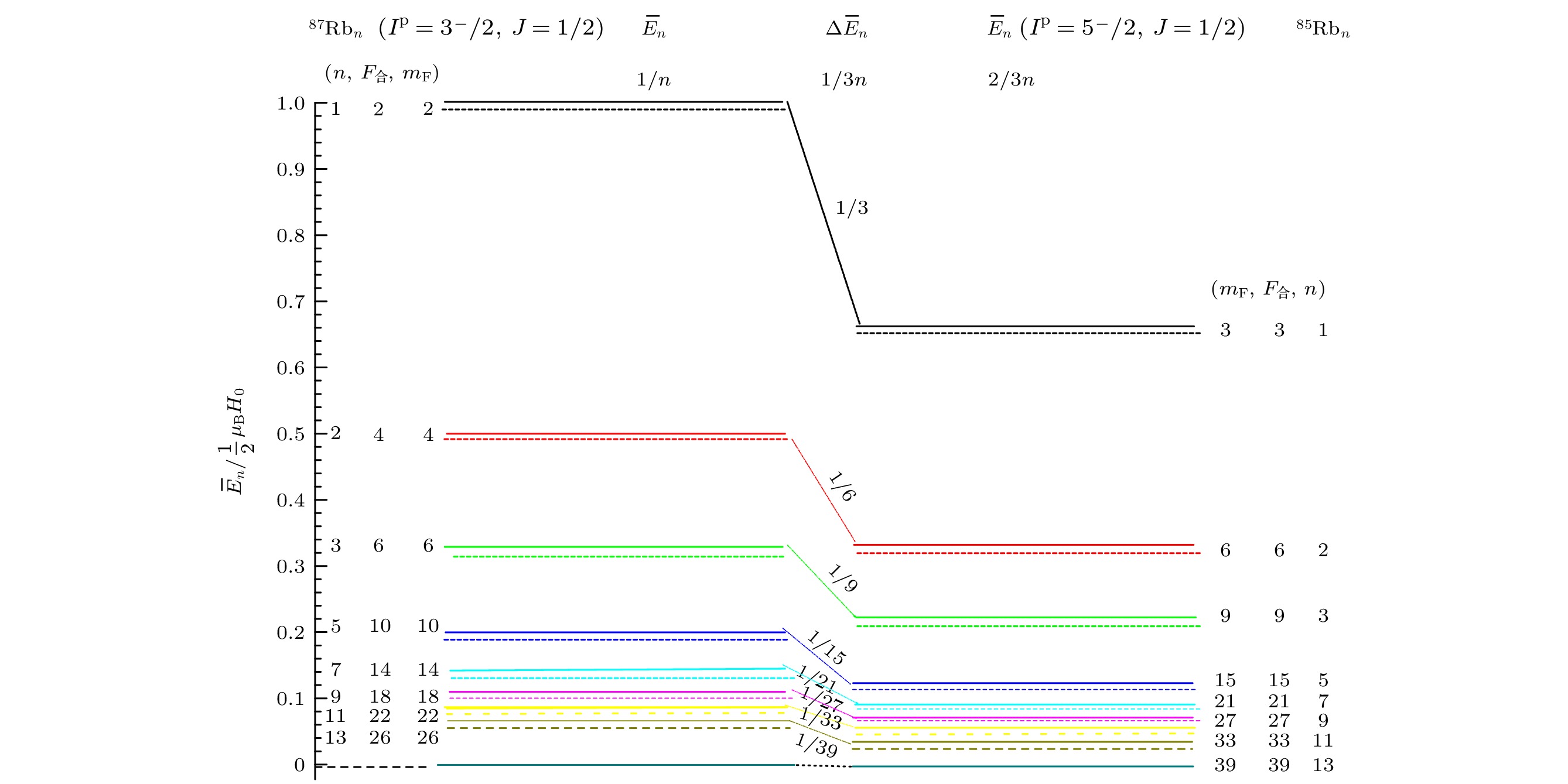
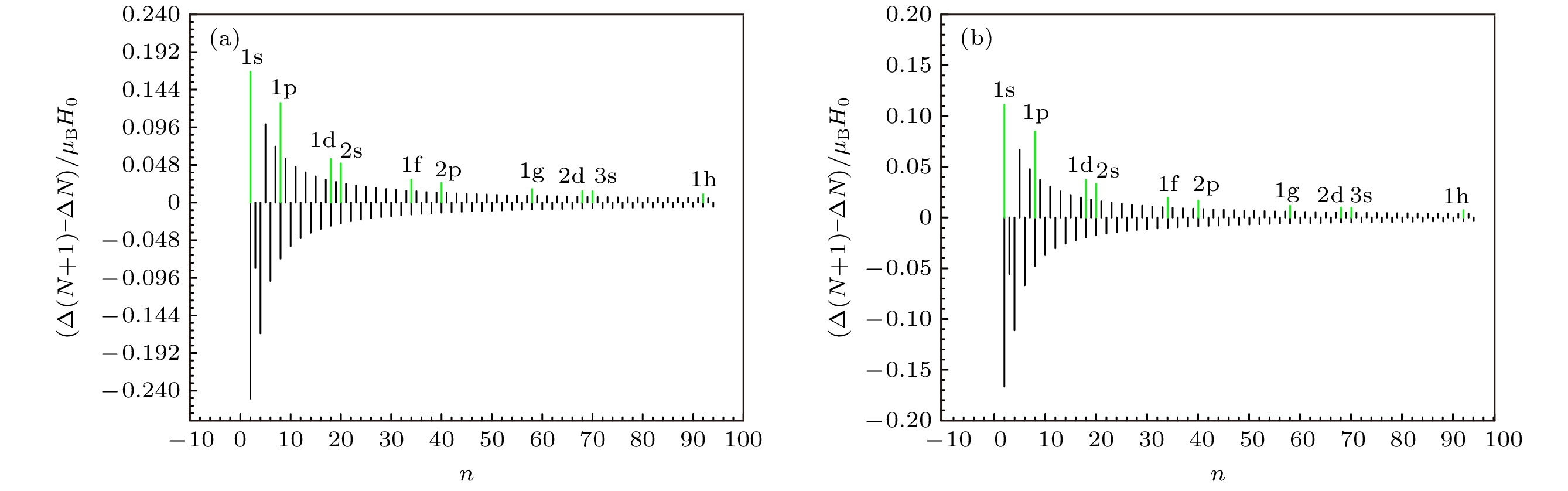
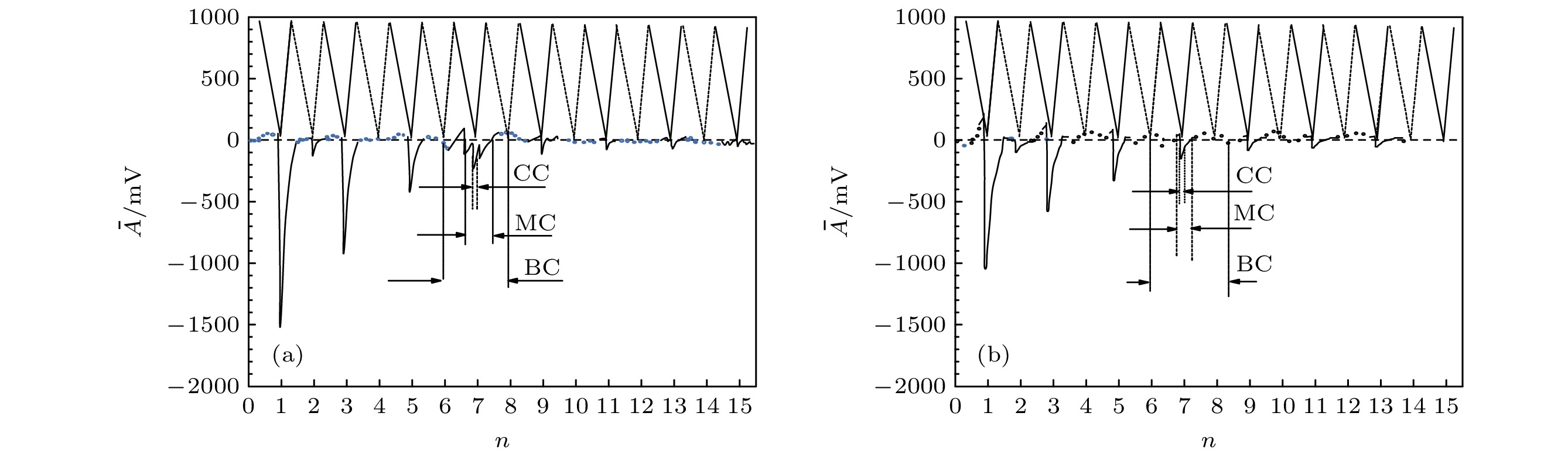
Because of the difficulty in measuring the cluster isotope displacement and identifying its cause, the resonance dissociation spectra, the moment shift and Zeeman energy shift of isotope cluster ^87,85Rb_n (n = 1, 2, 3, ··· , 13) are obtained by the combination of optical magnetic resonance and thermal dissociation techniques in this study. The quantitative calculation is carried out based on the conceptual model of the giant atom, and the results are in excellent agreement with the measured results, which shows that rubidium clusters can be analyzed as giant atoms. Furthermore, 5s electron shell level structures of the rubidium cluster ^87,85Rb_n (n = 1, 2, 3, ··· , 92) are calculated by using Zeeman level interval model. It is found that the main order and step distance of the 5s electron shell structure are similar to those of 3s single electron shell structure of sodium cluster in spherical symmetry. It is confirmed that the structure of the 5s electron shell of the rubidium cluster is determined by the largest energy gap in total Zeeman levels and the characteristic peaks of odd and even alternating and anomalous magnetic moments of special numbers such as n = 2 are caused by the intrinsic properties of electrons and molecular structures. It is also found that ⁸⁷Rb_n level shell structure and ⁸⁵Rb_n level shell structure strictly conform to the ratio of 3/2 magnitude relationship, and that there are abnormal differences in spectral center frequency and broadening, which may be directly related to the ^85,87Rb nuclei close to the shell closure.

Keywords:

Authors and contacts

1.
Institute of Physics Science & Technology, Tangshan Normal University, Tangshan 063000, China
2.
State Key Laboratory of Disastrous Weather, Chinese Academy of Meteorological Sciences, Beijing 100081, China
3.
Department of Chemistry, Tangshan Normal University, Tangshan 063000, China

Corresponding author: Di Shu-Hong, zhudizhe@163.com ; Zhang Yang, 185540891@qq.com ; Yang Hui-Jing, yanghj619@126.com ;

FullText HTML : translate this paragraph

Supplements

2023年72卷182101-补充材料.ZIP

References

[1]	Makarov V I, Kochubei S A, Khmelinskii I V 2003 Chem. Phys. Lett. 376 230 Google Scholar
[2]	DE Bievre P J, Debus G H 1965 Nucl. Instrum. Meth. 32 224 Google Scholar
[3]	Bokhan P A, Buchanov V V, Zakrevskii D E, Kazaryan M A, Kalugin M M, Fateev N V 2003 J. Russ. Laser Res. 24 159
[4]	Macadam K B, Steibach A, Wieman C 1992 Am. J. Phys. 60 1098 Google Scholar
[5]	Patrick H, Wieman C E 1991 Rev. Sci. Instrum. 62 2593 Google Scholar
[6]	Lapitajs G, Hendrickx 1 F, Verbruggen A, Lamberty A 1996 Int. J. Mass. Spectyom. Ion. Proc. 152 69 Google Scholar
[7]	Minster J F, Allegre C J 1976 Earth. Planet. Sc. Lett. 32 191 Google Scholar
[8]	De Bievre P 1990 Fresen. J. Anal. Chem. 337 766 Google Scholar
[9]	Waight T, Baker J, Willigers B 2002 Chem. Geol. 186 99 Google Scholar
[10]	Nebel O, Mezger K, Scherer E E, Munker C 2005 Int. J. Mass. Spectrom. 246 10 Google Scholar
[11]	Knight W D, Clemenger K, Walt A, Heer D, Saunders W A, Chou M Y, Cohen M L 1984 Phys. Rev. Lett. 52 2141 Google Scholar
[12]	Saito S, Ohnishi S 1987 Physics and Chemistry of Small Clusters (New York: New York and London Published in Cooperation with NATO Scientific Affairs Division Plenum Press) p115
[13]	Nozue Y, Kodaira T, Ohwashi S, Togashi N, Terasaki O 1996 Surf. Rev. Lett. 3 701 Google Scholar
[14]	Igarashi M, Kodaira T, Ikeda T, Itoh M, Shimizu T, Goto A , Nozue Y 2003 Physics B 327 72
[15]	邸淑红, 张阳, 杨会静, 伞星原, 刘会媛, 张素恒, 李繁麟, 太军君, 周春丽 2021 70 122101 Google Scholar Di S H, Zhang Y, Yang H J, San X Y, Liu H Y, Zhang S H, Li F L, Tai J J, Zhou C L 2021 Acta Phys. Sin. 70 122101 Google Scholar
[16]	吴思成, 王祖铨1999近代物理实验 (北京: 北京大学出版社) 第348—358页 Wu S C, Wang Z Q 1999 Modern Physics Experiment (Beijing: BeijingUniversity Press) pp348–358
[17]	格哈德 H (王鼎昌译) 1983 分子光谱与分子结构(第1卷) (北京: 科学出版社) 第1—272页 Gerhard H (translated by Wang D C)1983 Molecules Spectroscopy and Molecules Structures (Vol. 1) (Beijing: Science Press) pp1–272
[18]	周公度, 叶宪曾2012化学元素综论 (北京: 科学出版社) 第366页 Zhou G D, Ye X Z 2012 Chemical Elements Survey (Beijing: Science Press) p366
[19]	Jahn H A, Teller E 1937 Proc. Roy. Soc. A 161 220
[20]	Jahn H A 1938 Proc. Roy. Soc. A 164 117
[21]	Kubo R 1962 J. Phys. Soc. Jpn. 17 975 Google Scholar
[22]	关洪 2000 量子力学基础 (北京: 高等教育出版社) 第168—174页 Guan H 2000 Basic Quantum Mechanics (Beijing: Higher Education Press) pp168–174
[23]	Ekstrom C, Ingelman S, Wannberg G, Skarestad M, 1978 Nucl. Phys. A 311 269 Google Scholar

Cited By

图 1 (a), (b)实验测得的⁸⁷Rb_n, ⁸⁵Rb_n的8种簇粒子的共振频率$ \bar f $与磁场H₀的关系曲线(1 G = 10^–4 T)

Figure 1. (a), (b) Relationship between the resonant frequency $ \bar f $ of 8 kinds of ⁸⁷Rb_n, ⁸⁵Rb_n cluster particles and the magnetic field H₀

DownLoad: Full-Size Img PowerPoint

图 2 (a), (b) 两系列同位素原子簇的⁸⁷Rb_n, ⁸⁵Rb_n(n = 1, 2, ···, 13)的共振离解光谱

Figure 2. (a), (b) Resonance dissociation spectra of two series of isotopic atomic clusters ⁸⁷Rb_n, ⁸⁵Rb_n (n = 1, 2, ···, 13).

DownLoad: Full-Size Img PowerPoint

图 3 等数簇矩移随n变化的模型值与实验值比较图(实验值用虚线, 模型值用实线)

Figure 3. Comparison of calculated values and experimental values of magnetic moment shift of equal number cluster with n (dashed lines for experimental value, full lines for model value).

DownLoad: Full-Size Img PowerPoint

图 4 等数簇超精细结构塞曼能移随n变化的模型值与实验值比较图(实验值用虚线, 模型值用实线)

Figure 4. Comparison of calculated values and experimental values of Zeeman energy shift of equal-number hyperfine structures with n (dashed lines for experimental value, full lines for model value).

DownLoad: Full-Size Img PowerPoint

图 5 (a)⁸⁷Rb_n 5s电子壳层能级结构; (b) ⁸⁵Rb_n5s电子壳层能级结构

Figure 5. 　(a) 5s electron shell level structure of ⁸⁷Rb_n; (b) 5s electron shell level structure of ⁸⁵Rb_n.

DownLoad: Full-Size Img PowerPoint

图 6 (a), (b) ⁸⁷Rb_n, ⁸⁵Rb_n同位素原子簇的相对频移图

Figure 6. (a), (b) Diagrams of relative frequency shift of equal-number cluster ⁸⁷Rb_n, ⁸⁵Rb_n.

DownLoad: Full-Size Img PowerPoint

表 1 实验测量的⁸⁷Rb_n, ⁸⁵Rb_n等数簇平均矩移和塞曼能移及光谱振幅

Table 1. Measured mean magnetic moment shifts, Zeeman energy shifts and spectrum amplitudes of ⁸⁷Rb_n, ⁸⁵Rb_n.

^87,85Rb_n	5s 电子数	磁矩及矩移/μ_B			塞曼能移 $ \Delta {\bar E_n}/{\mu _{\text{B}}}{H_0} $	磁矩比 $ {\bar \mu _{{87}n}}/{\bar \mu _{{85}n}} $	塞曼能比 $ {\bar E_{87 n}}/{\bar E_{85 n}} $	光谱平均幅度/mV
^87,85Rb_n	5s 电子数	$ {\bar \mu _{87 n}} $	$ {\bar \mu _{85 n}} $	$ \Delta {\bar \mu _n} $	塞曼能移 $ \Delta {\bar E_n}/{\mu _{\text{B}}}{H_0} $	磁矩比 $ {\bar \mu _{{87}n}}/{\bar \mu _{{85}n}} $	塞曼能比 $ {\bar E_{87 n}}/{\bar E_{85 n}} $	${{{{\bar A}_{87n}}}} $	${{{{\bar A}_{85n}}}} $	${{{{\bar A}_{87n}}}}/ {{{{\bar A}_{85n}}}} $
^87,85Rb₁	1	0.494337	0.330120	0.164217	0.164217	1.497446	1.497446	1574.50	1008.71	1.56∶1
^87,85Rb₂	2	0.246984	0.164773	0.082211	0.082211	1.498935	1.498935	105.75	70.60	1.50∶1
^87,85Rb₃	3	0.164598	0.109974	0.054624	0.054624	1.496699	1.496699	883.07	589.49	1.49∶1
^87,85Rb₄	4	0	0	0	0			0	0	无共振
^87,85Rb₅	5	0.098789	0.066044	0.032745	0.032745	1.495805	1.495805	383.47	354.10	1.08∶1
^87,85Rb₆	6	0	0	0	0			0	0	无共振
^87,85Rb₇	7	0.070635	0.047180	0.023455	0.023455	1.497139	1.497139	188.70	170.63	1.10∶1
^87,85Rb₈	8	0	0	0	0			0	0	无共振
^87,85Rb₉	9	0.054953	0.036718	0.018235	0.018235	1.496623	1.496623	84.92	79.59	1.06∶1
^87,85Rb₁₀	10	0	0	0	0			0	0	无共振
^87,85Rb₁₁	11	0.044975	0.030046	0.014929	0.014929	1.496871	1.496871	48.62	39.90	1.18∶1
^87,85Rb₁₂	12	0	0	0	0			0	0	无共振
^87,85Rb₁₃	13	0.038060	0.025423	0.012637	0.012637	1.497070	1.497070	31.55	23.07	1.34∶1

DownLoad: CSV

表 2 ⁸⁷Rb_n, ⁸⁵Rb_n双原子分子基态X和最低激发态A的电子组态和分子态项型表

Table 2. Electronic configuration and molecular state item type of 8 pairs of diatomic molecule ⁸⁷Rb_n , ⁸⁵Rb_n ground and lowest excited states.

团簇分子, 参考分子	X组态和分子态及其$ {\lambda }_{合} $和s	A组态和分子态及其$ {\lambda }_{合} $和s	X与A 稳定性比较$ {p_{\text{a}}} - {p_{\text{b}}}$
^87,85Rb₁	$ \begin{array}{c}{\text{KLMNspd(σ}}_{\text{g}}\text{5s}), \\ {}^{2}\text{Σ}{}_{\text{g}}^{+}, {\lambda }_{合}=0, s=1/2\end{array} $	$ \begin{array}{c} \text{KLMNspd}({\text{π}}_{\text{u}}4\text{d}), \\ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1/2; \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1/2 \end{array} $
^87,85Rb₂^[17]	$ \begin{array}{c}({\text{σ}}_{\text{g}}\text{5s})^{2}, {}^{1}\Sigma {}_{\text{g}}^{+}, {\lambda }_{合}=0, s=\text{0;}\\({\text{σ}}_{\text{g}}\text{5s)}{\text{(σ}}_{\text{u}}\text{5s)}, {}^{3}\Sigma {}_{\rm u}^{+}, \\{\lambda }_{合}=0, s=1\end{array} $	$ \begin{array}{c}{\text{(σ}}_{\text{g}}{\text{5s)(π}}_{\text{u}}\text{4d)}, {}^{1}\Pi_{\text{u}}, {\lambda }_{合}=1, s=0;\\或\; ({\text{σ}}_{\text{u}}{\text{5s)(π}}_{\text{u}}\text{4d)}, {}^{3}\Pi_{\text{g}},\\ {\lambda }_{合}=1, s=1\end{array} $	$ \begin{array}{l} {}\quad\;{\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1 - 0 = 1; \\ {}\quad\;{\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1 - 0 = 1 \\ 或\; {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1/2 - 1/2 = 0; \\ {}\quad\;{\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1/2 - 1/2 = 0\, \end{array} $
^87,85Rb₃	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{\text{(σ}}_{\text{u}}\text{5s)}, \\ {}^{2}\Sigma_{\text{u}}^{+}, {\lambda}_{合}=0, s=1/2\end{array} $	$ \begin{array}{c}{\text{(σ}}_{\text{g}}\text{5s)}{\text{(σ}}_{\text{u}}\text{5s)}{\text{(π}}_{\text{u}}\text{4d), }\\ {}^{2}\Pi_{\text{g}}^{}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1 - 1/2 = 1/2 \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1 - 1/2 = 1/2 \end{array} $
^87,85Rb₅	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{\text{(σ}}_{\text{g}}\text{4d), }\\ {}^{2}\Sigma_{\text{g}}^{+}, {\lambda }_{合}=0, s=1/2\end{array} $	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{\text{(π}}_{\text{u}}\text{4d)}, \\ {}^{2}\Pi_{\text{u}}^{}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1\dfrac{1}{2} - 1 = 1/2 \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 1\dfrac{1}{2} - 1 = 1/2 \end{array} $
^87,85Rb₇	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{{\text{(σ}}_{\text{g}}}{\text{4d)}}^2{\text{(π}}_{\text{u}}\text{4d)}, \\ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{{\text{(σ}}_{\text{g}}}{\text{4d)}}^1{{\text{(π}}_{\text{u}}}{\text{4d)}}^2, \\{}^{2}\Sigma_{\text{g}}^{+}, {\lambda }_{合}=0, s=1/2;\\ {}^{2}\Delta_{\text{g}}, {\lambda }_{合}=2, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 2\dfrac{1}{2} - 1 = 1\dfrac{1}{2} \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 2\dfrac{1}{2} - 1 = 1\dfrac{1}{2} \end{array} $
^87,85Rb₉	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{{\text{(σ}}_{\text{g}}}{\text{4d)}}^2{{\text{(π}}_{\text{u}}}{\text{4d)}}^3, \\ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{{\text{(σ}}_{\text{g}}}{\text{4d)}}^1{{\text{(π}}_{\text{u}}}{\text{4d)}}^4, \\ {}^{2}\Sigma_{\text{g}}^{+}, {\lambda }_{合}=0, s=1/2;\\ {}^{2}\Delta_{\text{g}}, {\lambda }_{合}=2, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 3\dfrac{1}{2} - 1 = 2\dfrac{1}{2} \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 3\dfrac{1}{2} - 1 = 2\dfrac{1}{2} \end{array} $
^87,85Rb₁₁	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{{\text{(σ}}_{\text{g}}}{\text{4d)}}^2{{\text{(π}}_{\text{u}}}{\text{4d)}}^4{{\text{(π}}_{\text{g}}}{\text{4d)}}^1, \\ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^1{{\text{(σ}}_{\text{g}}}{\text{4d)}}^2{{\text{(π}}_{\text{u}}}{\text{4d)}}^4{{\text{(π}}_{\text{g}}}{\text{4d)}}^2, \\ {}^{2}\Sigma_{\text{g}}^{+}, {\lambda }_{合}=0, s=1/2;\\ {}^{2}\Delta_{\text{g}}, {\lambda }_{合}=2, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 4 - 1\dfrac{1}{2} = 2\dfrac{1}{2} \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 4 - 1\dfrac{1}{2} = 2\dfrac{1}{2} \end{array} $
^87,85Rb₁₃	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^2{{\text{(σ}}_{\text{g}}}{\text{4d)}}^2{{\text{(π}}_{\text{u}}}{\text{4d)}}^4{{\text{(π}}_{\text{g}}}{\text{4d)}}^3, \\ {}^{2}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1/2\end{array} $	$ \begin{array}{c}{{\text{(σ}}_{\text{g}}}{\text{5s)}}^2{{\text{(σ}}_{\text{u}}}{\text{5s)}}^1{{\text{(σ}}_{\text{g}}}{\text{4d)}}^2{{\text{(π}}_{\text{u}}}{\text{4d)}}^4{{\text{(π}}_{\text{g}}}{\text{4d)}}^4, \\ {}^{2}\Sigma_{\text{u}}, {\lambda }_{合}=0, s=1/2\end{array} $	$ \begin{array}{c} {\text{X:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 4 - 2\dfrac{1}{2} = 1\dfrac{1}{2} \\ {\text{A:}}\, {p_{\text{a}}} - {p_{\text{b}}} = 4 - 2\dfrac{1}{2} = 1\dfrac{1}{2} \end{array} $
注: 表2中电子组态仅^87,85Rb₁的基态和激发态标出了闭壳层KLMNspd, 其他粒子没有重复标出闭壳层KLMNspd.

DownLoad: CSV

表 3 原子簇⁸⁷Rb_n磁矩和塞曼能级间隔模型与实验结果比较

Table 3. Comparison of experiment values and calculated values of magnetic moment and Zeeman energy level interval of ⁸⁷Rb_n atomic cluster.

⁸⁷Rb_n	5s 电子数	分子态及本征值$ {\lambda }_{合} $和s	模型 F_合	$ {\bar \mu _n}/{\mu _{\text{B}}} $		$ {\bar \mu _n} $相对误差/‰	$ {\bar E_n}/{\mu _{\text{B}}}{H_0} $		$ {\bar E_n} $相对误差/‰
⁸⁷Rb_n	5s 电子数	分子态及本征值$ {\lambda }_{合} $和s	模型 F_合	模型	实验	$ {\bar \mu _n} $相对误差/‰	模型	实验	$ {\bar E_n} $相对误差/‰
⁸⁷Rb₁	1	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	2	$ 1/2 $	0.494337	–11.326	$ 1/2 $	0.494337	–11.326
⁸⁷Rb₂	2	$ {}^{3}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1 $	4	$ 1/4 $	0.246984	–12.064	$ 1/4 $	0.246984	–12.064
⁸⁷Rb₃	3	$ {}^{2}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1/2 $	6	$ 1/6 $	0.164598	–12.412	$ 1/6 $	0.164598	–12.412
⁸⁷Rb₅	5	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	10	$ 1/10 $	0.098789	–12.110	$ 1/10 $	0.098789	–12.110
⁸⁷Rb₇	7	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	14	$ 1/14 $	0.070635	–11.110	$ 1/14 $	0.070635	–11.110
⁸⁷Rb₉	9	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	18	$ 1/18 $	0.054953	–10.846	$ 1/18 $	0.054953	–10.846
⁸⁷Rb₁₁	11	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	22	$ 1/22 $	0.044975	–10.550	$ 1/22 $	0.044975	–10.550
⁸⁷Rb₁₃	13	$ {}^{2}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1/2 $	26	$ 1/26 $	0.038060	–10.440	$ 1/26 $	0.038060	–10.440
⁸⁷Rb_4,6,8,10,12	4, 6, 8, 10, 12	[19, 20, 21]		0	0	0	0	0	0
平均值						–6.989			–6.989

DownLoad: CSV

表 4 ⁸⁵Rb_n磁矩和塞曼能级间隔模型与实验结果比较

Table 4. Comparison of experiment values and calculated values of magnetic moment and Zeeman energy level interval of ⁸⁵Rb_n atomic cluster.

⁸⁵Rb_n	5s 电子数	分子态及本征值$ {\lambda }_{合} $和s	模型 F_合	$ {\bar \mu _n}/{\mu _{\text{B}}} $		$ {\bar \mu _n} $相对误差/‰	$ {\bar E_n}/{\mu _{\text{B}}}{H_0} $		$ {\bar E_n} $相对误差/‰
⁸⁵Rb_n	5s 电子数	分子态及本征值$ {\lambda }_{合} $和s	模型 F_合	模型	实验	$ {\bar \mu _n} $相对误差/‰	模型	实验	$ {\bar E_n} $相对误差/‰
⁸⁵Rb₁	1	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	3	1/3	0.330120	–9.640	1/3	0.330120	–9.640
⁸⁵Rb₂	2	$ {}^{3}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1 $	6	1/6	0.164773	–11.362	1/6	0.164773	–11.362
⁸⁵Rb₃	3	$ {}^{2}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1/2 $	9	1/9	0.109974	–10.234	1/9	0.109974	–10.234
⁸⁵Rb₅	5	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	15	1/15	0.066044	–9.340	1/15	0.066044	–9.340
⁸⁵Rb₇	7	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	21	1/21	0.047180	–9.220	1/21	0.047180	–9.220
⁸⁵Rb₉	9	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	27	1/27	0.036718	–8.614	1/27	0.036718	–8.614
⁸⁵Rb₁₁	11	$ {}^{2}\Pi_{\text{u}}, {\lambda }_{合}=1, s=1/2 $	33	1/33	0.030046	–8.482	1/33	0.030046	–8.482
⁸⁵Rb₁₃	13	$ {}^{2}\Pi_{\text{g}}, {\lambda }_{合}=1, s=1/2 $	39	1/39	0.025423	–8.503	1/39	0.025423	–8.503
⁸⁵Rb_4,6,8,10,12	4, 6, 8, 10, 12	[19, 20, 21]		0	0	0	0	0	0
平均值						–5.800			–5.800

DownLoad: CSV

表 5 ⁸⁷Rb_n和⁸⁵Rb_n等数簇矩移模型与实验结果对比

Table 5. Comparison of experiment values and calculated values of magnetic moment shift interval of ⁸⁷Rb_n and ⁸⁵Rb_n.

n	$ {\bar \mu _n}/{\mu _{\text{B}}} $		模型矩移 $ \Delta {\bar \mu _n}/{\mu _{\text{B}}} $	$ {\bar \mu _n}/{\mu _{\text{B}}} $		实验矩移 $ \Delta {\bar \mu _n}/{\mu _{\text{B}}} $	相对误差/‰
n	⁸⁷Rb_n 模型	⁸⁵Rb_n 模型	模型矩移 $ \Delta {\bar \mu _n}/{\mu _{\text{B}}} $	⁸⁷Rb_n 实验	⁸⁵Rb_n 实验	实验矩移 $ \Delta {\bar \mu _n}/{\mu _{\text{B}}} $	相对误差/‰
1	1/2	1/3	1/6	0.494337	0.330120	0.164217	–14.698
2	1/4	1/6	1/12	0.246984	0.164773	0.082211	–13.468
3	1/6	1/9	1/18	0.164598	0.109974	0.054624	–16.768
4	0	0	0	0	0	0	0
5	1/10	1/15	1/30	0.098789	0.066044	0.032745	–17.65
6	0	0	0	0	0	0	0
7	1/14	1/21	1/42	0.070635	0.047180	0.023455	–14.89
8	0	0	0	0	0	0	0
9	1/18	1/27	1/54	0.054953	0.036718	0.018235	–15.31
10	0	0	0	0	0	0	0
11	1/22	1/33	1/66	0.044975	0.030046	0.014929	–14.686
12	0	0	0	0	0	0	0
13	1/26	1/39	1/78	0.038060	0.025423	0.012637	–14.314
平均值							–9.368

DownLoad: CSV

表 6 ⁸⁷Rb_n和⁸⁵Rb_n等数簇塞曼能移实验与模型结果比较

Table 6. Comparison of experiment values and calculated values of Zeeman energy level shiift interval of ⁸⁷Rb_n and ⁸⁵Rb_n.

n	$ {\bar E_n}/{\mu _{\text{B}}}{H_0} $		模型能移 $\Delta {\bar E_n}/{\mu _{\text{B}}}{H_0} $	$ {\bar E_n}/{\mu _{\text{B}}}{H_0} $		实验能移 $ \Delta{\bar E_n}/{\mu _{\text{B}}}{H_0} $	相对误差/‰
n	⁸⁷Rb_n 模型	⁸⁵Rb_n 模型	模型能移 $\Delta {\bar E_n}/{\mu _{\text{B}}}{H_0} $	⁸⁷Rb_n 实验	⁸⁵Rb_n 实验	实验能移 $ \Delta{\bar E_n}/{\mu _{\text{B}}}{H_0} $	相对误差/‰
1	1/2	1/3	1/6	0.494337	0.330120	0.164217	–14.698
2	1/4	1/6	1/12	0.246984	0.164773	0.082211	–13.468
3	1/6	1/9	1/18	0.164598	0.109974	0.054624	–16.768
4	0	0	0	0	0	0	0
5	1/10	1/15	1/30	0.098789	0.066044	0.032745	–17.65
6	0	0	0	0	0	0	0
7	1/14	1/21	1/42	0.070635	0.047180	0.023455	–14.89
8	0	0	0	0	0	0	0
9	1/18	1/27	1/54	0.054953	0.036718	0.018235	–15.31
10	0	0	0	0	0	0	0
11	1/22	1/33	1/66	0.044975	0.030046	0.014929	–14.686
12	0	0	0	0	0	0	0
13	1/26	1/39	1/78	0.038060	0.025423	0.012637	–14.314
平均值							–9.368

DownLoad: CSV

表 7 实验测量 ⁸⁷Rb_n, ⁸⁵Rb_n 光谱中心频率宽度与广泛成分平均宽度BC

Table 7. Spectral center frequency width CC and average width BC of ⁸⁷Rb_n, ⁸⁵Rb_n measured by experiments.

n	1	5	7	9
1/2 CC₈₇/kHz	78.52	19.22	7.92	8.73
1/2 CC₈₅/kHz	98.34	24.84	17.06	12.41
CC₈₇/CC₈₅	0.80	0.77	0.46	0.70
BC₈₇/kHz	812.75	167.60	116.40	89.10
BC₈₅/kHz	510.55	113.51	74.35	58.63
BC₈₇/BC₈₅	1.59	1.47	1.57	1.48
注: 实验测量的1/2 CC是共振峰的半峰高处左半部分对应的中心频率的展宽.

DownLoad: CSV

map

[1]	Makarov V I, Kochubei S A, Khmelinskii I V 2003 Chem. Phys. Lett. 376 230 Google Scholar
[2]	DE Bievre P J, Debus G H 1965 Nucl. Instrum. Meth. 32 224 Google Scholar
[3]	Bokhan P A, Buchanov V V, Zakrevskii D E, Kazaryan M A, Kalugin M M, Fateev N V 2003 J. Russ. Laser Res. 24 159
[4]	Macadam K B, Steibach A, Wieman C 1992 Am. J. Phys. 60 1098 Google Scholar
[5]	Patrick H, Wieman C E 1991 Rev. Sci. Instrum. 62 2593 Google Scholar
[6]	Lapitajs G, Hendrickx 1 F, Verbruggen A, Lamberty A 1996 Int. J. Mass. Spectyom. Ion. Proc. 152 69 Google Scholar
[7]	Minster J F, Allegre C J 1976 Earth. Planet. Sc. Lett. 32 191 Google Scholar
[8]	De Bievre P 1990 Fresen. J. Anal. Chem. 337 766 Google Scholar
[9]	Waight T, Baker J, Willigers B 2002 Chem. Geol. 186 99 Google Scholar
[10]	Nebel O, Mezger K, Scherer E E, Munker C 2005 Int. J. Mass. Spectrom. 246 10 Google Scholar
[11]	Knight W D, Clemenger K, Walt A, Heer D, Saunders W A, Chou M Y, Cohen M L 1984 Phys. Rev. Lett. 52 2141 Google Scholar
[12]	Saito S, Ohnishi S 1987 Physics and Chemistry of Small Clusters (New York: New York and London Published in Cooperation with NATO Scientific Affairs Division Plenum Press) p115
[13]	Nozue Y, Kodaira T, Ohwashi S, Togashi N, Terasaki O 1996 Surf. Rev. Lett. 3 701 Google Scholar
[14]	Igarashi M, Kodaira T, Ikeda T, Itoh M, Shimizu T, Goto A , Nozue Y 2003 Physics B 327 72
[15]	邸淑红, 张阳, 杨会静, 伞星原, 刘会媛, 张素恒, 李繁麟, 太军君, 周春丽 2021 70 122101 Google Scholar Di S H, Zhang Y, Yang H J, San X Y, Liu H Y, Zhang S H, Li F L, Tai J J, Zhou C L 2021 Acta Phys. Sin. 70 122101 Google Scholar
[16]	吴思成, 王祖铨1999近代物理实验 (北京: 北京大学出版社) 第348—358页 Wu S C, Wang Z Q 1999 Modern Physics Experiment (Beijing: BeijingUniversity Press) pp348–358
[17]	格哈德 H (王鼎昌译) 1983 分子光谱与分子结构(第1卷) (北京: 科学出版社) 第1—272页 Gerhard H (translated by Wang D C)1983 Molecules Spectroscopy and Molecules Structures (Vol. 1) (Beijing: Science Press) pp1–272
[18]	周公度, 叶宪曾2012化学元素综论 (北京: 科学出版社) 第366页 Zhou G D, Ye X Z 2012 Chemical Elements Survey (Beijing: Science Press) p366
[19]	Jahn H A, Teller E 1937 Proc. Roy. Soc. A 161 220
[20]	Jahn H A 1938 Proc. Roy. Soc. A 164 117
[21]	Kubo R 1962 J. Phys. Soc. Jpn. 17 975 Google Scholar
[22]	关洪 2000 量子力学基础 (北京: 高等教育出版社) 第168—174页 Guan H 2000 Basic Quantum Mechanics (Beijing: Higher Education Press) pp168–174
[23]	Ekstrom C, Ingelman S, Wannberg G, Skarestad M, 1978 Nucl. Phys. A 311 269 Google Scholar

[1]	Liu Xuan, Gao Teng, Xie Shi-Jie. Isotope effect of carrier transport in organic semiconductors. Acta Physica Sinica, 2020, 69(24): 246701. doi: 10.7498/aps.69.20200789
[2]	Wu Yu, Cai Shao-Hong, Deng Ming-Sen, Sun Guang-Yu, Liu Wen-Jiang. First-principle study on quantum thermal transport in a polythiophene chain. Acta Physica Sinica, 2018, 67(2): 026501. doi: 10.7498/aps.67.20171198
[3]	Li Wen-Tao, Yu Wen-Tao, Yao Ming-Hai. H/D + Li2 LiH/LiD + Li reactions studied by quantum time-dependent wave packet approach. Acta Physica Sinica, 2018, 67(10): 103401. doi: 10.7498/aps.67.20180324
[4]	Shen Yong, Dong Jia-Qi, Xu Hong-Bing. Role of impurities in modifying isotope scaling law of ion temperature gradient turbulence driven transport in tokamak. Acta Physica Sinica, 2018, 67(19): 195203. doi: 10.7498/aps.67.20180703
[5]	Wu Yu, Cai Shao-Hong, Deng Ming-Sen, Sun Guang-Yu, Liu Wen-Jiang, Cen Chao. Isotope effect on quantum thermal transport in a polyethylene chain. Acta Physica Sinica, 2017, 66(11): 116501. doi: 10.7498/aps.66.116501
[6]	Wang Ming-Xin, Wang Mei-Shan, Yang Chuan-Lu, Liu Jia, Ma Xiao-Guang, Wang Li-Zhi. Influence of isotopic effect on the stereodynamics of reaction H+NH→N+H2. Acta Physica Sinica, 2015, 64(4): 043402. doi: 10.7498/aps.64.043402
[7]	Duan Zhi-Xin, Qiu Ming-Hui, Yao Cui-Xia. Quantum wave-packet and quasiclassical trajectory of reaction S(3P)+HD. Acta Physica Sinica, 2014, 63(6): 063402. doi: 10.7498/aps.63.063402
[8]	Wang Jie-Min, Zhang Lei, Shi De-Heng, Zhu Zun-Lue, Sun Jin-Feng. A Multi-reference configuration interaction investigation of the X2+and A2 low-lying electronic states of AsO+ isotope ion. Acta Physica Sinica, 2012, 61(15): 153105. doi: 10.7498/aps.61.153105
[9]	Sun Ji-Zhong, Zhang Zhi-Hai, Liu Sheng-Guang, Wang De-Zhen. Molecular dynamics simulation of energetic hydrogen isotopes bombarding the crystalline graphite(001). Acta Physica Sinica, 2012, 61(5): 055201. doi: 10.7498/aps.61.055201
[10]	Xia Wen-Ze, Yu Yong-Jiang, Yang Chuang-Lu. Influences of isotopic variant and collision energy on the stereodynamics of the N(4S)+H2 reactive system. Acta Physica Sinica, 2012, 61(22): 223401. doi: 10.7498/aps.61.223401
[11]	Liu Hui, Xing Wei, Shi De-Heng, Zhu Zun-Lue, Sun Jin-Feng. Study on spectroscopic parameters and molecular constants of CS+(X2Σ+) and CS+(A2Π) by MRCI. Acta Physica Sinica, 2011, 60(4): 043102. doi: 10.7498/aps.60.043102
[12]	Linghu Rong-Feng, Xu Mei, Wang Xiao-Lu, Lü Bing, Yang Xiang-Dong. The effect of symmetrical isotopic substitution in Ne-H2 collision. Acta Physica Sinica, 2010, 59(4): 2416-2422. doi: 10.7498/aps.59.2416
[13]	Xu Yan, Zhao Juan, Wang Jun, Liu Fang, Meng Qing-Tian. Influence of the collision energy and isotopic variant on the stereodynamics of reaction H+BrF→HBr+F. Acta Physica Sinica, 2010, 59(6): 3885-3891. doi: 10.7498/aps.59.3885
[14]	Yu Chun-Ri, Wang Rong-Kai, Zhang Jie, Yang Xiang-Dong. Differential cross sections for collisions between He isotope atoms and HBr molecules. Acta Physica Sinica, 2009, 58(1): 229-233. doi: 10.7498/aps.58.229
[15]	Sheng Zong-Qiang, Guo Jian-You. Systematic investigation of shape-coexistence in Se,Kr,Sr and Zr isotopes with relativistic mean field theory. Acta Physica Sinica, 2008, 57(3): 1557-1563. doi: 10.7498/aps.57.1557
[16]	Luo Wen-Lang, Ruan Wen, Zhang Li, Xie An-Dong, Zhu Zheng-He. Analytical potential energy function for tritium water molecule T2O(X1A1). Acta Physica Sinica, 2008, 57(8): 4833-4839. doi: 10.7498/aps.57.4833
[17]	Wang Rong-Kai, Shen Guang-Xian, Song Xiao-Shu, Linghu Rong-Feng, Yang Xiang-Dong. Influence of He isotope on the differential cross section for He-NO collision system. Acta Physica Sinica, 2008, 57(7): 4138-4142. doi: 10.7498/aps.57.4138
[18]	Zhang Li, Zhu Zheng-He, Yang Ben-Fu, Long Xing-Gui, Luo Shun-Zhong. Electron-vibration approximation method for hydrogen isotope compounds TiH2,TiD2 and TiT2. Acta Physica Sinica, 2006, 55(10): 5418-5423. doi: 10.7498/aps.55.5418
[19]	Zheng Li-Ping, Zhang Hu-Yong, Wang Ting-Tai, Ma Yu-Gang. Analysis of the contributions of PKA and SKA to the isotope enrichment. Acta Physica Sinica, 2004, 53(5): 1577-1582. doi: 10.7498/aps.53.1577
[20]	LI WEN-FEI, ZHANG FENG-SHOU, CHEN LIE-WEN. CHEMICAL INSTABILITY AND ISOSPIN EFFECTS IN ISOTOPIC DISTRIBUTIONS. Acta Physica Sinica, 2001, 50(6): 1040-1045. doi: 10.7498/aps.50.1040

2023年72卷182101-补充材料.ZIP

Catalog

Vol. 72, Issue 18 - 2023-09-20

Metrics

Abstract views: 2786
PDF Downloads: 44
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板