-
In this paper, we conduct the experiment and simulation on 31D5/2+6S1/2(F = 4) Cs2 ultralong-range Rydberg molecules (ULRMs). These molecules are prepared by employing a two-photon photoassociation scheme. Two distinct ultralong-range Rydberg molecular signals are observed at the detuning –162.8 MHz and –66.6 MHz of 31D5/2 atomic resonant line, which are bound by the pure triplet potential and mixed singlet-triplet potential, respectively. We use the model of scattering interaction between the Rydberg electron and ground-state atom to perform the simulation. The molecular potential-energy curves are obtained by solving the Hamiltonian on a grid of intermolecular distances R. The calculations of the binding energy of pure triplet and mixed singlet-triplet v = 0 vibrational states are compared with the experimental measurements. The calculated and measured values of the binding energy are in good agreement. The s-wave pure triplet and singlet zero-energy scattering length are obtained to be
${a}_{{\rm{s}}}^{{\rm{T}}}({0})=-{19.16}{a}_{0}$ and$ {a}_{{\rm{s}}}^{{\rm{S}}}(0)=-{1.92}{a}_{0} $ , respectively. This kind of molecule with large size, abundant vibrational states and large permanent electric dipole moment is an excellent candidate for studying low-energy collision dynamics. The study of these molecules will further deepen and enrich the understanding of the special binding mechanism and exotic properties of the ULRMs.-
Keywords:
- ultralong-range Rydberg molecules /
- low energy electron scattering /
- adiabatic potential energy curves /
- molecular vibration states
[1] Amaldi E, Segrè E 1934 Il Nuovo Cimento 11 145
Google Scholar
[2] Fermi E 1934 Il Nuovo Cimento 11 157
Google Scholar
[3] Valiron P, Roche A L, Masnou-Seeuws F, Dolan M E 1984 J. Phys. B: At. Mol. Phys. 17 2803
Google Scholar
[4] de Prunelé E 1987 Phys. Rev. A 35 496
Google Scholar
[5] Greene C H, Dickinson A S, Sadeghpour H R 2000 Phys. Rev. Lett. 85 2458
Google Scholar
[6] Bendkowsky V, Butscher B, Nipper J, Shaffer J P, Löw R, Pfau T 2009 Nature 458 1005
Google Scholar
[7] Bellos M A, Carollo R, Banerjee J, Eyler E E, Gould P L, Stwalley W C 2013 Phys. Rev. Lett. 111 053001
Google Scholar
[8] Anderson D A, Miller S A, Raithel G 2014 Phys. Rev. Lett. 112 163201
Google Scholar
[9] Krupp A T, Gaj A, Balewski J B, Ilzhöfer P, Hofferberth S, Löw R, Pfau T, Kurz M, Schmelcher P 2014 Phys. Rev. Lett. 112 143008
Google Scholar
[10] Tallant J, Rittenhouse S T, Booth D, Sadeghpour H R, Shaffer J P 2012 Phys. Rev. Lett. 109 173202
Google Scholar
[11] Booth D, Rittenhouse S T, Yang J, Sadeghpour H R, Shaffer J P 2015 Science 348 99
Google Scholar
[12] Bendkowsky V, Butscher B, Nipper J, Balewski J B, Shaffer J P, Löw R, Pfau T 2010 Phys. Rev. Lett. 105 163201
Google Scholar
[13] Fabrikant I I 1986 J. Phys. B: At. Mol. Phys. 19 1527
Google Scholar
[14] Bahrim C, Thumm U, Fabrikant I I 2001 J. Phys. B: At. Mol. Opt. Phys. 34 L195
Google Scholar
[15] Anderson D A, Miller S A, Raithel G 2014 Phys. Rev. A 90 062518
Google Scholar
[16] Saßmannshausen H, Merkt F, Deiglmayr J 2015 Phys. Rev. Lett. 114 133201
Google Scholar
[17] Maclennan J L, Chen Y J, Raithel G 2019 Phys. Rev. A 99 033407
Google Scholar
[18] Bai S, Han X, Bai J, Jiao Y, Zhao J, Jia S, Raithel G 2020 Phys. Rev. Res. 2 033525
Google Scholar
[19] Omont A 1977 J. Phys. 38 1343
Google Scholar
[20] Bai S Y, Bai J X, Han X X, Jiao Y C, Zhao J M, Jia S T 2020 Chin. Phys. Lett. 37 123201
Google Scholar
[21] 焦月春, 白景旭, 宋蓉, 韩小萱, 赵建明 2023 72 033202
Google Scholar
Jiao Y C, Bai J X, Song R, Han X X, Zhao J M 2023 Acta Phys. Sin. 72 033202
Google Scholar
[22] Yang Y, Kühn O 2008 Mol. Phys. 106 2445
Google Scholar
[23] Yang Y, Meuwly M 2010 J. Chem. Phys. 133 064503
Google Scholar
[24] Yang Y, Liu X, Meuwly M, Xiao L, Jia S 2012 J. Phys. Chem. A 116 11134
Google Scholar
[25] Hamilton E L, Greene C H, Sadeghpour H R 2002 J. Phys. B: At. Mol. Opt. Phys. 35 L199
Google Scholar
[26] Khuskivadze A A, Chibisov M I, Fabrikant I I 2002 Phys. Rev. A 66 042709
Google Scholar
[27] Bahrim C, Thumm U 2000 Phys. Rev. A 61 022722
Google Scholar
[28] Markson S, Rittenhouse S T, Schmidt R, Shaffer J P, Sadeghpour H R 2016 Chemphyschem 17 3683
Google Scholar
-
图 1 (a)双光子光缔合激发示意图, 第1个852 nm的光子完成
$|\text{6}{\text{S}}_{\text{1/2}},{F}\text{=4}\rangle\to |\text{6}{\text{P}}_{\text{3/2}},{{F}}'\text{=5}\rangle$ 的原子跃迁, 第2个510 nm光子将$|\text{6}{\text{P}}_{\text{3/2}}, {{F}}'\text{=5}\rangle$ 态的原子激发到$ |\text{31}{\text{D}}_{\text{5/2}}\rangle $ 态, 使用双通声光调制器(AOM)将852 nm激光频率从$|\text{6}{\text{P}}_{\text{3/2}}, {{F}}'\text{=5}\rangle$ 能级向蓝失谐方向频移360 MHz, 510 nm激光频率从31D5/2里德伯原子能级共振线向红失谐方向扫描, 当激光能量与分子能级匹配时就形成了长程里德伯分子; (b)时序图, MOT光和ODT光关断后, 打开852 nm和510 nm激发光来制备里德伯原子和长程里德伯分子, 随后施加斜坡电离电场使得里德伯原子和分子自电离产生的离子加速到达MCP进行收集探测; (c)实验制备长程里德伯分子示意图, 852 nm(红色光束)和510 nm(绿色光束)激发光反向传播通过装载于偶极阱(黄色光束)中的铯冷原子团中心, 并将基态原子激发形成里德伯原子和分子Figure 1. (a) Two-photon potoassociation excitation diagram, the first photon, 852 nm laser, drives the
$|\text{6}{\text{S}}_{\text{1/2}}, \text{}{F}=4 \rangle\to $ $ |\text{6}{\text{P}}_{\text{3/2}}, \text{}{{F}}' =5\rangle$ transition, and the second photon, 510 nm laser, drives the$ |\text{6}{\text{P}}_{\text{3/2}}\text{, }{\text{}{F}}'\text{=5}\rangle\to |\text{31}{\text{D}}_{\text{5/2}}\rangle $ transition, the 852 nm laser frequency is blue shifted from$|\text{6}{\text{P}}_{\text{3/2}}, {{F}}'\text{=5}\rangle$ by 360 MHz using a double-pass acousto-optic modulator (AOM), the 510 nm laser frequency is scanned to red detuning from the 31D5/2 Rydberg atomic line, Rydberg molecules are formed when the detuning from the atomic line matches a molecular binding energy; (b) timing sequence, after switching off the MOT and ODT beams, the 852 nm and 510 nm lasers are used to excite ground state cesium atoms to form the Rydberg atoms and molecules, a ramped electric field is finally applied to accelerate the ions that are produced by autoionization to MCP for collection and detection; (c) experimental schematic of ultralong-range Rydberg molecules, the 852 nm (red beam) and 510 nm (green beam) lasers counterpropagate through a cold Cs atom cloud located in a crossed optical dipole trap (yellow beams) and excite ground state atoms to form Rydberg atoms and molecules.
图 2 实验测量的31D5/2+6S1/2(F = 4)长程里德伯分子光缔合光谱. 0 MHz处是31D5/2里德伯原子共振线, 失谐–162.8 MHz和–66.6 MHz处的两个小峰分别来自纯三重态势阱和混合单重态-三重态势阱形成的长程里德伯分子信号. 黑色圆点是实验测量值, 由6组独立实验数据平均后得到, 误差是6组独立测量的标准误差, 红色实线是对数据平滑后的结果
Figure 2. The photoassosiation spectra of 31D5/2+6S1/2(F = 4) long-range Rydberg molecules. The position of 0-detuning resonant excitation is 31D5/2 atoms signal. The two small peaks at detuning, –162.8 MHz and –66.6 MHz, are the long-range Rydberg molecules signals, and they are induced due to the pure triplet potential and mixed singlet and triplet potential. The black symbols show the experimental measurement of six groups of indepenent data, and the error bars are the standard errors of six independent measurements. The red solid line displays smoothed average.
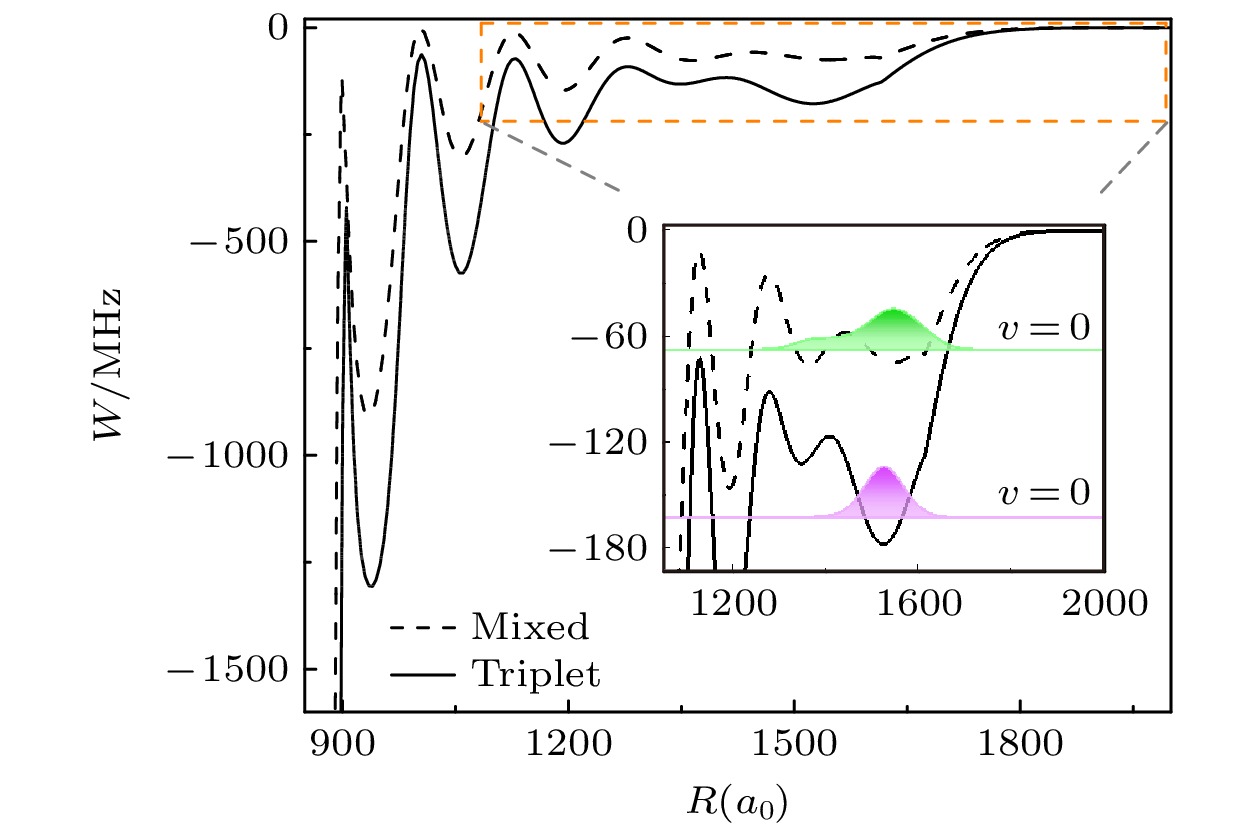
图 3 理论计算的31D5/2+6S1/2(F = 4)长程里德伯分子绝热势能曲线, 黑色虚线是由单重态-三重态超精细混合产生的浅势阱, 黑色实线是纯三重态散射形成的深势阱. 插图是橙色虚线方框部分放大后的结果, 绿色和粉色填充线分别是浅势阱和深势阱v = 0的分子振动波函数
Figure 3. The calculations of potential energy curves of 31D5/2+6S1/2(F = 4) long-range Rydberg molecules. The shallow potential (dashed black) comes from hyperfine-mixed singlet-triplet scattering, and the deep potential (solid black) is due to the pure triplet scattering. The inset is an enlargement of orange region. The vibrational wave functions in the outermost wells are indicated in color filled curves for v = 0 of shallow (green) and deep (pink) potential.
图 4 铯电子-原子(6S)低能散射相移, 1s和3s是调整后的s-波单重态和三重态散射相移, p-波散射相移仍使用Khuskivadze等[26]提供的非相对论函数
Figure 4. Phase shifts for low-energy electron scattering from Cs. The 1s and 3s are adjusted s-wave singlet and triplet scattering phase shift, respectively. For p-wave phase shifts we still used nonrelativistic functions provided by Khuskivadze et al.[26].
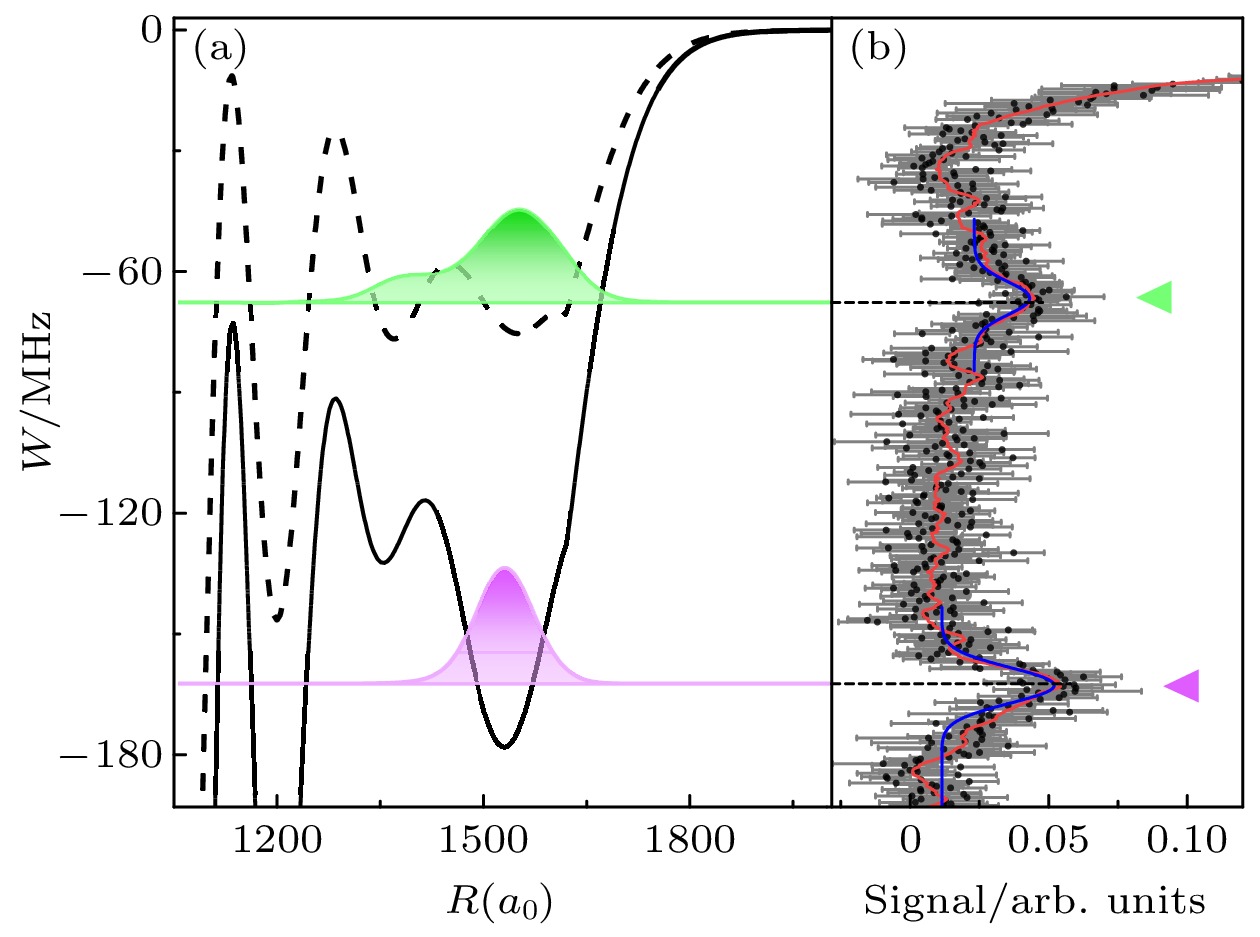
图 5 31D5/2+6S1/2(F = 4)长程里德伯分子理论计算与实验测量的比较 (a)理论计算的31D5/2+6S1/2(F = 4)长程里德伯分子绝热势能曲线和最外层势阱的分子振动基态波函数, 绿色和粉色填充线分别是单重态-三重态超精细混合浅势阱(虚线)和纯三重态散射深势阱(实线)v = 0的振动波函数; (b)实验测量的31D5/2+6S1/2(F = 4)长程里德伯分子光谱, 绿色和粉色三角标注的两个小峰分别来自混合单重态-三重态势阱和纯三重态势阱形成的长程里德伯分子信号, 图中的蓝色曲线是对分子信号进行高斯拟合后的结果
Figure 5. Comparison between calculated potential energy curves and experimental measurement of 31D5/2+6S1/2(F = 4) long-range Rydberg molecules: (a) The calculations of 31D5/2+6S1/2(F = 4) long-range Rydberg molecules potential energy curves and the vibrational wave functions in the outermost wells, the green and pink color filled curves are v = 0 vibrational wave functions of hyperfine-mixed singlet-triplet potential and pure triplet potential, respectively; (b) the measurments of 31D5/2+6S1/2(F = 4) long-range Rydberg molecules, the two peaks marked with green and pink triangles are mixed and triplet molecules signals, respectively, the blue solid lines are Gaussian fittings to the molecular peaks.
表 1 理论计算与实验测量的混合态和三重态分子v = 0振动基态束缚能的比较, 计算中使用s-波零能散射长度
$ {a}_{{\rm{s}}}^{{\rm{S}}}\left(0\right)=-1.92{a}_{0} $ 和$ {a}_{{\rm{s}}}^{{\rm{T}}}\left(0\right)=-\text{19.}\text{16}{a}_{0} $ Table 1. Comparison of theoretical calculation and experimental measurement of the ground state binding energy of mixed state and triplet state molecule with v = 0 vibration, the s-wave zero energy scattering length of
${a}_{{\rm{s}}}^{{\rm{S}}}(0) = -1.92{a}_{0}$ and${a}_{{\rm{s}}}^{{\rm{T}}}(0) = -19.16{a}_{0}$ is used in the calculation.Mixed/MHz Triplet/MHz Theo. –67.7 –162.4 Exp. –66.6 ± 0.6 –162.8 ± 0.4 
DownLoad: CSV
-
[1] Amaldi E, Segrè E 1934 Il Nuovo Cimento 11 145
Google Scholar
[2] Fermi E 1934 Il Nuovo Cimento 11 157
Google Scholar
[3] Valiron P, Roche A L, Masnou-Seeuws F, Dolan M E 1984 J. Phys. B: At. Mol. Phys. 17 2803
Google Scholar
[4] de Prunelé E 1987 Phys. Rev. A 35 496
Google Scholar
[5] Greene C H, Dickinson A S, Sadeghpour H R 2000 Phys. Rev. Lett. 85 2458
Google Scholar
[6] Bendkowsky V, Butscher B, Nipper J, Shaffer J P, Löw R, Pfau T 2009 Nature 458 1005
Google Scholar
[7] Bellos M A, Carollo R, Banerjee J, Eyler E E, Gould P L, Stwalley W C 2013 Phys. Rev. Lett. 111 053001
Google Scholar
[8] Anderson D A, Miller S A, Raithel G 2014 Phys. Rev. Lett. 112 163201
Google Scholar
[9] Krupp A T, Gaj A, Balewski J B, Ilzhöfer P, Hofferberth S, Löw R, Pfau T, Kurz M, Schmelcher P 2014 Phys. Rev. Lett. 112 143008
Google Scholar
[10] Tallant J, Rittenhouse S T, Booth D, Sadeghpour H R, Shaffer J P 2012 Phys. Rev. Lett. 109 173202
Google Scholar
[11] Booth D, Rittenhouse S T, Yang J, Sadeghpour H R, Shaffer J P 2015 Science 348 99
Google Scholar
[12] Bendkowsky V, Butscher B, Nipper J, Balewski J B, Shaffer J P, Löw R, Pfau T 2010 Phys. Rev. Lett. 105 163201
Google Scholar
[13] Fabrikant I I 1986 J. Phys. B: At. Mol. Phys. 19 1527
Google Scholar
[14] Bahrim C, Thumm U, Fabrikant I I 2001 J. Phys. B: At. Mol. Opt. Phys. 34 L195
Google Scholar
[15] Anderson D A, Miller S A, Raithel G 2014 Phys. Rev. A 90 062518
Google Scholar
[16] Saßmannshausen H, Merkt F, Deiglmayr J 2015 Phys. Rev. Lett. 114 133201
Google Scholar
[17] Maclennan J L, Chen Y J, Raithel G 2019 Phys. Rev. A 99 033407
Google Scholar
[18] Bai S, Han X, Bai J, Jiao Y, Zhao J, Jia S, Raithel G 2020 Phys. Rev. Res. 2 033525
Google Scholar
[19] Omont A 1977 J. Phys. 38 1343
Google Scholar
[20] Bai S Y, Bai J X, Han X X, Jiao Y C, Zhao J M, Jia S T 2020 Chin. Phys. Lett. 37 123201
Google Scholar
[21] 焦月春, 白景旭, 宋蓉, 韩小萱, 赵建明 2023 72 033202
Google Scholar
Jiao Y C, Bai J X, Song R, Han X X, Zhao J M 2023 Acta Phys. Sin. 72 033202
Google Scholar
[22] Yang Y, Kühn O 2008 Mol. Phys. 106 2445
Google Scholar
[23] Yang Y, Meuwly M 2010 J. Chem. Phys. 133 064503
Google Scholar
[24] Yang Y, Liu X, Meuwly M, Xiao L, Jia S 2012 J. Phys. Chem. A 116 11134
Google Scholar
[25] Hamilton E L, Greene C H, Sadeghpour H R 2002 J. Phys. B: At. Mol. Opt. Phys. 35 L199
Google Scholar
[26] Khuskivadze A A, Chibisov M I, Fabrikant I I 2002 Phys. Rev. A 66 042709
Google Scholar
[27] Bahrim C, Thumm U 2000 Phys. Rev. A 61 022722
Google Scholar
[28] Markson S, Rittenhouse S T, Schmidt R, Shaffer J P, Sadeghpour H R 2016 Chemphyschem 17 3683
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2913
- PDF Downloads: 76
- Cited By: 0
