-
In the process of production or long-time use of a thin metal plate, micro defects (micro particles or pores) will be produced in its interior. The number and size of these micro defects determine the quality of the thin metal plate, affecting its service life and factor of safety. Therefore, quantitative and accurate characterization of micro defects is a necessary to ensure the quality and safety of thin metal plate products. In this work, we study the application of motion induced eddy current magnetic field testing in electromagnetic testing to detect defects in conductive material and nonmagnetic material. The simulation results show that when the lift-ff distance and the surface remanence of the permanent magnet are determined, the size of the permanent magnet is positively correlated with the amplitude of the defect detection signal. The main reason is that in a motion induced electric field without defects, the amplitude of defect detection signal is linearly related to the current density mode at each point on the defect motion path. Increasing the size of the permanent magnet can effectively improve the current density mode. As a continuation of the above results, an optimization method for excitation magnetic field in motion induced eddy current magnetic field detection is proposed. The two types of permanent magnet arrays generated by this method generate larger amplitude defect detection signals than that by simple permanent magnets with the same volume and surface residual magnetism. The experimental results show that the excitation magnetic field arrangement designed by the above optimization method increases the signal amplitude by 80%–90% compared with that by traditional method. This optimization method conduces to improving the sensitivity of motion induced eddy current magnetic field detection methods.
-
Keywords:
- motion induced eddy current /
- conductive nonmagnetic materials /
- electromagnetic nondestructive testing
[1] Gras C H, Meredith M, Gatenby K, Hunt J D 2002 Mater. Sci. Forum 396 89
Google Scholar
[2] 栾小东, 宋宝韫, 李冰 2010 热加工工艺 39 164
Google Scholar
Luan X D, Song B Y, Li B 2010 Hot Working Technol. 39 164
Google Scholar
[3] Mukherjee M, Garcia-Moreno F, Banhart J 2010 Scripta Mater. 63 235
Google Scholar
[4] Hao R Y, Lu B Y, Cheng Y, Li X, Huang B Q 2020 J. Intell. Manuf. 32 1833
Google Scholar
[5] Budhia M, Boys J T, Covic G A, Huang C Y 2013 IEEE T. Ind. Electron. 60 318
Google Scholar
[6] Chandra S A, Kim J, Le M, Lee J 2014 IEEE T. Magn. 50 11
Google Scholar
[7] Hajime T, Yasuo T, Makoto A, Takuya Y, Toshihiro S 2011 Mater. Trans. 52 531
Google Scholar
[8] Zhu Y, Wang K C, Kang L, Zhai G F, Wang S J 2010 Proceedings of the 5th IEEE Conference on Industrial Taichung, Taiwan, China, June 15–17, 2010 p228
[9] Ozgul K, Murat D 2007 J. Mater. Process. Techn. 186 125
Google Scholar
[10] Li Y, Trinh H, Haas N, Otto C, Pankanti S 2014 IEEE T. Intell. Transp. 15 760
Google Scholar
[11] Pasadas D, Rocha T J, Ramos H G, Ribeiro A L 2012 Measurement 45 393
Google Scholar
[12] Pohl R, Erhard A, Montag H J, Thomas H M, Wustenberg H 2003 NDT & E Int. 37 89
Google Scholar
[13] Bernieri A, Betta G, Ferrigno L, Laracca M, Mastrostefano S 2014 IEEE T. Instrum. Meas. 63 1272
Google Scholar
[14] Pasadas D J, Rocha T J, Ramos H G, Ribeiro A L 2013 IEEE International Instrumentation and Measurement Technology Minneapolis, MN May 6–9, 2013 p391
[15] Rocha T J, Ramos H G, Ribeiro A L, Pasadas D J 2016 IEEE T. Instrum. Meas. 65 1182
Google Scholar
[16] Feng B, Kang Y H, Sun Y H, Yang Y, Yan X Z 2016 Int. J. Appl. Electrom. 52 357
Google Scholar
[17] Brauer H, Otterbach J M, Ziolkowski M, Toepfer H, Graetzel M, Bergmann J P 2018 45th Annual Review of Progress in Quantitative Nondestructive Evaluation Conference Burlington, VT July 15–19, 2018 p2102
[18] Yuan F, Yu Y T, Li L F, Tian G Y 2021 IEEE Sens. J. 21 7449
Google Scholar
[19] Rocha T J, Ramos H G, Ribeiro A L, Pasadas D J, Angan C S 2015 Measurement 67 108
Google Scholar
[20] Wang X D, Thess A, Moreau R, Tan Y Q, Dai S J, Tao Z, Yang W Z, Wang B 2016 J. Appl. Phys. 120 014903
Google Scholar
[21] Brauer H, Porzig K, Mengelkamp J, Carlstedt M, Ziolkowski M, Toepfer H 2013 17th International Symposium on Theoretical Electrical Engineering Pilsen, Czech Republic, 2013 33 1965
[22] Matthias C, Konstantin P, Robert P U, Mladen Z, Marek Z, Hartmut B 2014 Int. J. Appl. Electrom. 45 519
Google Scholar
[23] Marek Z, Jan-Marc O, Reinhard S, Hartmut B, Hannes T 2020 IEEE T. Magn. 56 19404471
Google Scholar
[24] Moreau R, Tao Z, Wang X D 2016 Appl. Phys. Lett. 109 024104
Google Scholar
[25] Feng B, Ribeiro A L, Rocha T J, Ramos H G 2018 Sensors 18 3199
Google Scholar
-
图 1 运动感应涡流检测原理 (a)无缺陷; (b)有缺陷
Figure 1. Principle of motion induced eddy current testing: (a) Without defect; (b) with defect.
图 2 数学模型示意图
Figure 2. Schematic diagram of mathematical model.
图 3 永磁体尺寸对缺陷运动路径上各点处电流密度的Y方向分量的影响
Figure 3. Influence of permanent magnet size on the Y-direction component of current density at each point on the defect motion path.
图 4 永磁体尺寸与原点处电流密度模的关系
Figure 4. Relationship between permanent magnet size and current density mode at the origin.
图 5 永磁体尺寸与原点处第一磁场Z方向分量的关系
Figure 5. Relationship between permanent magnet size and Z direction component of the first magnetic field at the origin.
图 6 缺陷移动位置X与点探针处磁通密度的X方向变化量曲线
Figure 6. Curve of defect moving position X and X direction change of magnetic flux density at point probe.
图 7 原点处电流密度模与信号幅值关系
Figure 7. Relation between current density mode at origin and signal amplitude.
图 8 微分单元选取示意图
Figure 8. Schematic diagram of differential unit selection.
图 9 永磁体依据运动感应涡流在原点处的电势与电流密度贡献分区, 图中假设永磁体磁化方向为
$e_{\textit{Z}}$ 方向, 即永磁体N级为Z+方向, 导体板运动方向为X+方向Figure 9. Permanent magnet is divided according to the potential and current density contribution of the motion induced eddy current at the origin. In the figure, it is assumed that the magnetization direction of the permanent magnet is
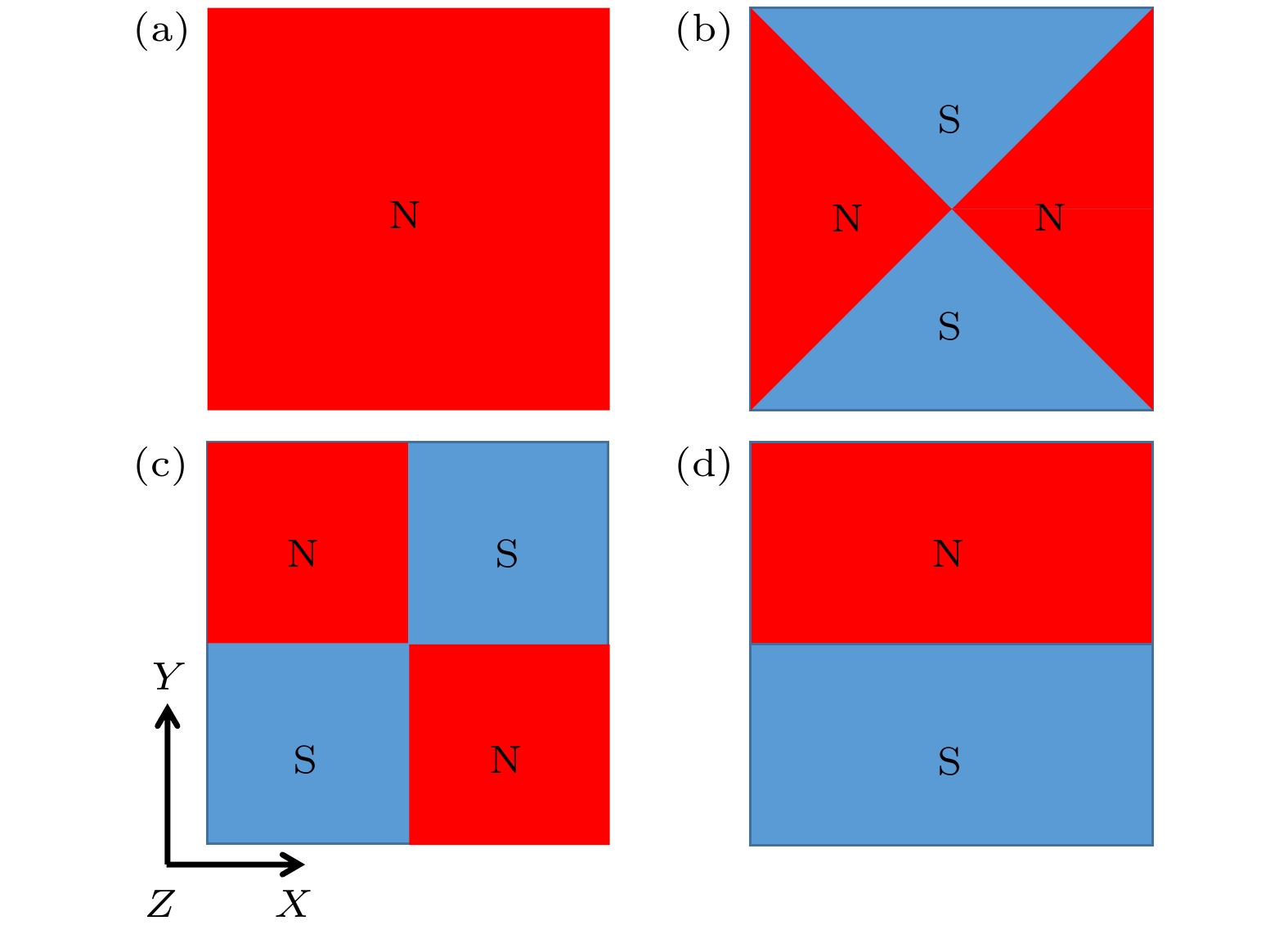
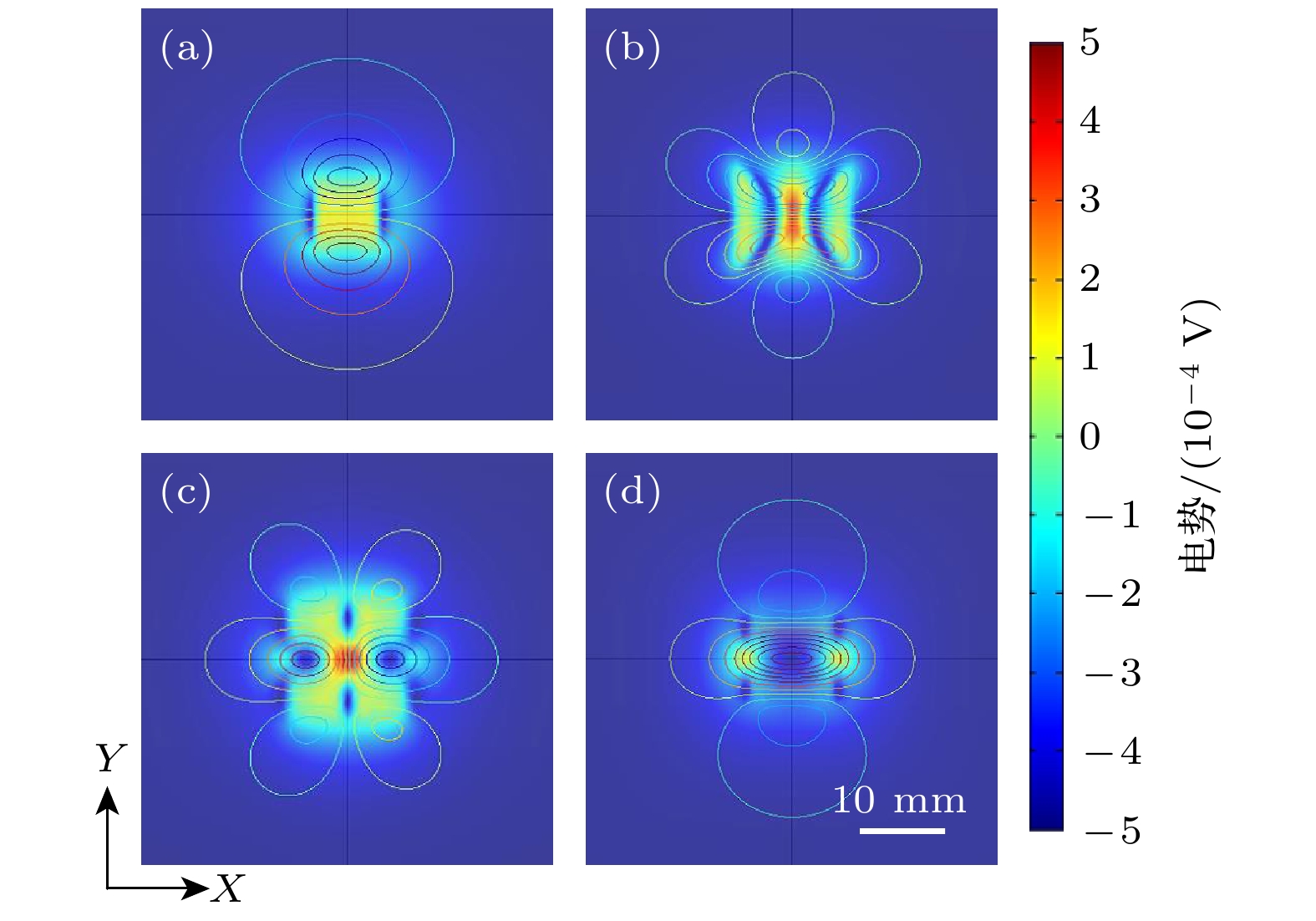
$e_{\textit{Z}}$ direction, that is, the permanent magnet N is Z+ direction, and the movement direction of the conductor plate is X+ direction.
图 10 第一磁场设置 (a)原始设置; (b)聚Y方向电流设置; (c)聚X方向电流设置; (d)聚集电势设置(表面剩磁方向平行于Z轴; 导电板相对速度方向平行于X轴)
Figure 10. Setting of the first magnetic field: (a) Original pattern; (b) pattern focusing current in Y direction; (c) pattern focusing current in X direction; (d) pattern focusing potential (The direction of surface remanence is parallel to the Z-axis; the relative velocity direction is parallel to the X-axis).
图 11 原始及3种优化设置涡电流场电流密度分布
Figure 11. Eddy current field current density distribution of original and three optimized patterns.
图 12 原始及3种优化设置涡电流场等势线分布
Figure 12. Equipotential distribution of eddy current field in the original and three optimized patterns.
图 13 各永磁体设置下的缺陷信号
Figure 13. Defect signal at each permanent magnet patterns.
图 14 实验结构
Figure 14. Experimental structure.
图 15 三种永磁体设置
Figure 15. Three permanent magnet settings.
图 16 改变永磁体尺寸对缺陷信号的影响 (a) D = 3 mm; (b) D = 4 mm; (c) D = 5 mm
Figure 16. Effect of changing permanent magnet size on defect signal: (a) D = 3 mm; (b) D = 4 mm; (c) D = 5 mm.
图 17 聚Y方向电流设置与聚X方向电流设置下的缺陷信号 (a) D = 3 mm; (b) D = 4 mm; (c) D = 5 mm
Figure 17. Defect signal under current patterns of poly Y direction and poly X direction: (a) D = 3 mm; (b) D = 4 mm; (c) D = 5 mm.
表 1 常见物质相对磁导率
Table 1. Relative permeability of common materials
物质 温度/°C μr 真空 — 1 空气 (标准状态) 1.00000004 Al 20 1.000022 Cu 20 0.99990 O2 (标准状态) 1.0000019 Pt 20 1.00026 Ag 20 0.999974 岩盐 20 0.9996 
DownLoad: CSV
表 2 数值模拟部分参数
Table 2. Parameters of numerical simulation.
导电板尺寸/mm3 200 × 200 × 0.5 电导率/(S·m–1) 5.998 × 107 相对磁导率 1.0 相对速度/(m·s–1) 0.5
微缺陷尺寸/mm3 0.5 × 0.5 × 0.5 电导率/(S·m–1) 0 相对磁导率 1.0
永磁体表面剩余磁通密度/T Norm Br 回复磁导率 1.05 提离距离/mm 1.0
空气电导率/(S·m–1) 0 相对磁导率 1.0 域尺寸/mm3 250 × 250 × 70
DownLoad: CSV
表 3 数值模拟结果
Table 3. List of numerical simulation results.
永磁体设置 原点处电流密度/(A·m–2) 原点处电势/V 其他 原始设置 $ J_y^O $= –11421832 VO = 7.7248×10–7 — 聚Y方向电流设置 $ J_y^{FY} $ = 15720916 VFY = 5.028×10–7 |$ J_y^{FY} $|=1.38×|$ J_y^O $| 聚X方向电流设置 $ J_x^{FX} $= 17627215 VFX = 5.499×10–6 |$ J_x^{FX} $|=1.54×|$ J_y^O $|
聚集电势设置
$ J_y^{FP} $= –70201
VFP = 1.0601×10–3当 x = ±5 mm, 电流密度模取最大值: Jx (x = 5) = 1.08×107 A/m2, |Jx (x = 5)| = 0.95×|$ J_y^O $|
DownLoad: CSV
表 4 模拟部分参数
Table 4. Parameter of simulation part.
导电板 相对速度/(m·s–1) 0.2 厚度/mm 0.5 微缺陷 尺寸/mm3 2.0 × 2.0 × 0.5 永磁体 尺寸/mm3 20 × 20 × 20 提离距离/mm 1.0 磁通密度探针 探针高度/mm 0.5
DownLoad: CSV
表 5 实验参数
Table 5. List of experimental parameters.
导电板材料 Cu 缺陷处速度/(m·s–1) 0.2 厚度/mm 0.5 微缺陷 直径/mm 3, 4, 5
永磁体表面剩余磁通密度/Gs 440 提离距离/mm 3.5
传感器传感器类型 通用多功能
线性TMR传感器灵敏度/(mV·V–1·Oe–1) 3.1 激励电压/V 6.0
DownLoad: CSV
-
[1] Gras C H, Meredith M, Gatenby K, Hunt J D 2002 Mater. Sci. Forum 396 89
Google Scholar
[2] 栾小东, 宋宝韫, 李冰 2010 热加工工艺 39 164
Google Scholar
Luan X D, Song B Y, Li B 2010 Hot Working Technol. 39 164
Google Scholar
[3] Mukherjee M, Garcia-Moreno F, Banhart J 2010 Scripta Mater. 63 235
Google Scholar
[4] Hao R Y, Lu B Y, Cheng Y, Li X, Huang B Q 2020 J. Intell. Manuf. 32 1833
Google Scholar
[5] Budhia M, Boys J T, Covic G A, Huang C Y 2013 IEEE T. Ind. Electron. 60 318
Google Scholar
[6] Chandra S A, Kim J, Le M, Lee J 2014 IEEE T. Magn. 50 11
Google Scholar
[7] Hajime T, Yasuo T, Makoto A, Takuya Y, Toshihiro S 2011 Mater. Trans. 52 531
Google Scholar
[8] Zhu Y, Wang K C, Kang L, Zhai G F, Wang S J 2010 Proceedings of the 5th IEEE Conference on Industrial Taichung, Taiwan, China, June 15–17, 2010 p228
[9] Ozgul K, Murat D 2007 J. Mater. Process. Techn. 186 125
Google Scholar
[10] Li Y, Trinh H, Haas N, Otto C, Pankanti S 2014 IEEE T. Intell. Transp. 15 760
Google Scholar
[11] Pasadas D, Rocha T J, Ramos H G, Ribeiro A L 2012 Measurement 45 393
Google Scholar
[12] Pohl R, Erhard A, Montag H J, Thomas H M, Wustenberg H 2003 NDT & E Int. 37 89
Google Scholar
[13] Bernieri A, Betta G, Ferrigno L, Laracca M, Mastrostefano S 2014 IEEE T. Instrum. Meas. 63 1272
Google Scholar
[14] Pasadas D J, Rocha T J, Ramos H G, Ribeiro A L 2013 IEEE International Instrumentation and Measurement Technology Minneapolis, MN May 6–9, 2013 p391
[15] Rocha T J, Ramos H G, Ribeiro A L, Pasadas D J 2016 IEEE T. Instrum. Meas. 65 1182
Google Scholar
[16] Feng B, Kang Y H, Sun Y H, Yang Y, Yan X Z 2016 Int. J. Appl. Electrom. 52 357
Google Scholar
[17] Brauer H, Otterbach J M, Ziolkowski M, Toepfer H, Graetzel M, Bergmann J P 2018 45th Annual Review of Progress in Quantitative Nondestructive Evaluation Conference Burlington, VT July 15–19, 2018 p2102
[18] Yuan F, Yu Y T, Li L F, Tian G Y 2021 IEEE Sens. J. 21 7449
Google Scholar
[19] Rocha T J, Ramos H G, Ribeiro A L, Pasadas D J, Angan C S 2015 Measurement 67 108
Google Scholar
[20] Wang X D, Thess A, Moreau R, Tan Y Q, Dai S J, Tao Z, Yang W Z, Wang B 2016 J. Appl. Phys. 120 014903
Google Scholar
[21] Brauer H, Porzig K, Mengelkamp J, Carlstedt M, Ziolkowski M, Toepfer H 2013 17th International Symposium on Theoretical Electrical Engineering Pilsen, Czech Republic, 2013 33 1965
[22] Matthias C, Konstantin P, Robert P U, Mladen Z, Marek Z, Hartmut B 2014 Int. J. Appl. Electrom. 45 519
Google Scholar
[23] Marek Z, Jan-Marc O, Reinhard S, Hartmut B, Hannes T 2020 IEEE T. Magn. 56 19404471
Google Scholar
[24] Moreau R, Tao Z, Wang X D 2016 Appl. Phys. Lett. 109 024104
Google Scholar
[25] Feng B, Ribeiro A L, Rocha T J, Ramos H G 2018 Sensors 18 3199
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2646
- PDF Downloads: 60
- Cited By: 0
