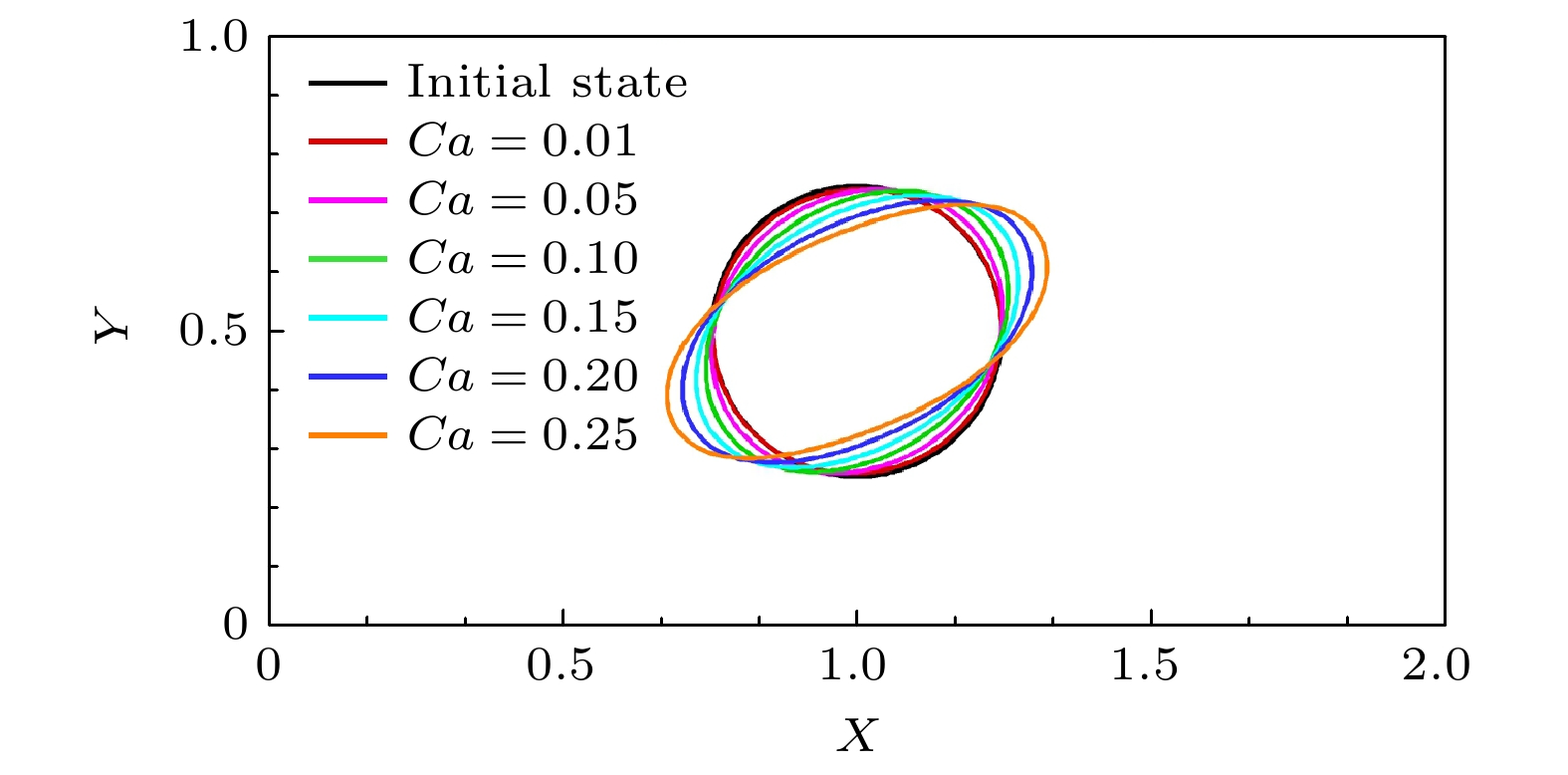
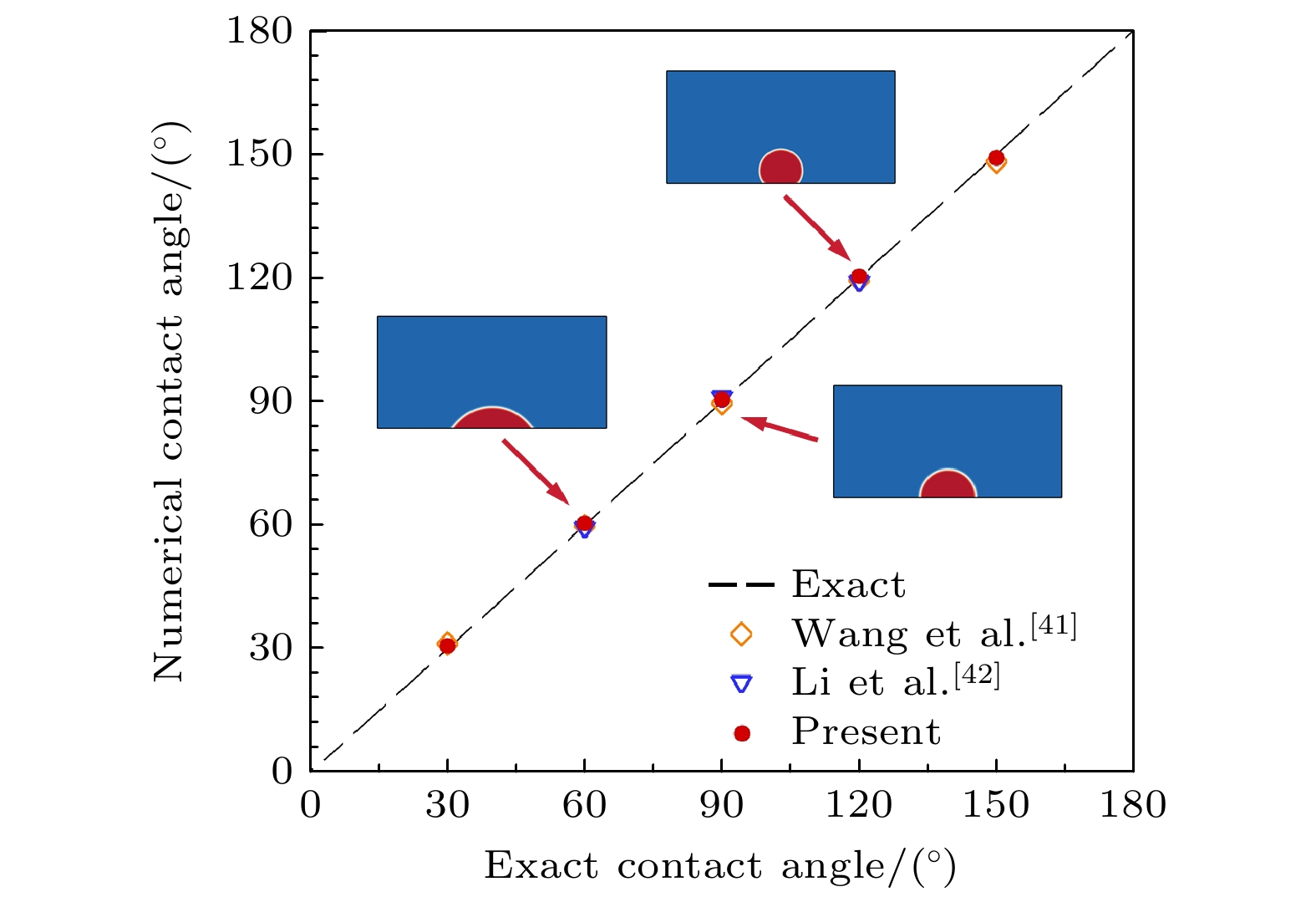
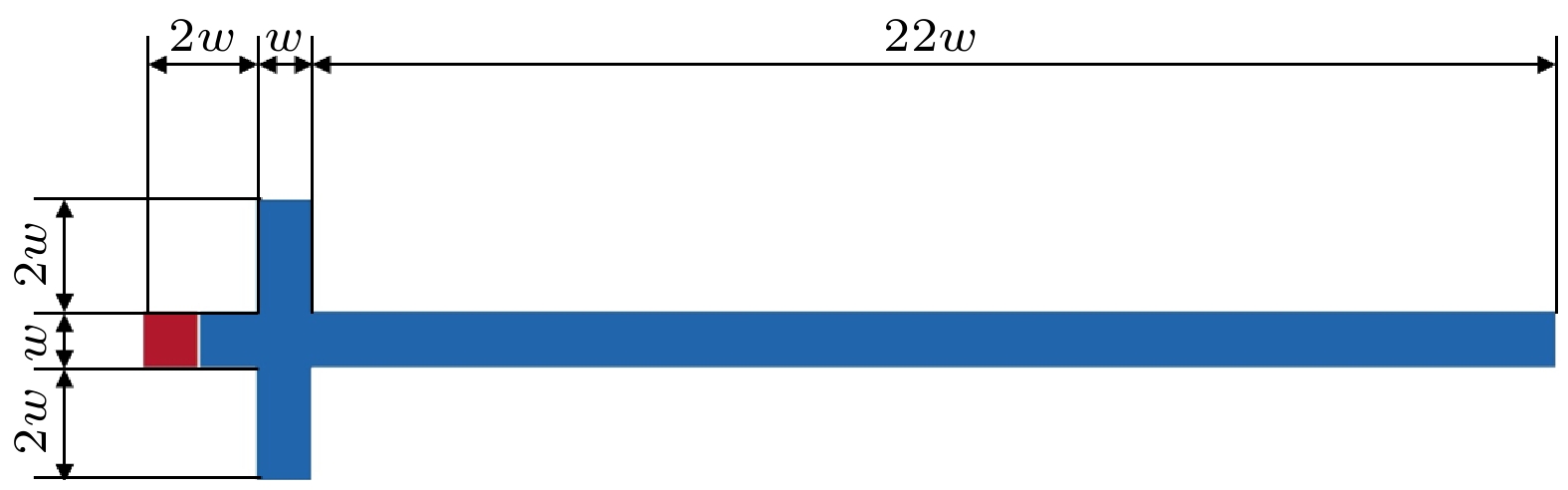
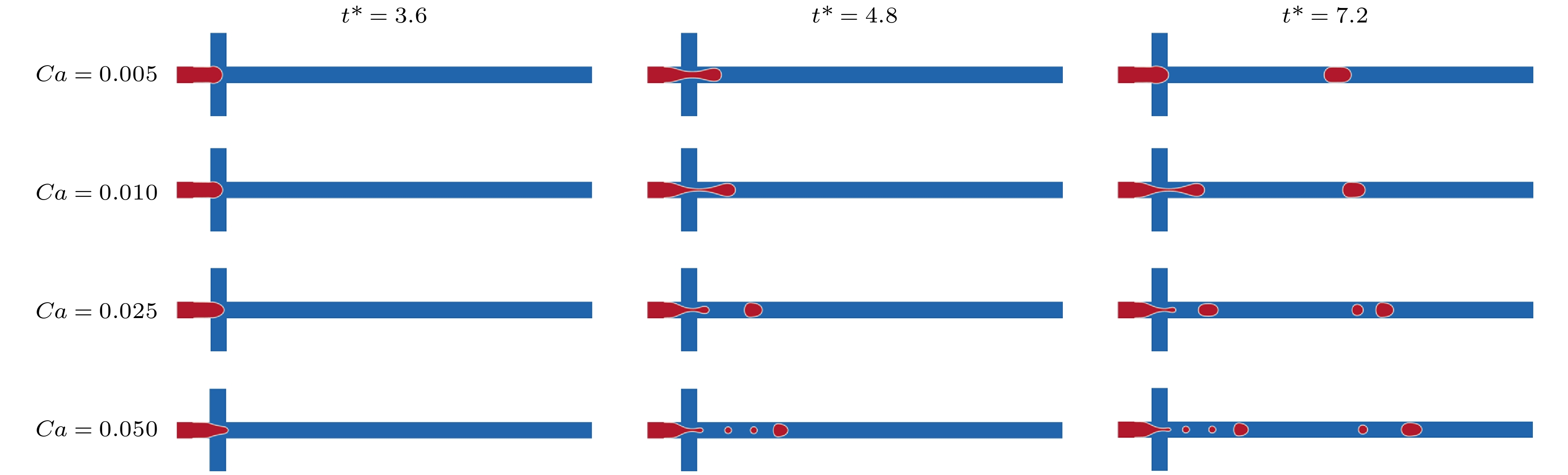
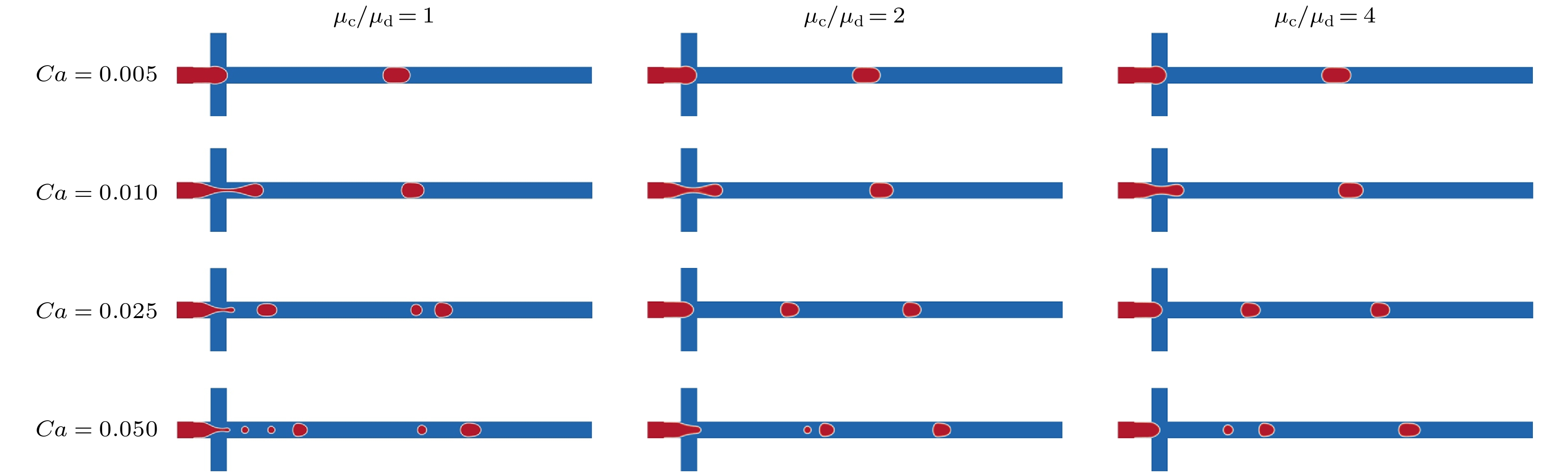
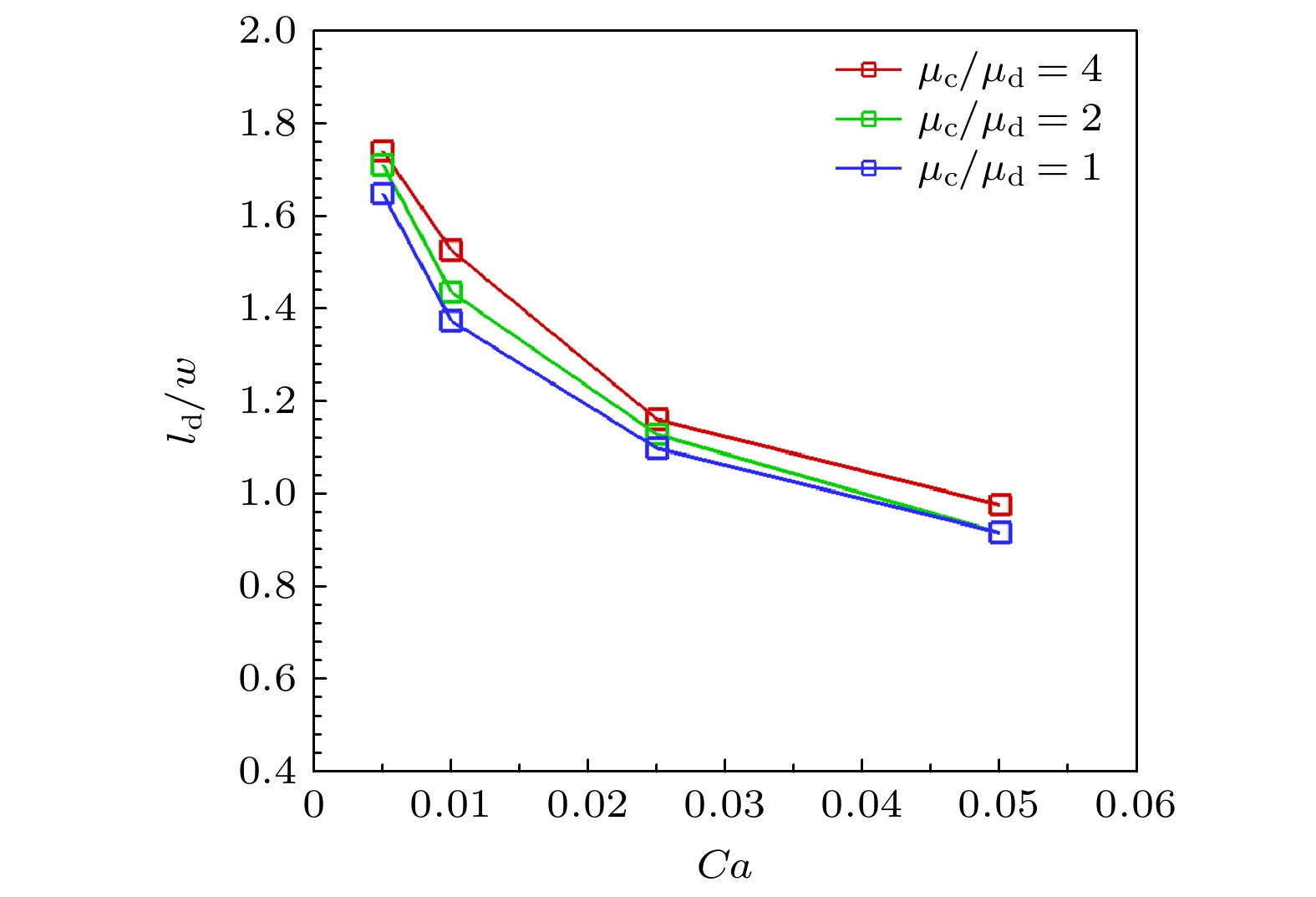
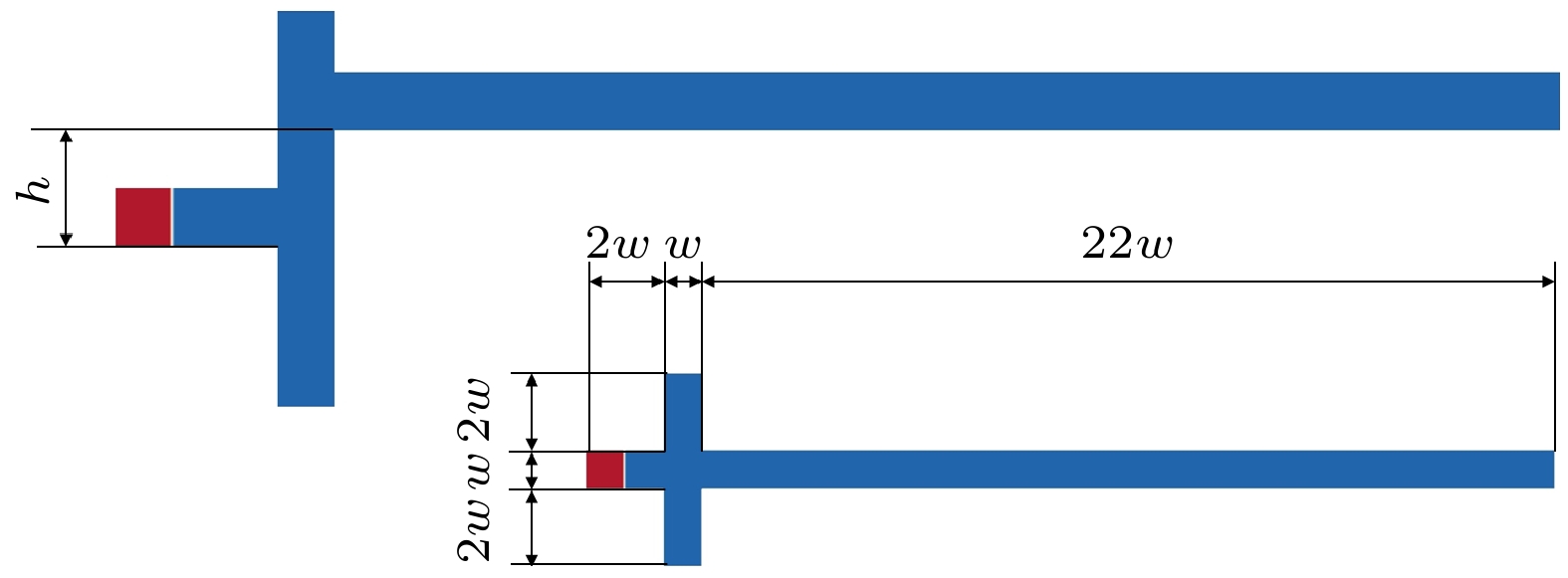
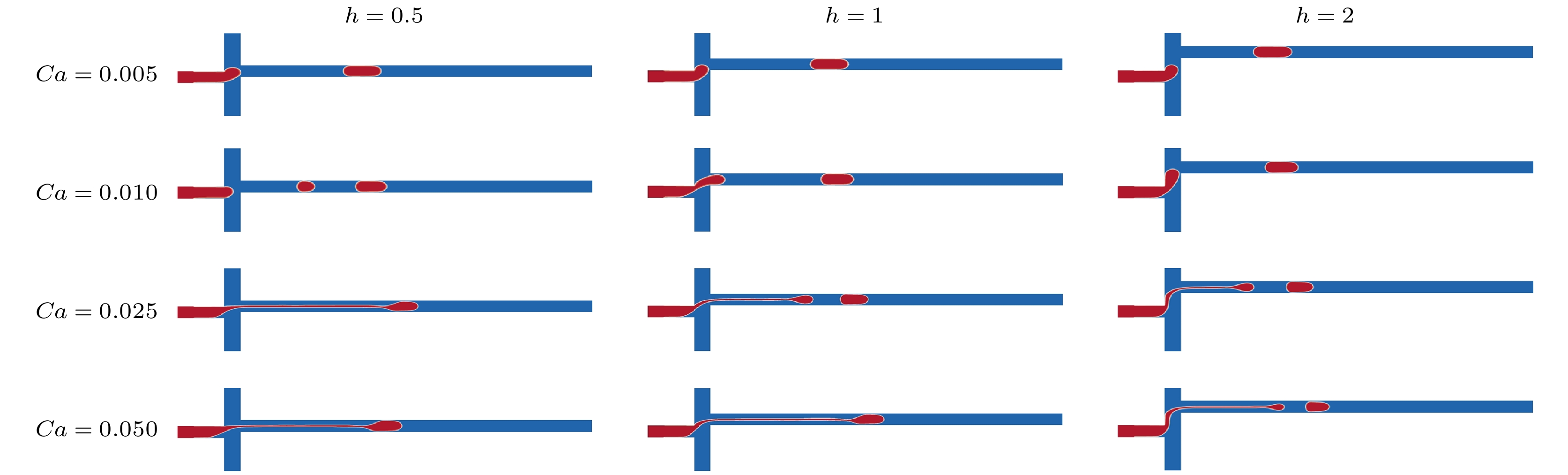
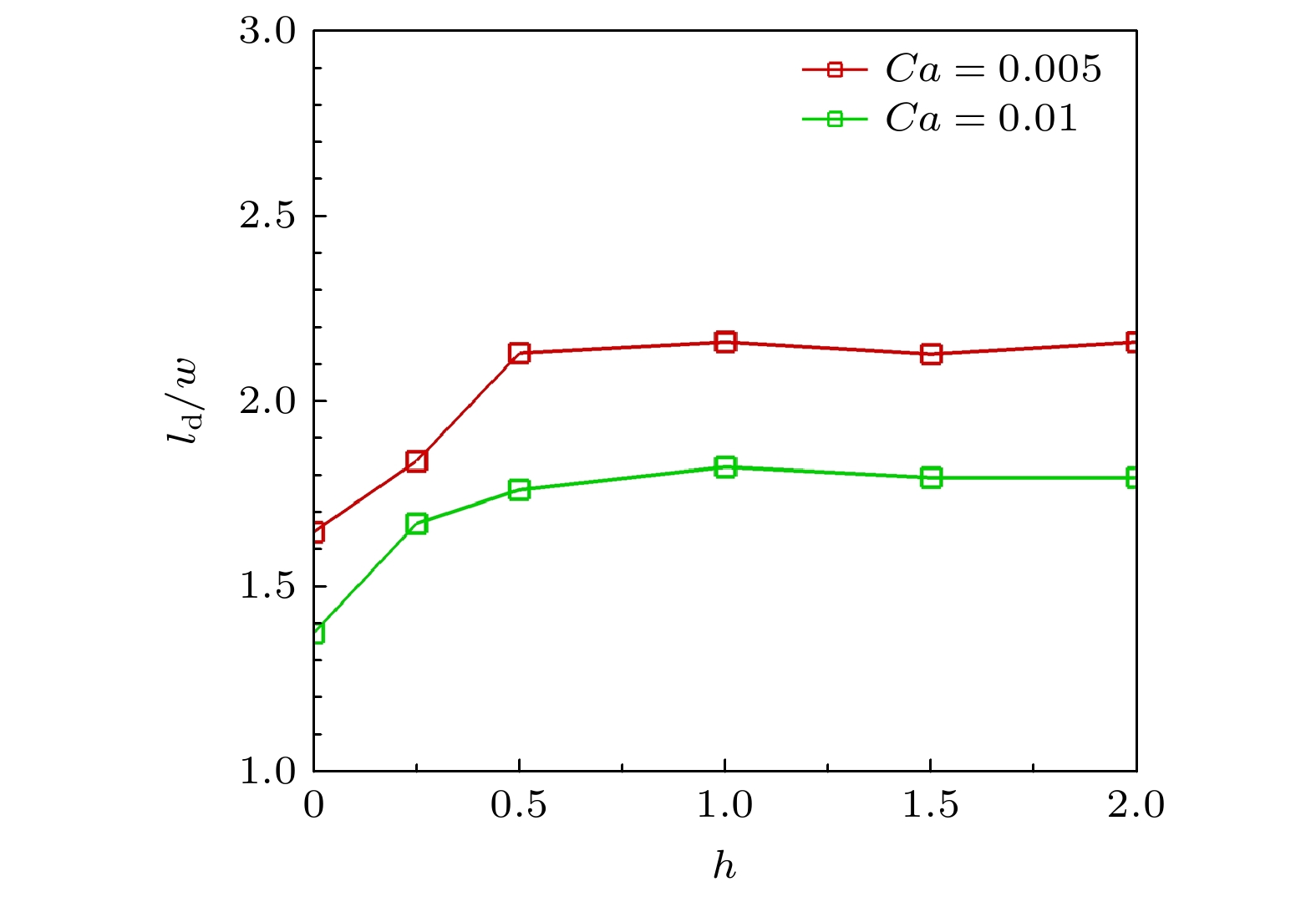
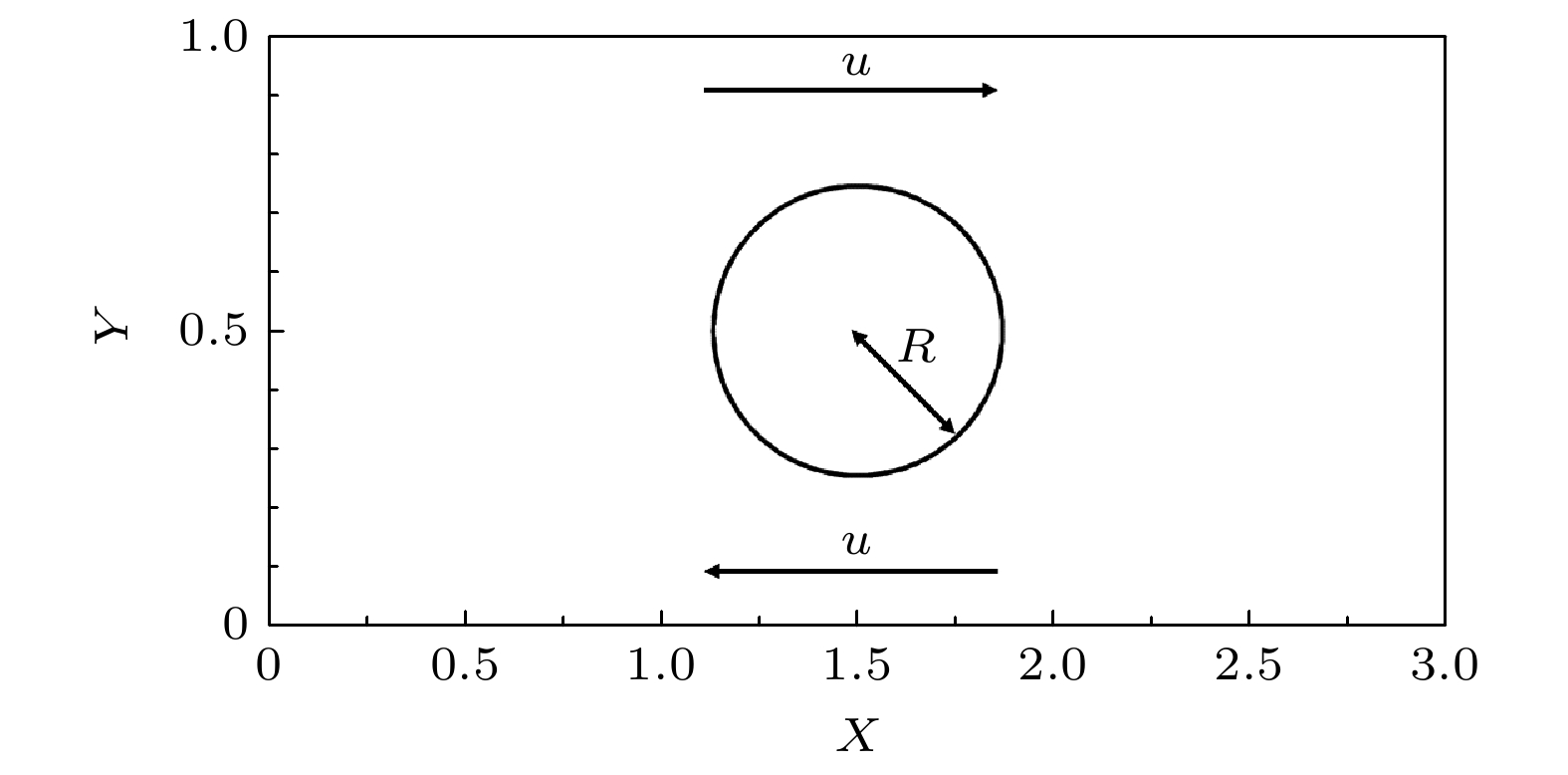
Droplet microfluidics technology presents significant potential for applications in chemical analysis, biological detection, and material preparation. Passive droplet generation methods can rapidly achieve droplet formation by relying on the geometric characteristics of microchannels and shear flow. As a typical structure, the influence of fluid parameters and symmetry differences in cross microchannels on the droplet generation process has not been fully studied. Therefore, this paper uses the lattice Boltzmann method to conduct numerical simulation studies on droplet generation in symmetric and asymmetric cross microchannels, systematically analyzing the action mechanisms of capillary number, viscosity ratio, and microchannel symmetry. First, this study verifies the computational reliability of the numerical model through two classic cases, i.e., the droplet deformation under planar shear flow and stationary droplets on ideal solid surfaces. Then, this work focuses on the three flow stages in symmetric cross microchannels, i.e., the interface immersion stage, the shear-induced breakup stage, and the droplet migration and coalescence stage, analyzing the collaborative mechanism of capillary number and viscosity ratio. In the symmetric cross microchannel structure, the capillary number is the main factor determining the droplet size in the cross microchannel. With the increase of the capillary number, the surface tension gradually weakens, causing the liquid bridge at the droplet neck to break more easily and generate droplets. In contrast, the effect of the viscosity ratio on the droplet size is relatively small, but it can suppress the generation of sub-droplets and improve the uniformity of droplets by adjusting the viscous resistance of the continuous phase. On this basis, the study further quantifies the impact of microchannel symmetry on the droplet generation process in cross microchannels. In the asymmetric cross microchannel structure, the microchannel deviation breaks the flow symmetry and weakens the cooperative shearing effect of the oil-phase fluid on the immersion structure of the water-phase fluid. When the microchannel deviates within the centerline range of the water-phase microchannel, the droplet size increases significantly with the increase of the microchannel deviation. This is mainly because the oil-phase fluid on the side far from the deviation first squeezes the immersion structure of the water-phase fluid, and then the oil-phase fluid near the deviation side performs secondary squeezing on the immersion structure, resulting in the continuous elongation of the neck liquid bridge of the immersion structure and the offset of the shear position along the microchannel deviation direction. When the microchannel deviation exceeds the centerline position of the water-phase microchannel, the interface fracture of the water-phase immersion structure mainly relies on the double squeeze effect of the oil-phase fluid and the surface tension of water-phase fluid, and the droplet size tends to be stable. The relevant research results provide a theoretical basis for microchannel design and fluid parameter regulation in droplet microfluidics and further promote the application and development of droplet microfluidic technology.